基于信息层的捷联惯导信号反演技术
王晓君, 韩正阳, 许向阳
(河北科技大学信息科学与工程学院, 石家庄 050054)
捷联惯导系统(strapdown inertial navigation system,SINS)把惯导仪器直接固联在载体上,用计算机来完成导航功能,省去了复杂的物理实体平台,相较于平台式惯导系统具有结构简单、体积小等优点[1]。但这些优点是用复杂的算法设计和繁重的计算负荷换取的。由于高精度的惯导器件实物价格昂贵且建模复杂[2],因此,需要研究惯导信号的反演技术,对载体轨迹反解算从而模拟惯导器件的测量值,以供后续的组合导航及惯导解算方程研究。
中外许多学者对载体轨迹生成进行了全方面的仿真[3],这为研究惯导信号反演算法提供科学依据。惯导反演算法从载体轨迹中提取需要的信息,然后进行推算得出惯性传感器的测量值。文献[4]研究了组合导航仿真轨迹发生器;文献[5]使用飞行器六自由度模型生成捷联惯导轨迹发生器,使惯导系统和飞控有机地融合到一起;文献[6]仿真出了无人机机动过程和轨迹参数的获取。
主要基于信息层的捷联惯导系统的仿真,介绍如何将载体轨迹中的位置、速度等数据信息反演得到惯导器件测量值: 比力、角速度,并做误差分析验证了反演算法的准确性,该算法避免了复杂的惯导器件物理建模,提高后续对捷联惯导系统的研究效率,也为组合导航中惯导参数传递的实时性要求提供了新的研究方向。
1 仿真结构设计
基于信息层的捷联惯导信号反演仿真系统原理图如图1所示,包括信号反演单元、接收机单元和误差分析单元。
为了验证反演过程的准确性,构建一套半实物仿真系统,分为信号反演、接收机和误差分析3个单元。信号反演单元为系统工作的关键,以无人机为例建立运动学模型[7],将预设轨迹中的运动参数进行反演,包括时间、位置、速度和欧拉角,并以信息帧的格式输出反演结果:比力和角速度。接收机单元和误差分析单元负责对反演的结果进行验证,将比力和角速度作为惯导器件测量值对其进行定位解算,得到的位置和速度结果再与预设值对比,分析误差。
整个仿真系统验证了信号反演过程的准确性,该过程不需要再对惯导器件进行物理建模,避免了烦琐复杂的建模分析过程,并且在信息层面上进行数据结构的反演便可得到惯导器件测量值,大大提高了运算速度,应用到无人机上其处理速度可以达到与飞行控制系统实时交互。此系统对于惯性导航接收机、组合导航接收机、组合导航欺骗干扰等领域具有较好的参考和应用价值。

图1 捷联惯导信号反演仿真系统原理图Fig.1 Schematic diagram of sins signal inversion simulation system
2 捷联惯导信号反演
惯导信号反演算法可视为惯性导航方程参数更新的逆过程,载体运动过程中位置、速度以及姿态数据生成的方法,生成基于一定数据格式的载体运动参数后,需要对其运动轨迹进行反解算,模拟惯性器件在此轨迹下的陀螺仪和加速度计输出,得到比力、角速度结果为信息帧格式,可再用于组合导航之间的参数传递,避免了正向的建模过程,从而大大简化了仿真程序,并且帧格式的数据结构加快了整体的仿真速度,实现了减少仿真数据量、提高研究效率的重要意义。
信号反演原理如图2所示,惯导反演单元共分为三个部分,首先进行的是由预设轨迹计算姿态矩阵,然后是从姿态更新过程中完成比力、角速度的反演部分,最后是零偏误差、比例因子和交叉耦合误差等误差项的建模部分。
2.1 坐标系定义
在惯性导航中,通常需要先指定坐标系才能根据具体的坐标系完成运动载体的导航解算,大部分导航参数也需要在不同坐标系之间进行转换才能使用。为了分析和讨论方便,首先定义4个常用坐标系[8]。
2.1.1 惯性坐标系(i系)
如图3所示,原点位于地球质心,zi轴沿地球自转轴,xi轴指向春分点,yi轴与xi轴、zi轴一起构成右手直角坐标系。
2.1.2 地球坐标系(e系)

图2 信号反演原理图Fig.2 Signal inversion schematic diagram
如图4所示,与i系类似,原点位于地球质心,ze轴沿地球自转轴指向北极点,xe轴由地心指向赤道与本初子午线的交点,ye轴垂直于xOz平面。
2.1.3 载体坐标系(b系)
如图5所示,原点位于载体重心,通常定义xb轴为载体正常运动前向,zb轴为地向(即向下方向),yb轴为右向,三轴构成正交坐标系。
2.1.4 导航坐标系(n系)
如图6所示,原点位于载体质心,通常定义zn轴指向地心方向,xn轴指向北极,由此得到的正交系的yn轴指向东向,故又称北东地坐标系。
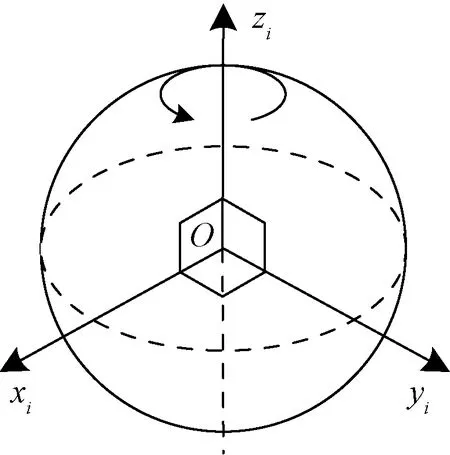
图3 惯性坐标系原点和坐标轴Fig.3 Inertial coordinate system origin and axis

图4 地球坐标系原点和坐标轴Fig.4 Earth coordinate system origin and axis

图5 载体坐标系原点和坐标轴Fig.5 Carrier coordinate system origin and axis
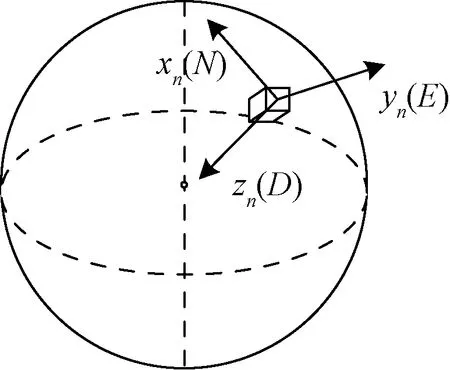
图6 导航坐标系原点和坐标轴Fig.6 Navigation coordinate system origin and axis
2.2 姿态矩阵的计算
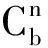

(1)
2.3 信号反演算法
由于在导航系统中地球坐标系(e系)通常用作相对参考以及投影坐标系,研究时比较便利,因而确定在地球坐标系(e系)下表示导航结果。

(1)位置rx、ry、rz转化关系式为

(2)
式(2)中:RE为卯酉圈曲率半径;L、λ、h分别为纬度、经度、高度;e′为地球第一偏心率。
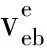

(3)
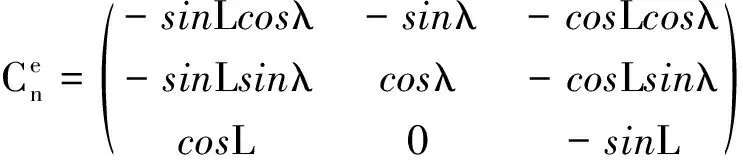
(4)
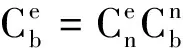
(5)
在将各个导航参数转换到地球坐标系(e系)下的基础上,可进行惯导的反演解算,实现对惯导器件输出值,即比力、角速度的求解。反演算法可视为SINS导航参数更新的逆过程。
2.3.1 比力反演
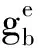

(6)

(7)
由于比力测量值通常是在加速度计三轴体坐标系内表示的,所以将其坐标转换一次得
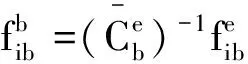
(8)
2.3.2 角速度反演

(9)
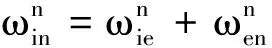
(10)
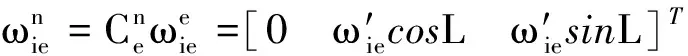
(11)

(12)
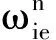
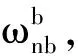

(13)
为了提高惯性器件的信息求解精度,可适当地减小解算的步长,再将相邻数次轨迹点的信息增量累加,当作一次采样输出。
2.4 误差建模
反演计算得到的比力和角速度为理想条件下的测量值,但各种加速度计和陀螺仪常伴随着各种误差特性,导致在仿真过程中为了模拟真实的运动情况,还需要在仿真数据上添加误差项,最终真实地模拟惯导器件输出比力、角速度。
惯性仪表误差主要包含确定性误差和随机性误差。确定性误差有零偏误差、比例因子和交叉耦合误差等固有误差,主要受传感器振动和制作工艺所限,实际中确定误差会随着载体运动时间长短、传感器设计方式不同而变化[10]。随机性误差主要由随机噪声和量化过程产生,通常用功率谱密度方根和量化电平来表示[11]。
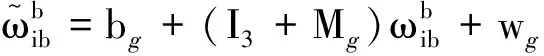
(14)
式(14)中:bg为陀螺仪的零偏误差;I3为单位矩阵;Mg为陀螺仪比例因子和交叉耦合误差;wg为陀螺仪随机量化电平。
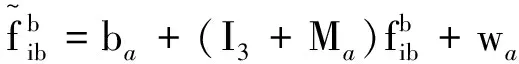
(15)
式(15)中:ba为加速度计的零偏误差;I3为单位矩阵;Ma为加速度计比例因子和交叉耦合误差;wa为加速度计随机量化电平。
叠加误差后的反演数据更能真实地反映惯导系统的工作情况,接下来则需要验证反演算法的准确性。
3 仿真验证与分析
先假定位置、速度和欧拉角的真值,反演计算出比力和角速度,然后利用惯导定位方程进行位置和速度的解算,与初始设定的位置和速度进行对比来验证反演过程的准确性。
由一段连续的三维运动轨迹推导生成10 000个时刻的反演数据,设置惯导器件的误差参数并将各项误差进行归一化处理,如加速度计零偏误差为0.017 4 m/s2,陀螺仪零偏误差8.59×10-5rad/s等。用10 000个时刻的反演数据进行惯导解算后,得到了如图7、图8所示的结果。其中,图7中黑色直线表示原始目标在地球坐标系下的轨迹,而红色折线代表反演数据定位得到的轨迹,可以看出定位结果与原始目标的运动轨迹基本吻合,而每个时刻点的距离误差如图8所示。

图7 运动轨迹及定位结果对比Fig.7 Comparison of motion track and positioning result chart
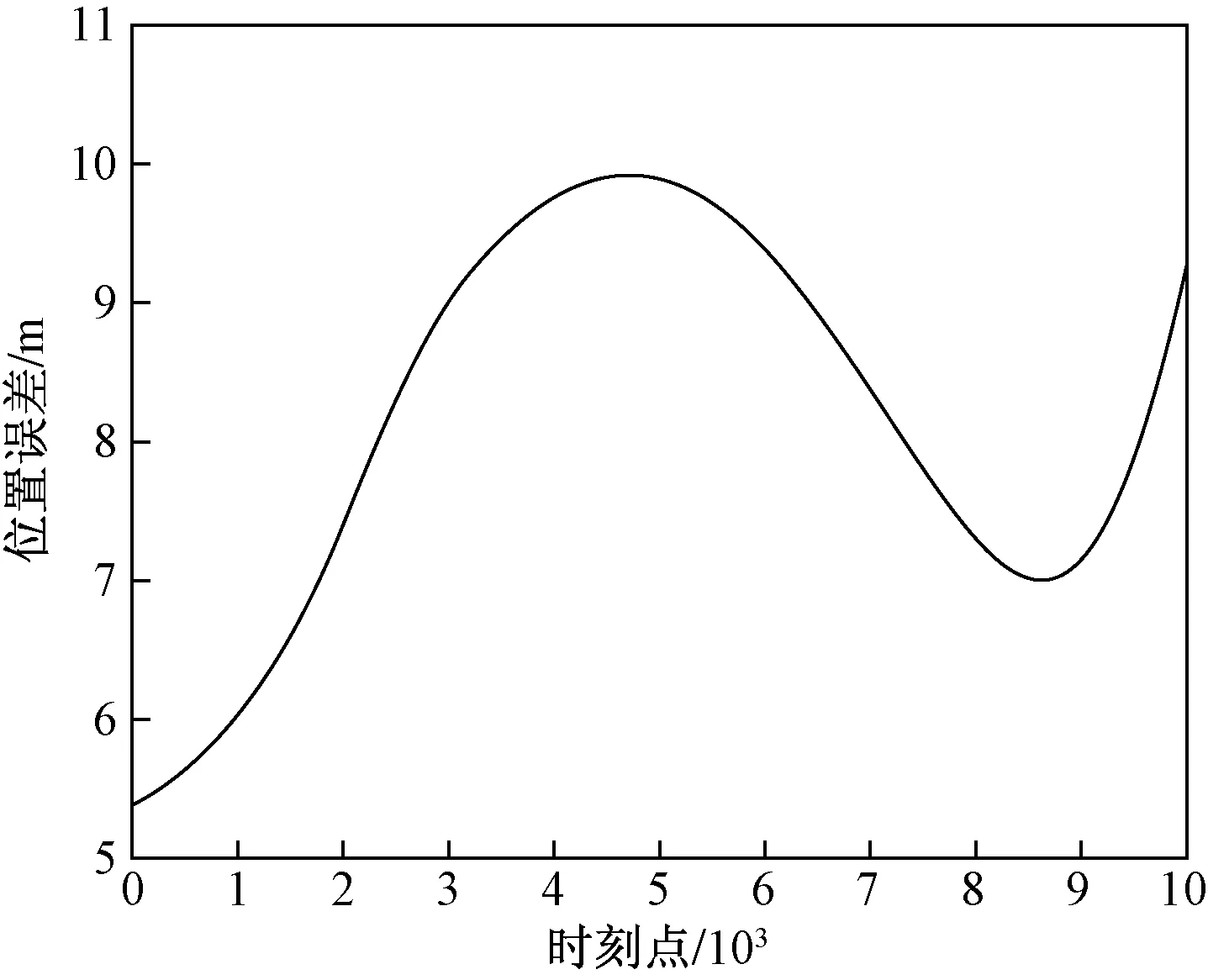
图8 定位结果误差Fig.8 Error of positioning results
图9、图10为速度的反演结果。其中图9的黑色直线代表原始目标在北、东、地方向上的速度,而红色直线代表反演数据得到的速度结果,可以看出定速结果也与原始目标的速度高度拟合。图10则记录了各个方向(北向、东向、地向)上的具体速度误差。

图9 北、东、地方向速度及定速结果对比Fig.9 Comparison of north, east and down speed and constant speed result chart
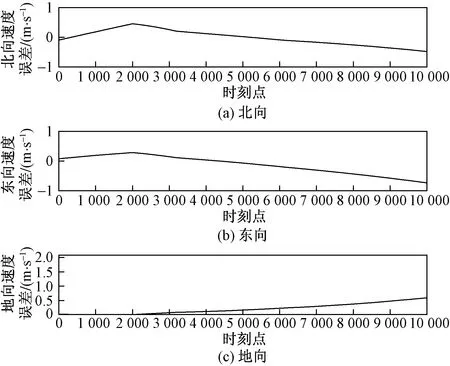
图10 北、东、地方向速度误差Fig.10 North, east and down velocity error
4 结论
针对惯导器件价格昂贵不适合在开发过程中随意使用调试,而建模时物理结构又非常复杂的问题,提出了一种基于信息层的捷联惯导信号反演技术,可模拟生成实时的惯导器件测量数据,根据预设的运动目标轨迹,反演推出不同时刻惯导器件的输出值,避开了对惯导器件的建模过程,大大提高了仿真系统的运行速度。采用信息层的半实物仿真系统,用信息帧表征惯导信号输出,不涉及惯导器件中的物理结构,其处理速度可以达到与飞行控制系统实时交互的程度,未来可用于无人机等飞行器的组合导航性能测试和捷联惯导算法验证。由于不同级别的惯性传感器精度并无统一界定,但可以确定惯导精度的限制会影响最终测量结果,在反演过程中使用的各项参数属于仿真环境下的理想值,导致反演结果会与实际惯导器件的测量值有可接受范围内的出入。仿真结果显示,将反演出的比力和角速度再次进行定位,结果可正确收敛于原始目标位置和速度,也验证了反演算法在仿真环境中的准确性。

