基于新颖S型转换函数的二进制粒子群优化算法求解具有单连续变量的背包问题
王泽昆,贺毅朝,李焕哲,张发展
(河北地质大学信息工程学院,石家庄 050031)
(*通信作者电子邮箱heyichao@hgu.edu.cn)
0 引言
粒子群优化(Particle Swarm Optimization,PSO)[1]是1995年由Kennedy和Eberhart 提出的一种著名演化算法,具有结构简单、易于实现和计算成本低等优点,受到众多学者的关注和研究,已经在神经网络[2]、约束优化[3]、调度问题[4]等众多问题中得到了成功应用。为了利用PSO 求解二元优化问题,Kennedy 和Eberhart[5]随后提出了二进制粒子群优化(Binary Particle Swarm Optimization,BPSO)算法。在BPSO 中,利用Sigmoid 转换函数将由实向量表示的粒子速度转换为由0-1向量表示的粒子位置,从而基于粒子速度实现对粒子位置的更新,其中的Sigmoid 转换函数是BPSO 设计与实现的关键所在[6]。
具有单连续变量的背包问题(Knapsack Problem with a single Continuous variable,KPC)[7]是1999 年 由Marchand 和Wolsey 提出的一个带有连续变量S的组合优化问题。目前,国内外学者对KPC的求解算法进行了研究,例如Lin等[8]首先将KPC 转化为一个伪背包问题和标准0-1 背包问题的组合形式,然后分别利用动态规划算法和分支定界法进行求解。贺毅朝等[9]首先利用放缩法将KPC 中的连续变量离散化,将它转化为带有实函数的变载重背包问题的一个特例,然后基于动态规划法提出了一个精确算法DP-KPC。贺毅朝等[10]将KPC 分解为两个具有标准0-1 背包问题形式的子问题进行求解,提出了一个时间复杂度为O(n2)的2-近似算法。最近,He等[11]提出了基于演化算法求解KPC 的新思路,首先基于降维法建立了KPC 的一个适于串行计算的数学模型和一个适用于并行求解的数学模型,然后基于混合编码二进制差分演化(Binary Differential Evolution with Hybrid encoding,HBDE)算法[12]给出了求解KPC 的两个高效离散演化算法:具有混合编码的单种群二进制差分演化(Single-population Binary Differential Evolution with Hybrid encoding,S-HBDE)算法和具有混合编码的双种群二进制差分演化(Bi-population Binary Differential Evolution with Hybrid encoding,B-HBDE)算法。显然,求解KPC 的已有算法分为两类:精确算法和非精确算法。精确算法[8-9]具有伪多项式时间复杂度,不适用于求解大规模KPC 实例;而非精确算法[10-11]特别是演化算法不仅求解KPC的速度快,而且计算结果完全能够满足实际应用要求。因此探讨利用演化算法求解KPC 的高效方法是一个值得研究与探讨的问题。
本文在已有转换函数的基础上,通过进一步的变形,提出了一个新颖S 型转换函数,并基于这一转换函数给出了一个新颖的二进制粒子群优化(New Binary Particle Swarm Optimization,NBPSO)算法。为了验证NBPSO算法的性能,通过与基于已有4 个S 型转换函数和4 个V 型转换函数的各种二进制PSO(分别记为S1-BPSO、S2-BPSO、S3-BPSO、S4-BPSO、V1-BPSO、V2-BPSO、V3-BPSO 和V4-BPSO)、具有双重结构编码的二进制粒子群优化(Binary Particle Swarm Optimization with Double Structure coding,DS-BPSO)算法[13]以及文献[11]中的算法S-HBDE、B-HBDE和BPSO求解4类KPC实例[11]的计算结果进行比较,结果显示NBPSO 在求解KPC 时明显优于对比算法。
1 KPC定义与数学模型
KPC 的定义为:给定n个物品的集合N={1,2,…,n}和一个基本载重为C的背包,其中物品j∈N具有价值pj和重量wj,背包的可变载重S∈[l,u],pj、wj和C为正有理数,S、l和u为有理数,且l<0 <u;给定一个系数c>0 作为惩罚系数。如果可变载重S>0,即背包容量加S,则总价值将减去cS;反之,如果可变载重S<0,即背包容量减|S|,则总价值加|cS|。KPC 目标是确定S的取值,使得装入物品的重量之和在不超过背包载重C+S的前提下的价值之和减去cS最大。
根据上述定义,KPC 的基本数学模型KPCM1[11]描述如下:

其中:Y=[y1,y2,…,yn]∈{0,1}n,yj=1(j=1,2,…,n) 表 示物品j被装入了背包中。为了便于利用二进制演化算法求解KPC,文献[11]基于降维法建立了KPC 的一个新数学模型KPCM2,该模型通过消去连续变量S使解空间的维数由n+1降低为n。数学模型KPCM2的描述如下:

显然模型KPCM2 中不涉及可变载重S。因此,本文利用演化算法基于模型KPCM2 求解KPC 时,可适当降低求解的难度。
2 BPSO与NBPSO
2.1 BPSO
PSO 算法是模拟鸟群飞行觅食的行为,通过个体之间的协作来寻找最优解的进化计算技术。该算法包含粒子的速度更新(式(7))和位置更新(式(8))两个重要操作:

在BPSO 中,Kennedy 和Eberhart[5]首先引入了Sigmoid 函数(即式(9)),然后再利用式(10)替换PSO中的粒子位置更新操作(即式(8)),使得的值只取0或1。
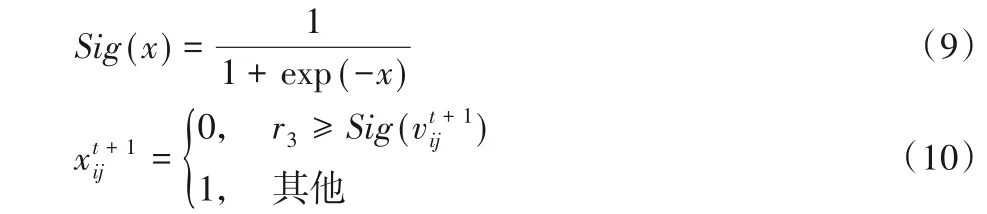
其中,r3为0~1的随机数。在式(10)中,利用Sigmoid 函数将粒子速度转换为概率值,根据转换后的概率值和r3之间的关系来更新粒子的位置。
2.2 NBPSO
2.2.1 一个新的S型转换函数
近年来,转换函数成为二进制演化算法研究的一个热点,各种的新的转换函数应运而生。值得一提的是,Mirjalili 等[6]在已有两个转换函数的基础上,提出了6 个新的转换函数,大大丰富了二进制演化算法的设计方法。目前,已有的转换函数分为两种:S 型转换函数和V 型转换函数[6,14],下面给出了8个常用的S 型和V 型转换函数(分别记为S1、S2、S3、S4、V1、V2、V3和V4)。


虽然S 型和V 型转换函数的函数值均在[0,1]中,且表示一个概率值,但是S 型和V 型转换函数明显具有不同的特点。为了兼具S 型和V 型转换函数的特性,本文基于V 型转换函数中的函数V1提出一个新的S型转换函数NS如下:

实际计算表明(请参考表1~4):基于S2、S3、S4、V1、V3 等转换函数的BPSO 求解KPC 的效果较差,为此下面不再考虑这些转换函数。为了直观地观察NS、S1、V2和V4等转换函数的变化情况,在图1中给出了这四个转换函数的图像。

图1 S1、V2、NS和V4转换函数Fig.1 Transfer functions S1,V2,NS and V4
2.2.2 NBPSO
Lee 等[15]对BPSO 进行了改进,在保持PSO 的速度更新公式和位置更新公式的基础上,利用位置值的概率对粒子的位置进行第二次更新操作。基于这一方法,并结合所给出的新S 型转换函数NS,本文提出了一个新的二进制粒子群优化算法NBPSO。在NBPSO 的进化过程中,首先利用式(7)更新粒子的速度,接着利用式(8)对粒子位置进行第一次更新。然后,利用第一次位置更新后的位置值根据式(20)来计算粒子位置向量变化的概率值。

最后,根据求得的粒子位置向量变化的概率值,利用式(21)对粒子进行第二次位置更新。

根据以上描述,容易给出NBPSO的实现步骤如下:
步骤1 初始化参数。设置最大迭代次数MIter,种群规模N,惯性参数W,加速系数c1、c2和vmax;令t←0。
步骤2 随机初始化种群。使粒子位置的每一分量随机取0 或1,粒子速度的每一分量在[-vmax,vmax]内随机取值。计算种群中所有个体的适应度。
步骤3 分别利用式(7)和式(8)更新每个粒子的速度和位置。
步骤4 利用式(20)计算每个粒子的位置向量的概率,利用式(21)二次更新粒子的位置向量。
步骤5 计算更新后每个粒子的适应度。
步骤6 判断是否满足终止条件。若不满足,则t←t+1,转步骤3;若满足,则输出全局最好位置对应的解以及它的目标函数值。
设O(f)表示计算个体适应的时间复杂度。其中步骤2的时间复杂度为O(N*n) +N*O(f),步骤3~5 的时间复杂度为MIter*(N*(O(n) +O(f) +O(n)) +N*O(n))。当N、MIter和O(f)是关于n的多项式时,NBPSO 是一个具有多项式时间复杂度的随机近似算法。
3 利用NBPSO求解KPC
在利用演化算法求解KPC 时,不可避免地将会产生不可行解。为了解决这一问题,贺毅朝等[11]给出了一种时间复杂度为O(n2)的修复与优化算法M2-GROA 来处理KPC 的不可行解。由于M2-GROA在文献[11]中的成功应用,因此本文利用M2-GROA处理NBPSO在求解KPC时所产生的不可行解。
设Yb∈[0,1]n表示求得KPC 实例的当前最优解,f(Yb)表示Yb所对应的适应度值。基于NBPSO 求解KPC 的算法的步骤如下:
步骤1 将n个物品项利用Quicksort[16]按照物品的价值密度比降序排序,并将排序后的物品项的下标依次存入一维数组H[1,2,…,n]中。
步骤2 初始化参数。设置最大迭代次数MIter,种群规模N,惯性参数W,加速系数c1、c2和vmax;令t←0。
步骤3 随机初始化种群。使粒子位置的每一分量随机取0或1,粒子速度的每一分量在[-vmax,vmax]内随机取值。
步骤4 利用M2-GROA 处理初始化时产生的不可行解,并计算粒子的适应度值。
步骤5 对于所有粒子,分别利用式(7)和式(8)更新它的速度和位置。
步骤6 利用式(20)计算改变粒子位置向量的概率。
步骤7 利用式(21)中二次更新粒子的位置向量。
步骤8 利用M2-GROA 处理粒子更新后所产生的不可行解,并计算它的适应度值。
步骤9 判断是否满足终止条件。若不满足,则t←t+1,转步骤5;若满足,则输出(Yb,f(Yb))。
在上述步骤中,步骤1利用快速排序QuickSort[16]实现,时间复杂度为O(nlogn);步骤3 的时间复杂度为O(N*n);步骤4的时间复杂度为O(N*n2);步骤4~9 的时间复杂度为O(MIter*N*n2);因此NBPSO 求解KPC 的时间复杂度为O(nlogn) +O(N*n) +O(N*n2)+O(MIter*N*n2),其中MIter和N是关于n的多项式,故为多项式时间复杂度。
4 计算结果与分析
所有计算均在配置为Inter Core i7-3770 CPU@3.40 GHz和8 GB RAM 的微型计算机上进行;用C 语言进行编程,编译环 境 为Code:Blocks;使 用Python 在 编 译 环 境JetBrains PyCharm下绘制折线图。
4.1 四类KPC实例
四 类KPC 实 例[11]分 别 为:ukpc 类,编 号 为ukpc100~ukpc1000;ikpc 类,编号为ikpc100~ikpc1000;wkpc 类,编号为wkpc100~wkpc1000;skpc 类,编号为skpc100~skpc1000。所有KPC 实例的数据都来自https://www.researchgate.net/project/KPC-problem-and-Its-algorithms。
4.2 计算结果比较与分析
由于基于S2、S3、S4、V1、V3 五个转换函数的二进制PSO和DS-BPSO[13]求解KPC 的效果极差(请参考表1~4),因此,只对 算 法NBPSO、S1-BPSO、V2-BPSO、V4-BPSO、S-HBDE、B-HBDE和BPSO进行实验比较分析。
在NBPSO、S1-BPSO、V2-BPSO 和V4-BPSO 中,各算法的种群规模均为N=20,最大迭代次数均为MIter=6*n,n为KPC 实例中物品的个数;此外,惯性参数W=1.5,加速系数c1=c2=1.8,粒子速度向量中各维分量的取值范围为[-2,2]。S-HBDE、B-HBDE 和BPSO 的种群规模均为N=20,三算法其他参数与文献[11]中相同。
记OPT是利用文献[9]中方法求得KPC 实例的最优值;Best为算法独立计算实例50 次所得计算结果中的最好值;Mean和StD分别为50 次所得计算结果的平均值和标准差;AR=|OPT-Mean|表示各算法求解KPC 实例的计算结果的平均值与最优值之间的绝对误差。在表5~8中给出了各算法求解四类KPC 实例的计算结果,并根据表5~8 中的计算结果比较NBPSO、S1-BPSO、V2-BPSO、V4-BPSO、S-HBDE、B-HBDE和BPSO等七个算法计算结果的优劣。
记Bnum表 示NBPSO、S1-BPSO、V2-BPSO、V4-BPSO、S-HBDE、B-HBDE 和BPSO 的Best值达到OPT值的实例个数,Mnum表示NBPSO、S1-BPSO、V2-BPSO、V4-BPSO、S-HBDE、B-HBDE和BPSO的Mean值达到OPT值的实例个数,在表9对各算法的这两个指标进行了比较。
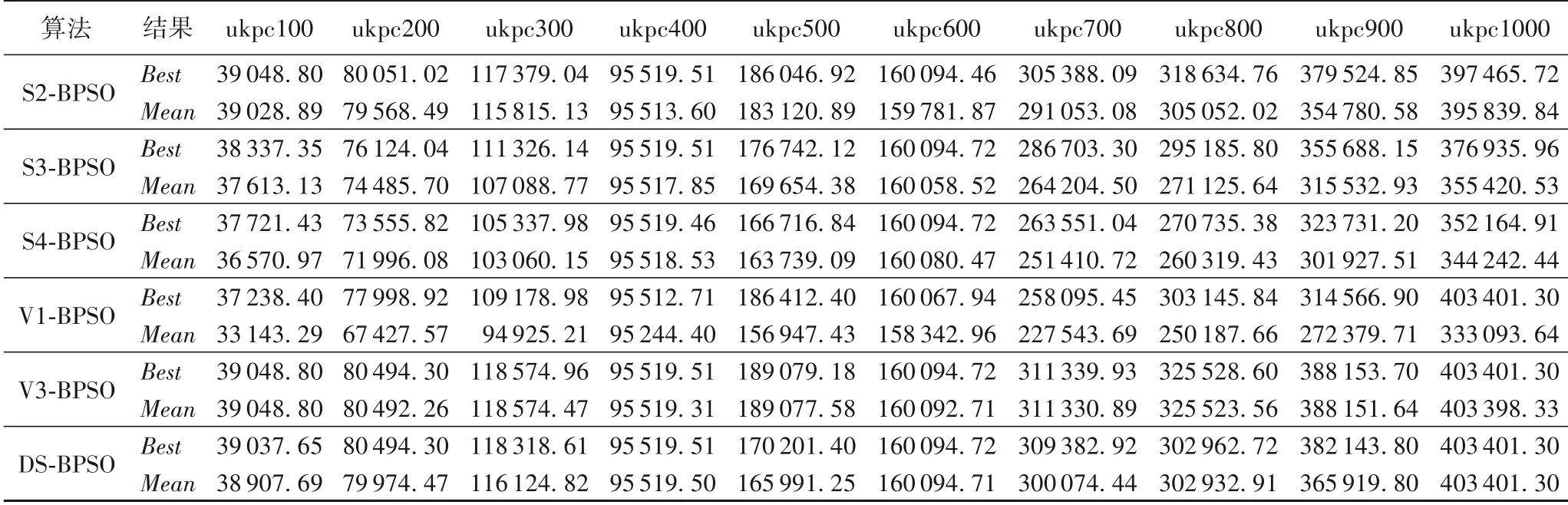
表1 S2-BPSO、S3-BPSO、S4-BPSO、V1-BPSO、V3-BPSO和DS-BPSO求解ukpc类实例的计算结果Tab.1 S2-BPSO,S3-BPSO,S4-BPSO,V1-BPSO,V3-BPSO and DS-BPSO calculation results of ukpc class instances
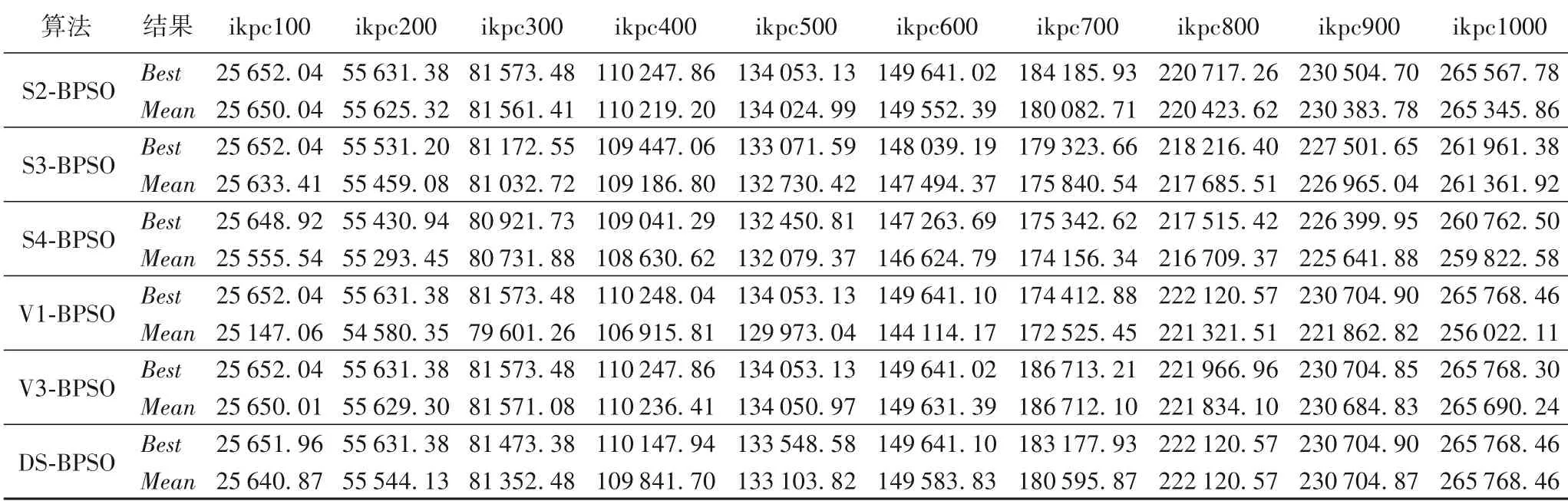
表2 S2-BPSO、S3-BPSO、S4-BPSO、V1-BPSO、V3-BPSO和DS-BPSO求解ikpc类实例的计算结果Tab.2 S2-BPSO,S3-BPSO,S4-BPSO,V1-BPSO,V3-BPSO and DS-BPSO calculation results of ikpc class instances

表3 S2-BPSO、S3-BPSO、S4-BPSO、V1-BPSO、V3-BPSO和DS-BPSO求解wkpc类实例的计算结果Tab.3 S2-BPSO,S3-BPSO,S4-BPSO,V1-BPSO,V3-BPSO and DS-BPSO calculation results of wkpc class instances
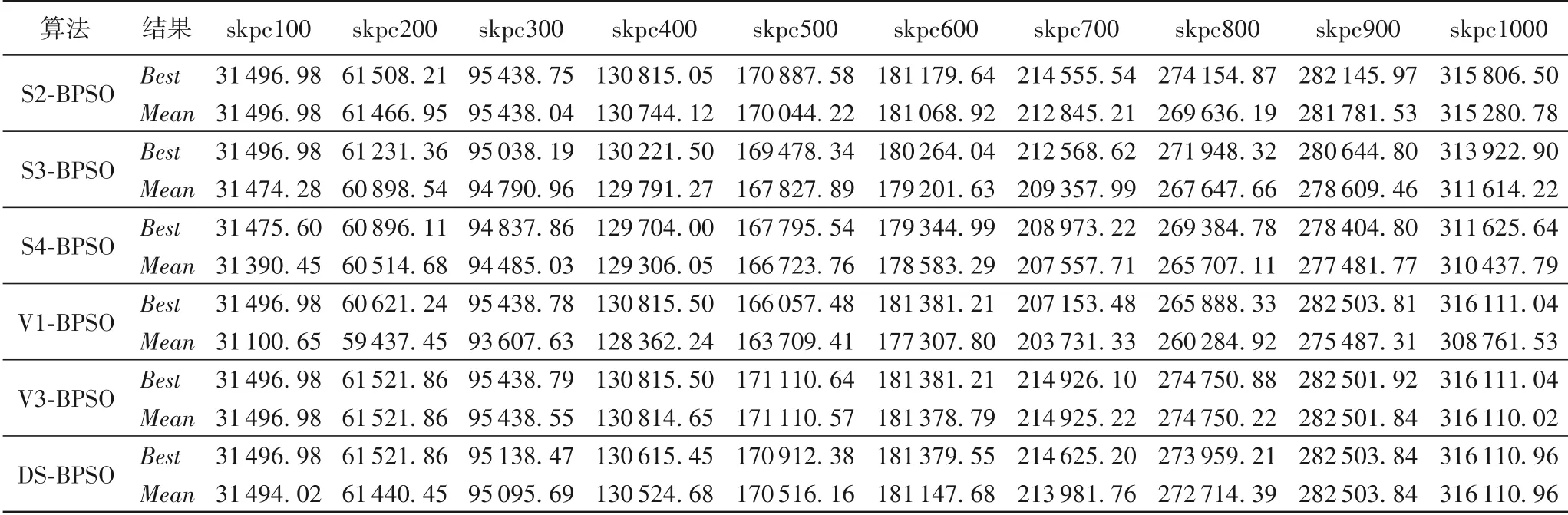
表4 S2-BPSO、S3-BPSO、S4-BPSO、V1-BPSO、V3-BPSO和DS-BPSO求解skpc类实例的计算结果Tab.4 S2-BPSO,S3-BPSO,S4-BPSO,V1-BPSO,V3-BPSO and DS-BPSO calculation results of skpc class instances
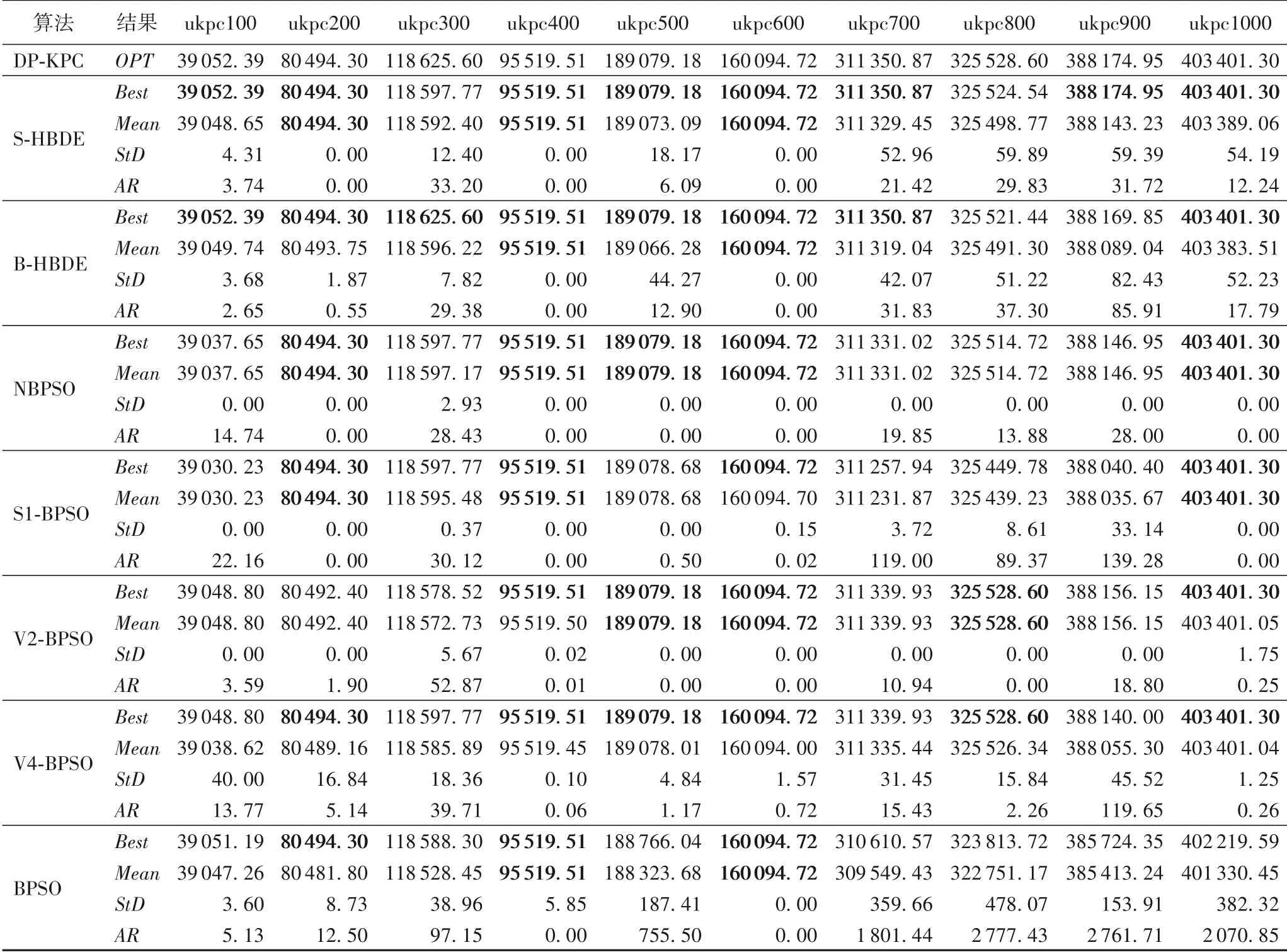
表5 S-HBDE、B-HBDE、NBPSO、S1-BPSO、V2-BPSO、V4-BPSO和BPSO求解ukpc类实例的计算结果Tab.5 S-HBDE,B-HBDE,NBPSO,S1-BPSO,V2-BPSO,V4-BPSO and BPSO calculation results of ukpc class instances

续表

表7 S-HBDE、B-HBDE、NBPSO、S1-BPSO、V2-BPSO、V4-BPSO和BPSO求解wkpc类实例的计算结果Tab.7 S-HBDE,B-HBDE,NBPSO,S1-BPSO,V2-BPSO,V4-BPSO and BPSO calculation results in solving wkpc class instances
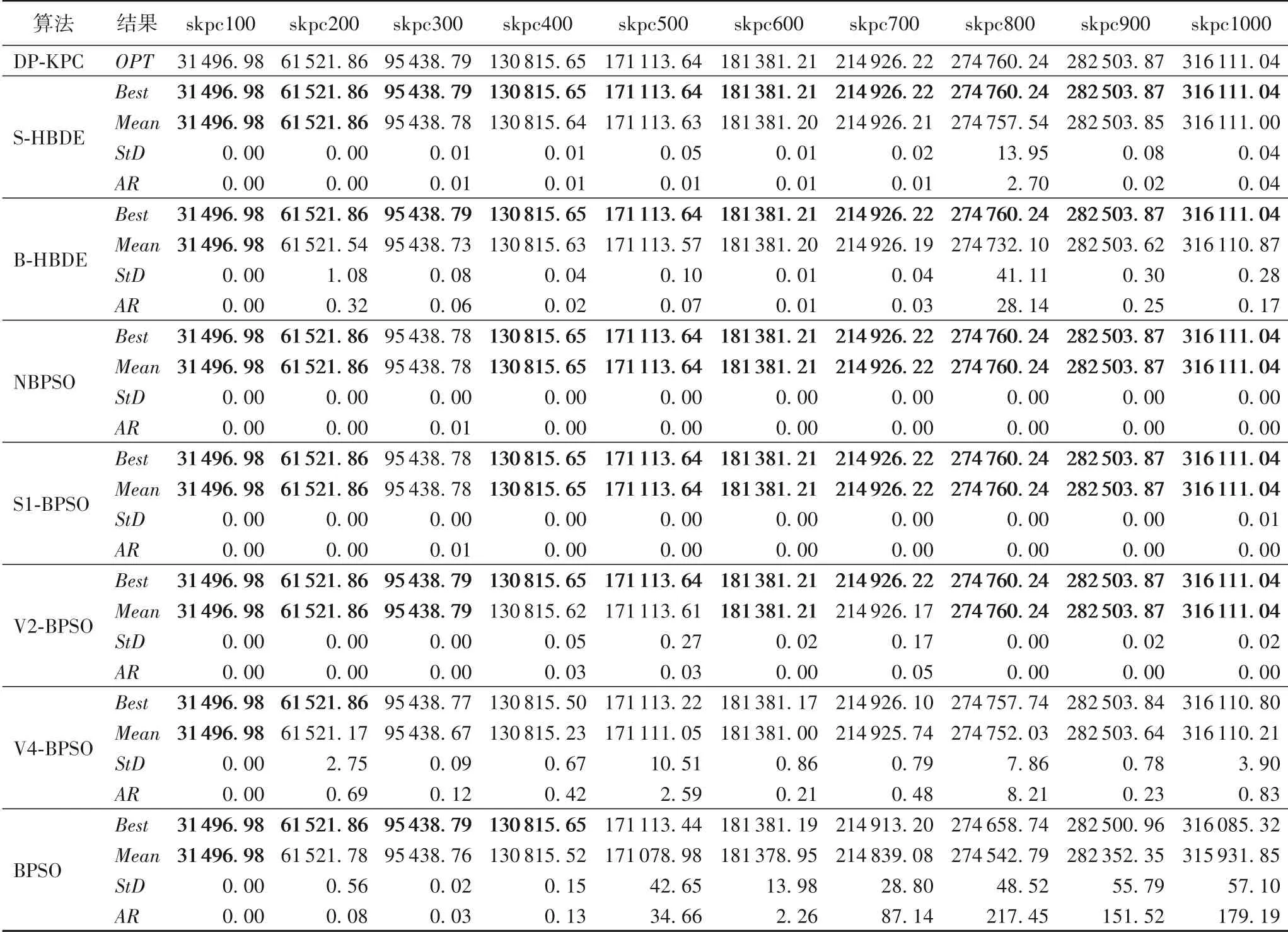
表8 S-HBDE、B-HBDE、NBPSO、S1-BPSO、V2-BPSO、V4-BPSO和BPSO求解skpc类实例的计算结果Tab.8 S-HBDE,B-HBDE,NBPSO,S1-BPSO,V2-BPSO,V4-BPSO and BPSO calculation results in solving skpc class instances

表9 各算法比较分析Tab 9 Comparison and analysis of various algorithms
由表5~8和表9可以看出,对于40个KPC 实例,从算法的Best和Mean来看,NBPSO、S1-BPSO和V2-BPSO均有一半以上实例的Best值达到OPT值,V4-BPSO 相较于NBPSO、S1-BPSO和V4-BPSO 较 差。在40个实例中,NBPSO 有22个实例的Mean值达到OPT值,达到OPT值的实例个数是最多的,其次是S1-BPSO,然后是V2-BPSO,V4-BPSO 的最少。因此,NBPSO 算法明显比S1-BPSO、V2-BPSO 和V4-BPSO 求解KPC的效果更佳。
由表5~8和表9还可看出,NBPSO 与S-HBDE、B-HBDE 和BPSO 相比较,S-HBDE 的Bnum值最大,即在40个KPC实例中Best值达到OPT值的实例最多,求解精度最高,其次是B-HBDE,最后是NBPSO。但从Mnum来看,NBPSO 在保证所有KPC 实例中一半以上实例的Best值达到OPT值的基础上,相较于B-HBDE 将求得Mean值达到OPT值的实例个数提高了4.5 倍;相较于BPSO 将求得Mean值达到OPT值的实例个数提高了约2.7 倍;相较于S-HBDE 将求得Mean值达到OPT值的实例个数提高了约2.1 倍。由于在评价演化算法时,指标Mean比指标Best更能说明问题演化算法的性能优劣,因此NBPSO比S-HBDE、B-HBDE和BPSO求解KPC的性能更佳。
为了更直观地比较,在图2~5 中绘制了S-HBDE、B-HBDE、NBPSO、S1-BPSO、V2-BPSO、V4-BPSO 和BPSO 算法的AR拟合曲线,根据AR拟合曲线对它们作进一步比较。
从图2 可以看出,S1-BPSO 在求解实例ukpc100、ukpc700~ukpc900 的结果较差;V2-BPSO 除了求解实例ukpc300 的结果较差外,对其他实例的计算结果较好;V4-BPSO 仅求解实例ukpc400~ukpc600 和ukpc1000 的结果较好,对其他实例的计算结果略差;NBPSO 在求解实例ukpc200~ukpc600 和ukpc1000 的结果较好,大部分实例的计算结果比S-HBDE、B-HBDE和BPSO要好。

图2 求解实例ukpc100~ukpc1000的AR拟合曲线Fig.2 AR fitting curves in solving instances ukpc100-ukpc1000
从图3 不难看出,S1-BPSO 除了求解实例ikpc700 的结果较差外,对于其他实例的计算结果均较好;V2-BPSO除了求解实例ikpc800 的结果较好外,对其他实例的计算结果,与NBPSO、V4-BPSO 相比均较差;NBPSO 和V4-BPSO 求解所有实例的结果相差不大且比其他算法要好;BPSO 相比其他6 个算法表现最差。

图3 求解实例ikpc100~ikpc1000的AR拟合曲线Fig.3 AR fitting curves in solving instances ikpc100-ikpc1000
从图4可以看出,S1-BPSO 求解实例wkpc400、wkpc600和wkpc1000 的结果较差,但对其他实例的计算结果较好;V4-BPSO 仅求解实例wkpc100、wkpc500、wkpc700 和wkpc900 的计算结果较好,对其他实例的计算结果均较差;NBPSO 求解大部分实例的结果比S-HBDE、B-HBDE、S1-BPSO、V2-BPSO、V4-BPSO和BPSO的要好。

图4 求解实例wkpc100~wkpc1000的AR拟合曲线Fig.4 AR fitting curves in solving instances wkpc100-wkpc1000
从图5 不难看出,S-HBDE 和B-HBDE 求解实例skpc800的计算结果较差,但对于其他实例的计算结果较好;V4-BPSO求解实例skpc500 和skpc800 的计算结果较差;NBPSO、S1-BPSO 和V2-BPSO 求解所有实例的结果几乎达到最优值且比其他算法的要好;BPSO相比其他6个算法表现最差。

图5 求解实例skpc100~skpc1000的AR拟合曲线Fig.5 AR fitting curves in solving instances skpc100-skpc1000
通过以上比较可以看出:NBPSO 在求解四类KPC 实例时,虽然部分Best达不到OPT,但是大部分Mean和部分Best相比S-HBDE、B-HBDE 和BPSO 均有所改善,而且明显优于S1-BPSO、V2-BPSO和V4-BPSO等演化算法。
在图6~9 中给出了S-HBDE、B-HBDE、NBPSO、S1-BPSO、V2-BPSO、V4-BPSO 和BPSO 的StD对应的曲图,从中可以看出,对于ukpc、ikpc、wkpc 和skpc 四类实例,NBPSO 的算法稳定性总的来说比S-HBDE、B-HBDE、S1-BPSO、V2-BPSO、V4-BPSO 和BPSO 的要好;虽然对于个别实例,NBPSO 的稳定性比S1-BPSO、V4-BPSO、S-HBDE 和B-HBDE 的要差,但是对于绝大部分其他实例,NBPSO 的稳定性明显要比其他算法的好。
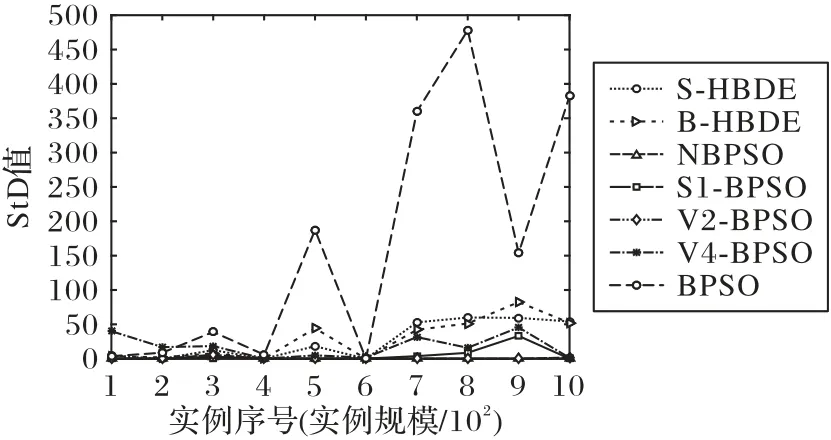
图6 求解实例ukpc100~ukpc1000的StD曲线Fig.6 StD curves in solving instances ukpc100-ukpc1000
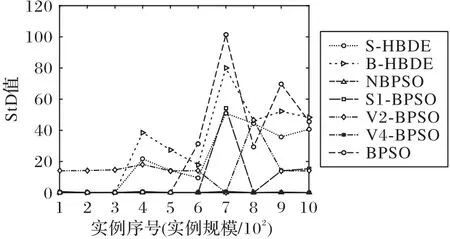
图7 求解实例ikpc100~ikpc1000的StD曲线Fig.7 StD curves in solving instances ikpc100-ikpc1000

图8 求解实例wkpc100~wkpc1000的StD曲线Fig.8 StD curves in solving instances wkpc100-wkpc1000
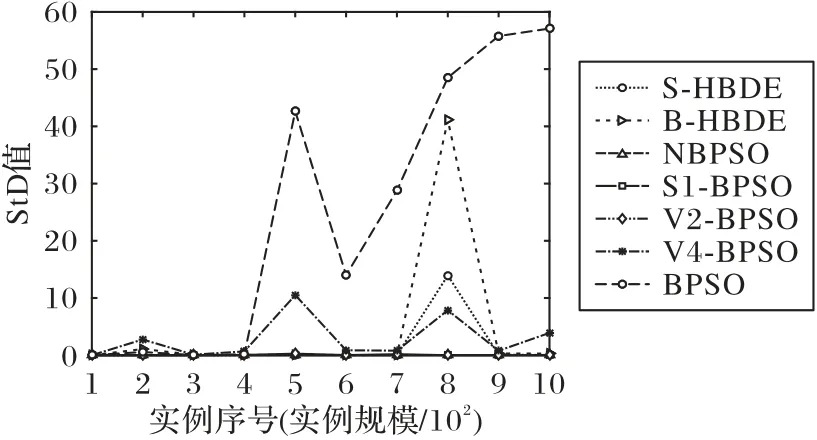
图9 求解实例skpc100~skpc1000的StD曲线Fig.9 StD curves in solving instance skpc100-skpc1000
综上所述,NBPSO 的计算结果与算法稳定性均比S-HBDE、B-HBDE、S1-BPSO、V2-BPSO、V4-BPSO和BPSO的更好,它是求大规模KPC实例的一个新的高效演化算法。
5 结语
本文首先介绍了常见的S型和V型转换函数,然后基于V型转换函数给出了一种新的S 型转换函数。在此基础上,提出了一种基于新的S 型转换函数的二进制PSO 算法NBPSO。为了验证NBPSO 的性能,对四类大规模KPC 实例进行了仿真计算,计算结果表明:NBPSO 与基于其他转换函数的二进制PSO、DS-BPSO、S-HBDE、B-HBDE 和BPSO 相比,在平均计算结果和鲁棒性方面有着明显地改善,因此是求解KPC 的一个高效新算法。在未来研究中,我们将探索新S 型转换函数对其他二进制算法的影响,如二进制差分算法[12]、二进制灰狼优化算法[17]等。此外,利用NBPSO 求解其他组合优化问题如集合覆盖问题[18]、设施选址问题[19]等也是一个值得今后探讨的问题。

