快速压排载系统空压机组启停控制策略设计
尹石军,林召凯,高海波,李孟春,武美君
(1.招商局重工(江苏)有限公司,江苏 南通 226116; 2.武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
0 引 言
半潜式起重拆解平台快速压排载系统的空压机组由4台空压机组成。在日常作业过程中,半潜式起重平台需要长时间不间断工作,而对于单台空压机而言,长时间不间歇工作可能会带来负荷过重、温度持续升高等问题,从而导致空压机使用寿命缩短,也会对空压机供气系统的安全性、稳定性产生一定的影响。因此,开发一套智能控制系统用于控制空压机的启停,在保证作业安全的同时实现几台空压机轮换工作,成为研究重点。
采用基于模糊控制理论的方法实现对快速压排载系统空压机组的智能启停寻优策略,通过不同的典型工况算例模拟验证所设计的寻优策略是否达到理想效果。
1 寻优策略总体设计
在半潜式拆解平台空压机组中,空压机的配置及控制可有两种方案:方案一,配置4台空压机,分为2组,同时启停且分别通过压缩空气管系连通主浮筒及辅浮筒;方案二,配置4台空压机,两用两备,采用阶梯式控制空压机的启停,通过环形压缩总管连通主浮筒和辅浮筒。以第二种方案为研究背景,为体现寻优启停策略的效应,对方案二进行以下修改:不对常用机进行特定设置,仅要求处于启动状态的空压机台数在同一时刻不超过2台。令运行着的空压机数量S∈[0,2];设定空压机编号M∈{1,2,3,4};设空压机的累计运行时长为TR,那么每台空压机累计运行时长为TR1、TR2、TR3、TR4。设空压机停止时间间隔时长为TST,那么每台空压机停止间隔时长为TST1、TST2、TST3、TST4。图1所示为寻优控制策略原理图。寻优控制策略主要由3部分组成,分别为空压机运行台数的确定、累计运行时长比较、模糊控制。
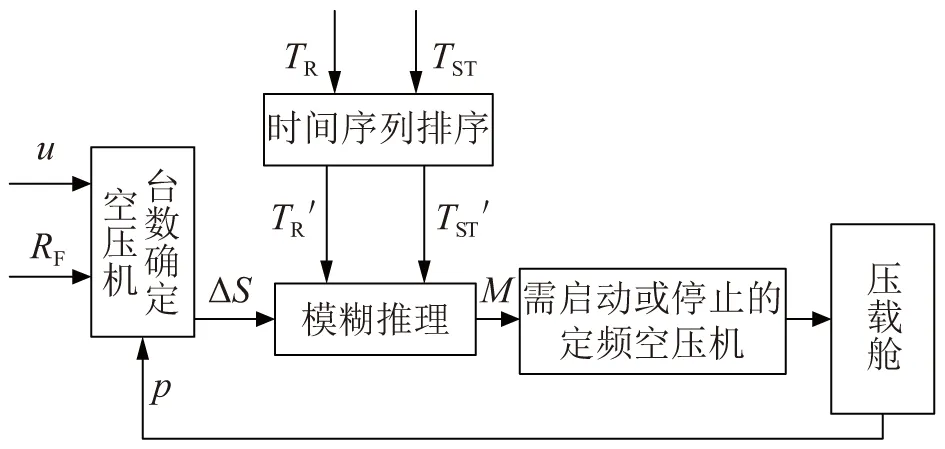
图1 寻优控制策略原理图
由于空压机组采用阶梯式控制方式,确定空压机台数的输入变量为RF、u、p。其中空压机运行返回信号RF(表示当前空压机加/卸载情况)与压载舱内的压力p有关,控制量u由压力偏差变化率de/dt调节。根据空压机运行返回信号RF、压载舱内的压力p和控制量u计算空压机运行台数变化量ΔS。然后将ΔS作为输入引入模糊推理模块中,再根据空压机运行累计时长TR、停止时长TST推导出空压机运行时长排序T′R、停止时长排序T′ST,再将排序结果作为输入引入模糊推理模块中,推理出应该启动或停止的空压机编号M。
2 空压机运行规则
2.1 启动数量
空压机加载压力分别为0.17 MPa、0.20 MPa,空压机卸载压力分别为0.20 MPa、0.26 MPa。当u>0时,舱内的空气压力是上升的,当空气压力低于0.17 MPa时,2台空压机同时加载,输出ΔS=2; 当u>0,快排舱内的空气压力大于0.20 MPa且低于0.26 MPa时,1台空压机卸载,输出ΔS=-1; 当u>0,快排舱内的空气压力大于0.26 MPa时,2台空压机卸载,输出ΔS=-2; 当u<0,空气压力大于0.17 MPa且低于0.20 MPa时,1台空压机加载,输出ΔS=1; 当u<0,空气压力低于0.17 MPa时,2台空压机加载,输出ΔS=2; 当u=0时,舱内压力达到设定值,空压机需全部卸载,此时输出ΔS=-2。
2.2 时长序列
由于每台空压机累计运行时长的排序都可能是第一或者最后,停止累计时长也一样,因此设定空压机组中的每台空压机累计运行时长序列为T′Ri∈{1,2,3,4},而每台空压机累计停止时长序列为T′STi∈{1,2,3,4}。
2.3 运行规则
当系统需要供气时,选择累计停止时长TSTi(i∈{1,2,3,4})中累计时间最长的2台空压机启动;在整个系统运行期间,为保证每台机器的工作时间平衡,需要对所有空压机进行轮换使用,轮换的时间间隔初步设定为12 h,当台数变化量ΔS=-1时,需要停止1台空压机的运行,选择空压机组累计运行时长TRi(i∈{1,2,3,4})中运行时长最长的1台空压机。这种设计能够避免某台机器因长时间不间断工作而疲劳运行,缩短使用寿命。考虑到对空压机进行轮换可能会影响管路压力的波动,因此应该在用气需求小的时候进行操作。在选择需要启动的空压机时寻优范围将不包括已经处于启动状态的空压机,在选择需要停止的空压机时寻优范围将不包括已经处于停止状态的空压机。
3 模糊逻辑控制器设计
模糊逻辑控制器设计流程如图2所示,按照此设计流程,结合所设计的空压机智能寻优策略,选取制定相对应的模糊控制器[4]。
监测对象为所有处于产茶阶段的茶园种植区和茶农散种区。茶园种植区定义为集中连片面积150亩以上的图斑,茶农散种区定义为集中连片面积1.5亩以上图斑,图斑勾绘边界几何精度为 1m。
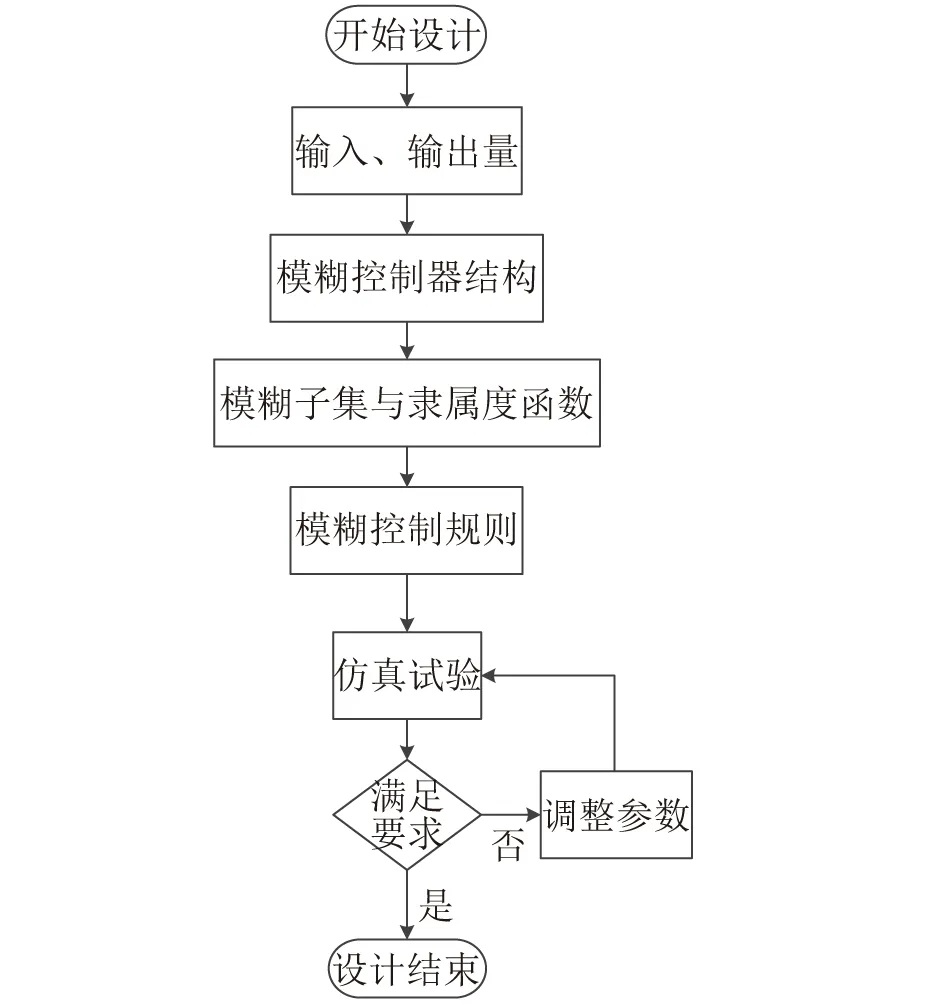
图2 模糊逻辑控制器设计流程
3.1 寻优启动模糊控制器设计
寻优启动控制是将空压机累计停止时长序列T′STi∈{1,2,3,4}、运行台数变化量ΔS∈{0,1,2}作为寻优启动的2个输入变量,将需要启动的空压机编号M1i∈{1,2,3,4}作为输出变量。
(1) 模糊化处理
2个输入变量和1个输出变量的基本论域为
(1)
在确定2个输入变量和1个输出变量的基本论域后,需要确定其模糊论域,设定其模糊论域为
(2)
基本论域与模糊论域之间的映射需要有系数将其连接起来,根据BESIKCI等[5]的方法,计算得出输入变量ΔS和TSTi的量化因子、M1的比例因子分别为
(3)
(2) 确定模糊子集与隶属度函数
对系统中的变量确定模糊子集,选择3个模糊子集对ΔS进行模糊表示,即ZO、PS、PB,选择4个模糊子集对T′STi进行表示,即SS、XX、MM、LL,选择5个模糊子集对M1i进行描述,即ZO、FI、SE、TH、FO分别为
(4)
通过上述设定,确定2个输入变量和1个输出变量的模糊子集的隶属度函数均选用三角函数。
(3) 模糊控制规则和模糊推理
模糊控制规则制定得越详细,控制后的输出结果越精确。参考陈勇[6]的研究,根据快速排载系统的真实情况使寻优启动控制器按照表1规则进行变化,并选取Mamdani算法作为模糊推理法,达到较好的控制效果。
3.2 寻优停止模糊控制器设计
寻优停止控制是将空压机累计运行时长序列、运行台数变化量作为寻优停止的2个输入变量,将即将停止运行的空压机编号作为寻优停止控制的输出变量。
寻优停止模糊控制器的设计过程与寻优启动基本一致,选用二维Mamdani模糊控制器,各个空压机控制器的模糊子集在论域上的隶属度函数选用三角函数。表2为寻优停止输入输出变量参数。表3为寻优停止模糊控制规则表。
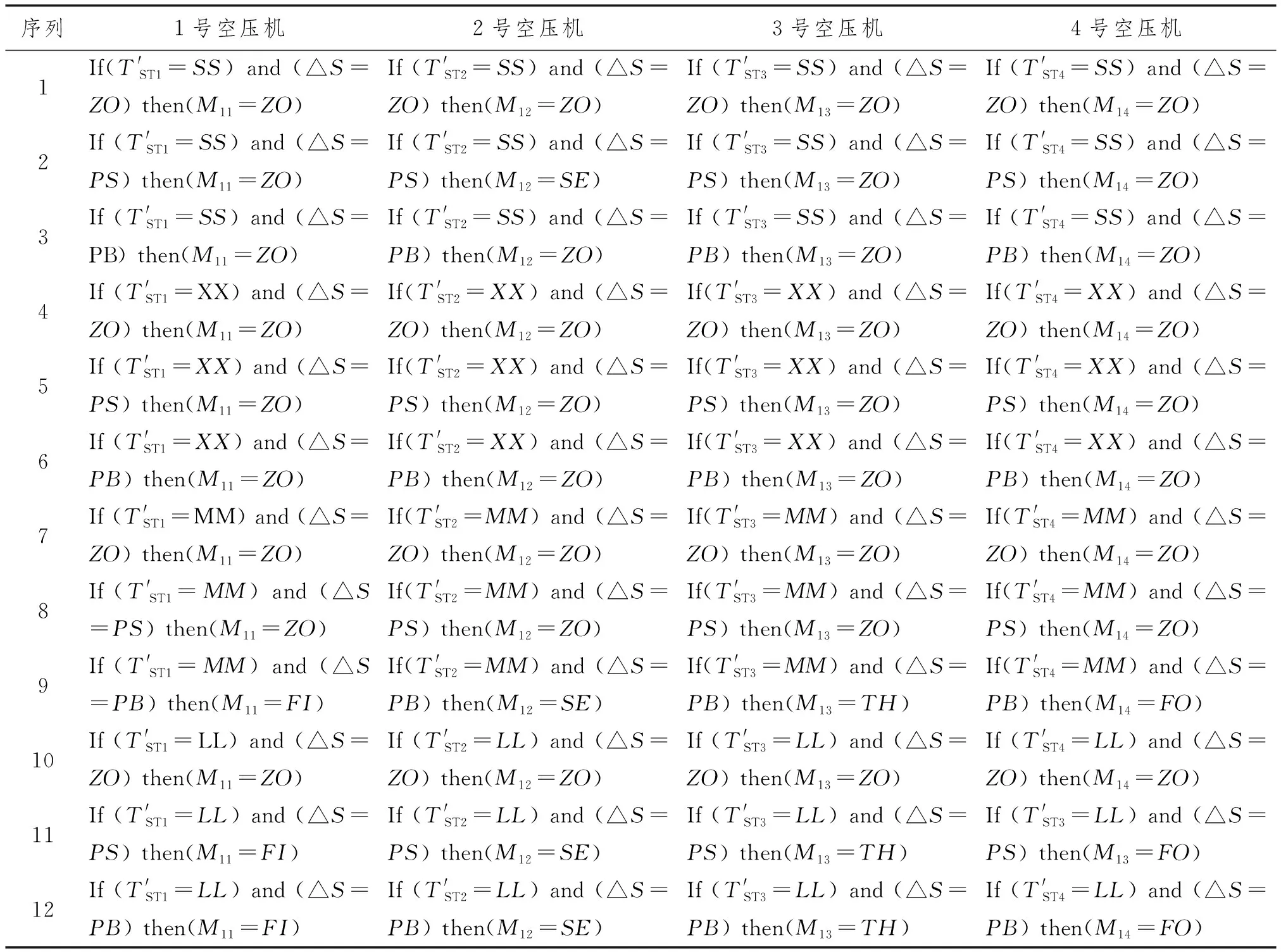
表1 寻优启动模糊控制规则

表2 寻优停止输入输出变量参数

表3 寻优停止模糊控制规则
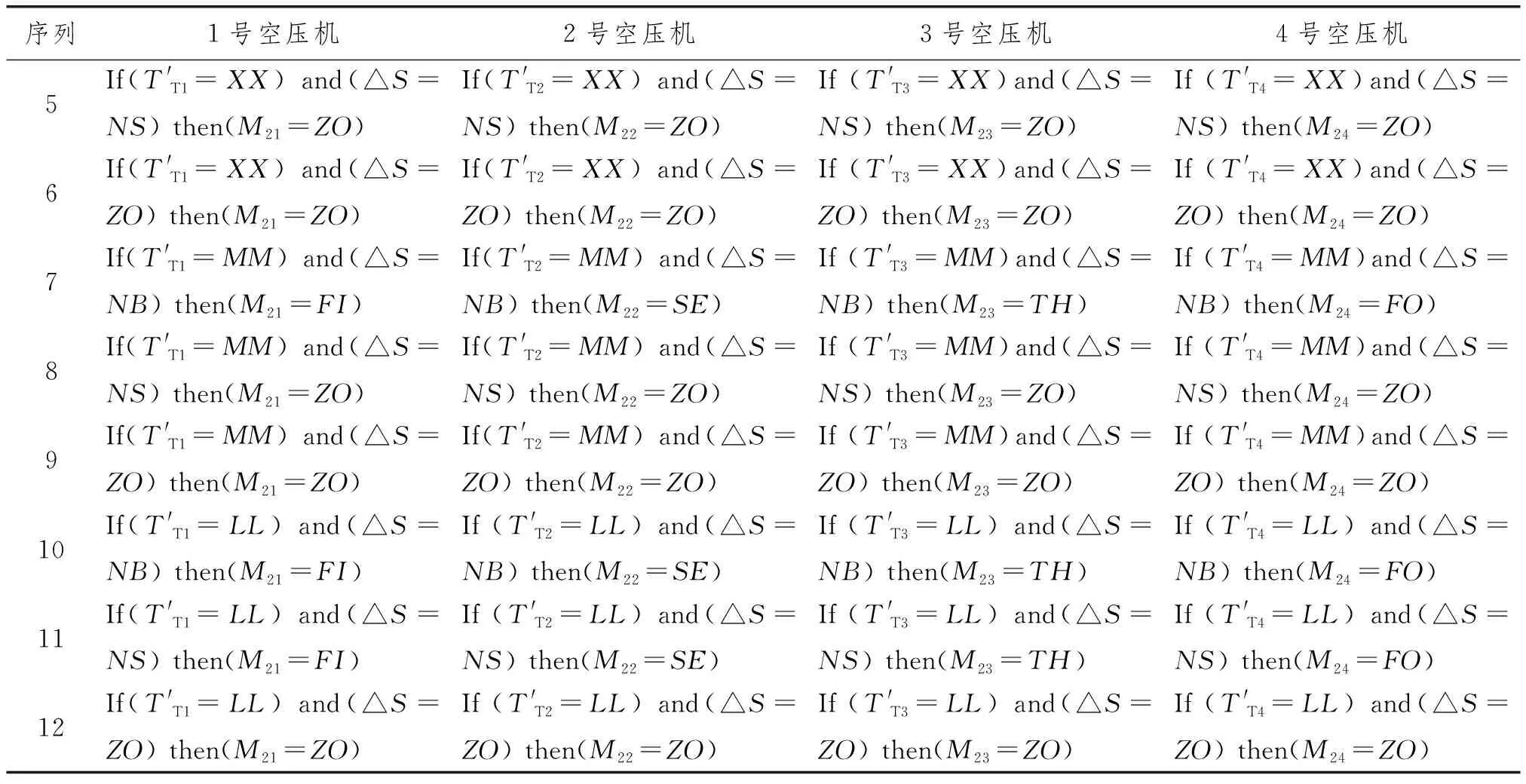
续表3 寻优停止模糊控制规则
3.3 寻优策略实现
根据模糊规则可以得到空压机编号M对应的模糊关系矩阵R为
(5)
式中:RM1、RM2分别为寻优启动和寻优停止的模糊关系矩阵;Uij(ΔS×T′STi)、Uij(ΔS×T′Ri)分别为模糊析取ΔS与T′SRi,ΔS与T′Ri的模糊关系输入矩阵;UM1ij、UM2ij分别为模糊关系的输出矩阵。在得到模糊关系矩阵后,模糊子集U为
(6)
式中:UM1、UM2分别为寻优启动和寻优停止的模糊子集; ΔS(n)为激活第n条规则的ΔS输入;TSTi(n)、TRi(n)分别为激活第n条规则的TSTi与TRi输入。 模糊推理出来的值为模糊值采用加权平均法进行清晰化的计算结果。在经过清晰化处理后得到数值仍然属于模糊论域,需要再乘以比例因子才能变换到基本论域[7]。根据表1和表2,得到模糊子集UM1(n)、UM2(n),对于离散化的隶属度函数可按照式(7)加权平均法进行计算:
(7)
式中:μM1(n)、μM2(n)分别为第n条规则在寻优启动和寻优停止输出的输出结果所占的权重。再对输出的中位数UMi(U)清晰化得到输出量M,即需要停止或者启动的空压机编号。
(8)
式中:KM1=KM2=0.67为比例因子。
4 寻优策略验证
综合上述模糊规则,再对这些规则进行整合,整合后的最终结果便是完整的寻优控制策略。整个寻优策略的输入变量为u、RF、TR、TST和p,将上述变量作为基础,设计3种模拟算例进行测试验证,并以算例一做详细说明。
(1) 当TST={6.7,3,10,5}、u=-0.1、RF=Ø、TR={9,12,6,10}、P=0.19 MPa时,由运行规则可知ΔS=1,即为了满足供气需求,此时应当运行一台空压机。考虑到平衡空压机运行时间的目的,应当启动当前累计停机时间较长的一台,由TST1=MM、TST2=SS、TST3=LL、TST4=XX可知,3号空压机累计停机时长最长。因此输出启动空压机编号M1={3},即启动3号空压机。
(2) 当TST={1,0.3,3,2}、u=-0.1、RF=Ø、TR={3,5,2,2.5}、P=0.16 MPa时,由空压机运行规则可知ΔS=2,此时没有空压机正在运行,由TST1=XX、TST2=SS、TST3=LL、TST4=MM可知,3号与4号空压机累计停止时长相对1号与2号较长,因此模糊推理得到启动空压机编号M1={3,4}。
(3) 当TST={0.3,2,1.1,1}、u=0.32、RF={1,4}、TR={7,5,5.8,6}、P=0.21 MPa时,由空压机运行规则可知ΔS=-1,此时1号和4号空压机正在运行,而根据TR1=LL、TR4=MM,1号空压机比4号空压机累计运行时长更长,因此输出停止空压机编号M2={1}。
由上述测试数据可知,改变输入变量u、RF、TR、TST、P的值,再依据模糊规则得到控制信号,可以改变各个空压机的运行状态,且避免了单台空压机不间断运行的问题,延长了整体空压机组的寿命。
5 结 语
以快速排载系统的空压机组为研究对象,提出一种基于模糊理论的空压机启停控制寻优策略,为空压机的启停建立详细的模糊规则,经模拟算例验证,该寻优策略能够达到平衡空压机组运行时间的效果。

