波流激励作用下导管架式升压站疲劳损伤
袁建平,陈杰峰,孙震洲
(1. 浙江省深远海风电技术研究重点实验室,浙江 杭州 311122;2. 中国电力建设集团 华东勘测设计研究院有限公司,浙江 杭州 311122)
0 引 言
近年来我国对海洋石油、海上风能的开发愈加重视,海洋结构作为这类能源开发的主要支撑载体,其安全服役意义重大。海上升压站结构长期处于波浪载荷和海流载荷等交变载荷作用下,平台结构节点处将产生随时间变化的复杂应力,该交变应力将导致平台结构的疲劳损伤,平台结构的疲劳损伤累积到一定程度可能进一步引起整个平台结构的失效。因此,为保证平台结构在波浪载荷作用下能够达到设计寿命,避免失效引起人员伤亡和经济损失,其疲劳寿命预测至关重要。
针对海洋结构的疲劳损伤,近年来相关学者基于不同分析方法开展了大量研究。莫继华[1]借助Abaqus计算程序研究金海风电机组单桩支撑结构的疲劳损伤,并预测其疲劳寿命。梁园华等[2]基于谱疲劳分析方法分别采用确定性疲劳分析方法和疲劳可靠性分析方法分析张力腿平台(Tension-Leg Platform,TLP)平台NODE结构的疲劳损伤,结果显示,与疲劳可靠性分析方法相比,确定性疲劳分析方法更为保守。YAN等[3]结合裂纹扩展的单一曲线模型、基于有限元子模型技术的应力强度因子求法以及基于谱分析的疲劳载荷谱产生方法,对某半潜式钻井平台典型焊接节点进行基于裂纹扩展疲劳寿命预报,结果表明,该半潜式平台焊接结构符合设计寿命的要求,初始裂纹尺寸对疲劳寿命影响较大。李珊珊等[4]介绍载荷次序效应问题的研究现状,归纳了考虑载荷次序效应的变幅载荷作用下结构疲劳裂纹扩展模型,并说明所应用的疲劳寿命预报统一方法(Unified Fatigue Life Prediction,UFLP)的基本思想,给出随机载荷作用下,应用UFLP计算海洋结构物疲劳裂纹扩展的示例。VELDKAMP[5]给出风机疲劳分析过程中影响疲劳载荷的随机参数目录,可确定材料的疲劳失效概率。王彦红[6]分析随机波浪载荷作用下风机支撑结构的波浪谱频域疲劳损伤情况。刘建军[7]研究整体桁架式支撑结构的动力特性和疲劳损伤,采用线性叠加方法分析各疲劳载荷作用下结构损伤情况。付春等[8]提出基于子结构法的海洋平台疲劳可靠性评价方法,并选择一个平面桁架和导管架型海洋平台进行疲劳可靠度计算方法验证,结果表明所提方法可以简化大型结构的复杂程度,减小疲劳计算的工作量。李明等[9]基于ANSYS有限元软件计算管节点的热点应力,并基于S-N曲线分析平台构件的疲劳损伤。修宗祥等[10]以某200 m水深导管架平台结构为例,基于有限元方法计算各疲劳子工况下平台的动力响应,基于Miner线性疲劳累积损伤准则和结构可靠性理论分析平台的疲劳寿命。韩超帅[11]研究海上风机支撑结构的风载荷及波浪载荷,在此基础上计算不同加强形式管节点的应力集中系数,并基于SACS软件计算风载荷和波浪载荷作用下管节点的疲劳损伤。张凤[12]基于ANSYS Workbench软件分析渤海某平台结构在风浪载荷作用下管节点热点焊缝的应力时程,并对其疲劳寿命进行预测。冯加果等[13]基于ANSYS软件提出海洋平台局部构造疲劳寿命评估方法,采用简化的疲劳计算方法分析某海洋结构裙桩套筒结构的疲劳损伤。石锐峰[14]计算波浪载荷作用下TLP浮式风机结构的动力响应,并基于线性累积损伤理论,运用时域方法分析优化前后结构的疲劳寿命。
本文针对某海上风电升压站平台,根据其工作海域全年范围波浪散布图,计算不同波浪工况下的动力响应,并采用有限元方法分析该平台不同管节点的热点应力。在此基础上,基于Miner线性累积损伤准则和雨流计数方法,依据规范选择相应S-N曲线,计算管节点在全年波流作用下该平台的疲劳损伤情况,预测平台结构的疲劳寿命。
1 疲劳分析理论
1.1 波流载荷计算理论
(1) 波浪载荷
导管架式升压站是一种典型的由多种规格杆件构成的空间桁架结构,其杆件直径与波长之比远小于0.2,可按照小尺度结构件承受的波浪载荷进行计算。常见的波浪理论包括孤立波理论、微幅波理论和Stokes波理论等。结合该平台所处海域,波浪载荷采用Stokes五阶波理论进行计算。
针对小尺度管截面构件,其单位长度所受波浪力可采用Morison方程[15]进行计算:
(1)
式中:f为构件单位长度所受波浪力,N;CD为垂直于构件轴线的阻力系数,管截面构件通常取0.6~1.0;ρ为海水密度,取1 030 kg/m3;D为平台构件直径,m;u为水质点垂直于构件轴线的速度分量,m/s;CM为惯性力系数,取2.0。
(2) 海流载荷
当仅考虑海流作用时,管截面构件单位长度的海流载荷为
(2)
式中:fD为海流作用力,N;A为单位长度构件垂直于海流方向的投影面积,m2/m;UC为设计海流速度,m/s。
1.2 海上升压站动力响应分析
根据结构动力学理论,当升压站结构受到波浪、海流等外载荷作用时,其动力方程[16]为
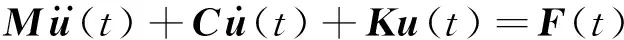
(3)

C=αM+βK
(4)
式中:α为质量阻尼系数;β为刚度阻尼系数。质量阻尼系数和刚度阻尼系数与结构系统前两阶固有频率有关:
(5)
式中:f1和f2为结构系统前两阶固有频率;ξ为结构黏性阻尼比,取0.03~0.05。
1.3 Miner线性累积损伤准则
海洋结构疲劳损伤分析通常采用Miner线性累积损伤理论。该理论假设当海洋环境载荷作用于结构时结构产生一定应力,在该应力水平条件下,结构累积损伤的速度与载荷的先后无关。当长期应力范围分布由一个应力时间历程表示时,依据Palmgren-Miner理论,疲劳损伤度D1[17]为
(6)
式中:ni为特定应力范围的应力循环次数;Ni为基于S-N曲线应力范围失效的载荷循环平均次数;k为考虑应力变化范围的间隔次数。通常认为D1=1时结构构件发生破坏。
1.4 雨流计数法
雨流计数法[18]是一种统计载荷幅值循环次数的方法,也称为塔顶法。其根据计算得到的载荷时程,统计出其所有的载荷循环次数和全循环幅值,根据载荷幅值可以绘制出其频次直方图。
雨流计数法假设载荷时程图中时间轴垂直向下,想象雨滴沿载荷时程曲线内侧流下,如图1所示,依据雨滴运动轨迹得到载荷循环次数,并推算各循环载荷幅值。其技术准则通常有以下4条:
(1) 重排载荷历程,以载荷时程图中峰值或谷值为雨滴起点。
(2) 雨滴由每个峰(谷)值内侧向下运动,于下一个峰(谷)值点落下,直至下方有大于(小于)起始时刻峰(谷)值为止。
(3) 当雨滴遭遇上方流下的雨滴时停止运动。
(4) 记录所有循环及各循环幅值和均值。

图1 雨流计数法示例
1.5 S -N曲线
S-N曲线通常根据构件疲劳试验数据绘制,一般为试验数据的平均值与二倍标准差的差值,其具有97.6%的存活率。根据管节点的几何形状以及其他诸如载荷方向、可能的装配/检测方法等因素可以将节点分为不同类别并具有不同的设计S-N曲线。设计中的S-N曲线在双对数坐标下一般由一段或者两段直线组成,如图2所示。

图2 双线段S -N曲线示例
对于实际工程中的疲劳分析,通常将焊接接头分为不同的级别,每一级别都对应相应的S-N曲线。S-N曲线表达式[17]为
lgN=lgK1-m1lgS
(7)
当失效的循环次数大于Nq时,失效时应力循环次数N与应力范围的关系为
lgN=lgK2-m2lgS
(8)
式(7)和式(8)中:N为应力范围S作用下预计产生的循环数量;S为应力范围; lgKi(i=1,2)为S-N曲线在lgN轴的截距;mi(i=1,2)为S-N曲线的负斜率。
2 海上升压站导管架平台模型
该平台为4桩腿钢质导管架结构,平台结构如图3和图4所示。图中海平面高程为±0 m,平台共5层,层间由斜撑交叉连接,每层设有水平十字交叉支撑。结构材料为结构钢,密度为7 850 kg/m3,泊松比为0.3。平台上部模块总质量约3 000 t。

图3 平台立面结构图
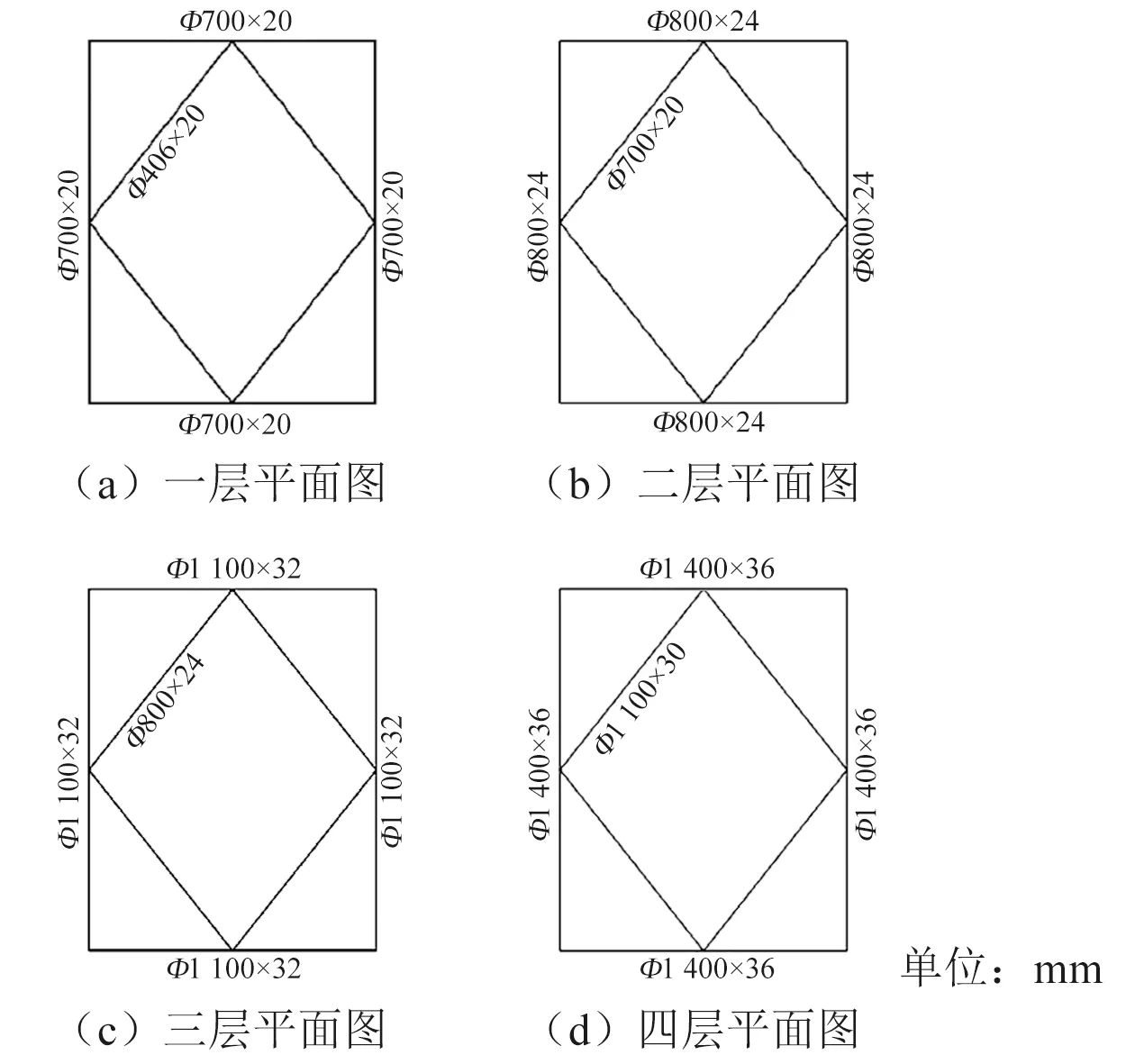
图4 平台各层结构图
根据平台结构尺寸,建立该平台有限元模型,如图5所示。水下杆件采用Pipe 59单元,在该单元计算过程中可考虑波浪及海流载荷;水上杆件为Pipe 16单元。上部模块质量以集中质量的方式加载至平台顶层中心位置。
根据结构节点结构型式,分别选取平台各层3个不同结构型式节点,计算其疲劳损伤情况,计算节点分别为29、67、89、124、153、197、235、269、452、564、660。

图5 平台有限元模型
3 波流载荷作用下平台动力响应
该平台所在海域全年波浪散布图如图6所示。

图6 平台所在海域全年波浪散布图
基于该波浪散布图,逐一计算各海况作用下平台疲劳损伤及寿命,按照各海况在波浪散布图的概率分布,对所得疲劳损伤和寿命进行加权统计,即可获得该平台疲劳寿命。
以波浪散布图中周期7.38 s、波高2.66 m海况为例,该海域表面流速约1.45 m/s、中部流速约1.30 m/s,底部流速约1.21 m/s。将上述载荷条件加载至平台,计算该海况下平台所选节点应力时程,如图7~图17所示。

图7 节点29应力时程

图8 节点67应力时程

图9 节点89应力时程
图10 节点124应力时程

图11 节点153应力时程

图12 节点197应力时程

图13 节点235应力时程
图14 节点269应力时程
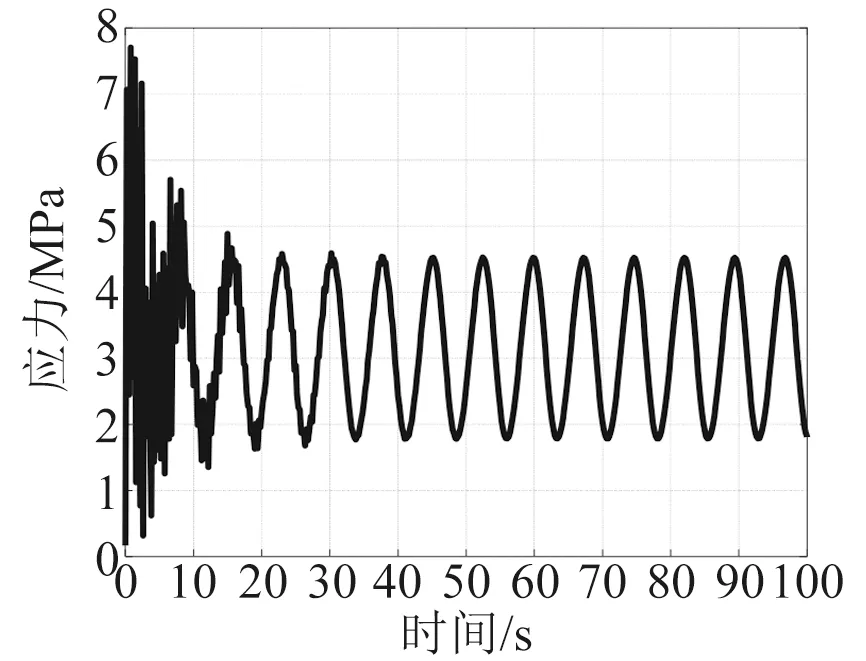
图15 节点452应力时程
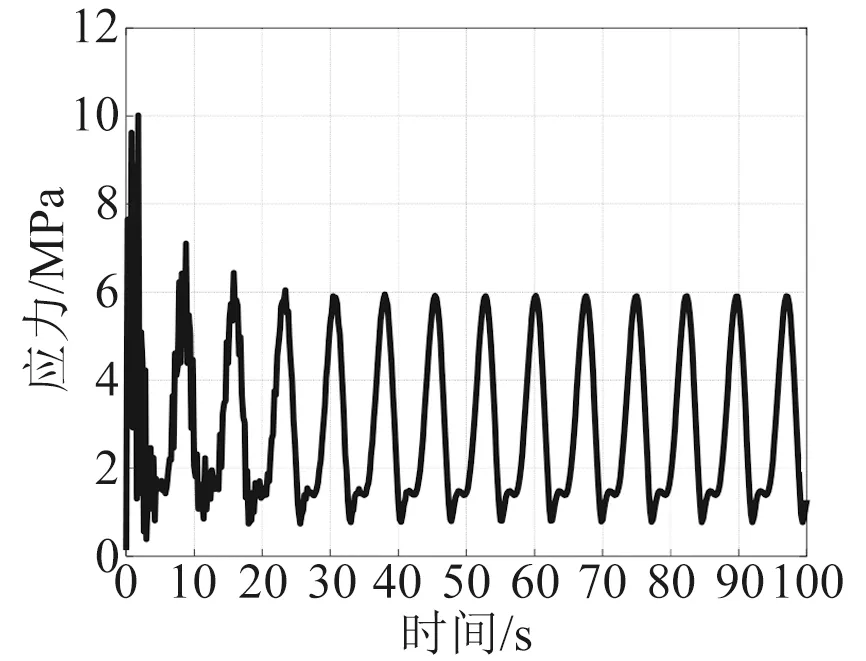
图16 节点564应力时程
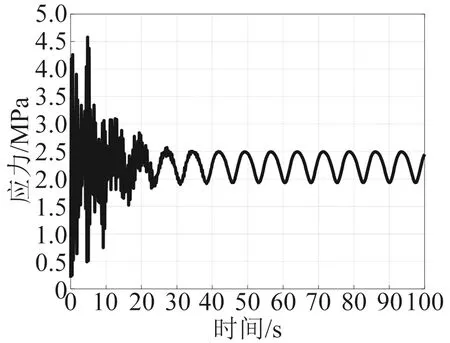
图17 节点660应力时程
3 管节点热点应力
导管架平台主支撑管与弦管相交位置应力状态通常较为复杂,存在应力集中现象。管节点局部应力最大的点称为热点,其应力称为热点应力,热点应力对于结构疲劳影响至关重要,因此有必要确定各海况作用下各节点的热点应力分布。
采用有限元方法对所选节点分别建立精细有限元模型,将管节点附近相邻杆件从整体结构中分离出来,在远离热点区域位置将主支撑管或支管从节点处断开,并提取该截断位置节点位移和转角,将其作为边界条件加至局部管节点模型,计算其应力分布情况,并采用外推法计算各节点热点应力幅值。得到各节点热点应力结果如图18~图28所示。

图18 节点29热点应力分布
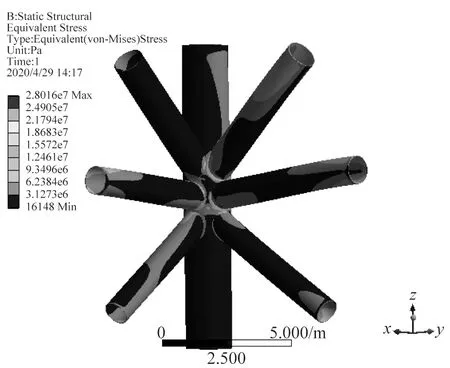
图19 节点67热点应力分布
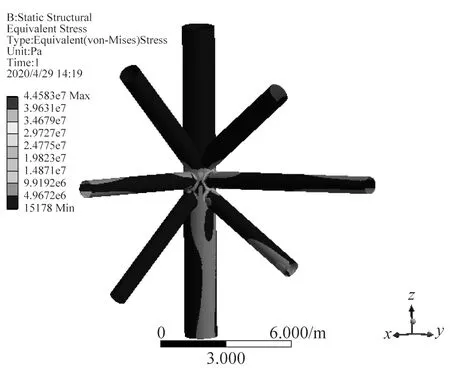
图20 节点89热点应力分布

图21 节点124热点应力分布
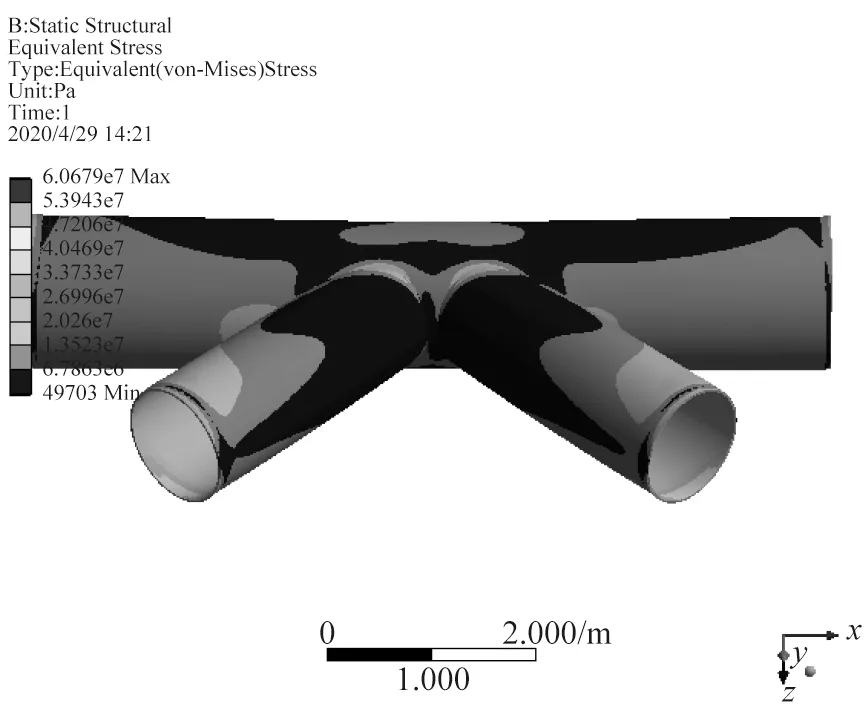
图22 节点153热点应力分布
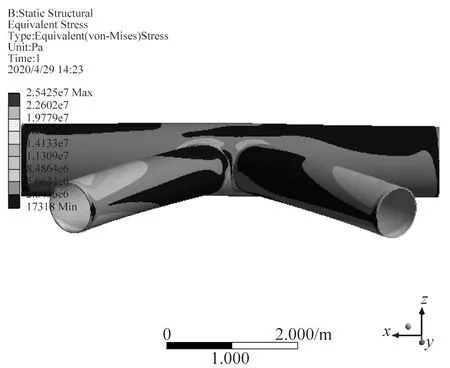
图23 节点197热点应力分布

图24 节点235热点应力分布
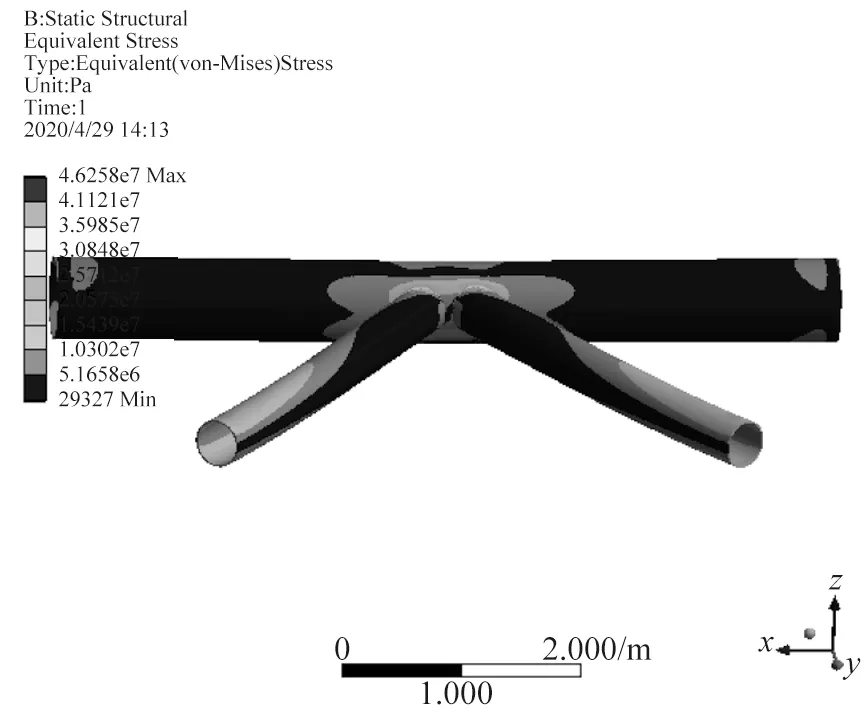
图25 节点269热点应力分布
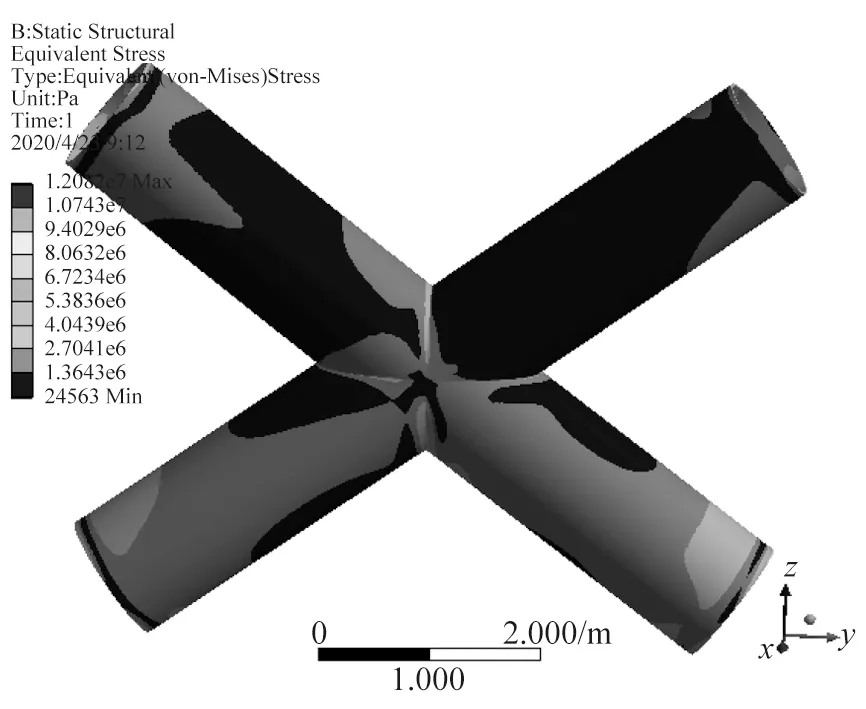
图26 节点452热点应力分布

图27 节点564热点应力分布
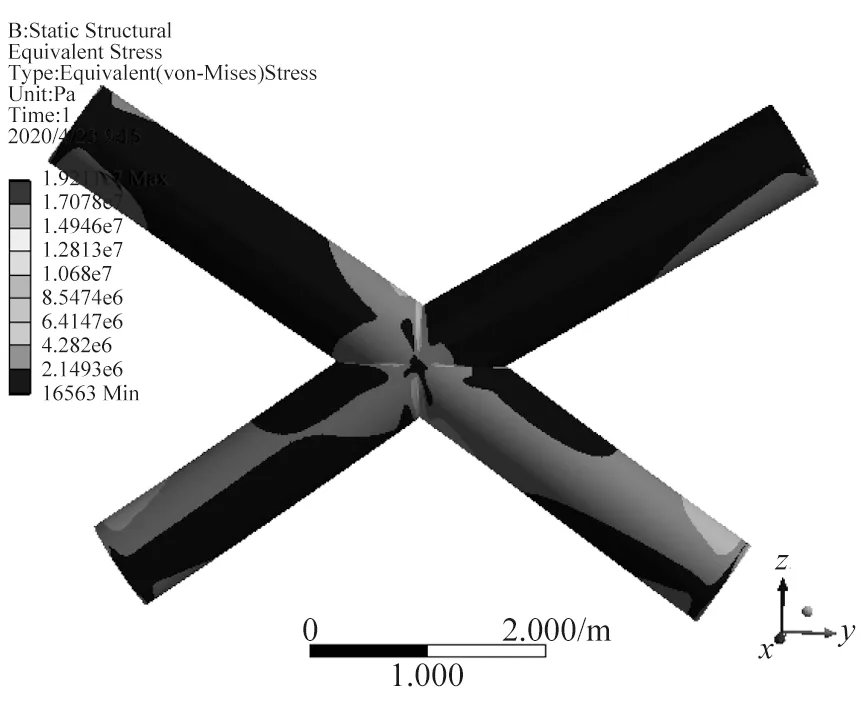
图28 节点660热点应力分布
4 平台疲劳寿命计算
该平台管节点疲劳损伤计算S-N曲线选用中国船级社《海洋工程结构物疲劳强度评估指南》推荐的WJ(焊接类节点)型S-N曲线,如图29所示,其在空气中和海水腐蚀作用下K和m取值如表1所示。
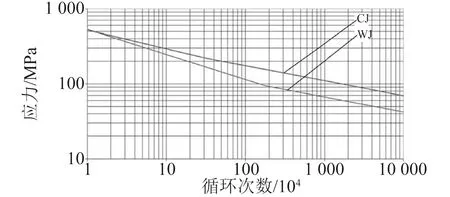
图29 管节点在海水中有效阴极保护环境下的设计S -N曲线
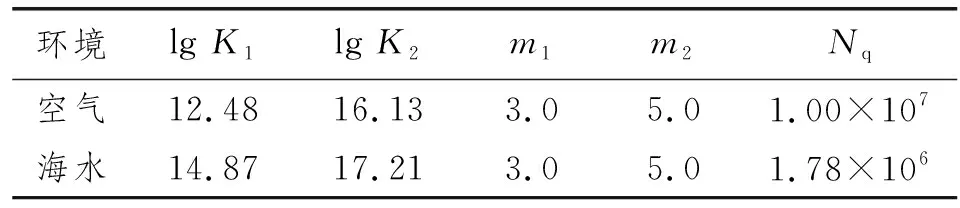
表1 管节点S -N曲线参数取值
按照线性累计损失准则,根据热点应力幅值及应力时程数据,按照S-N曲线数据,计算各节点的年疲劳损伤度和疲劳寿命,结果如表2所示。

表2 在周期7.38 s、波高2.66 m海况作用下所选节点疲劳损伤情况
由表2可知,该海况作用下平台节点67的年疲劳损伤最大,约0.026 6,寿命约37.60 a。
按照上述方法分别计算波浪散布图中各海况作用下节点的疲劳损伤情况和疲劳寿命。依据各海况在波浪散布图的概率分布,对各海况下平台的疲劳寿命进行加权求和,得到该平台在全海况范围内疲劳寿命约33.43 a,满足设计寿命不小于25 a的要求。
5 结 论
针对某海上风电升压站导管架平台,建立有限元模型,分别计算波浪散布图内各海况作用下不同结构型式节点的应力时程分布情况。建立不同结构型式节点的精细有限元模型,提取截断处节点的位移和转角信息施加至有限元模型,采用外推法获取不同结构型式节点的热点应力幅值。根据Miner线性累积损伤准则,基于各节点的应力时程和热点应力幅值,计算波浪散布图中各海况作用下各节点的疲劳损伤情况及疲劳寿命,并基于波浪散布图中各海况的概率分布,对各海况作用下的平台疲劳寿命进行加权统计,结果显示该平台疲劳寿命约33.43 a,满足设计要求。

