破浪板对FPSO大型LPG储罐晃动的抑制作用

陈 静，潘大新，程久欢

(海洋石油工程股份有限公司，天津 300452)

0 引 言

浮式生产储卸油装置(Floating Production Storage and Offloading，FPSO)是长期飘浮在固定海域、不解脱的生产储卸油装置，当FPSO设有轻烃回收装置比如液化石油气(Liquefied Petroleum Gas，LPG)系统时，为满足穿梭油船的集输要求和时间间隔，同时避免对冷却介质的需求，通常需设置大型常温高压卧式LPG储罐[1]。很多FPSO地处台风高发海域，且LPG储罐一般直接布置在船体主甲板以上的模块平台上，位置高、晃动幅度大，罐内液体的晃动冲击甚至会破坏罐壁和罐体支持结构。

为减小并缓和FPSO晃动时储罐内的液体介质对储罐的冲击影响，通常可以在储罐筒体内设置横向破波结构，以减缓储罐内液体的波动，减小由液体介质波动产生的储罐壳体附加弯曲应力和冲蚀。该结构对储罐本身也有一定的加强，从而延长储罐寿命。由于流体运动的复杂性，经验公式的计算准确率较低，破浪板的设计与分析往往采用台架和水池试验方法，不仅需要设计和制作不同的实体模型，试验操作工况多且复杂，而且耗时长，造价也相对较高[2]。随着高性能模拟技术的发展，采用流体力学模拟计算的方式越来越多，可大幅节省试验成本并缩短工程周期[3]。

1 理论基础

晃动问题和建模基于自由表面的移动边界，求解移动边界的位置是建模的目标。目前捕捉自由表面的方法主要分为波面捕捉法和波面追踪法：波面捕捉法包括连续输运法、流体体积(Volume of Fluid，VOF)法、相位场法等，波面追踪法包括移动网格法、MAC(Marker and Cell)法等。从现有的方法看，VOF法更适用于自有界面的追踪，因为其在拓扑稳定性、局部守恒性和密实的界面间断宽度保持方面都更有优势。VOF法的基础是模拟流体晃动和气液交界面，其控制方程是三维不可压缩多相流非定常N-S方程[4]：

(1)

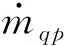
基本相的体积分数由所有相的体积分数之和为1的约束条件计算，而不用求解体积方程：

(2)

对于罐内的流体流动，采用湍流模型的k-ε双方程模型，该方程包含湍动能k和耗散率ε两个变量。

湍动能k的控制方程为

(3)

式中：ρ为密度；t为时间；ui、uj为速度；μ为动力黏度；μt为动力黏度系数；σk为常数。

耗散率ε的控制方程为

(4)

式中：v为运动黏度；vt为运动黏度系数；τ为应力张量；σs、Cs1、Cs2为常数。

具体求解可参照文献[5]，这里不再赘述。

在实际建模和计算中，假设流体的表面张力、温度变化和物性保持不变，忽略其变化。

2 晃动方程和边界条件

根据该FPSO船体晃动计算数据：在纵摇工况下，罐体晃动半径为75.7 m；在横摇工况下，罐体晃动半径为20.8 m。根据线速度、动压和速度管线，纵摇的线速度是横摇的3.5倍左右，动压是横摇的12倍左右，因此采用纵摇方向的晃动作为建模条件，且取最大晃动幅度值。晃动方程为

(5)

式中：θ为晃动角度；S为晃动幅度，最大值取7.95°；G为晃动周期，取10.023 s。

根据对大型液化天然气船液舱模型进行晃荡研究的资料[6-7]，当液舱在纵摇方向晃动时，液面位于70%罐体直径处是最危险的工况，因此模拟液位高度取70%罐体直径，即4.48 m。

其他边界条件包括：LPG储罐设计压力为1 760 kPa(表压)，重力垂直向下，初始状态时罐内液体处于静止状态，模拟过程时间取40 s。

3 试验验证

为验证建模方法及相关参数与实际情况的差别，采用Mikelis棱形液舱试验[8-9]进行数值模拟，并与试验结果进行对比。图1为具体的模型尺寸和压力测试点布置图。图2为监测点R2处压力分布与试验数据对比。图3为监测点R3处压力分布与试验数据对比。

图1 Mikelis棱形液舱模型

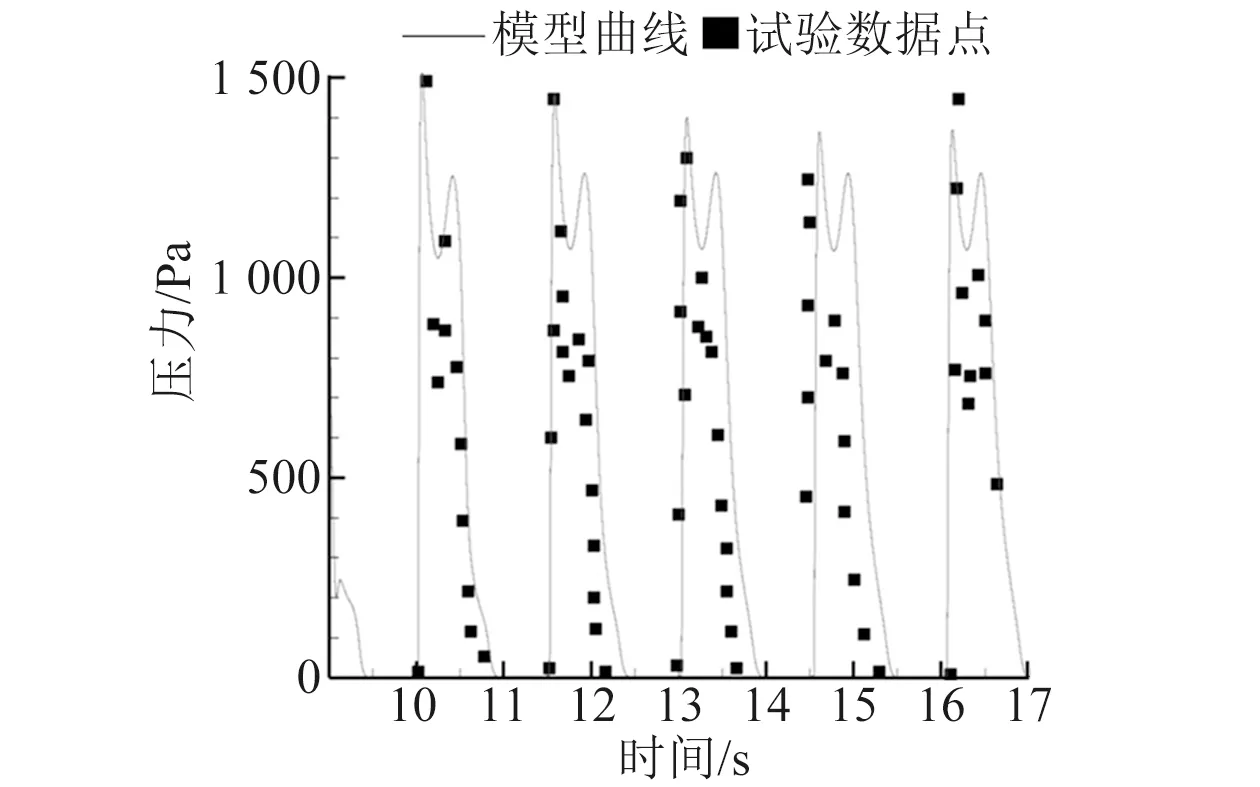
图2 监测点R2处压力曲线与试验值对比图

图3 监测点R3处压力曲线与试验值对比

由图2和图3可知，数值计算结果与试验结果吻合较好，可以采用该建模方法进行晃动模拟。

4 破浪板的设计

破浪板的设计通常包括安装数量、安装位置和破浪板面积。一般来说，破浪板上部弓形面积不应大于20%储罐横剖面面积，有效面积应大于40%横剖面面积。该FPSO的LPG储罐罐体尺寸为6.4 m(ID)×17.5 m(T/T)，设置2道厚度为6 mm的316SS破浪板，破浪板高度等于高液位报警点(5.4 m)，上部弓形面积约为储罐横剖面面积的10%。板上均匀布置直径为60 mm的小孔，开孔率约24.1%，有效面积为储罐横剖面面积的68.5%，满足一般设计要求。破浪板结构如图4所示。

图4 破浪板结构

5 计算网格

模型采用六面体网格与四面体网格混合划分，并在破浪板开孔处进行加密，网格总数为1 964 855个。图5为网格整体分布。图6为破浪板网格分布。

图5 网格整体分布

图6 破浪板网格分布

6 计算结果及分析

无/有破浪板的LPG储罐内液体分布模拟结果分别如图7和图8所示。从模拟结果可以看出，没有设置破浪板的LPG储罐的液面分布严重不平均，在某个时刻局部区域充满液体，局部区域充满气体，且液面晃动剧烈，无法保持气液界面，导致液体内部掺混气体形成气泡。在设置2个破浪板的LPG储罐中，液面被大致分为3个相对独立的区域，液体晃动程度小，且气液界面保持平稳。

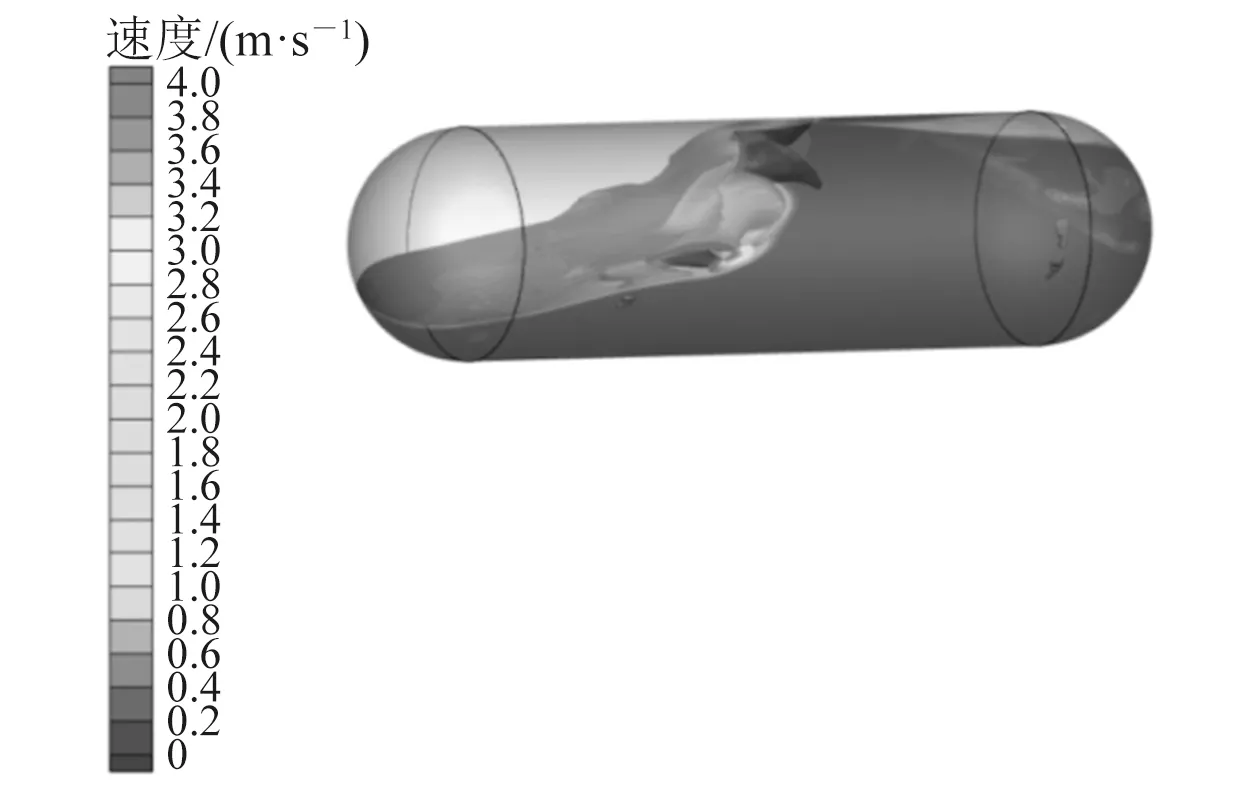
图7 无破浪板LPG储罐内液体分布

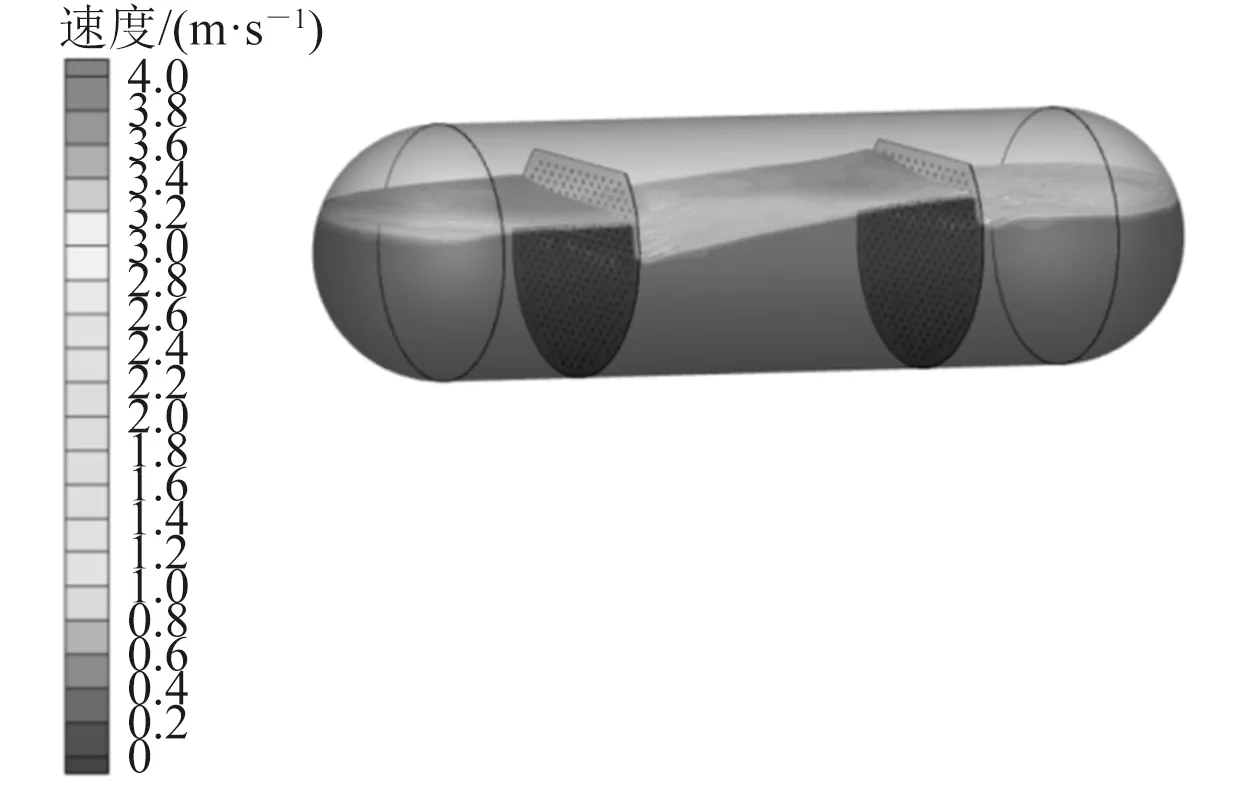
图8 有破浪板LPG储罐内液体分布

无/有破浪板的LPG储罐内压力分布模拟结果分别如图9和图10所示，模拟结果反映了罐体内液体和气体的压力分布。从模拟结果可以看出，在没有设置破浪板的LPG储罐中，由于液体晃动剧烈，相应的压力分布非常不均匀，尤其在封头部位出现局部压力较高的现象。在设置2个破浪板的LPG储罐中，由于液体分布稳定、均匀，因此压力分布较均匀，压力并不随着晃动的变化有较大波动。

无/有破浪板的LPG储罐封头在x轴向的受力随时间的变化模拟结果分别如图11和图12所示。由模拟结果可知，各部分的受力周期与LPG储罐晃动周期一致。对于无破浪板的LPG储罐来说，其封头在x轴向的最大受力达6×105N。对于设置2个破浪板的LPG储罐来说，其封头在x轴向的最大受力只有2×105N。

图9 无破浪板LPG储罐内压力分布

图10 有破浪板LPG储罐内压力分布

图11 无破浪板罐体受力(x方向)与时间关系

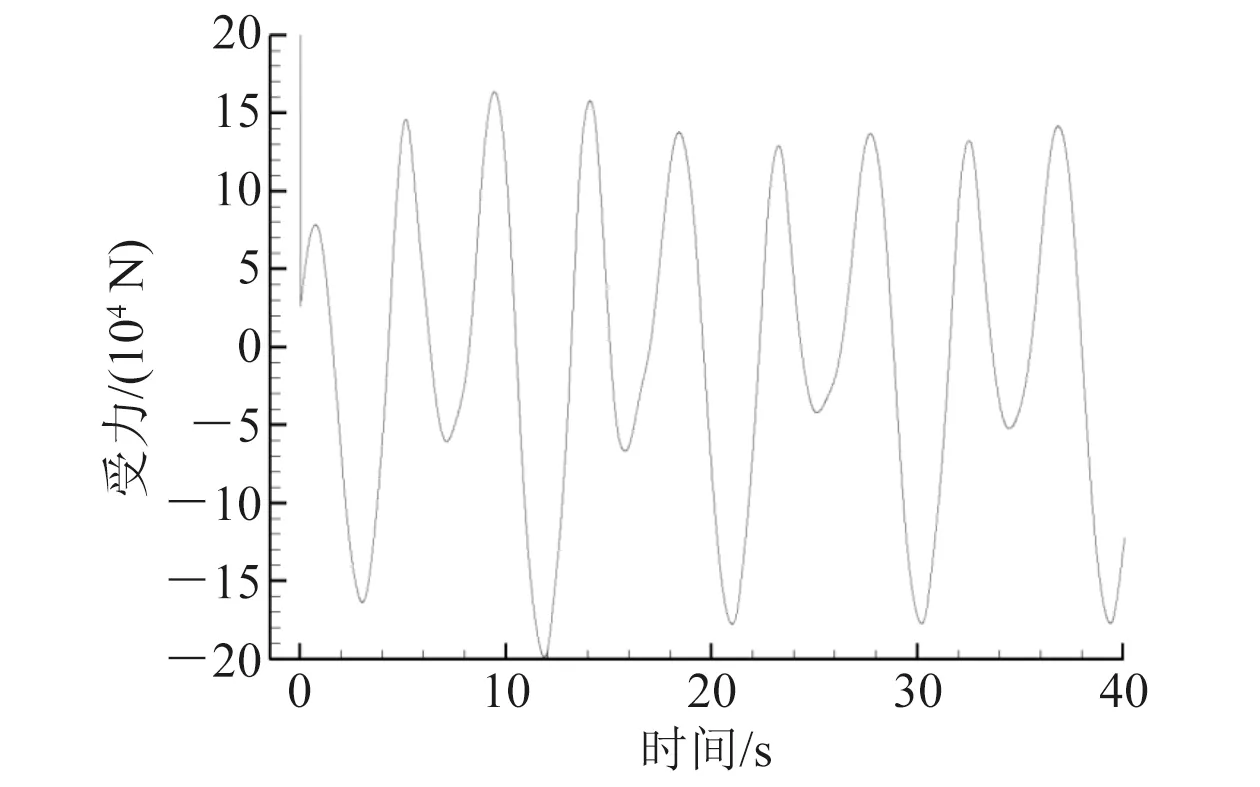
图12 有破浪板罐体受力(x方向)与时间关系

无/有破浪板的LPG储罐整体(即对封头1、封头2和壳体全部进行考虑)受力计算结果统计如表1所示。由表1可知，增加破浪板使得液体在x方向上对罐体的冲击力明显降低。

表1 LPG储罐整体受力计算结果统计 105 N

无/有破浪板的LPG储罐压强计算结果如表2所示。由表2可知，增加破浪板能够减小压强波动幅度，降低罐体受到的最大压强，同时提高罐体的最小压强，从而提高结构安全裕量。

表2 不同时间LPG储罐压强计算结果统计 Pa

7 结 论

使用CFD对FPSO上的大型LPG储罐内的破浪板进行数值模拟，并就控制方程和边界条件进行有效性验证，建立六面体与四面体网格混合划分模型，通过CFD的动网格功能模拟船体晃动，结果表明：

(1) 选取的数值计算模型与试验结果吻合较好，结果是可信可行的。

(2) CFD模型计算结果能够较好地反映FPSO船体晃动对LPG大型储罐的液位和压力分布以及结构受力的影响。

(3) LPG储罐增加破浪板后，罐体内液体的晃动幅度减小，气液界面稳定，压力分布均匀且波动小，各部分受冲击力减小。

(4) 通过数值模拟可以得到LPG储罐的受力和压强等结果，为罐体的结构设计提供参考。