基于有限元的轴系回旋振动响应计算及试验

富琦晋，周瑞平，黄国兵，高子航

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

0 引 言

船舶推进轴系回旋振动主要是由于轴系在运转时受到螺旋桨旋转时产生的不平衡力、不均匀伴流场流体力及螺旋桨偏心质量的质量力而产生的一种横向振动。国内外对于回旋振动响应研究，大多在求解轴系临界转速的基础上，基于传递矩阵法进行简化处理，仅仅获取轴系的振动位移，主要是从轴心轨迹上分析回旋振动的影响。关于回旋振动反映在轴承基座上点的振动加速度响应的研究更是鲜有。周飞云[1]通过传递矩阵法计算某轴系的共振转速，并进行实船测试。王苏等[2]通过ANSYS计算舰船轴系的临界转速。马召召等[3]通过命令流计算喷水推进轴系的固有频率并绘制涡动振型。FIROUZI等[4]研究轴径和刚度对回旋振动固有频率的影响大小。LEE[5]计算50 000 t油船的回旋振动共振转速与弯曲应力，并通过应变仪进行实船测试完成验证。周凌波等[6-7]阐述回旋振动的激振力和影响因素及螺旋桨受横向单位激励力时回旋振动对艉部船体结构的激励特性。李小军等[8]研究尾轴承刚度对回旋振动的影响，并计算在幅值一定的横向力下螺旋桨与轴承节点处的位移响应，但其只研究不平衡力的横向分量且未考虑随转速的幅值变化。

目前，由于推进轴系的转速较低，在进行回旋振动固有特性的研究上往往忽略其与转速之间的关系，但实际上推进轴系的回旋振动是轴系的涡动，为更好地利用系统仿真方法进行回旋振动特性及相应研究，基于转子动力学中的概念，以涡动频率表述回旋振动频率随轴系转速的变化关系。同时，部分学者关于回旋振动响应的计算没有考虑旋转不平衡激励力是存在两个方向的分量且幅值随转速而变化的频域力，将其简化成单向且幅值一定的一般激励力，且一般只研究至螺旋桨或轴承所在节点处的响应值，而针对轴承及基座上点的响应计算较少，也未见验证其正确性的试验。

以某推进轴系台架为例，基于Workbench软件提出完整的回旋振动涡动频率及其响应计算方法，将频域响应力加在轴承支承中心，计算在额定工况下轴承基座上点的加速度响应，并设计振动试验，实测验证该方法的正确性。

1 涡动频率及振型

1.1 理论基础

转子动力学中考虑转动效应的结构动力方程为

(1)

转子动力学理论认为固有频率是结构的固有特性，只与结构自身刚度、质量分布有关。结构在转动时的振动频率称为涡动频率。当转速为零时涡动频率与固有频率相等。当转速不为零时，因回转效应的影响，转动结构的涡动频率随转速变化而改变，正进动 (Forward Whirling，FW) 频率随转速的增加而增加，逆进动 (Backward Whirling，BW) 频率则随转速的增加而减小。

1.2 台架有限元模型建立

图1为进行理论建模与试验研究的某推进轴系模拟台架，由模拟加载装置、配重盘、后尾轴承、前尾轴承、推力轴承、高弹性联轴器、减速齿轮箱及推进电机组成。

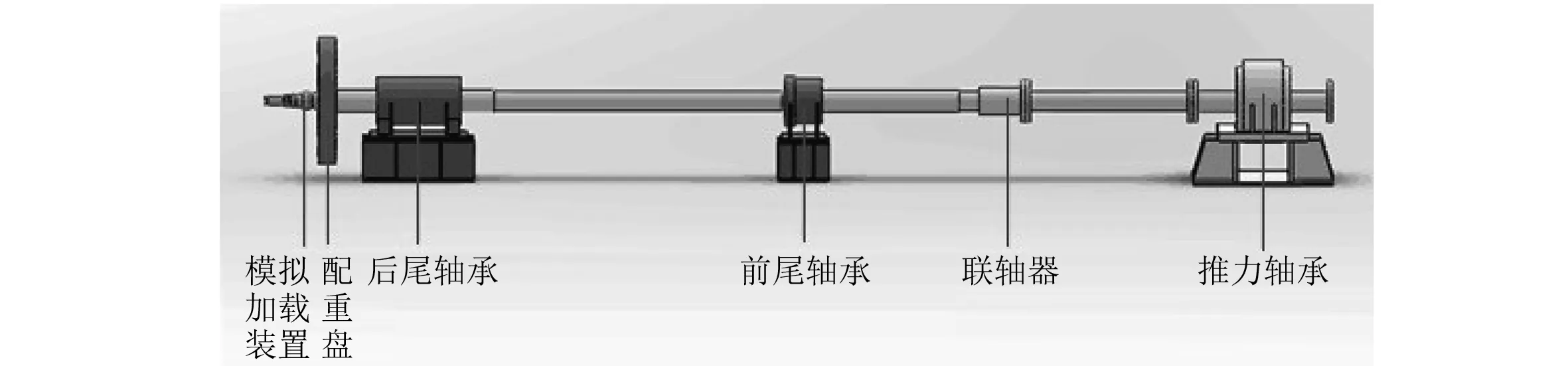
注：高弹性联轴器、减速齿轮箱、推进电机在图中省略图1 轴系台架布置

针对所研究的轴系台架，采用Workbench对轴系台架采取梁单元和实体单元两种建模方法，在求解回旋振动涡动频率时采用梁单元模型，在计算回转不平衡力激励对轴承基座的谐响应时需要求解轴承基座上点的响应值，因此通过SolidWorks对轴系台架进行实体建模。

1.3 涡动频率计算

转动结构部件的结构动力学分析需要考虑惯性效应的影响，即回旋振动的陀螺效应。在计算时打开阻尼效应和科里奥利效应。在后尾轴承、前尾轴承、推力轴承所在节点建立弹簧单元并设置刚度为1×106N/mm、1×107N/mm、1×107N/mm；赋予轴系转速并约束轴向平动及转动自由度去除刚体模态，在配重盘所在节点添加质量点并赋予质量4 800 kg、附水极惯性矩Jp为1 978 kg·m2、径惯性矩Jd为989 kg·m2。将末端节点的边界条件设置为简支，代表模型末端简化到高弹性联轴器处，如图2所示。

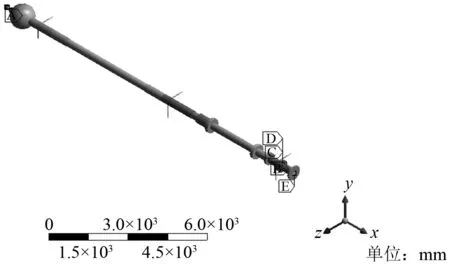
注： A为点质量； B为转速：0 r/min； C为位移； D为固定转动： 0°； E为简支4：0 mm图2 边界条件设置示例

在后处理模块添加“Total Deformation”以查看每一阶模态振型，插入“Campbell Diagram”以查看坎贝尔图并求解涡动频率和临界转速，如图3所示。坎贝尔图是描述涡动频率随转速不同而变化的图形。图3中斜率为1，代表1次回旋振动。当斜率为桨叶数时，代表叶频次回旋振动。斜线与涡动频率曲线的交点用三角标出，代表一、二、三阶1次回旋的BW与FW的临界转速值。坎贝尔曲线中转速为0时对应的3个频率点即为横向振动的前三阶固有频率。每1个临界转速对应1个涡动频率，在数值上涡动频率的值为其对应的临界转速除以60，单位为Hz。在坎贝尔图上的几何含义为临界转速点对应的y坐标值。

舰船推进轴系最高转速一般在300 r/min以下，如果横坐标按运行转速范围设置，坎贝尔图有时会变得不易观察。某阶模态的回转效应影响比较显著会使FW、BW频率曲线分离较大，增加转速可能会使其与其他阶的涡动频率曲线交叉从而影响结果。此时主要采取两种解决办法：(1)增加载荷步的数目，即增加求解坎贝尔图的转速点，在载荷步数增加时坎贝尔图会更趋于一条光滑的曲线；

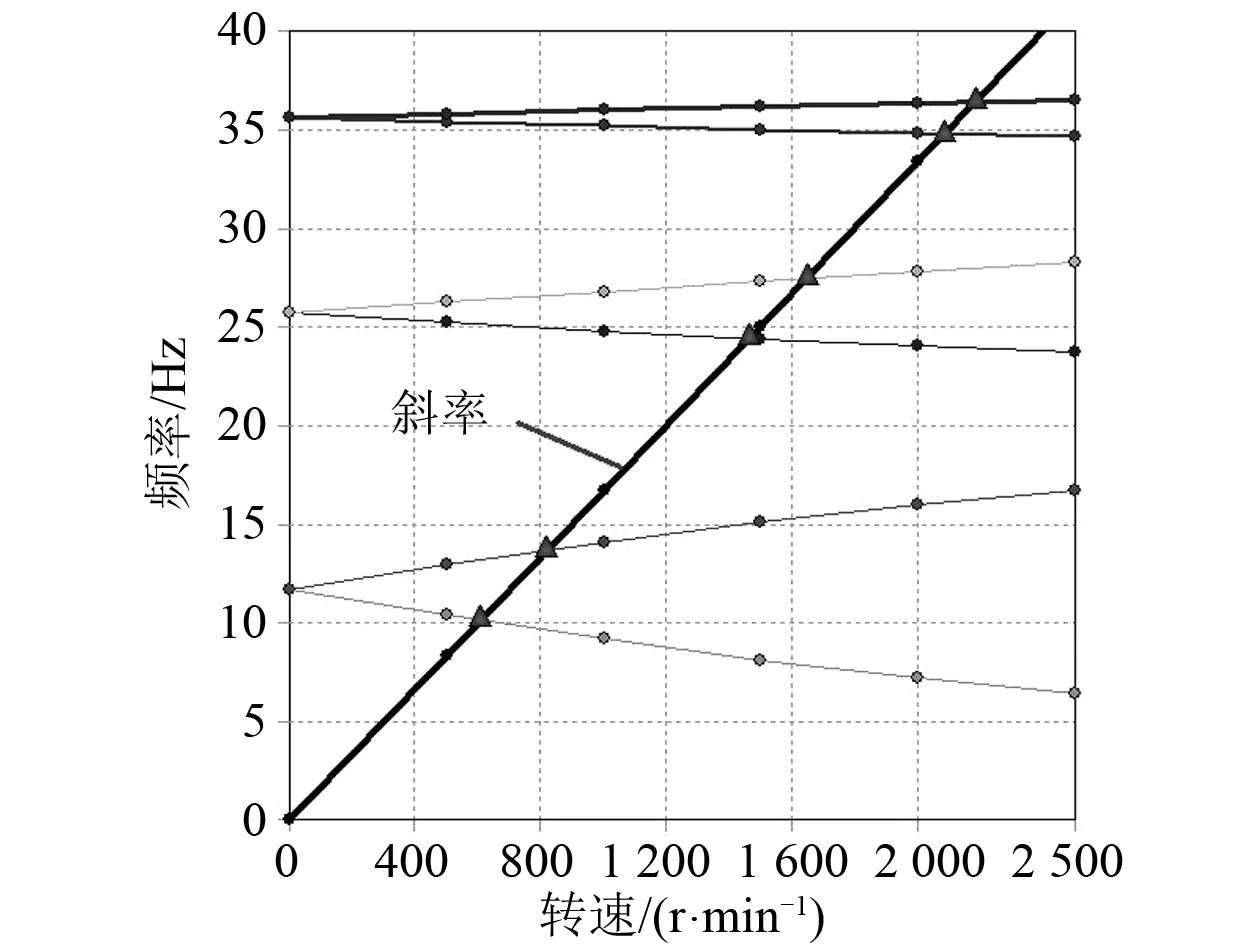
图3 坎贝尔涡动曲线图

(2)减小分析的转速，在转速减小时，正逆涡动频率差值减小，不易产生频率曲线交叉现象。

由于本轴系通过配重盘模拟螺旋桨，只存在轴频而不存在叶频次，因此，在仿真计算中只考虑1次正回旋(h=1)与1次逆回旋(h=-1)。将有限元回旋振动计算所得涡动频率与传统传递矩阵法计算所得固有频率结果进行对比，如表1所示。

表1 固有频率结果对比

由表1可看出：有限元法计算所得频率与传统传递矩阵法所得固有频率误差小于1%，表明边界条件设置及有限元计算是准确的。

得到涡动频率后选择“User Defined Result”对涡动振型进行绘制后处理。目前以传递矩阵法为基础进行振型的推算时，由于累加误差的影响，难以获取满意的振动形态。如果考虑实际轴承支承的各向异性，传递矩阵法振型绘制会更加麻烦，且准确性较差。通过有限元法可在“Tabular Data”中获得轴上每个节点的振动幅值，得到较为精确的轴系挠度曲线，即正逆回旋的各阶振型。图4为正回旋振型。由图4可知：不同阶回旋振动振型不同；由于回转效应，正回旋与逆回旋的涡动频率不同，但同一阶正回旋和逆回旋的振型与幅值都完全相同，只是方向不同而已。

图4 正回旋振型

2 回旋不平衡力响应及轴承座响应计算

2.1 激励力

关于推进轴系回旋振动的激励力，特别是对于潜艇推进轴系，其激励主要来自螺旋桨水动力及旋转过程中产生的不平衡力等，关于螺旋桨激励的计算国内外文献已有充分的研究。为模拟螺旋桨水动力的影响，试验台架一般设计有轴向及横向加载装置。在试验轴系台架正常运转工况下，电机激振力及偏心重力引起的二次激振力的影响较小，可将其忽略。由于试验条件所限，研究中只考虑模拟螺旋桨的配重盘旋转时产生的不平衡离心力。配重盘质量较大且悬臂支承，因此在旋转时由于偏心质量的存在产生旋转不平衡力F0。针对单一激励力，研究回旋振动不平衡力响应的计算方法：

F0=meω2=meΩ2

(2)

式中：m为偏心质量，kg；e为偏心质量中心到转轴的距离，m；ω为结构转速，rad/s；Ω为激励圆频率，rad/s。

由式(2)可知：旋转不平衡激励力区别于大小不随转速而变化的一般激励力，其幅值与转速有关。在激励范围内，不平衡力是一个幅值随激励频率(转速)变化的频域力。

对于推进轴系来说，其激励与转轴的结构转速不一定是同步的。在船舶运行时，流体的激励频率为叶频，螺旋桨偏心产生的重力激励频率为两倍轴频，质量偏心旋转产生的不平衡激励频率为轴频。因此，在每个激励频率下采用结构转速来计算回转效应。结构转速ω计算式为

ω=Ω/s=2πf/s

(3)

式中：f为激励频率，Hz；s为激励圆频率Ω与结构转速ω之比。在Workbench的“Rotating Force”中，“Synchronous Ratio”即为s。

在轴系的转速方向定义为轴向(x向)时，其激励力F的相位滞后角为α，作用在垂直转轴的平面内。旋转不平衡激励力的大小与方向都随转动而变化，但其方向始终为运动轨迹的切线方向，且幅值是一定的。因此，旋转不平衡激励力可分解成幅值相等的横向、垂向两个简谐力，即

Fy=F0cos(Ωt-α)

(4)

Fz=F0sin(Ωt-α)

(5)

式中：Fy、Fz分别为横向、垂向的简谐激励力；Ωt、α分别为激励力的相位角与相位滞后角。

图5为一般激振力分解示例。

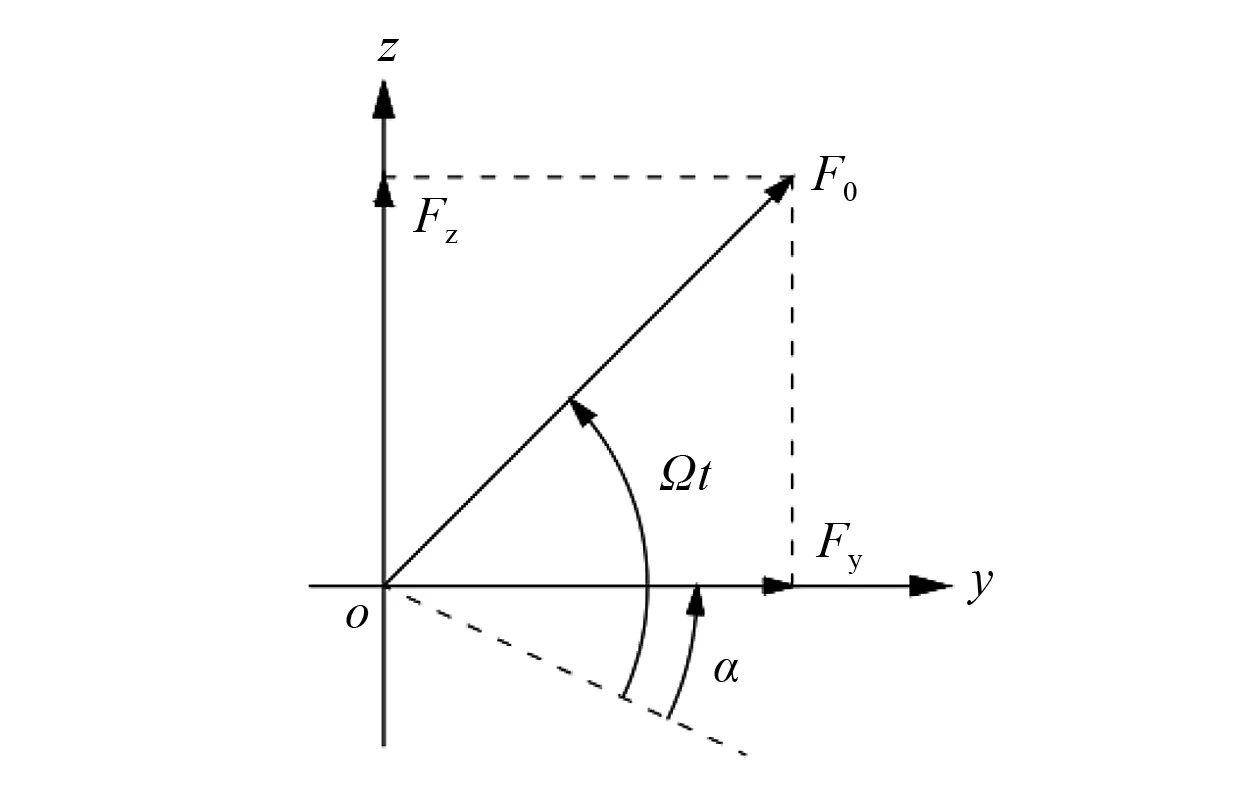
图5 一般激振力分解示例

对于质量偏心旋转产生的不平衡激励力而言，其激励频率与结构转速相等，相位滞后角α为0，将激励用复数形式表示可得

Fy=F0ej Ω t

(6)

Fz=-jF0ej Ω t

(7)

即y向、z向激励力幅值相等且相位角相差90°。

2.2 回旋振动响应计算

在谐响应分析中需要考虑系统阻尼。根据实测和相关资料，钢结构的阻尼比一般在0.01～0.02，将结构阻尼系数设置为0.02。滑动轴承阻尼通常为103～105N，因此在轴承对应的弹簧单元中设置轴承阻尼值为105N。

在Workbench的“Rotating Force”中，“Synchronous Ratio”定义激励频率与结构转速的比值，即谐响应激励频率与结构转动频率是否同步。其可对谐响应的每个频率步通过激励频率更新转速，在该项缺省时则定义为不平衡激励，否则为不随转速变化的一般转动谐波激励力。据此，将“Ratio”项设置为空，并输入质量m、不平衡质量旋转半径r，即不平衡力F0=mr。ANSYS会自动在每一频率步将转速的平方项相乘进行运算求解。采用这种定义方式可避免激励力手动计算及表格加载。在配重盘所在节点设置m=45 kg，r=0.03 m，可得旋转不平衡力F0=1.35 kg。

在实测中轴承所在节点位移响应无法测量，因此在后尾轴承前端10 mm的轴上设置1个节点，并计算其位移响应，方便与试验数据进行对比。在“Analysis Setting”中将最小频率设置为1.33 Hz，最大频率设置为3.33 Hz，迭代次数设置为13。求解测点在80～200 r/min稳定工作转速下的垂直和水平方向振动位移响应值。

由响应仿真计算可得：在激励频率为3.33 Hz时，即轴系台架在200 r/min额定转速工况下运转时，轴上测点的横向与垂向振动位移响应值均为0.010 02 mm。由于激励力是y、z方向幅值相等，且为相位角相差90°的旋转不平衡力，因此横向、垂向位移响应幅值相等且横向响应相位角比垂向滞后90°。

2.3 轴承基座响应计算

求得轴上测点响应后，计算在额定工况下不平衡力激励时轴承座上测点的加速度响应。通过插入探针获取后尾轴承处弹簧单元的响应变形量和频域响应力，即为后尾轴承受到的频域力。在后尾轴承支承中心施加此频域力并再次进行谐响应计算，求解轴承基座处测点的加速度响应。新建两个参考坐标系，切分出支承中心所在截面和下轴瓦的受力面，并在轴承顶端、轴承两层基座上建立与试验相同的3个测点。在振动试验中后尾轴承基座的测点布置如图6所示。

在进行后尾轴承的谐响应分析时，激励为计算回旋振动响应所得到的频域力。其中，频域激励力的y、z向幅值是相等的，且z向的相位角比y向滞后90°。考虑到轴承真实受力情况仅为下轴瓦约30°～45°部分受力，而非整个轴承轴瓦面均受力，因此选取受力面时只取下轴瓦面的一部分。

图6 后尾轴承基座测点布置

轴承的真实受力位置，即支承中心所在位置，并不在轴向中心1/2处。针对后尾轴承，通常轴向约1/3处才是其真实支承中心所在截面，因此轴承激励力不能直接通过“Force”进行简单的加载，而是需要通过“Remote Force”指定其真实受力点确定支承中心所在位置，再将激励力耦合至下轴瓦面，并通过力的平移定理将力和力矩传递到轴承的下轴瓦面上。将远端力的施力点选在轴向1/3处所在截面的中心。激励的施力点与下轴瓦受力面的耦合、频域激励力加载情况如图7所示。

此时激励力的加载，不仅考虑轴承真实受力面情况，而且考虑轴承支承点位置选取对结果的影响，更符合实际情况。由于实体单元的响应计算较复杂，网格密度较小，所需计算时间较长，并且考虑到测试工况的稳定程度会对结果产生影响，因此选取轴系试验台架200 r/min的额定转速工况进行仿真计算与对比。将计算频率设置为3.33 Hz，在后处理模块查看3个测点y向、z向的响应加速度。通过仿真计算所得，在200 r/min转速工况下测点1的垂向、横向加速度响应值分别为0.129 20 m/s2、0.213 89 m/s2，测点2分别为0.236 31 m/s2、0.195 45 m/s2，测点3分别为0.107 18 m/s2、0.073 26 m/s2。

3 试验与仿真数据分析

3.1 轴系振动测试系统

在台架轴系回旋振动测试时，采用国内外回旋振动测量通用的非接触式法，采用多功能数据采集仪结合电涡流传感器进行测量。振动测点布置在尾承前端10 cm处。在轴承及其支座振动测试中，采

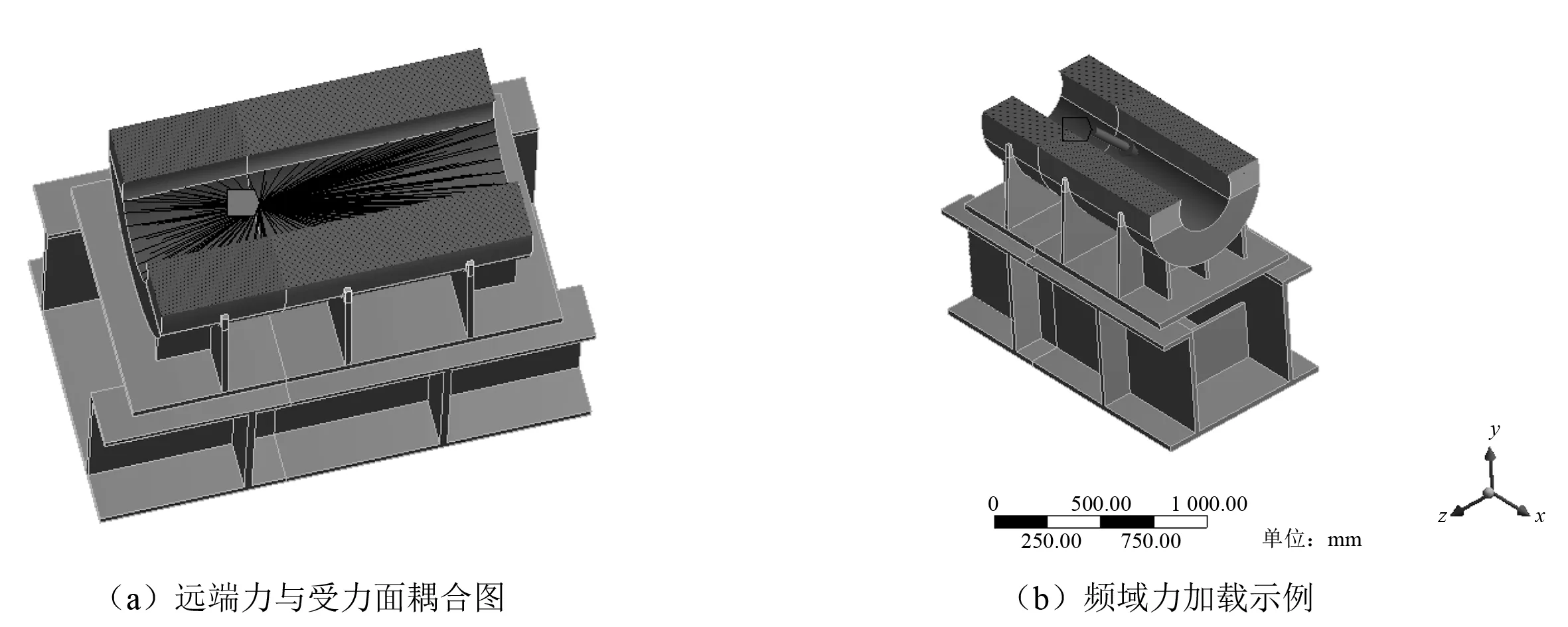
图7 远端力耦合及频域力加载情况

用加速度传感器测量轴承及其支座的振动加速度信号，通过信号采集仪进行加速度信号采集，并连接至测试电脑。振动测试传感器型号及参数如表2所示。振动测试系统如图8所示。

表2 传感器型号及参数

图8 振动测试系统

3.2 位移响应测试结果及对比分析

在台架轴系位移响应测试时，将电机转速从80 r/min上升至额定转速200 r/min，通过电涡流传感器记录轴上测点的振动位移，将测试结果与第2.2节中仿真计算所得同一点的振动位移随转速变化结果进行绘制，如图9所示。图9中虚线为轴上测点的振动位移，实线为有限元仿真计算结果。

由图9可看出：轴的振动位移仿真分析结果与实测的趋势是一致的，但实测轴的振动位移随转速的变化存在一定的波动，而仿真计算相对比较光滑。这主要是由于电涡流传感器的测试结果是相对值，且轴运转时的不稳定性会直接导致轴的振动位移存在波动。同时，在稳定运转工况200 r/min下，后尾轴承前端10 mm轴上测点的振动位移仿真计算结果为0.010 02 mm，实测幅值为0.011 07 mm，二者相差较小，说明仿真计算模型、边界条件的设置及加载方法是正确的。

3.3 轴承加速度响应测试结果及对比分析

在轴承座加速度响应测试时，将电机转速设置为额定转速200 r/min，通过轴承及基座上的加速

图9 测点横向振动响应曲线图

度传感器记录轴承振动加速度值。将第2.3节中仿真计算所得后尾轴承上3个振动测点的加速度响应值与实测值进行对比，如表3所示。

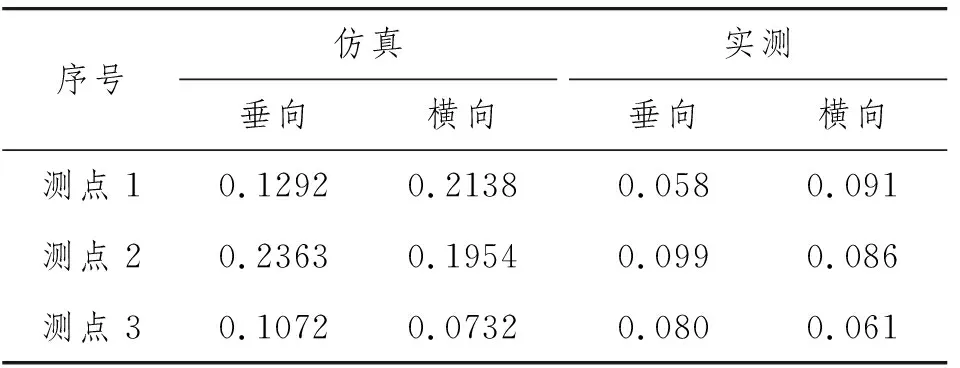
表3 轴承振动结果对比表 m·s-2

由表3可看出：

(1) 轴承座横向振动响应加速度为轴承顶部最大(测点1)，轴承座第1层次之(测点2)，且轴承顶部与第1层基座横向响应值比较接近，均大于轴承座底部(测点3)。此相对关系与实测值一致。

(2) 轴承座垂向振动响应加速度为轴承座第1层最大(测点2)，轴承顶部次之(测点1)，轴承座第2层最小(测点3)，但三者在同一数量级，其中测点1、测点3仿真值均略大于实测值。对于测点2，其实测与仿真的振动响应加速度均最大。

(3) 轴承座同一测点的横向及垂向加速度响应仿真与实测完全一致。轴承顶部的横向响应值大于垂向响应值(测点1)，而轴承基座第1层和第2层的垂向响应值均大于横向响应值(测点2、测点3)。

(4) 对比仿真结果与试验结果可知：仿真与实测在数值上存在一定的差异，但其结果都在同一数量级，且仿真与实测除垂向的个别测点大小关系存在差异外，轴承振动响应加速度的仿真与实测结果在大小及相对关系上都是匹配的。分析原因，可能是仿真中的激励力理想化为螺旋桨模拟配重盘的不平衡力，忽略其他激励因素的影响，如齿轮啮合、轴与轴承的摩擦、电机运转的不平稳性等。

4 结 论

(1) 通过有限元法仿真所得涡动频率与传统传递矩阵法所得固有频率相对偏差小于1%，且较传统传递矩阵法易于获取轴系的横向振动模态，可较好地满足推进轴系回旋振动模态的计算。

(2) 由于回转效应的影响，轴系回旋振动FW与BW的涡动频率虽不同，但同阶FW与BW的振型与幅值完全相同，只是方向不同。

(3) 通过所给边界条件的设置方法、载荷加载处理等，方便地实现轴系回旋振动响应计算，且通过实测验证响应分析的正确性，其方法可为轴系设计中回旋振动的响应预报提供理论支撑。

(4) 通过对轴承座三维及有限元的精确建模，将轴系振动响应等效为作用于轴承座上的激励力，对轴承座振动响应进行分析，实测表明：轴承基座上振动响应的仿真计算与实测结果趋势一致。