基于社会力模型的邮船舱段疏散滞后性分析

刘经京，姚汝林，董小伟，余 龙*

(1.上海交通大学 a.海洋工程国家重点实验室；b.船舶海洋与建筑工程学院；c.高新船舶与深海开发装备协同创新中心，上海 200240；2.招商局邮轮制造有限公司，江苏 南通 226116；3.招商局重工(江苏)有限公司，江苏 南通 226116)

0 引 言

GALEA等[1]在3种不同类型的客船上进行疏散演练，收集疏散响应时间、到达集合点时刻和人员疏散路径等数据，并与模拟结果进行比较。PITANA等[2]利用离散事件模拟(Discrete Event Simulation,DES)方法模拟海啸袭击后的旅客疏散过程，预报疏散所需时间。ROH等[3]提出基于单元的疏散仿真模型，模型在统一网格单元中划分空间，每个单元中实现离散事件和离散时间的组合，通过与国际海事组织(IMO)规定的11项试验对比，验证该方法在模拟船舶提前疏散过程方面的适用性。BLES等[4]讨论船舶倾斜和运动对人员行走速度的影响。

廖守衡等[5]介绍IMO关于客船疏散的相关规则，讨论船舶疏散仿真与陆地疏散差异，分析3种典型船舶疏散仿真工具的未来发展前景。徐澄[6]基于元胞自动机理论深入研究客船在甲板布置时需要考虑的布局规则和走廊、门的布置等。郭琳[7]基于一艘大型客船的疏散数据对IMO指南进行验证，得出IMO指南更好应用于中国客船的调整方案。倪宝成等[8]结合改进社会力模型与智能体建模技术，提出一种考虑逆行避让行为和穿戴救生衣行为的船舶疏散仿真模型。

上述文献对于邮船上乘客听到警报从舱室进入走廊这一段过程的人员行动规律研究较少，并假设所有乘客听到警报后都会立刻开始疏散，但现实中未经训练的乘客一般会经历一段反应时间后才能开始疏散，与此同时，走廊内往往涌来从其他方向疏散的乘客，若此时还在船舱中的乘客由相对密闭的客舱进入狭窄走廊，将很容易引发拥挤、碰撞、踩踏等事故。针对这些问题，在HELBING等[9]提出的社会力模型基础上，引入船体倾斜造成的人员速度衰减影响，并改进速度驱动力项以消除舱门狭窄造成的不合理阻塞，建立符合特定情景的疏散模型。

1 社会力模型简介

1.1 基本原理

在HELBING等提出的社会力模型中，人员个体i被假定为具有一定质量mi和半径ri的粒子。乘客在移动过程中受到诸多力的作用，包括乘客自身驱动力、乘客之间的相互作用力和乘客与墙壁等障碍物之间的相互作用力，数学形式为

(1)

式中：vi为乘客i当前速度；t为时间；fd,i(t)为乘客自身驱动力；fij为乘客之间的相互作用力；fiW为乘客与墙壁等障碍物之间的相互作用力。

乘客自身驱动力表示个体期望在一段特征时间内将当前实际速度改变至期望速度，数学形式为

(2)

式中：v0,i(t)e0,i(t)为期望速度；vi(t)为当前实际速度；τi为特征时间。

乘客之间的相互作用力包括两名乘客i和j在相互接近过程中产生的心理排斥力、发生实际接触后的挤压力和摩擦力，数学形式为

fij={Aiexp[(rij-dij)/Bi]+kg(rij-dij)}nij+

κg(rij-dij)Δvt,ijtij

(3)

式中：Ai和Bi为常数，分别取2 000 N和0.08 m；rij=ri+rj，为两名乘客粒子半径之和；dij=‖ri-rj‖，为两名乘客粒子中心间距；k为乘客挤压弹性系数，取1.2×105kg/s2；nij为两名乘客粒子连线方向；κ为乘客滑动摩擦系数，取2.4×105kg/(ms)；在乘客之间没有发生接触时，函数g(x)取0，否则取x；Δvt,ij=(vj-vi)·tij，tij为两名乘客切向方向。

乘客与墙壁等障碍物之间的相互作用力的数学形式为

fiW={Aiexp[ri-diW)/Bi]+kg(ri-diW)}niW-

κg(ri-diW)(vi·tiW)tiW

(4)

式中：diW为乘客与墙壁之间的距离；niW为乘客粒子与墙壁粒子连线的方向；tiW为乘客粒子与墙壁粒子之间切向方向。

1.2 模型改进

有研究[10]表明，在船舶上，特别是在大型客船上，除疏散通道结构、人员自身属性外，船体浮摇状态对人员疏散也有着重要影响。在船体处于倾斜状态时，人员为克服重力作用会调整运动姿态而导致运动速度下降。根据德国提交给IMO的报告可确定横倾和纵倾状态下人员期望速度的缩减比，即

(5)

(6)

式(5)和式(6)中：Λ1为横倾引发的速度衰减；φ1为横倾角；Λ2为纵倾引发的速度衰减；φ2为纵倾角。

邮船客舱舱门狭小，且往往面对较为窄小的走廊。在走廊内的人员密度较大时，如果使用原模型的相互作用公式，就会出现舱内乘客因为社会力作用而被一直堵在门内的不合理现象。在现实疏散过程中，舱室内乘客被堵住一段时间后会增强离开舱室的意愿并强行挤入走廊，社会力引起的排斥作用降低。对式(3)进行修正，得

fij={ψ(τi)Aiexp[(rij-dij)/Bi]+

kg(rij-dij)}nij+κg(rij-dij)Δvt,ijtij

(7)

(8)

式中：ψ(τi)为对心理排斥力的修正系数，τi为乘客速度处于0.30 m/s以下的连续累计时间。

2 计算模型

2.1 确定计算舱段单元

以一艘中型邮船为例，其上层舱室建筑呈对称布置，每侧各分布32个上下铺4人标准舱室(7.47 m×3.5 m)，如图1所示。船体中间区域为食品贮藏室和配电供给室，默认为不可穿越地区。有序高效的疏散是听到警报后各舱室的乘客向离自己最近的出口按照从近到远的顺序依次撤离。但是现实中没有经过训练的乘客往往无法做到听到警报后立刻疏散，而其中相对危险的情况就是乘客在看到人员来流已经疏散至所在舱室的舱门处才意识到撤离的必要性。

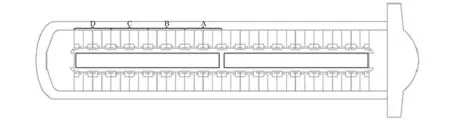
图1 舱室布置

基于理想化的标准情景作出如下假设：

(1) 所有乘客默认为成年男性，期望速度取IMO海上安全委员会(MSC)第1033号通函中所列密度为零时人员的初始速度1.20 m/s。

(2) 分析中不考虑相识人员聚集效应，疏散开始后所有人员只向离自己最近的路口运动。

(3) 分析中不考虑人员摔倒等意外因素。

如果将全部舱室建模，计算量会随着乘客数量的增多而急剧增大，计算效率大幅下降。考虑到该邮船的舱室布置简单对称，提出分段分析的方法，即将4节舱室作为1个舱段计算单元。每次计算只建立1个单元的模型，在初始时刻每个舱室4名乘客随机分布在房间任何角落，如图2所示。分别模拟发生滞后时图1中A、B、C、D舱段的疏散过程，每次的仿真计算结果作为下次计算的初始条件。

2.2 疏散情景仿真

2.2.1 情景1：走廊右侧无人员来流

计算单元设定图1中的A舱段，计算过程不考虑通道内右侧舱室疏散的人员来流，舱内乘客不用考虑避让而自由进入走廊。图3为疏散开始后6.00～10.00 s的人员分布情况，圆形散点表示舱内乘客。由图3可看出：疏散开始后0～10.00 s，所有乘客向自身所在舱室的舱门处移动，由于舱内人数较少且与舱门之间距离不一，乘客可做到快速有序地通过舱门进入走廊而不发生拥堵。10.00 s之后，乘客在进入走廊后进行短暂调整，基本保持一字队形快速前往出口处，疏散时间为21.33 s。

图2 舱段计算单元

2.2.2 情景2：滞后1个舱段

计算单元设定图1中的B舱段，且假定A舱段已经有一半疏散人员通过人员来流入口进入该舱段的走廊，人员来流的数量和速度根据情景1中乘客离开出口处状态确定。图4为0～15.00 s的人员分布情况，其中方形散点表示走廊右侧人员来流。与图3比较可看出：为避让走廊内的人员来流，舱内乘客在通过舱门时出现短暂的排队现象，之后跨过舱门的舱室乘客与右侧来流会合并成两排队形前进，但是整个过程没有发生明显的拥堵。

图3 情景1疏散示例

2.2.3 情景3：滞后2个舱段

计算单元设定图1中的C舱段，且假定A、B舱段都发生滞后，已经有一半疏散人员通过人员来流入口进入该舱段的走廊，人员来流的数量和速度根据情景2中乘客离开出口处状态确定。图5为0～27.00 s的人员分布情况。与图3、图4比较可看出：在计算初始时刻走廊内的人员来流就呈现双排前进模式，所以3号和4号舱室内的乘客很难寻找到人员来流中的空隙进入走廊，必须通过插队实现出舱。图5(b)至图5(e)展示插队过程：首先舱内乘客在出舱时会将走廊内连续并排的人员来流截成2～3段，一段时间后走廊内出现若干空白段，这时舱内乘客迅速插入走廊，然后队伍继续加速前进追赶空白段前面的疏散人员，直至走廊内的人员来流密度下降到下一名乘客可出舱的程度。插队行为虽然可让一名乘客走出舱室，但是会截断走廊内的人员来流并造成更严重的拥堵，从而阻止下一名乘客走出舱室。在实际疏散中，插队出舱行为很可能引发踩踏等事故。

图4 情景2疏散示例

2.2.4 情景4：滞后3个舱段

计算单元设定图1中的D舱段，且假定A、B、C舱段都发生滞后，已经有一半疏散人员通过人员来流入口进入计算舱段的走廊，人员来流的数量和速度根据情景3中乘客离开出口处状态确定。图6为0～40.00 s的人员分布情况。与图5比较可看出：类似于情景3，情景4中所有舱室乘客出舱均需要经过第2.2.3节中描述的插队过程，并且由于走廊内的人员来流密度更高，每次完成插队后需要更多的乘客通过出口才能使密度降低到足够下一名乘客出舱的程度，疏散过程耗费在等待上面的时间大幅加长。

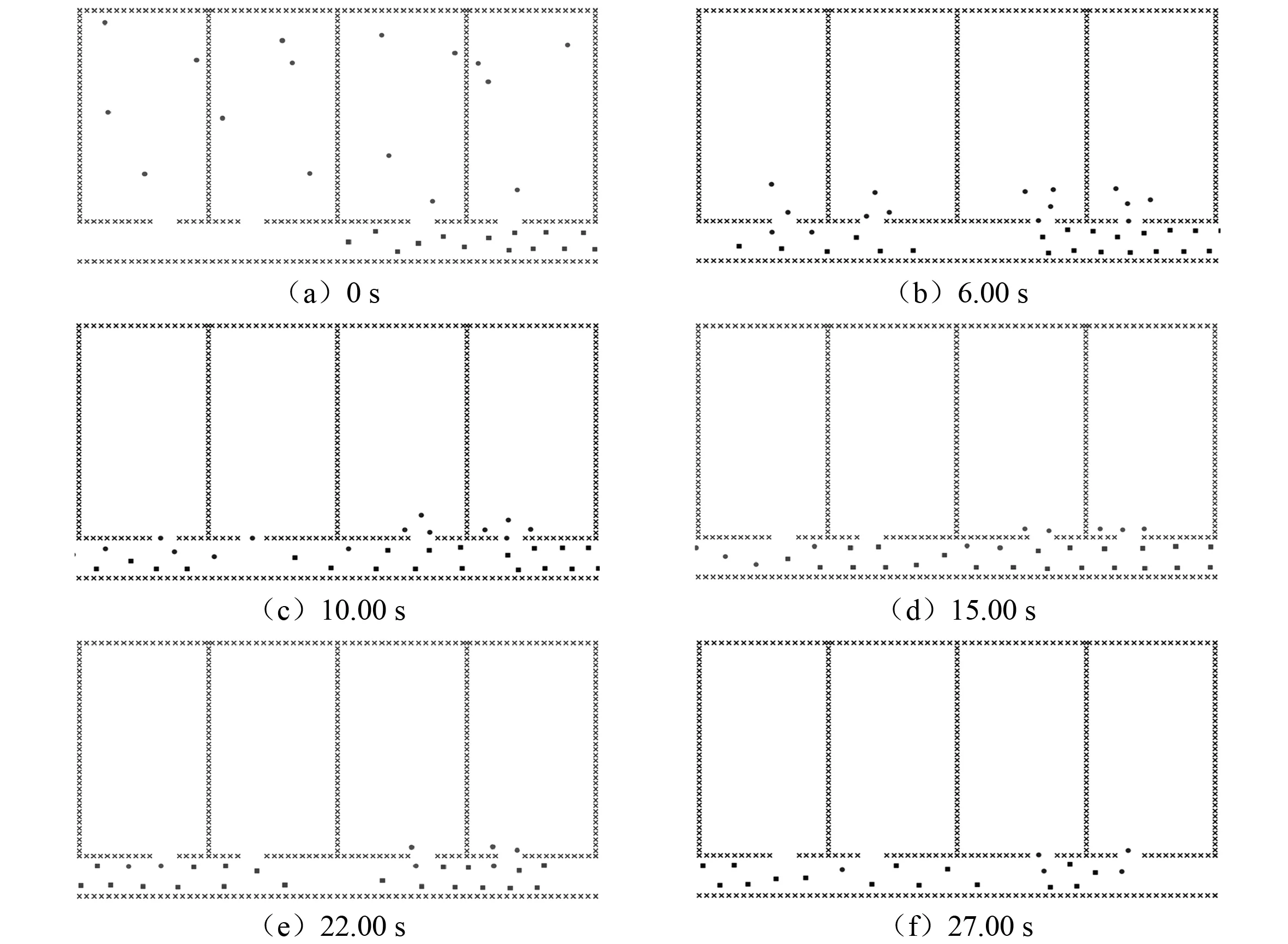
图5 情景3疏散示例

图6 情景4疏散示例

2.3 疏散仿真计算

2.3.1 单一舱段疏散计算

选用每个情景的出口平均速度、疏散时间、人均疏散时间、最大拥堵时间和人均拥堵时间等参量作为评价指标，如表1所示。

表1 疏散评价指标

人均疏散时间和人均拥堵时间定义如下：

(1) 人均疏散时间t为舱室内所有人员完成疏散全过程所花费的累计时间平均值，数学形式为

(9)

式中：ti为乘客i通过出口的时间；n为总人数。

(2) 人均拥堵时间tk为舱室内所有人员在低于0.30 m/s的运动速度下运动累计时间平均值，数学形式为

(10)

式中：tki为乘客i处于拥堵状态的时间。

由表1可看出：疏散没有发生滞后时人员可在走廊内形成单线队形并以较快的速度(0.96 m/s)进行疏散；一旦走廊内存在其他舱室的人员来流，疏散就会形成两队队形，疏散平均速度降至0.60 m/s附近；走廊内的人员来流越密集，疏散时间、人均疏散时间、最大拥堵时间和人均拥堵时间等指标越大。人均拥堵时间与人均疏散时间的差值分别为13.31 s、13.07 s、13.95 s、14.59 s，人均有效疏散时间相差不大。人均拥堵时间与人均疏散时间的比值分别2.78%、17.44%、38.84%、57.80%，特别是在情景4中，舱内大多数乘客几乎把一半的疏散时间耗费在等待中，真正有效的疏散时间不到50%，疏散时间几乎是情景1的3倍，疏散效率大幅降低。因此，在现实生活中应加强对乘客的紧急疏散演练，做到听到警报后所有舱室同时开始疏散，以避免某些舱段疏散滞后现象特别是情景4的出现。

2.3.2 全舱段疏散计算

以该邮船A、B、C、D舱段为例，进行全舱段疏散计算。如果所有舱室可同时有序疏散，则对A、B、C、D舱段选用情景1的结果研究乘客出舱的疏散效率。如果B舱段发生疏散滞后，则对A、C、D舱段选用情景1的结果研究乘客出舱的疏散效率，对B舱段选用情景2的结果。如果B、C舱段发生疏散滞后，则对A、D舱段选用情景1的结果研究乘客出舱的疏散效率，对B舱段选用情景2的结果，对C舱段选用情景3的结果。最危险的情况就是B、C、D舱段全部发生疏散滞后，即情景4。该邮船全舱段疏散总时间如表2所示，可看出：发生严重滞后的疏散总时间2倍于无滞后的疏散总时间。

表2 全舱段疏散总时间 s

3 结 论

计算结果显示，在有2节以上舱段出现滞后现象时会出现非常严重的拥堵现象，舱内乘客只能通过插队完成出舱疏散，疏散总时间大幅增加，严重影响疏散效率并增加安全隐患。因此，中型或大型邮船在日常运营过程中应反复加强乘客疏散演练工作，使乘客听到警报后立即有序疏散。所提出的分段分析、计算的方法对其他单主干道布置或不闭合双主干道布置客船的流线设计也具有通用性和适用性。