基于C#与MATLAB混合编程的船舶压载水仿真系统

周 佳，刘夕全，宋 磊*，孙承猛

(1.山东交通学院 船舶与轮机工程学院，山东 威海 264209；2.山东海洋工程装备有限公司，山东 青岛 266555)

0 引 言

船舶压载水系统根据船舶营运或作业的需要，对全船压载舱进行注水或排水，以调整船舶吃水、船体纵横倾角度和稳心高度，减小船体变形，以免引起过大的弯曲力矩与剪切力[1]。由于大型船舶的压载水舱数量众多，相应的调载方案也多，而方案的优劣往往对调载作业时间的长短、功耗的高低、船体受力情况的好坏、作业过程的安全与否等产生影响。在正式作业前，对船舶压载水调节过程进行仿真预演，可以保证作业过程的安全高效，也是培训船员进行压载水相关操作管理、提升操作水平的有效手段。

国内多所高校开展船舶压载水系统仿真研究。张鑫等[2]建立船舶压载水系统仿真模型，但仅对船舶压载过程进行模拟，对船舶在航状态的压载水调节并未作相关研究；肖民等[3]使用MINIS通用仿真支撑系统和InTouch组态软件为平台开发船舶压载水模拟训练系统，并加入自动调节功能，但该调节功能需要用户先制订控制逻辑，且不便修改。董恩春等[4]基于WebAccess组态软件建立船舶压载水仿真与监测系统，可实现远程监控和访问，但没有加入调载功能，而在仿真系统中加入自动调载功能，可优化调载方案，辅助操作人员制订合适的压载水调节方案；潘伟等[5]对全回转起重船压载水调节进行优化研究，可有效避免经验法可能导致的危险情况；魏伊[6]在201起重铺管船调载仿真中研究基于改进非劣分层遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ,NSGA-Ⅱ)的调载算法，为起重船的调载优化提供新思路；秦军超[7]在蓝鲸号起重船的调载仿真中应用基于多目标略减粒子群优化算法的调载算法，同样实现船舶压载水调节的优化。然而，这些仿真系统都是针对某特定船舶而设计的，不具备通用性。船员在使用仿真系统进行压载水操作训练时也只能针对某一艘船，有较大的局限性。若更换船型，则需对整个仿真软件重新进行设计，会大幅增加开发成本。因此，研究一套船舶压载水管网的参数化建模方法，开发具有通用性的船舶压载水仿真系统，并在系统中加入调载优化算法，能够实现调载方案的优化功能，从而辅助操作人员决策。

1 仿真系统总体设计

船舶压载水仿真系统包括软件界面、计算模块和数据库模块。系统开发采用C#、MATLAB和结构化查询语言(Structured Query Language,SQL)混合编程的方法。C#虽然具有强大的界面设计能力和优良的处理速度，但数值计算和曲线绘图能力不足，而MATLAB虽然拥有优秀的数值计算和曲线绘图能力，但界面设计过于简单。使用三者混合编程的方法，可实现优势互补，从而提高编程效率。系统的架构设计如图1所示。

(1) 基于C#的软件界面。为了使用户获得良好的操作体验，仿真系统使用C#开发软件界面。主界面采用多文档界面(Multiple Document Interface,MDI)窗体设计，集成参数化建模向导、工况管理、压载系统仿真与监控、数据信息查看与更新、调载参数设置等功能界面。

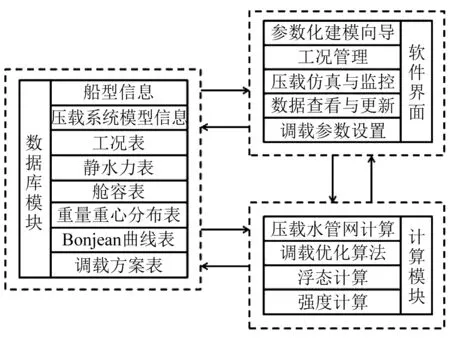
图1 系统架构设计

(2) 基于MATLAB的计算模块。仿真系统计算模块包括压载水管网计算、调载优化算法、浮态计算与强度计算。其中：压载水管网计算与管网仿真模型紧密相连，采用C#实现；调载优化算法、浮态计算与强度计算则是借助MATLAB在数值计算分析和曲线绘图方面的强大功能实现。

(3) 基于SQL的数据库模块。系统将船型信息、压载系统模型信息、工况表、静水力表、舱容表、重量重心分布表、邦戎曲线(Bonjean’s Curve)表、调载方案等相关数据均以数据表的形式存储，并可根据需要进行动态的添加、删除和更新，方便系统各功能间的调用，实现压载系统参数化建模和高效计算。

(4) 混合编程实现系统集成。C#与MATLAB采用.NET组件技术实现混合编程。将调载优化算法、浮态计算和强度计算部分编写成3个MATLAB函数，然后将这些函数做成动态链接库文件，C#可以直接调用特定的接口函数来实现各项计算功能，从而将软件的界面与计算集成为完整的仿真系统。

2 压载水管网参数化建模方法

船舶压载水系统主要由压载水泵、压载水管路、压载舱及有关阀件组成。根据实船压载水系统建立压载水管网模型是实现仿真系统各项功能的基础。

2.1 压载水管网计算数学模型

建立压载水管网计算数学模型是为了进行管网流量计算，其中水力计算是核心内容。通过有限元法建立压载水管网计算数学模型。将整个管网划分为若干个管元，管元的端部和管元之间的连接处均设为节点。压载水在管网中沿管线的纵向做一维流动，节点和管元的参数反应管网的压头降和流量分布[6]。

管元单元方程为

Qi=k·Δh

(1)

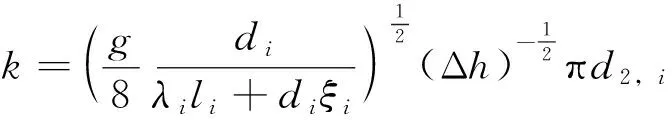
节点连续方程为

∑Qi=Ci

(2)

式中：Ci为节点净流量。

管网矩阵方程为

(3)

式(3)简写为KH=Q，其中：K矩阵与压载水管路网格形状有关，是管路网格的特征矩阵；H为管网节点的水头列向量；Q为管网节点流量列向量。

对式(3)进行矩阵分割并迭代求解，从而使建立的模型可实时计算出各段管路的流量和各压载舱的液位变化情况，模拟出压载泵和管路阀门的工作状态。

2.2 压载水管网参数化建模

由于管网模型是根据实船的压载水系统原理图建立的，所以以往的仿真系统一般都是针对某一特定船舶开发的，若更换船型或更改压载水系统，则管网数学模型需重新建立，仿真系统也需重新设计，由此带来较高的软件开发成本。所开发的仿真系统使用参数化建模的概念，将管路系统中的各项信息进行参数化，以数据库的形式存储，从而使该套系统可模拟任意船舶的压载水系统。

参数化的模型数据包括：初始化数据、压载水舱数据、管元数据、节点数据。其中：(1)初始化数据包含船长、船宽、型深等船型信息，以及压载水舱个数、压载泵个数、阀门个数等压载系统信息；(2)压载水舱数据包含压载水舱的编号、名称和舱容信息；(3)管元数据包含管元号、管元类型(将管路单元分类为含泵管元、含阀管元和光管)、管元两端的节点号、含阀管元的阀门型式等；(4)节点数据包含节点号、节点类型(将节点分类为吸水节点、泄放节点和中间节点)、节点坐标、与之相连的单元号等。

用户通过软件的新建工程向导，将上述各项数据信息导入后，仿真系统可自动生成船舶压载水管网模型并完成初始化。建好的模型以数据库格式保存，并可输出为Excel文件，以方便模型的检查与更新。用户可选择手动模式或自动模式进行压载水调节。在手动模式下，用户通过开闭压载泵和阀门，可实时观察管路流通情况和压载舱的液位变化情况。在自动模式下，用户设置各压载舱初始液位信息及目标浮态，系统可自动生成调载方案。

3 调载优化算法

压载水调载方案优化有多种方法。不同的船型配载问题，采用的解决方法也有所不同。模拟进化算法、模糊控制法、惩罚函数法、内点法、乘子法等可用于驳船配载[8-10]，问题模型通常为单目标函数。而对于起重船，其作业过程中的配载问题大多是纵倾和横倾角度的多目标函数。解决多目标优化问题的方法有向量评估遗传算法、非劣分层遗传算法、多目标粒子群优化算法、微遗传算法等。所开发的仿真系统主要采用NSGA-Ⅱ算法和反向传播(Back Propagation,BP)神经网络方法来实现船舶调载方案的优化。

3.1 基于NSGA-Ⅱ算法的自动调载

NSGA-Ⅱ算法是一种带精英策略的非支配排序遗传算法。该方法在解决多目标优化问题时，采用的不是传统遗传算法的惩罚法、加权法或混合法，而是采用一种非支配排序的机制，并且通过引入精英保留策略和拥挤距离，简化参数选取，提高算法性能，使结果逼近Pareto最优值。

在船舶自动调载问题中，通常有多个目标函数，如吃水、纵倾角度、横倾角度等。自变量为压载舱的变化水量，因此自变量的个数取决于压载水舱的数量。对于大型船舶，压载水舱数量众多，则算法应用中的染色体的长度较长，解空间较大，容易陷入局部最优解，出现早熟问题。为解决该问题，使用启发式加权交叉算子使交叉算子系数与进化代数及个体在种群中的等级相关，确保搜索方向朝着真正的Pareto最优曲面进行。此种算法的合理性与有效性在文献[7]中已有论述。算法流程如图2所示。

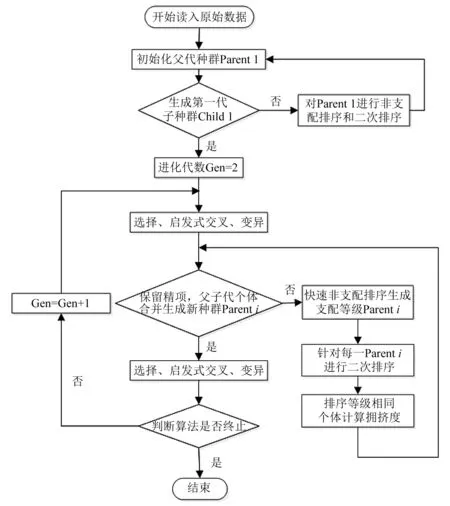
图2 NSGA-Ⅱ算法优化流程

压载水仿真系统中，NSGA-Ⅱ算法的实现如下：

(1) 遗传编码。船舶压载舱的舱容从几十立方米至几千立方米不等，既不利于编码又占用计算资源。在所开发的仿真系统中，调载算法将压载舱调载水量占舱容的百分比设为自变量。设压载舱i的初始水量百分比为pi，则自变量取值最大为1-pi，最小为-pi。

如何实现这一突破，实现华裔青少年族群意识的恢复、华族文化的认同、华语能力的掌握及华语水平的提高，数年来一直是老一辈华族、中国政府及华文教育者所思考的问题。中国国务院侨办“寻根之旅”活动的推出，为我们提供了一条解决这一难题的极好途径。俗语说：读万卷书，行万里路，百闻不如一见。“中国寻根之旅”就是培养文化认同最直接、最有效的途径之一。因为，开展此类活动，可以让华裔青少年身临祖籍国，通过耳闻目睹，解决祖籍认同问题，恢复华族自信心，提高民族自豪感，进而自觉地担当起华族优秀文化学习和传承的重任，做一个名副其实的华人。

(2) 适应度函数。根据用户输入的调载目标构造适应度函数。若调载目标为纵横倾角度时，将同时满足条件的个体按调载总量大小排序，选出调载量最小的解作为推荐的调载方案。若调载目标为平均吃水和倾角时，将同时满足条件的个体按调载舱个数多少排序，选出调载舱数最少的解作为推荐的调载方案。

(3) 非支配排序。引入精英策略，对满足自变量范围的种群进行非支配排序，从而将种群划分为多个非支配层。

(4) 拥挤距离。为了防止种群在局部聚集，保证种群的多样性，引入拥挤距离。将某个体与同一层相邻个体组成的最小矩形的两邻边之和定义为该点的拥挤距离，拥挤距离大的个体被保留。

(5) 遗传算子。包括选择、交叉和变异算子。首先，随机选取种群交配库中个体的一半作为父代，为保证种群多样性生成更多的新个体，将该种群与子代种群合并生成新种群，再进行非支配排序生成支配等级，二次排序后，针对每一等级的个体计算拥挤度并从中选出优解作为下一循环的父代，继续循环种群直至找到满意解为止。

(6) 调载参数设置。通过调载参数设置界面，用户可设定调载目标、压载舱初始水量信息、约束条件、种群规模、遗传代数、约束条件松弛因子、交叉概率、变异概率等。通过更换合理的参数，获得较优的调载方案。

3.2 基于BP神经网络的调载方案搜索

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络。这种方法无需事先确定输入输出之间映射的数学方程，仅通过自身的训练，学习某种规则，就可在给定输入值时得到最接近期望输出值的结果。

所开发的仿真系统设计调载方案数据库，用户可对每次调载作业的最终方案进行保存。系统自动统计该方案的初始条件、调载总水量、空舱数、满舱数、纵倾角、横倾角等，生成数据表记录。这些不断更新的记录将作为BP神经网络学习的训练集和测试集。BP神经网络算法通过MATLAB编写的输入层、隐含层和输出层等3层结构实现。当新的调载条件输入至训练好的神经网络时，输出即为建议的调载方案。

由于BP神经网络学习的效果在很大程度上依赖于训练样本的规模和质量，因此这种搜索的方法同样建立在调载方案数量和质量的基础上。如果数据库中保存的方案数量过少，BP算法就没有足够的训练集；如果方案的初始条件过于相似，不能提供多样化的训练样本，就会在出现新的初始条件时，无法通过学习获得合适的调载方案。在调载方案数据库中的记录数达到一定数量并呈现多样化时，使用BP神经网络搜索可以更快速地获得较优的调载方案。

4 某船压载水系统仿真实例

使用所开发的仿真系统分别对某半潜运输船和某起重船的压载水系统进行仿真，验证其通用性和可靠性。

4.1 某半潜运输船的压载水系统仿真

该船压载水系统有55个压载水舱，4台两两并联的压载水泵，2个高位海水门吸水口，2个低位海水门吸水口，2个排舷外泄放口。对压载水管网进行有限元分解，可得到141个管元、136个节点。通过参数化建模向导，该船压载水系统的仿真模型如图3所示，分为艏部压载系统和艉部压载系统，通过控制管路阀门和压载泵的开关状态，可实现任意压载水舱的注水和排水状况模拟，也可实现在海水门和排舷外阀门全部关闭时，船内压载水舱之间的调拨模拟。监控组件实时显示压载水舱的水量、液位高度和压载水量占舱容的百分比。

图3 某半潜运输船压载水系统仿真界面

图3中，船舶的初始工况为空载，吃水位于设计水线9.30 m处，纵倾角度为0°。此时，船上的压载水舱装载情况如表1所示。

表1 某半潜运输船初始工况压载舱装载量 %

该船拟运输一自重为2 000 t的自升式钻井平台，在平台运至半潜运输船之前，需将半潜船压载至甲板完全浸没。该压载过程中某中间工况的目标吃水为11.50 m，适当艏倾。使用所开发的仿真系统的自动调载功能，对该工况进行自动调载计算。计算参数设置：种群规模50，遗传代数20，约束条件的松弛因子10-4，交叉概率0.9，变异概率0.1。计算得到的推荐压载水调节方案如表2所示。

表2 某半潜运输船压载水调节方案 %

该方案调节压载水舱24个，压载水量增加18 898 t。调载后，船舶的平均吃水为11.65 m，艏倾1.9°，达到目标要求。

4.2 某起重船的压载水系统仿真

该船压载水系统有30个压载水舱，4台压载水泵，4个海水门吸水口，4个排舷外泄放口。使用与第4.1节中同样的建模方法，对压载水管网进行有限元分解，可得到108个管元、96个节点。通过参数化建模向导，该船压载水系统的仿真模型如图4所示，1个界面即可将系统完整表达。

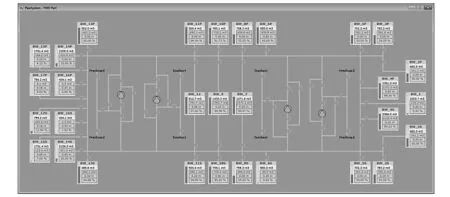
图4 某起重船压载水系统仿真界面

该起重船拟在右舷起重2 700 t的货物，在其预压载工况时，吃水为9.44 m处，艏倾-0.38 m。此时，船上的压载水舱装载情况如表3所示。

表3 某起重船预压载工况压载舱装载量 %

货物完全起升后，要求船舶基本无横倾。经过自动调载计算，给出推荐的压载水调节方案如表4所示。

表4 某起重船压载水调节方案 %

该方案调节压载水舱8个，均为舱内调载。调载后船舶的横倾角度为0.1°，达到目标要求。

5 结 论

(1) 通过在不同船舶上的实例应用证明，基于管网有限元法所建立的船舶压载系统参数化建模方法是有效的，可使所开发的仿真系统具有较强的通用性，解决同类仿真软件仅能针对某些特定船舶的局限性问题。

(2) 所开发的仿真系统可按照设定的调载目标自动生成调载方案，通过对调载后的船舶浮态进行计算，验证所生成的调载方案能够满足要求。这种自动调载功能可辅助操作人员决策，减小因操作人员经验不足带来的作业风险。

(3) 由于不同船舶压载系统的特点各异，一种优化算法并不一定能得到全局最优的调载方案。因此下一步的仿真系统升级中可考虑引入多种优化算法，通过对结果进行比较，为操作人员提供更优的方案。