基于MATLAB的汽车塑料内饰件打磨路径规划仿真

刘鸿飞， 徐斯诺， 连 山

(北京科技大学 机械工程学院， 北京 100083)

在近20年的发展过程中，我国工业机器人的应用能力及研究状况有了很大的改善，已经处于世界领先水平[1-5]。卢宏亮[6]利用UR5机器人搭建了一套焊缝打磨机器人系统；王敏[7]对轮毂打磨机器人的关键技术进行了研究；崔国华等[8]设计了一种新型便携式管口打磨机器人；温宇翔[9]针对汽车冲压件设计了一套基于多传感器的机器人打磨系统；张一然等[10]以碳纤维复合材料为研究对象,开展基于工业机器人工作站的打磨关键技术及工艺研究。越来越多的工程项目开始选用工业机器人作为替代人工作业的最优方案。

吉林省长春市某注塑厂为某合资品牌生产的2020款新车型车门装饰面板，需进行打磨作业。为保护工人身心健康，提高打磨效率，提出采用工业机器人打磨工作站方案代替人工打磨作业。由于待打磨零件形状复杂，课题组进行了打磨路径规划，并利用MATLAB仿真以检验工作效率。

1 打磨任务综述

待打磨零件的实物如图1所示。零件材料为ABS 塑料。由于注塑工艺原理上的原因，在成品的合模线附近会产生毛边和尖刺，不仅会影响零件后续的喷漆和装配，也会影响产品的美观性和安全性，因此需要对合模线附近的毛边和尖刺进行打磨处理。

图1 待打磨注塑零件实物图Figure 1 Physical picture of injection parts to be polished

注塑厂可用的打磨机器人为广东某智能装备股份有限公司生产的BRTIRSE 1506A型6自由度工业机器人，如图2所示。

图2 BRTIRSE 1506A工业机器人Figure 2 BRTIRSE 1506A industrial robot

在机器人末端安装气动柔性主轴，如图3(a)所示，夹持打磨头进行打磨作业。为选择合适型号的打磨头，准备了25套待打磨零件和10种不同类型的打磨头，如图3(b)所示，进行对比试验。对比后，打磨效果最优的为10#单槽型硬质合金打磨头，故选其作为工作打磨头。打磨效果如图3(c)所示。

图3 气动主轴、打磨头试样及10#打磨头打磨效果Figure 3 Pneumatic spindle, grinding head sample and 10# grinding head grinding effect

2 运动规划策略的选择

工业机器人的运动规划策略主要分为2类：关节空间运动规划和笛卡尔空间运动规划[11]。笛卡尔空间运动规划的关注重点在末端的运动轨迹，规划生成的是机器人末端的位姿参数。从数学角度描述，实质上就是建立一个机器人末端位姿关于时间的函数[12]。

课题组将打磨路径设计为一次走刀打磨一对镜像零件，如图4所示。

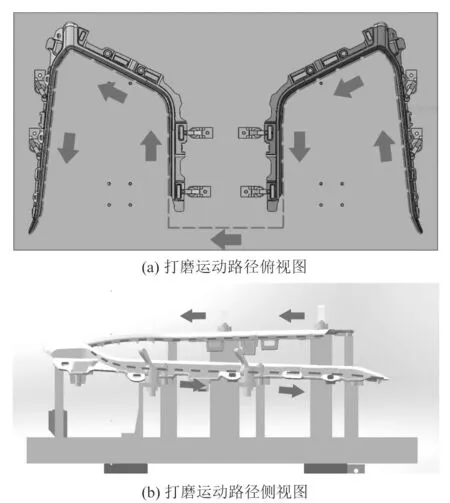
图4 打磨运动路径示意图Figure 4 Schematic diagram of polishing movement path

打磨头走过的路径中，曲率半径较小的曲线很多，且打磨头中心点在水平方向和竖直方向均要运动，路径较为复杂，详见图4中虚线及箭头。

由于期望机器人的末端能够严格按照规定好的路线进行运动，选用笛卡尔空间运动规划可以实时获取机器人末端的位姿情况，便于进行避障和调整运动路径，因此运动规划策略选择笛卡尔空间运动规划策略。

3 运动路径插补

机器人的运动路径可近似分割成若干段直线路径和曲线路径。在各段直线路径和曲线路径的起点和终点之间，插入中间点序列，实现沿着轨迹的平稳运动，这就是运动路径插补的内容[13]。

因此课题组利用MATLAB 软件中的Robotic Toolbox工具箱，对直线路径部分和曲线路径部分分别采用不同的插补算法，实现打磨路径的插补。

3.1 空间直线路径插补算法

设已知空间直线段的始末坐标为Ps(xs,ys,zs)，Pe(xe,ye,ze)。设v为机器人末端沿空间直线的运动速度，单位m/s。Ts为插补周期，单位s。

因此，空间直线长度L(单位m)为

末端走过这段空间之间所需的移动时间T(单位s)为

空间直线插补所需的步数N为(ent表示取整运算，Ts为插补周期)：

在笛卡尔坐标系中，空间直线的终点坐标在x，y，z各轴上相对于起点坐标的增量Δx，Δy，Δz分别为：

Δx=xe-xs;

Δy=ye-ys;

Δz=ze-zs。

各插补点的坐标值为：

xi+1=xi+λΔx;

yi+1=yi+λΔy;

zi+1=zi+λΔz。

式中：xi为第i个插补点的x轴坐标值;xi+1为第i+1个插补点的x轴坐标值，以此类推。

其中：

式中：i表示插补点的序号，N表示空间直线插补所需的步数。

当λ=0时，对应空间直线的起点；当λ=1时，对应空间直线的终点。

3.2 空间圆弧路径插补算法

由数学基础知识可知：不共线的3点可确定一条圆弧。设一段圆弧的始末坐标分别为Ps(xs,ys,zs)，Pe(xe,ye,ze)，圆弧上任意一点坐标为Pd(xd,yd,zd)，圆心为Pc(xc,yc,zc)，圆弧半径为R，单位m。

1) 圆心Pc(xc,yc,zc)与圆弧半径R的确定

Ps(xs,ys,zs)，Pd(xd,yd,zd)，Pe(xe,ye,ze)为不共线的3点，构成的圆弧确定1个平面Q，可表示为：

经行列式运算展开后，得

[(ys-ye)(zd-ze)-(yd-ye)(zs-ze)](x-xe)+[(xd-xe)(zs-ze)-(xs-xe)(zd-ze)](y-ye)+[(xs-xe)(yd-ye)-(xd-xe)(ys-ye)](z-ze)=0。

设有一平面A，过PsPd连线中点且与PsPd连线垂直，其方程为

设有一平面B，过PdPe连线中点且与PdPe连线垂直，其方程为

将3个平面Q，A，B的方程联立，利用消元法可求出圆心Pc(xc,yc,zc)的坐标。

圆弧半径R的求解：

2) 建立Qr-lmn坐标系

设圆心Pc(xc,yc,zc)为笛卡尔坐标系原点Qr，取PcPs方向为m轴方向。其m轴的单位方向向量为

设PcPs和PcPe所构成平面的法线方向为n轴，正方向满足右手定则，即n轴为PcPs和PcPe的向量积方向。n轴的单位方向向量为

按照右手定则的判定，l轴在m轴与n轴的向量积方向，其单位方向向量为

l=m×n。

3) 坐标变换矩阵TR

由齐次变换矩阵的定义可写出变换矩阵TR：

可得：

4) 坐标值的变换

mc=lc=nc=ns=nd=ne=0,ms=R。

上述为空间曲线路径插补算法。

3.3 运动路径的仿真实现

笛卡尔空间规划函数“ctraj”所需的自变量为始末点的笛卡尔坐标值以及速度值或加速度值[14-15]。但传统的笛卡尔空间规划函数“ctraj”仅可以对空间直线路径进行插补运算，无法进行空间曲线路径插补。

为实现空间曲线路径插补任务，笔者对传统的笛卡尔空间规划函数进行改进。编写了实现圆心Pc(xc,yc,zc)坐标计算的CalCircleCenter算法，实现圆弧半径R计算的Distance算法，以及对圆弧圆心角度计算的CalCentralAngle算法。采用无限逼近的总体思路，即在圆弧上设置若干个关键插补点，套用传统的笛卡尔空间规划函数，在插补点间插补若干极短直线来无限拟合出目标圆弧曲线。

空间圆弧插补函数CirInterpolation通过前序算法得到的空间圆弧的起点、中间点和终点，以及人为设置的插补点数目，计算出插补点的位置。

图5 空间圆弧插补函数CirInterpolation部分代码Figure 5 Part code of spatial arc interpolation function CirInterpolation

由于待打磨零件为左右对称的镜像零件(见图4)，考虑到计算机的计算能力，笔者仅对单侧零件的打磨运动路径进行仿真实验。将打磨路径插补任务分割为5段直线插补和3段圆弧插补。

仿真演示中设置了机器人的实时动态显示的环节，可以方便地看出机器人的位姿与末端曲线间的关系，如图6所示。

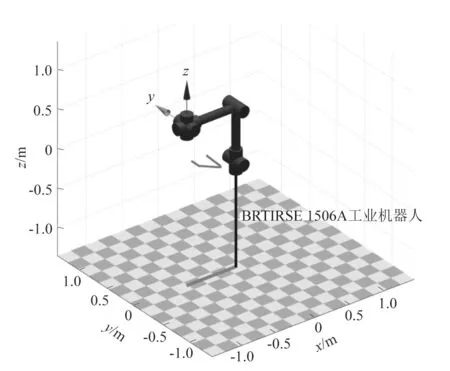
图6 BRTIRSE 1506A工业机器人位姿与末端路径同步显示Figure 6 Synchronized display of BRTIRSE 1506A industrial robot pose and end path

在运动路径仿真实验中，调用“探查器”对打磨路径运动进行计时测试：单侧零件的打磨时间为79 s，探查结果见图7。前期现场调研时，对注塑厂的打磨工人工作效率情况进行过统计，熟练的打磨工人打磨单侧零件的耗时约为120 s。经计算，工业机器人打磨相比人工打磨效率提升约34%。

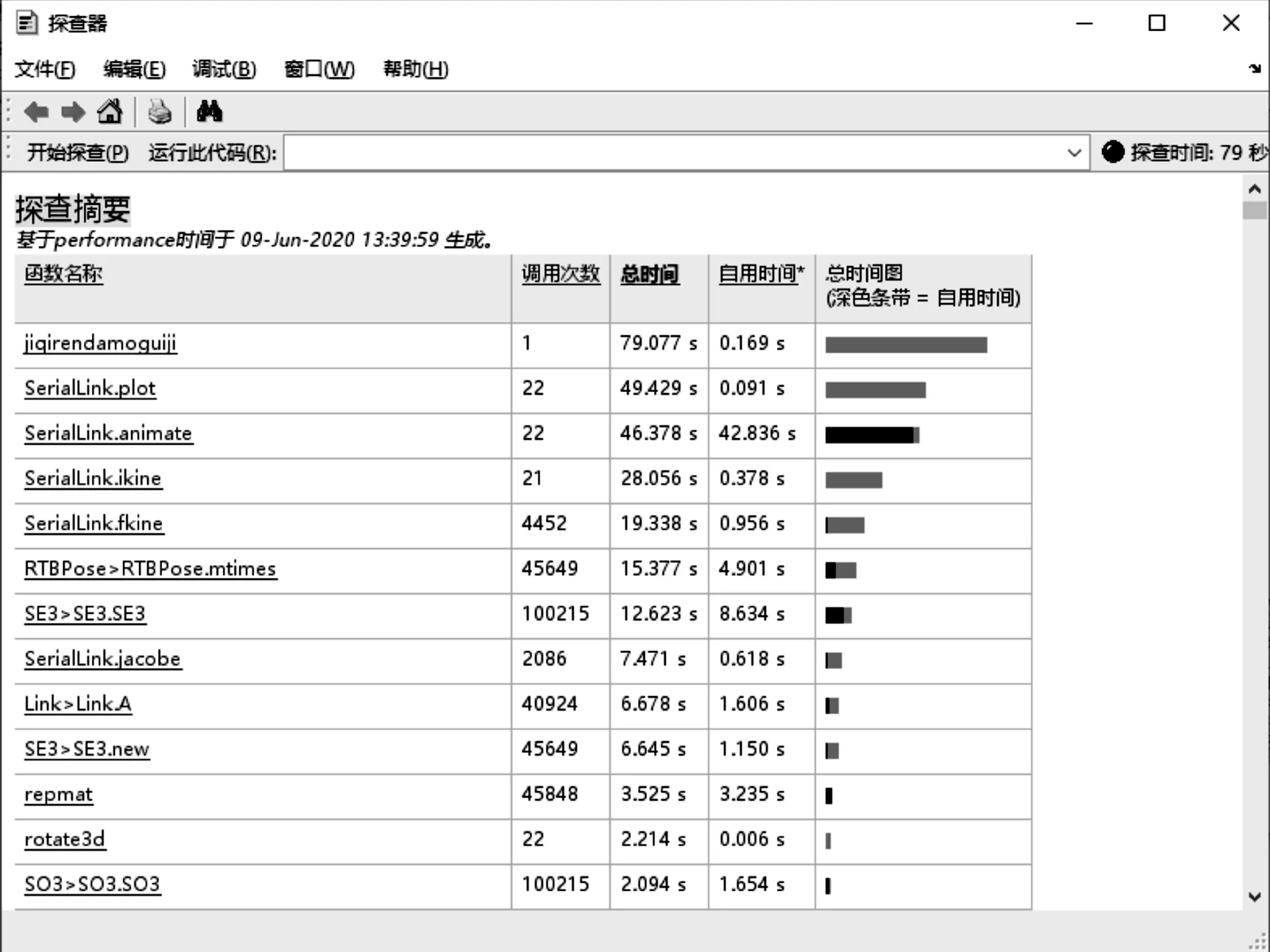
图7 MATLAB探查器结果Figure 7 MATLAB profiler results

6自由度工业机器人BRTIRSE 1506A完成单侧零件打磨的打磨头末端运动路径如图8所示。其中虚线表示与工件接触后的打磨工作路径，实线表示从打磨头进入和离开工作点的运动路径。

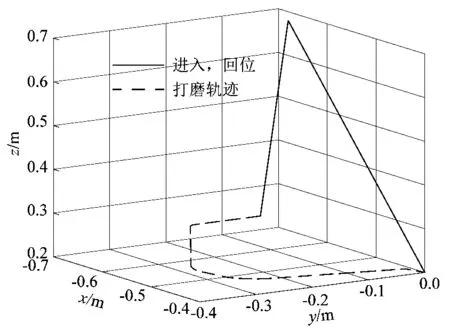
图8 单侧工件打磨运动路径的实现Figure 8 Realization of polishing motion path of single side workpiece

4 结语

目前，工业机器人应用于打磨抛光领域的成功案例数量可观，但相当部分都是针对焊缝打磨或金属表面处理，针对塑料零件打磨的方向还有待于开发和补充。课题组依托于注塑厂实际工程项目，针对人工打磨塑料件危害身心健康且效率低下的缺点，提出了引入工业机器人打磨工作站替代人工作业的方案，并成功设计打磨工作站的关键内容。工业机器人替代人工打磨实现了保护工人身心健康的目的；通过MATLAB平台仿真实验，表明工业机器人打磨相较人工打磨效率提升34%，解决了工厂的重大难题，具有重要的实用意义。在提高了打磨效率的基础之上，为进一步提高打磨工作站的工作质量，还应继续对机器人打磨精度的提高展开研究，对于本课题同样具有重要的意义。