新型大行程高承载力的柔性铰链设计

赵传森， 许 勇， 张强强， 王 艳， 董 飞

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

随着柔性机构的飞速发展，具有尺寸紧凑、轻量化、无摩擦、无润滑和无磨损等优点的柔性铰链和柔性机构已经在汽车工业、电子工业、微操作机器人及精密光学仪器等领域得到广泛应用[1-5]。

对于柔性铰链的研究已经有了大量的文献参考[6-7]。JACOBSEN等[8]提出了平板折展扭转柔性铰链(LET)，推导了铰链的扭转等效刚度和拉压等效刚度，并进行了有限元验证，表明LET铰链适用于需要大角度旋转但离轴刚度不高的应用范畴。李宗轩等[9]提出了一种Cartwheel 型双轴柔性铰链，该铰链结构是由带圆角的短直梁复合而成，利用有限元分析的方法对其刚度和应力性能指标进行了分析验证，确定了其几何尺寸。陈贵敏等[10]提出了一类深切口椭圆柔性铰链，运用材料力学理论推导了转角、精度和最大应力解析公式，运用Ansys有限元仿真软件验证了公式的正确性。宗光华等[11]发明了一种双曲杆型空心柔性铰链，该铰链中间是空心设计，用簧片式代替传统的切口型柔性铰链，提高了转动范围并降低了内应力，适用于大行程的工程应用。文献[12-13]发明了一种交叉簧片转动型柔性铰链，通过多簧片在空间交叉但并不在交叉点处固定的设计，使得铰链的变形更大，精度较高。GOLDFARB等[14]提出了一种具有独特旋转弯曲的裂桶型柔性铰链，通过提供更好的多轴旋转特性，对比传统的薄梁弯曲铰链，该铰链能够实现更大的运动范围。

这些柔性铰链虽然都有自己的优势表现，但很难同时满足行程、承载能力及失效等性能指标要求，多数柔性铰链存在轴漂大、承载力小、塑性变形及稳定性差等问题。为了解决这些问题，很多学者将研究集中到开发新型柔性铰链中。有鉴于此，课题组也力求从这些角度进行突破，提出了一种新型TLET柔性铰链。该铰链具有行程大，承载能力大，工作环境安全可靠等特点，在现代机构发展阶段中具有潜在的应用前景。

课题组设计了一种具有大行程、高承载力的新型柔性铰链(TLET)。将LET柔性铰链以串并联的方式布置，建立了等效刚度模型。对不同材料的柔性铰链进行了失效分析，通过有限元仿真验证了铰链的可行性。最后将新型TLET柔性铰链和传统LET柔性铰链进行了比较。

1 新型柔性铰链设计

为了使柔性铰链受力时产生较大的位移范围，课题组提出一种新型LET阵列，命名为TLET铰链，如图1所示。传统设计方案，一般只设计为2个分支，但有些特殊需求，需要增加分支的数量。一组耦合的LET分支被改变时，位移和刚度都会发生改变。在本文中，我们选择2个耦合的LET铰链来研究整个柔性铰链的性能。基于LET铰链阵列，所提出的柔性铰链在x轴方向有较大位移，载荷范围较大，同时z轴方向也有较大位移。LET铰链分别由扭杆1、扭杆2和弯杆1、弯杆2组成。利用串并联布置方式的特性，可以增大沿x轴和z轴方向上的位移。

图1 TLET柔性铰链三维模型Figure 1 3D model of TLET flexure hinge

图2为新型柔性铰链的二维几何尺寸图。TLET铰链在水平方向和竖直方向上对称分布，包括厚度t、宽度w、长度l以及扭杆和弯杆的几何参数。扭杆1和扭杆2的长度分别为lT1和lT2，宽度分别为wT1和wT2;弯杆1和弯杆2的长度分别为lB1和lB2，宽度分别为wB1和wB2。表1给出了铰链的主要几何参数的详细说明。

图2 TLET柔性铰链的二维几何尺寸Figure 2 Two-dimensional geometry of a TLET flexure hinge

表1 柔性铰链设计参数的详细说明Table 1 Detailed description of flexure hinge design parameters mm

边界条件如下：沿x轴在A点施加压缩荷载F，产生x轴方向压缩位移和平面外z轴方向的位移。

2 等效刚度模型的建立

为了分析TLET柔性铰链的刚度性能，我们确定了弹簧常数的等效方程。把每个节段都假设为弹簧，同时每个弯杆和扭杆都简化为弯曲和扭转弹簧，如图3所示。TLET铰链的整体刚度可分为弹簧系统Ⅰ、Ⅱ，其中弯杆2连接这2个系统，分别将kT1，kB1和kT2串联再并联，形成一个整体系统，标记为弹簧系统Ⅰ；同理，可得到弹簧系统Ⅱ。

考虑到系统Ⅰ的上部，包括3个串联的kT1，kB1和kT2，其等效刚度为

式中：keq,topⅠ，kT1，kB1和kT2分别表示弹簧系统Ⅰ上部的等效刚度，扭杆1的刚度，弯杆1和扭杆2的刚度。

系统Ⅰ的下部与上部相同，因此弹簧系统Ⅰ的总等效刚度为

式中KeqⅠ表示弹簧系统Ⅰ的总等效刚度。

由于柔性铰链对称布置，弹簧系统Ⅱ的总等效刚度等于弹簧系统Ⅰ的总等效刚度，即

式中KeqⅡ表示弹簧系统Ⅱ的总等效刚度。

如图3所示，所有弹簧都是串并联的。基于此假设，TLET型柔性铰链的总等效弹簧常数Keq，TLET为

其中弯杆1和弯杆2的刚度计算公式为：

式中E是弹性模量。

扭杆1和扭杆2的刚度计算公式为：

式中：G是刚性模量，ν是泊松比。

沿x轴输入载荷与TLET柔性铰链输出位移之间的关系为

式中：F为载荷，δ为柔性铰链沿x轴的位移。

图3 TLET柔性铰链等效弹簧模型Figure 3 Equivalent spring model of TLET flexure hinge

3 失效分析

在柔性铰链工作过程中，会出现蠕变、屈曲、塑性变形和疲劳断裂等失效形式，其中塑性变形破坏和屈曲现象是柔性铰链最需要解决的两种失效形式。提出的柔性铰链需在材料的弹性极限范围内安全工作，因此，要分析解决这些失效形式，才能保证铰链安全工作。

3.1 塑性变形破坏

柔性铰链只有在合理的弹性变形范围内才能满足实际应用，失效分析的目的是保证铰链能够正常安全工作。因此，在本节中考虑了铰链的应力极限和变形范围。众所周知，如果铰链的总应力高于材料的屈服强度，则铰链失效形式为塑性变形破坏。因此，在大位移、大载荷范围内选择合适的材料是考虑的关键问题。

为了对这一问题进行深入分析，笔者比较了结构钢、不锈钢和超硬铝3种材料制成的柔性铰链的性能。采用有限元分析的方法，先建立了三维模型，然后利用Ansys workbench软件进行了有限元分析，对网格进行划分；分析采用了非线性条件，以保证收敛结果。表2给出了仿真中每种材料的力学性能，每种材料的失效分析旨在确定铰链的最大载荷、最大应力极限和最大位移。在所有情况下，都考虑了等效应力。沿x轴设置了边界条件和荷载F，如图4所示。

图4 TLET柔性铰链的网格模型Figure 4 Grid model of TLET flexure hinge

如表2所示，当柔性铰链材料为结构钢时，可沿x轴承受24 N的最大载荷，在该载荷作用下，柔性铰链沿着x轴的最大位移为4.66 mm，此时最大应力为243.68 MPa，比结构钢的屈服强度(250 MPa)小。当采用不锈钢材料时，柔性铰链可承受20 N的最大载荷，沿x轴方向的最大位移为4.03 mm，最大应力为203.07 MPa，比不锈钢的屈服强度(206 MPa)小。

结果以“平均值±标准差”表示，数据处理与分析采用SPSS 16.0统计软件进行方差分析和差异显著性比较，以P＜0.05作为差异显著性判断标准。

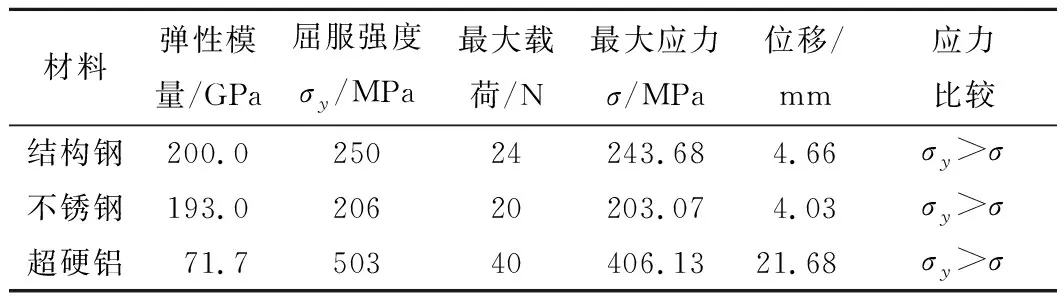
表2 不同材料TLET柔性铰链的失效分析

结果表明：上述材料保证了柔性铰链可靠、安全的工作条件。尽管柔性铰链允许大的工作行程，但只能承受24 N的最大载荷。笔者考虑了承载力大和工作行程大的特性，决定采用超硬铝作为柔性铰链的替代材料。

用超硬铝制造的柔性铰链在自由端施加40 N的载荷时，沿x轴方向可产生21.68 mm的位移，由此产生的最大应力为406.13 MPa。远比超硬铝的屈服强度(503 MPa)小。说明了柔性铰链可以安全工作，不会发生塑性变形失效。当载荷增加到50 N时，可沿x轴方向移动27.1 mm，但产生的最大应力为507.67 MPa，大于材料的屈服强度。说明在50 N及以上载荷下，柔性铰链无法保证可靠性。因此超硬铝制成的柔性铰链的最大载荷应取40 N。

3.2 屈曲性能分析

本节分析前2种屈曲模态。第1种模态：在载荷F的作用下，柔性铰链沿x轴方向被压缩而产生位移。第2种模态：在载荷F的作用下，柔性铰链沿着z轴方向发生平面外的位移。对这2种模态进行分析，以得到其倍增载荷因子。在所有的屈曲模态中，前2个倍增载荷因子最小。因此，笔者考虑前2个屈曲性能模态来确定前2个倍增荷载因子。对于悬臂梁，可以确定临界屈曲荷载Pc[15]为

式中：E是弹性模量，I是面积的二阶矩，l是铰链长度。

此外，临界屈曲荷载方程可简化为

Pc=λ×PI。

式中：λ为倍增载荷因子，PI是初始屈曲载荷。

通过重复使用表2中每种材料的最大载荷值，TLET铰链可能会受到屈曲性能的影响。利用有限元分析，对不同材料的TLET铰链的倍增载荷因子λ进行了分析。表3结果表明，采用超硬铝材料制成的柔性铰链的倍增载荷因子低于结构钢和不锈钢，说明采用超硬铝材料稳定性较好。

表3 不同材料屈曲性能的结果

4 TLET柔性铰链与LET柔性铰链的性能比较

为了分析TLET铰链的大行程、高承载力的突出性能，将其与传统的LET铰链进行比较。图5为传统LET铰链的二维模型，长度为60 mm、宽度为150 mm，尺寸参数和TLET铰链相等。

图5 传统LET柔性铰链的二维模型Figure 5 Two-dimensional model of a traditional LET flexure hinge

图6表明TLET柔性铰链的位移比传统铰链的位移大，并且是传统LET铰链位移的1.8倍，说明所设计的柔性铰链行程性能优于传统柔性铰链。如果减小传统柔性铰链的厚度其输出位移将会得到改善，但由于新型柔性铰链是由2个柔性铰链组成的阵列，因此其输出位移相对更好。

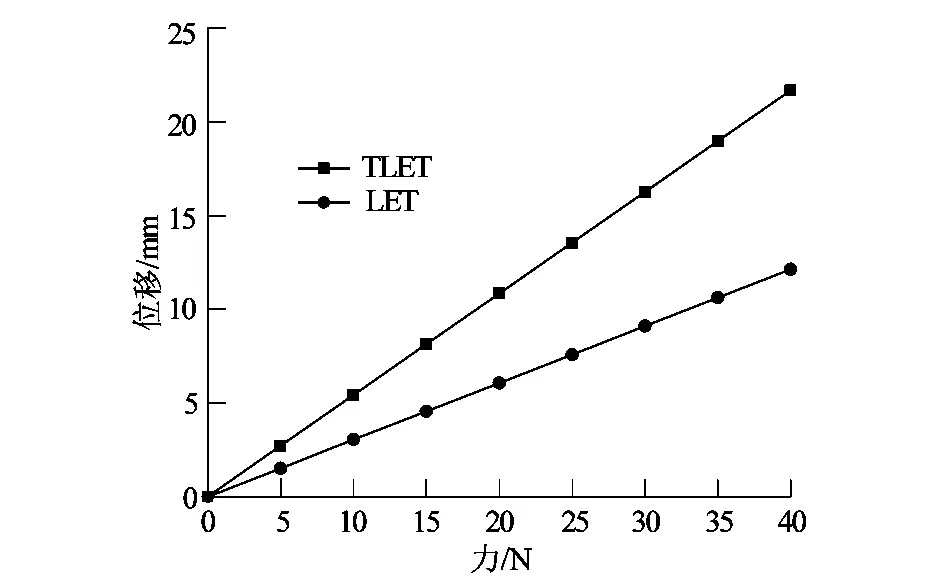
图6 LET铰链和TLET铰链的力-位移比较Figure 6 Force-displacement comparison of LET and TLET hinges

考虑到屈曲变形现象，我们分析了二者倍增载荷因子的大小。由图7可以得到新型铰链的倍增载荷因子比传统铰链低，说明TLET铰链的稳定性比传统铰链好。

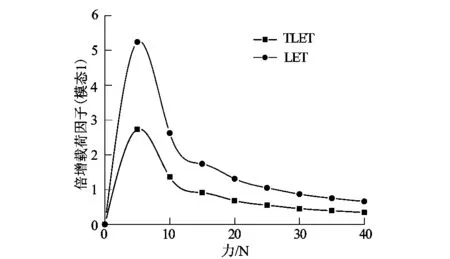
图7 LET铰链和TLET铰链的力-倍增载荷因子比较Figure 7 Comparison of force-multiplier load factors for LET and TLET hinges

当TLET铰链沿x轴方向承受压缩载荷时，TLET不仅沿x轴方向移动，也沿z轴方向移动。这意味着x轴方向上的位移点对应于z轴上的位移点。因此，可以得出TLET铰链沿x轴的输入位移和沿z轴的输出位移之间的关系，如图8所示。

结果表明：TLET铰链沿x轴的输出位移范围为2.41～21.68 mm，沿着z轴的输出位移范围为5.00～25.12 mm。综上所述，TLET型柔性铰链沿x轴可实现21.68 mm的大工作行程，沿z轴可实现25.12 mm的大工作行程，TLET铰链的性能远大于传统的LET铰链。对于要求变形量大、承载能力强的工作场合，建议采用TLET型柔性铰链。

图8 TLET柔性铰链沿x轴和沿z轴位移的关系Figure 8 Diagram of displacement of TLET flexure hinge along x axis and z axis

5 结语

1) 课题组提出了一种新型柔性铰链，通过将2个LET柔性铰链以串并联的方式重新配置，使其能够实现大行程，高承载能力和安全工作状态而不发生失效。

2) 课题组推导了TLET柔性铰链等效刚度的解析模型，验证了不同材料下铰链的塑性变形，最大应力和屈曲失稳行为。

3) 由于TLET铰链仅在特定材料的弹性极限下工作，因此课题组对其失效形式进行了分析。课题组对结构钢、不锈钢和超硬铝等几种常用材料进行了研究和比较，分析了每种情况下的塑性变形破坏和屈曲变形，选用了超硬铝作为铰链的材料。

4) 课题组运用有限元法进行分析仿真，结果表明，当载荷作用于TLET型铰链的自由端时，沿着x轴的最大输入位移为21.68 mm，沿着z轴可获得超过25.12 mm的位移。并且能够承受高达40 N的载荷而不发生失效。与传统LET铰链相比，该铰链的位移是传统铰链的1.8倍。因此文中所设计的铰链可用于工作行程大，负载能力大的机械装备中。