单自由度弹跳机构的跳跃稳定性研究

张强强， 许 勇， 赵传森， 董 飞， 王 艳

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

机器人技术与生物特征的结合，极大地促进了弹跳机器人行业的发展。越来越多的人热衷于仿生机器人，根据动物身体结构、运动特性，设计出更多性能优良的机器人[1]。运动有多种方式，弹跳运动只是其中一种类型的运动，弹跳机器人具有运动能力强、运动面广、避障能力强等特点[2]。

1986年，麻省理工大学Raibert提出了最早的单腿弹跳机构[3-4]，该机构有2个自由度：1个移动自由度和1个转动自由度。美国国家航空和航天局(NASA)发明了仿青蛙的弹跳机构，最大跳跃高度可达1.8 m[5]。2000年，美国明尼苏达大学研制出了一种弹跳机器人,由安在机器人腿内的弹簧机构给机器人提供跳跃动力，属于单腿跳动,它可以跳过小的障碍物，也可以爬楼梯[6]8。2012年，瑞士Leavitt的设计了一种仿蚱蜢弹跳机器人[7]，它的起跳角和起跳力可以变化，跳跃性能优良。东京工业大学的Tsukagoshi等研制了气缸式高空跳伞机器人[8]，通过研究弹跳高度与筒体受压面积的关系，对弹跳机器人本身结构和质量进行了优化设计。

2006年，哈尔滨工业大学的余杭杞研制的4足弹跳机器人，有2套样机模型，但是在能量的利用方面不足，没有自主调节起跳角的功能[9]。2007年，陈勇等研究了仿蝗虫弹跳机器人的运动学参数及受力变化，优化机构的结构参数[10]；2011年，哈尔滨工程大学陈东良等通过对蝗虫跳跃机理及蝗虫腿部特性的研究[11]，设计了弹跳腿机构,分析了该模型的机构学和力学特性。2012年，卢松明等设计了一种具花瓣型结构的机器人仿生脚掌结构，分析了花瓣数目与脚掌抓地性能之间的关系[12]；2015年，陈殿生等对仿蝗虫机构落地过程中的能量分配进行了研究，得到地面对机构弹跳腿的支撑力与弹簧刚度系数之间的函数[13]；2016年，长春理工大学徐成宇等[14]以基圆半径最小作为优化目标，设计了仿蝗虫弹跳机器人后腿机构尺寸，减小了动力凸轮体积。2016年，陈科位等[15]证明了蝗虫的翅膀对其空中姿态具有调节作用；2018年，王寰等[16]设计了的仿蝗虫机器人可实现连续跳跃。

课题组以蝗虫腿部机理为基础，以单自由度的Stephenson Ⅱ型平面6杆机构为研究对象，针对弹跳机构的稳定性做了分析与验证。采用闭环矢量方程对机构进行了运动学分析，利用多目标优化算法求解各个杆长；对6杆弹跳机构的起跳阶段做了运动学稳定性分析，确定了弹跳机构的起跳角度的计算方法；用惯性矩与MATLAB函数求解对机构的动态稳定性做了研究，使机构起跳更加稳定。最后还做了实例验证，证明本机构具有好的稳定性。

1 弹跳腿机构位置模型建立

蝗虫依靠腿部带动躯体，而腿部则主要由跗足、胫骨与股骨构成，相邻2部分由关节连接，如图1所示。当发达的后足在瞬间快速向后摆动，使得原本贴近胫节的腿节骤然伸直，此时跗足下的支撑平面会对蝗虫产生巨大反作用力，借此蝗虫身体便可腾空跃起完成跳跃运动。

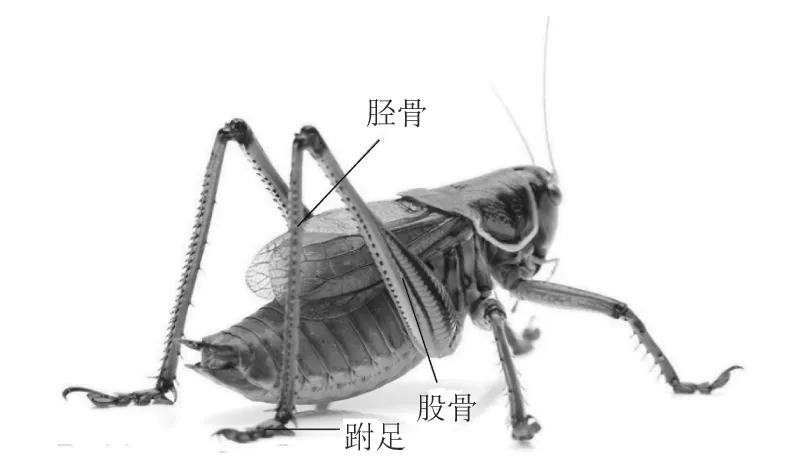
图1 蝗虫身体结构Figure 1 Body structure of locust

通过对蝗虫腿部结构的认知，课题组提出了一种单自由度6杆弹跳腿机构，如图2所示。其中A，B，C，D，E，F，G和H为铰链中心，H点为机构与地面接触点。杆AB连接的是蝗虫的躯干，记为构件1；B点处安装弹性串联驱动器，三角形BCD是6杆腿机构的大腿,记为构件2；连杆CG、连杆AF、连杆DE依次是弹跳腿机构的辅助构件，分别记为构件3、构件4和构件5；四边形EFGH是弹跳腿机构的小腿，记为构件6。

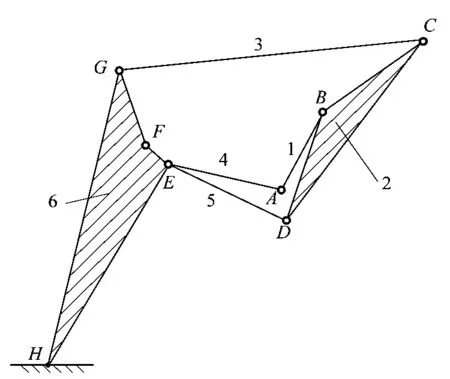
图2 6杆弹跳腿机构示意Figure 2 Schematic diagram of six bar spring leg mechanism

2 机构的静态运动学分析

将6杆弹跳腿机构放置在直角坐标系O-XY中，如图3所示。li(i=1，2，…，6)是6杆弹跳机构的每个杆的长度，lhj(j=1，2，3，4)是弹跳腿机构的小腿EFGH的边长。

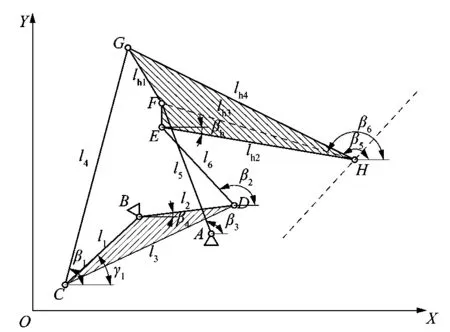
图3 6杆弹跳腿矢量分析Figure 3 Vector analysis diagram of six leg bouncing leg

等效于蝗虫的胫骨，βi(i=1，2，…，4)是弹跳机构的各个连杆和X轴正方向之间的夹角，βh是EH与X轴正方向的夹角，γ1是杆BC与X轴正方向的夹角。

首先对6杆弹跳腿机构进行运动学分析，建立如下的闭环矢量方程。

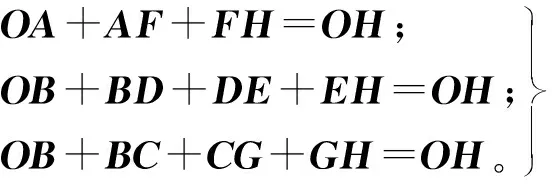
(1)

式(1)中的每个表达式表示1个闭环，3个闭环方程确定6杆机构的所有参数。每个向量方程都可以投影到X和Y轴上，通过各个杆长和每个点坐标以及之间的位置关系，将式(1)转化为标量方程。

(2)

为了方便方程的表述，定义如下中间变量：

Q11=-2(yH-yA);Q21=-2(xH-xA);Q31=(xH-xA)2+(yH-yA)2;
Q12=2(yH-l2sinβ4-yB);Q22=2(xH-l2cosβ4-xB);
Q32=(xH-l2cosβ4-xB)2-(yH-l2sinβ4-yB)2;
Q13=2(yH-l3sin (βh+γ1)-yB);Q23=2(xH-l3cos (βh+γ1)-xB);
Q33=(xH-l3cos (βh+γ1)-xB)2+(yH-l3sin (βh+γ1)-yB)2。

式中：(xA,yA)，(xB，yB)和(xH，yH)分别是点A、点B和点H的坐标。对式(2)进行函数化，可以写成

(3)

式中：βh，γ1和β4可视为已知值，点A和点B的坐标已知。

式(3)表示未知数为li(i=1，2，…，6)、lhj(j=1，3，4)、βk(k=5，6)，方程的数目超过未知数的数目，所以采用多目标优化方法——NSGA-Ⅱ算法(一种基于Pareto最优解的多目标优化算法)，目标函数可以表示为

(4)

式中λj是权重系数。当目标函数的绝对值最小化，机构的运动稳定性更好。

3 起飞阶段的运动学分析

在起飞过程中，6杆机构弹跳腿的示意图如图4所示。以H为坐标原点建立了H-XHYH坐标系，XH轴的正方向是水平向右，YH轴的正方向是垂直向上。假设图4中Mo为此机构的质心点，在6杆弹跳腿机构中转动副A，E，G角度变化较大，所以在这3个位置安装扭矩弹簧。在起飞过程中，弹跳腿机构绕着触地点H点旋转，此处可以简化为一个形心为点H的旋转副。

图4 6杆弹跳腿质心图Figure 4 Centroid diagram of six leg bouncing leg

确定质心的初始位置后(xMo，yMo)，即在起飞过程中质心的运动轨迹也被确定。起飞方向角Φ，也就是弹跳腿机构的蹬地产生的反作用力和XH轴正方向之间的夹角，经推导得

(5)

式中：m是机器人的质量。(FAx，FAy)和(FBx，FBy)是6杆弹跳腿机构在起跳过程中，点A和点B受到的力在XH轴和YH轴方向的分量。

因为弹跳腿机构相互连接，所以每个连杆都受到与之相连的其它连杆的力Fi的作用。此外，连杆可能受到扭矩弹簧Msi的作用，并可能受到外力Fti的作用。力和力矩平衡方程为：

(6)

(7)

其中r是位置向量。具体来说，Fti表示躯干的等效起飞力。为了求解FA和FB，需要计算弹跳腿在初始状态下的姿态角。在固定坐标系H-XHYH下，质心MO的矢量方程表示为

HG+GC+CB+BMO=HMO。

(8)

MO是初始状态下质心的位置点，它是已知值，因此式(8)可以重写为

(9)

其中：

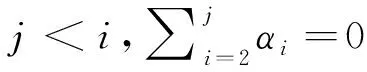
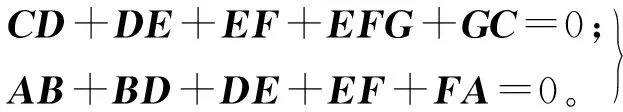
(10)

式(10)的第1个表达式可以投射到XH轴和YH轴上，可以写成：

(11)

式中：δt1是DC和BC之间的角度，可通过使用三角形BCD的余弦定理获得；θ1是连杆ED相对于连杆CG的角度。在式(11)中有3个未知数，即θ1，α3和α4。式(10)中第2个表达式可以写成：

(12)

式中：βt1=θ2-π+δt2+δt3+α5;βt2=π-2α4-2δt1+α3-θ1;θ2=π-α4-δt1-δt4;δt2是BC和BD之间的夹角;δt3是AB和AMO的夹角;δt4是CD和BD之间的夹角。

利用三角形BCD和ABMO的余弦定理可以得到δt2,δt3和δt4。θ2是连杆BD和DE之间的角度，θ3是连杆AF和连杆DE之间的角度。根据式(11)和(12),α5和α4可以由α3,θ1和θ3来表示，此时，α1和α3是未知数。

通过式(9)，可以得到弹跳腿在初始状态下的姿态；FA和FB可以通过式(7) 和(8)得到；起飞方向可用式(6)求解。在起飞过程中，6杆弹跳腿机构的质心是起飞方向线上的一系列点，并且(xMO，yMO)可替换为式(9)中的(xMOi，yMOi)。基于以上分析，弹跳机器人躯干AB的姿态可以表示为

fAB=|αt-αt0|。

(13)

式中：αt=α1-α2-α3-α4-α5。αt是AMO和XH轴之间的角度，αt0是初始状态下的αt。fAB应在允许值范围内，以保持运动稳定性，并可写为

|fAB|≤|Δα|。

(14)

式中α为最大允许角度，可根据实际情况确定。

考虑到机器人躯干姿态变化较小，机器人躯干的角加速度不随时间的增加而明显增大，接近于零，这样就能保证机构运动的稳定性。

4 机构的动力学分析

通过对确定的机构构型和各连杆的长度进行动态稳定性分析，可以确定质心的位置。考虑到各连杆的速度和加速度对动稳定性的影响，课题组采用总惯性矩来确定动态稳定性。总惯性矩可以写成：

(15)

式中：Fci和Ici分别是各连杆的惯性力和惯性矩，r为力的位置矢量，可以通过运动学分析得到;rij×Fci表示每个连杆到机器人质心的惯性力矩。

(16)

第i个连杆的质心速度可以写为

(17)

式中：vxi和vyi分别是第i个连杆的质心沿XH轴和YH轴方向的分速度，Jvi是速度系数矩阵。

此时，每个连杆的角速度和角加速度可使用以下公式获得：

v2i=v1i+ωi×Li;

(18)

(19)

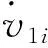
弹跳腿机构的势能包括各连杆的重力势能和弹性势能，可以表示为

(20)

式中：Δα3是关节点G的角度变化，kG是扭矩弹簧的刚度系数，mi是每个连杆的质量，hi是固定坐标系中每个连杆的质心高度。

每个连杆的长度已知，每个连杆的位置和姿态可以用α3来表示。式(20)可另写为

(21)

弹跳腿机构的总动能可以表示为

(22)

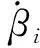
(23)

扭矩弹簧的能量损失和扭矩弹簧的阻尼与各连杆的速度有关。它可以表示为

(24)

式中CG是扭矩弹簧的阻尼。根据式(20)和式(24)，拉格朗日动力学方程可以写为

(25)

动力分析中未考虑能量损失，因为起飞过程仅为弹簧的1/4周期。此时，动力学方程可以写成：

(26)

其他关节角可用α3表示，但1阶和2阶导数的表达式非常复杂。课题组采用多项式拟合法，式(26)可被简化为

(27)

(28)

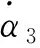
当确定了连杆、扭矩弹簧的刚度系数和机构各连杆的质量，影响总惯性矩的主要参数就是质心的位置。根据上述分析，总惯性矩I的均值和方差应该在允许的范围内。约束条件可以写成

(29)

式中：E(I)和D(I)分别是总惯性矩I的均值和方差；M(|I|)END是起飞阶段末端的惯性矩；MIE，MID和MIEnd是允许的范围值。

为了确保弹跳机构正常起跳，保持良好的动态稳定性，应满足以下约束条件：

(30)

式中：αx0和αy0是初始状态的加速度沿XH轴和YH轴的分量；E(αx)和E(αy)是平均加速度；Ax(Ax0)和Ay(Ay0)是加速度的最小值。

基于弹跳稳定性的机构设计流程如图5所示。在确定弹跳机构后，根据运动学稳定性确定各连杆的长度，并验证弹跳机构躯干姿态在起飞过程中是否满足要求。当弹跳机构不满足要求时，H点的坐标(xHi,yHi)和βHi之间的对应关系在小范围内发生变化。在此基础上，确定弹跳机构的质心位置，使总惯性矩的均值和方差满足机器人正常起飞的约束条件。

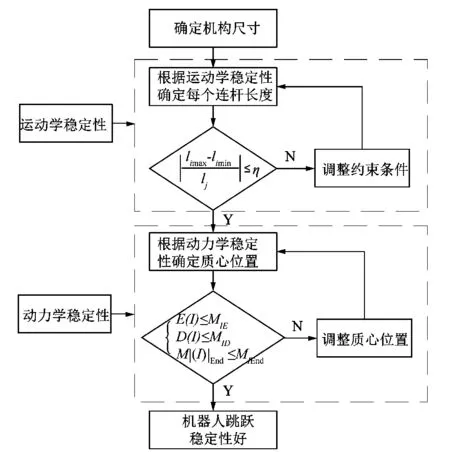
图5 基于跳跃稳定性的机构设计流程图Figure 5 Flow chart of mechanism design based on jumping stability

在运动学和动力学稳定性分析的基础上，进行了综合优化分析。在满足要求的前提下，将各连杆的长度参数和质心位置调整到较小范围内，式(14)和式(29)使其综合稳定性得到优化，目标函数可以表示为

Y={|fAB|E(I)D(I)M(|I|)END}。

(31)

5 实例分析

5.1 机器人运动稳定性分析

假设连杆BC和CD的夹角γ1=47°，β4变化范围为25°～63°，弹跳机构的质心相对位置定义为a=b=AB，扭矩弹簧的刚度系数为0.025 N·m/rad。6杆弹跳腿机构各个连杆长度如表1所示。杆弹跳腿机构起飞过程中初始、中间和最终状态如图6所示。

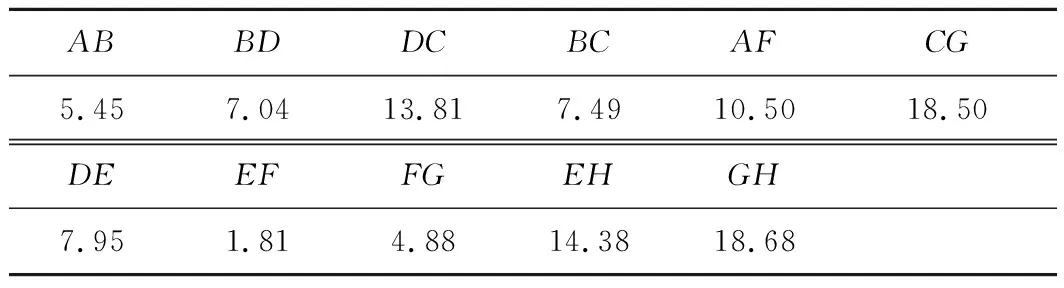
表1 6杆弹跳腿的机构参数Table 1 Mechanism parameters of six bar leg jumping mm

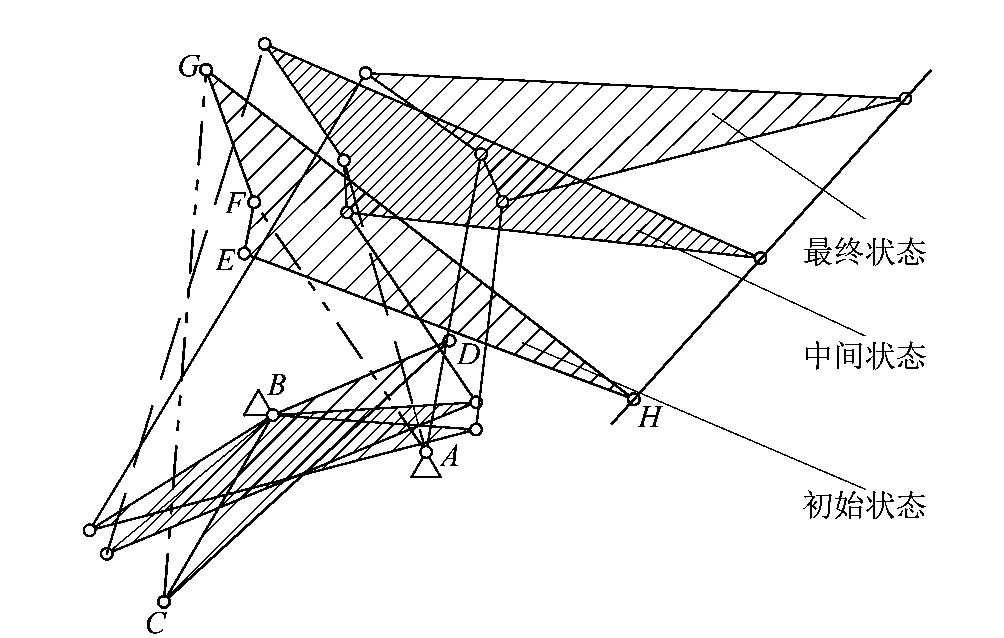
图6 弹跳腿机构起跳过程Figure 6 Take off process of spring leg mechanism

6杆弹跳腿机构中连杆HG和GC的初始状态与最终状态的角度变化约为61.51°，在起跳过程中，尖端轨迹H点始终在一条直线上。

根据式(5)得到弹跳腿机构的起飞方向角为42.55°，弹跳腿机构所带动的躯体旋转最大旋转角为0.29°，此时β4的变化范围为32.26°～58.97°，表明机器人在起飞过程中是很稳定的，γ1和β4的选择对机构参数运动性能影响不大，说明了初值选择的可行性。

5.2 机器人的动态稳定性分析

假设运动坐标系Ot-XtYt的坐标原点与连杆AB的中点重合，Yt轴的方向与连杆AB重合并指向A，Xt轴的方向垂直于Yt轴的方向如图4所示。躯干质量为0.15 kg，弹跳腿各连杆质量为0.04 kg。

对于约束条件下的优化问题，采用MATLAB中的fmincon函数对此问题进行求解，目标函数可以写成

fm=ρ1·E′[I(xm0,ymo)]+ρ2·D′[I(xm0,ymo)]。

(33)

式中，ρ1，ρ2表示比例系数，且ρ1+ρ2=1。具体来说，均值和方差应该是无量纲的，以确保数量级在相同的范围内。

假设ρ1=ρ2=0.5，目标函数fm的最小值和最大值分别为(0.000 3，-0.005 0) m和(0.000 6，-0.002 0) m，在此条件下，6杆机构弹跳腿机构起飞过程中总惯性矩的变化如图7所示。当质心目标函数fm对应最小值时，总惯性矩I在0附近上下变化，机器人机构起飞结束时fm对应的数值接近于零。当质心目标函数fm取最大值时，总惯性矩I有较大的浮动，所以此6杆弹跳腿机构在质心目标函数fm取最小值的时候有很好的动态稳定性。

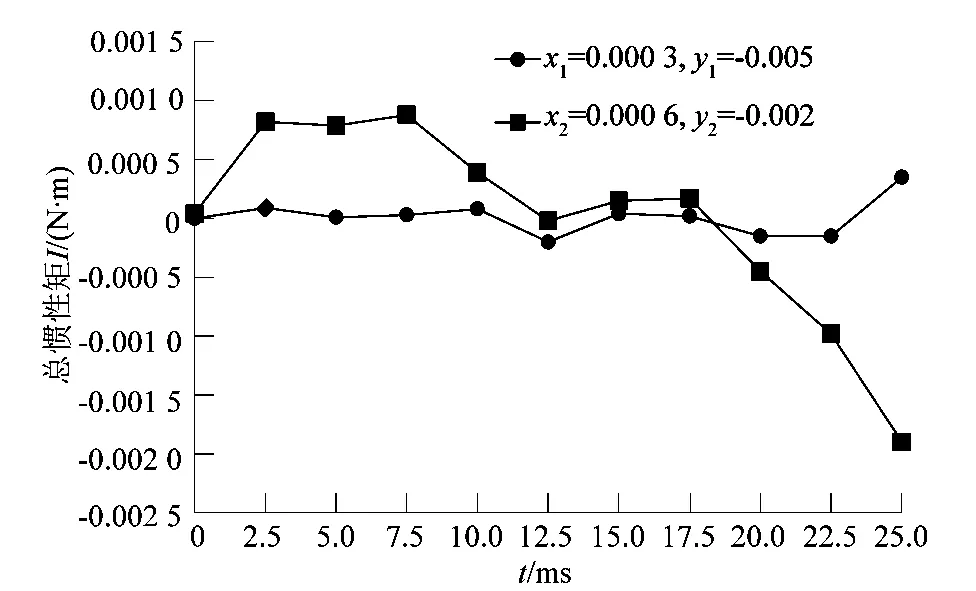
图7 起飞过程中总惯性矩的变化Figure 7 Change of total moment of inertia during take off

6 结论

1) 根据蝗虫的腿部结构，课题组提出了一种基于弹跳稳定性的6杆弹跳腿机构。

2) 课题组运用闭环矢量方程法对6杆弹跳腿机构进行运动学稳定性分析，使用躯干的姿态作为目标函数，且基于多目标标优化方法确定单自由度跳跃腿的各个连杆尺寸公式。

3) 针对6杆弹跳腿机构的动态稳定性，课题组利用总惯性矩的方法，建立了弹跳腿机构的动力学模型，求出了确定机构的质心位置的方法，以此反映6杆弹跳机构在起飞阶段的稳定性。

4) 课题组对6杆弹跳机构的初始条件赋值，进行计算验证，结果证明此弹跳机构具有良好的稳定性。