基于混合算法的航天器轨道规划方法

刘东兴，周 旭

(中国电子科技集团 第54研究所，石家庄 050081)

0 引言

近年来，在轨服务技术作为一项新兴技术受到较多关注，在维护空间在轨目标(如在轨航天器、空间碎片)方面应用频率较高。在轨服务技术可以分为在轨维护、在轨组装、在轨救援、在轨加注、在轨监测和辅助变轨等6类。从原理上讲，任何种类的在轨服务，都是一个轨道规划和优化的空间目标交会过程，即服务航天器进行轨道机动和规划，逼近目标航天器，进而完成在轨服务[1-7]。

常见的路径规划问题是指在有障碍物的工作环境中，依据某些优化准则(如能量消耗最少、路程最短、任务时间短等)，在运动空间中寻找一条从起始状态到目标状态，可以避开障碍物的最优或者接近最优的路径[8]。目前全局路径规划算法有可视法、栅格法、神经网络算法、序列二次规划法等方法，这些方法各有优点，但均存在一定的局限性，容易陷入局部最优[9]。遗传算法是一种通过模拟自然选择和生物进化过程搜索最优解的方法，在求解较为复杂的组合优化问题时，具有算法鲁棒、灵活、不易陷入局部最优等优点[10-11]。虽然遗传算法使用交叉、变异等算子可以从全局角度出发搜索最优解，但是遗传算法求解时间与染色体基因等算子数目呈指数增长的关系，这对选择染色体的编码形式和遗传算法的求解效率产生较大程度的限制，同时局部搜索能力较差，易产生“超级个体”，形成早熟现象。

为此本文构建出一种混合遗传算法[12-14]，兼顾全局和局部两个角度，将遗传算法的全局搜索能力与模拟退火算法较强的局部搜索能力相结合，进行算法设计，从而使搜索得到的个体更加接近最优解。同时提高遗传算法的求解效率，避免遗传算法早熟和模拟退火算法搜索速度慢的问题。

本文搭建了航天器在相对轨道的运动模型，从而得到服务航天器从起始时刻到目标时刻绕飞小卫星的动态运动模型。在此动态环境模型的基础上对混合遗传算法进行设计，通过仿真实验证明了该算法在动态环境中轨道规划的有效性，并且算法求解效率远高于标准遗传算法。

1 问题描述

若干个小卫星围绕目标航天器进行相对运动时，服务航天器穿过小卫星绕飞区域与目标航天器交会，进行在轨服务。为了避免与小卫星发生碰撞或相互影响，服务航天器要与小卫星要保持一定的安全距离。综上，在考虑路径安全、任务时间、燃料消耗、总路程等约束条件后，进行轨道路径规划，寻找一条服务航天器到目标航天器的最优机动轨道路径。

2 轨道动力学模型建立

为便于研究和描述服务航天器、小卫星、目标航天器的位置，当两个航天器距离较近时，可以假定其中一个航天器是固定不动的。如图1所示，建立以目标航天器质心为原点的航天器本体轨道坐标系(相对轨道参考坐标系)[15-16]。

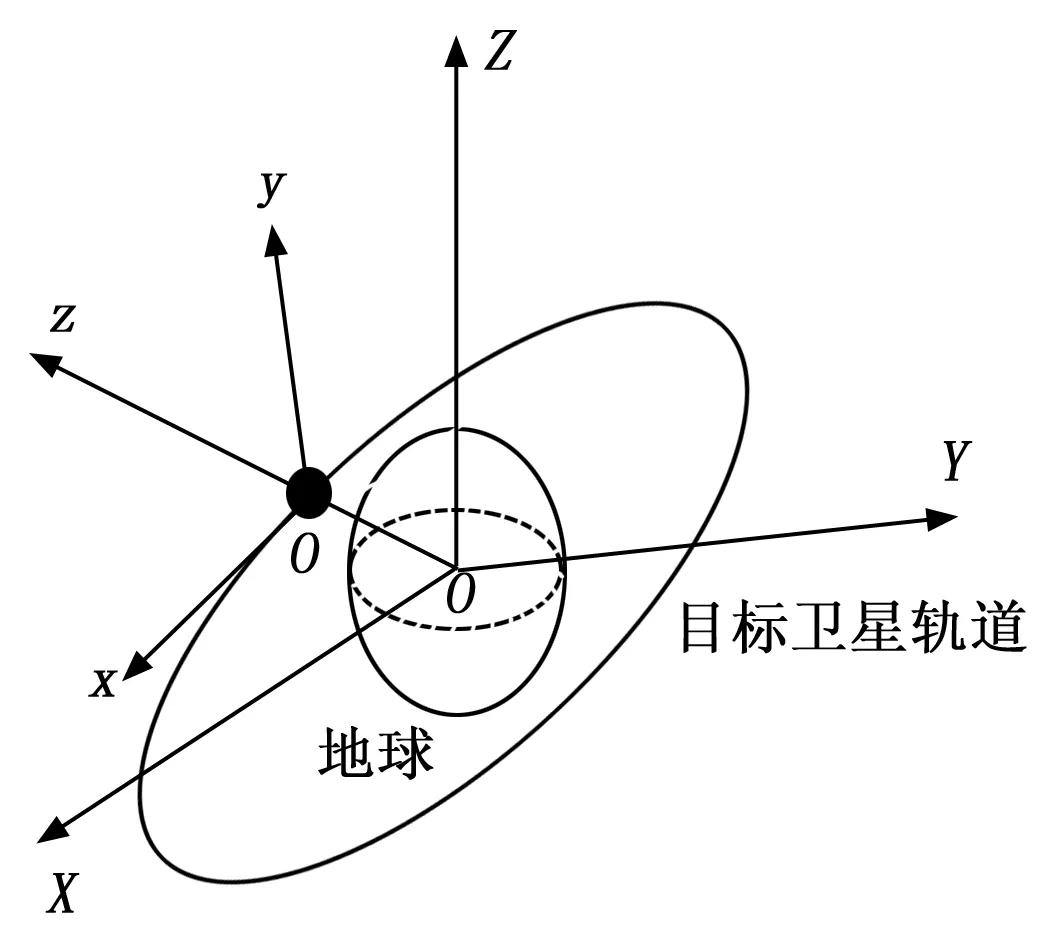
图1 航天器本体轨道坐标系

在圆形轨道中，相对运动方程就是希尔方程：

(1)

在式(1)中，ω=2π/T是圆形目标轨道的角频率，mc是服务航天器的质量。

服务航天器的运功会收到加速度γx,y,z=Fx,y,z/mc的影响。方程组(1)是线性微分方程组，可以通过拉普拉斯变换求解。因为服务航天器和目标航天器之间的距离与它们距离地球中心的距离比较小，在这一条件下，W.HClohessy和R.S.Wiltshire从希尔方程中导出了相对运动方程的线性解(W.HClohessy & R.S.Wiltshire 1960)。为了简化对各种轨道模型的讨论，假定推进机具有脉冲特性，即速度变化是阶跃的，并且假定在研究的时间间隔内，γx,y,z都是常数，得出的运动方程(C-W方程):

(2)

根据C-W方程可知，若已知的初始状态及单位质量作用力，就可以通过相对轨道动力学模型，推算出任意时刻航天器(服务航天器、小卫星)在相对轨道中的位置和速度。

服务航天器通过Lambert转移实现沿各个坐标系轴方向上的轨道改变和转移。通过求解C-W方程得到：

(3)

综上,每次施加脉冲的大小可以由式(3)得出[17-19]。

3 算法设计

3.1 设计路径的编码方式

染色体编码采用简明、直观、可行性强的可变长实数形式[20]。假设服务航天器实施轨道机动的时刻分别为(t1,t2,…，tn),实施轨道机动的位置分别为(F1,F2,…，Fn),Fn是一个三维矢量，分别表示服务航天器在参考坐标系三个方向的位置，因此服务航天器每条轨道机动的路径可编码为(t1,F1,t2,F2,…，tn-1,Fn-1,tn,Fn)。

3.2 产生初始种群

随机产生N个个体(即N条路径)，每个个体记为Pj,j=1,2,…，N。个体长度l，也同样在约束区间下随机产生。为避免随机路径中的返回部分，对每个个体Pj的坐标值降序排列(F1x>F2x>…>Fnx>F1y>F2y>…>Fny,>F1z>F2z>…>Fnz)

以增加初始种群的可行性。

3.3 建立综合适应度函数

3.3.1 优化安全性

为了避免服务航天器与伴飞小卫星发生碰撞或相互影响，在任务的任意时刻应避免服务航天器与任一伴飞小卫星的绝对距离小于伴飞小卫星的安全半径。建立如下约束轨道安全性的适应度函数：

(4)

其中:

Φji为由绕飞小卫星的安全半径形成的球形安全范围；lji表示第j条轨道机动路径中服务航天器从ti时刻到ti+1时刻的相对坐标矢量；若该轨道机动路径没有穿过任一伴飞小卫星的安全范围，ηji的值赋为1，否则赋为0。如此，fit1(Pj)的值越大，该路径的安全性越高[21-22]。

3.3.2 优化脉冲变轨次数

服务航天器每次进行轨道机动都需要施加脉冲，轨道机动次数越多，施加脉冲越多，进而燃料消耗越多。建立如下约束轨道机动次数的适应度函数：

fit2(Pj)=Nj

(5)

其中:Nj表示第j条路径中服务航天器的轨道机动次数。如此，fit2(Pj)值越小，服务航天器的能量消耗越少。

3.3.3 优化总路程

在轨服务过程中，服务航天器的轨道总路程越短，一定程度上可以减少任务时间和节省燃料。建立如下约束总路程的适应度函数：

fit3(Pj)=

(6)

其中:(xji,yji,zji)表示第j条路径ti时刻服务航天器在相对轨道坐标系中的坐标；d((xji,yji,zji),(xji+1,yji+1,zji+1)表示第j条路径ti时刻至ti+1时刻的机动轨道长度。如此，fit3(Pj)的值越小表明该路径的总路程越短。

3.3.4 优化任务时间

在轨服务任务要在一定时间内完成。时间越短，特定时间内服务航天器的服务目标数量越多。建立如下约束任务时间的适应度函数：

fit4(Pj)=Tj

(7)

其中:Tj表示服务航天器沿第j条路径所消耗的时间。如此，fit4(Pj)值越小，任务消耗时间越少。

3.3.5 优化燃料消耗

服务航天器每次机动轨道方向不同，导致各个方向所需的速度变化量不同，这直接影响到燃料的消耗。若轨道路径比较平滑，则变轨所需燃料越少。建立如下约束燃料消耗的适应度函数：

(8)

其中:Δvji表示第j条路径第i次施加脉冲时服务航天器的速度变化量。如此，fit5(Pj)值越小，服务航天器第j条路径燃料消耗越少。

3.3.6 综合适应度函数

对上述各个优化目标函数运用线性函数进行归一化处理，形成综合适应度函数：

(9)

如此，fit(Pj)值越大，个体越优良。

3.4 算子设计

3.4.1 选择算子

采用轮盘赌(比例选择)的选择方式，

其基本思想是：各个个体被选中的概率与其适应度大小成正比。具体步骤如下：

1)计算每个个体适应度值fit(Pj)；

2)计算每个个体遗传到下一代种群的概率ρj；

(10)

3)产生随机数M,M∈[0,1];

4)若M满足式(11)，则第j个个体被选中；

(11)

3.4.2 交叉算子

由于染色体编码方式是可变长度编码，所以采用单点交叉的方式，如图2所示。具体操作为：

1)根据交叉概率和随机位置确定交叉的两个染色体的交叉位置；

2)进行交叉操作；

3)交叉后的染色体坐标降序排列，避免路径环绕。

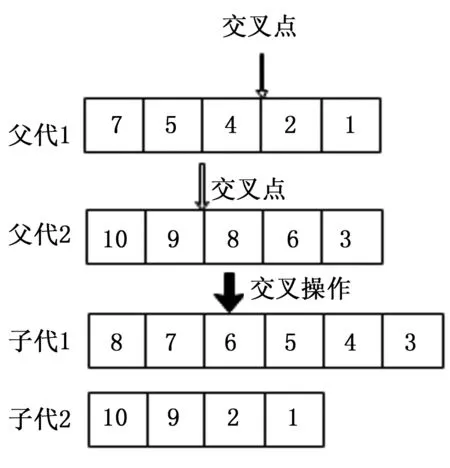
图2 染色体交叉操作示意图

3.4.3 变异算子

染色体变异采用均匀的变异方式，具体步骤如下：

1)根据变异概率确定变异的染色体；

2)随机确定进行变异基因的位置；

3)为了避免路径环绕，在变异基因前后开区间内，按照均匀分布方式随机生成变异后基因的值，完成变异操作。

3.4.4 退温函数

退温函数是模拟退火算法理论中重要一环。研究表明，降温速度越慢，获得高质量解的概率就越大，但耗时增加，极大影响了求解效率。因此，设计温度参数t，根据温度高低，控制下降速度。在温度高时快速下降，温度低时缓慢下降，达到兼顾模拟退火算法的局部搜索能力和求解的质量、效率的目的[23]。

本文算法设计的降温操作如式(12)：

tk+1=λtk

(12)

其中:t为温度参数，λ为退温速率0<λ<1。

3.4.5 Metropolis接收准则

假设问题的当前解为si，其中目标函数为g(si)；在控制参数为t时，该问题产生了新解sj，其对应的目标函数为g(si)。若g(si)≥g(sj)，则接收新解si，并将其替换问题的前解si；否则，按照式(13)对当前解si进行转换：若P>Random[0,1]，则接收新解sj；否则，保持当前解si不变。

(13)

3.5 算法步骤

混合遗传算法的流程如图3所示。

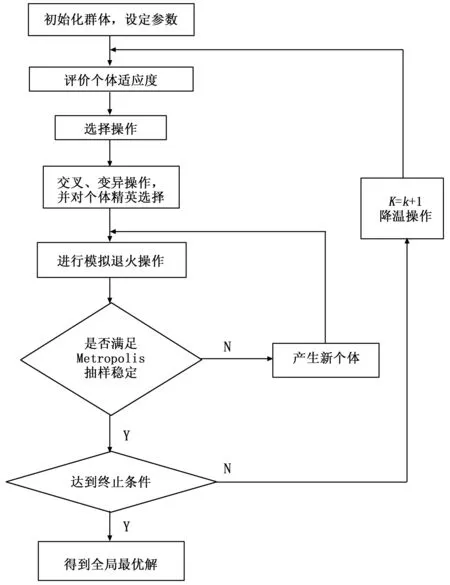
图3 混合遗传算流程图

算法步骤如下：

1)初始化群体，参数设定：种群规模N、交叉概率Pc、变异概率Pm、温度控制参数的初始值t0、退温速率λ、进化代数k；

2)计算适应度函数值，进行个体评价；

3)根据个体评价，进行选择运算；

4)对染色体进行交叉运算、变异运算、精英选择运算；

5)进行模拟退火运算，对新个体进行接受运算，以概率P为标准，直至Metropolis抽样稳定；

6)判断解是否满足算法终止条件，若满足，转步骤8)，否则转步骤7)；

7)令k=k+ 1,进行降温运算tk+1=λtk,转步骤2)；

8)输出全局最优解。

4 仿真验证

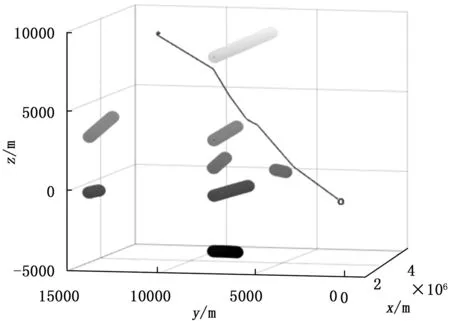
仿真场景设置：空间某目标航天器周围有8颗小卫星在其相对轨道进行绕飞，服务航天器要机动到目标航天器进行在轨服务。以目标航天器为参考，建立相对轨道参考坐标系。8个小卫星在参考坐标系中的运动模型如图4所示，目标航天器与小卫星的初始轨道参数分别如表1、表2所示。

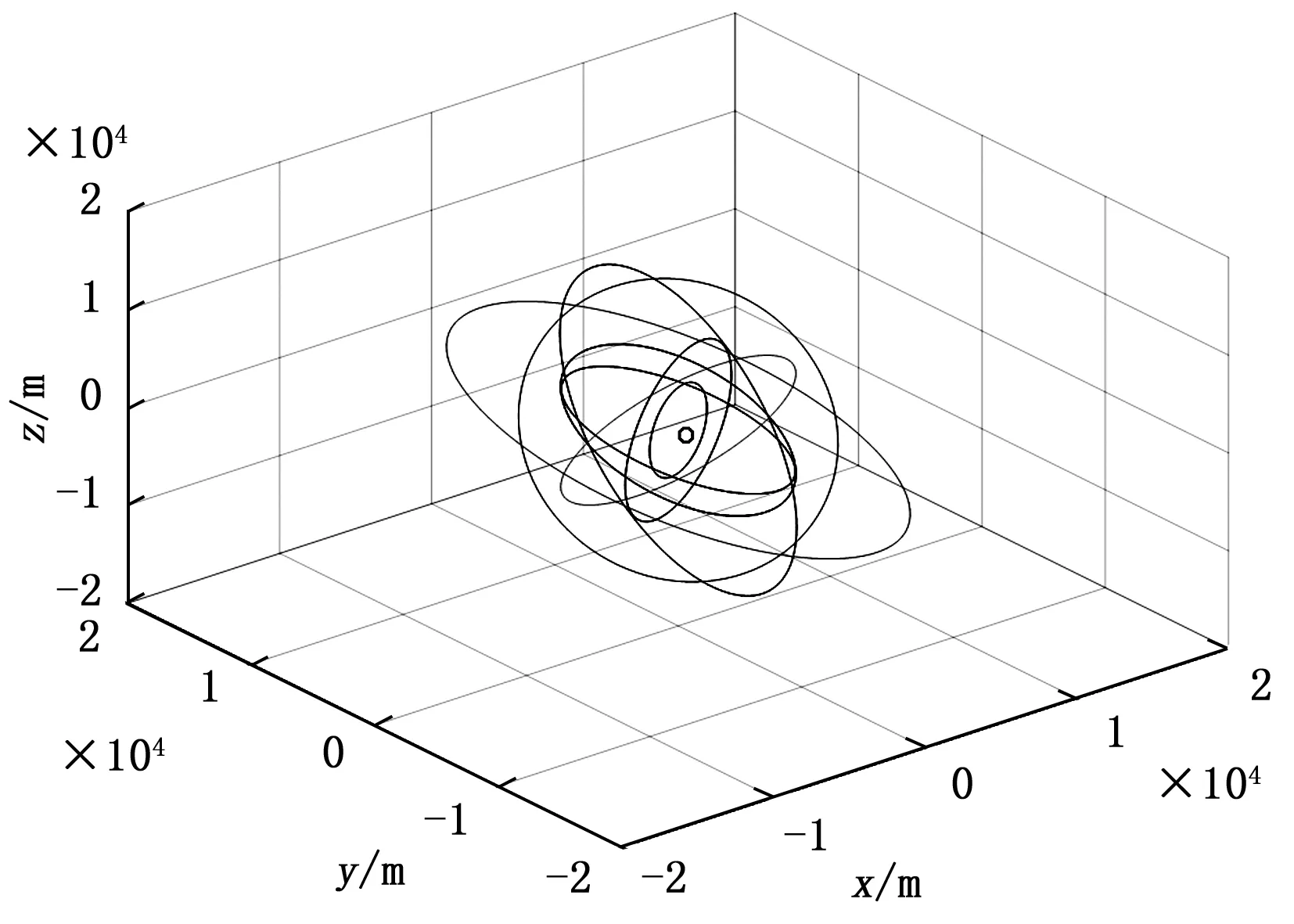
图4 小卫星在参考坐标系中的运动模型

表1 目标航天器轨道参数

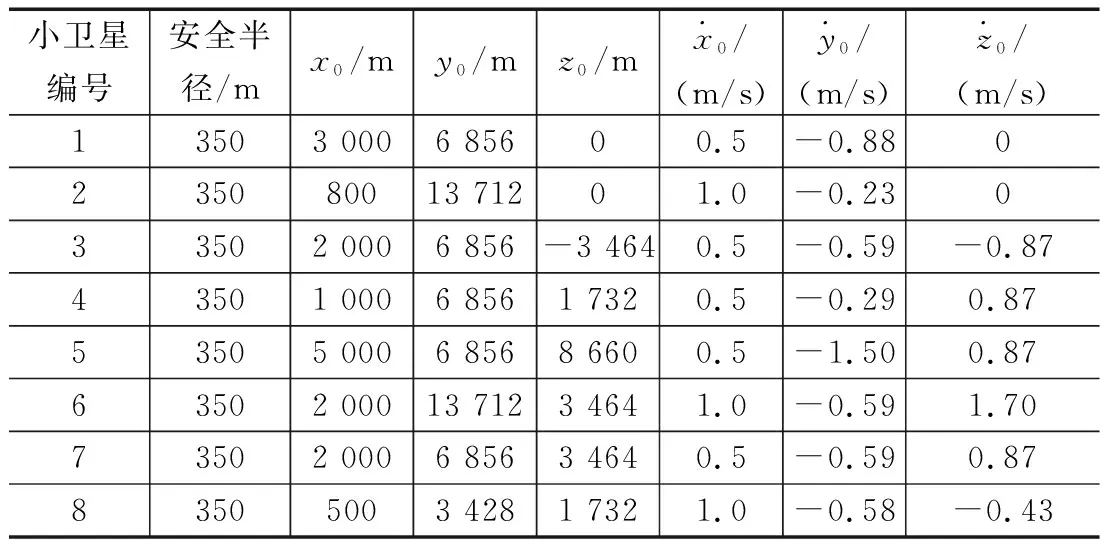
表2 编队小卫星相对轨道初始状态

仿真基本参数设置：以Matlab为程序运行平台，服务航天器在相对轨道参考坐标系中的状态起点(单位：m)设为(6 000,10 000,10 000)，目标航天器位置为(0,0,0)，初始种群规模为200，交叉概率为0.8，变异概率为0.02，精英选择比例为0.02，温度控制参数t的初始接收概率为0.12，退温速率λ=0.92。最大进化次数为1 000代；

仿真结果如图5～8所示。其中，图5～7是利用本文混合遗传算法求解结果图，用来验证本文算法的有效性；图8是在同样场景算法参数设置下，利用标准遗传算法求解的求解效率图，与图7作比较，用来验证本文提出的混合遗传算法在求解效率上要优于标准遗传算法。

图5为用混合遗传算法求解得到的最优机动轨道路径，整个过程服务航天实施轨道机动6次，脉冲施加时间及大小如表3所示。图中阴影部分为伴飞小卫星在整个任务过程中形成的球形安全区域。如图5所示，服务航天器的最优机动轨道路径与小卫星的球形安全区域没有任何一处重叠，其验证了本文算法求解结果符合轨道安全性的约束，且轨道路径相对平滑，说明服务航天器每次轨道机动幅度较小，脉冲施加较小，满足节省燃料的需求。

-：最优机动轨道路径；*：轨道起点；o:轨道终点图5 利用混合遗传算法求得的最优路径

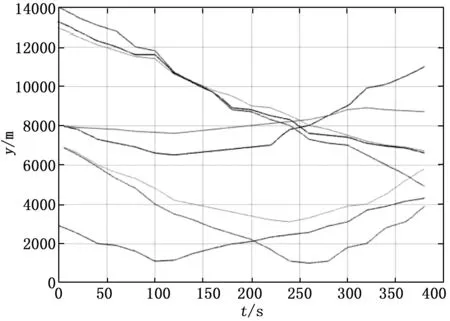
图6 最优轨道中各小卫星与服务航天器的绝对距离与安全半径的差随任务时间的变化

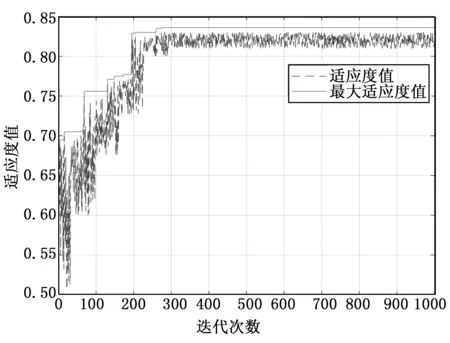
图7 混合遗传算法进化代数与适应值变化过程

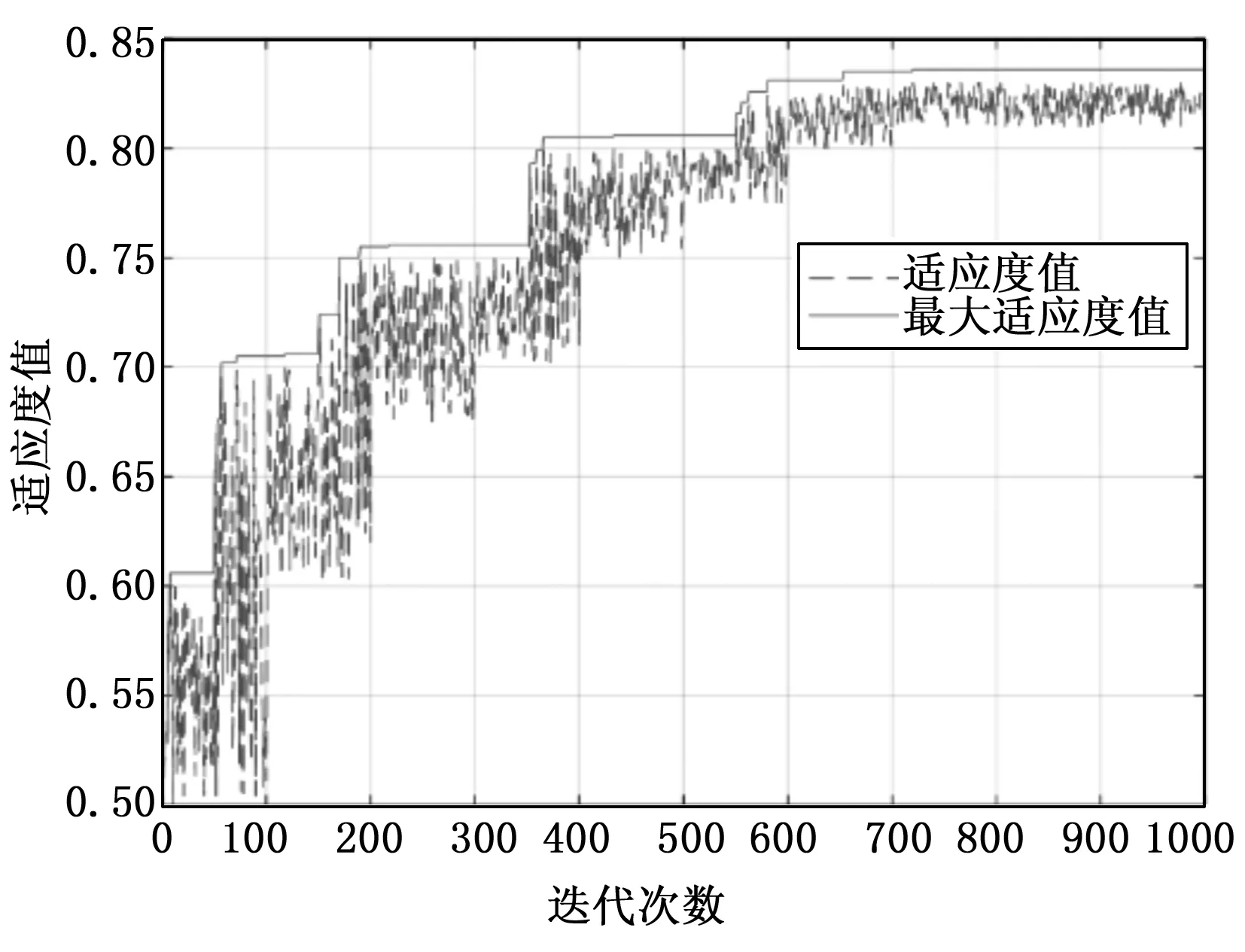
图8 标准遗传算法进化代数与适应值变化过程

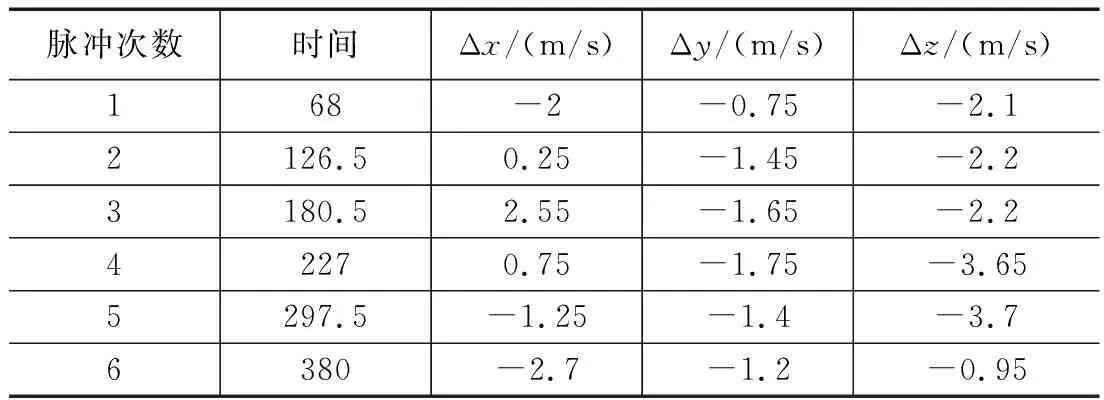
表3 服务航天器轨道机动的脉冲施加时间及大小

图6为在整个任务过程中，最优机动轨道路径中的服务航天器与各小卫星的绝对距离与其安全半径的差随时间的变化。如图所示，8个没有负值的距离差值曲线表明，服务航天器的机动轨道路径完全避开了小卫星的安全区，验证了图5的结果。并且从图6可以看出，在第380 s时服务航天器与目标航天器交会，同样场景设置下比文献[22]中的425 s提升了45 s。

图7为混合遗传算法在1 000次迭代过程中种群综合适应度函数值与当前最大适应度值的变化。如图所示，算法进化到第200代之后，最优解趋于稳定，寻找到最优机动轨道路径，验证了本文算法的收敛性与稳定性。

图8为标准遗传算法在1 000次迭代过程中种群适应值当前最大适应度值的变化。如图所示，算法进化到600代之后，最优解才趋于稳定。相同场景参数设定下，混合遗传算法求解效率比标准遗传算法提高了约两倍，求解效率提高显著。

如表4所示，与参考文献中所用的标准遗传算法求解效果相比，本文算法规划出的最优轨道路径综合性能更突出。1)路径变轨次数少；2)任务时间较短；3)本文算法求解效率上比参考文献中的标准遗传算法提高了两倍。正如表 4 所示，同样场景参数设置下用标准遗传算法，迭代到600次，才能出现稳定最优解；用混合遗传算法，算法进化到200代就出现稳定最优解；4)本文提出的混合遗传算法，先利用遗传算法强大的全局搜索能力在全局范围内寻找最优解，然后利用模拟退火算法在局部再次优化最优解，算法搜索到的最优轨道路径可靠性更佳。

表4 标准遗传算法与混合遗传算法同一场景同样参数下效果比较

5 结束语

针对在轨服务技术中空间航天器交会的轨道规划问题，本文以服务有小卫星伴飞的目标航天器为场景，通过把遗传算法较强的全局搜索能力和模拟退火算法较强的局部搜索能力整合，提出了一种混合遗传算法，来求解最优机动轨道路径。在轨道路径的安全性、可靠性、可行性和任务时间、燃料消耗、总路程等约束条件下建立综合适应度函数，并且对遗传算子、精英选择方法、退温函数、Metropolis接受准则等方面进行了设计。

算法仿真结果表明，本文提出的混合遗传算法不仅能搜索优化出一条满足安全性、可靠性、可行性和任务时间短、燃料消耗少、总路程短等约束条件下的最优机动轨道路径，并且算法的求解效率远高于参考文献中的标准遗传算法。综上，本文提出的混合遗传算法求解效率更高，最优解可靠性、可行性、综合性等更优，更适合在空间复杂场景模型下进行轨道路径规划。