基于自适应粒子群算法的多无人机混合编队技术

李 文，万晓冬,周文文

(南京航空航天大学 自动化学院，南京 211106)

0 引言

面对复杂的战场环境，单架无人机的感知、决策、攻击能力受到一定的束缚，无法满足现代战争的需求[1-2]，多无人机协同作战成为近年来无人机控制领域的研究热点。针对不同的作战任务，无人机群体需要选择合适的队形并保持队形，因此研究无人机群体在复杂环境下的编队及避障愈加必要。

目前比较成熟的编队算法有：领航跟随者法[3]、虚拟结构法[4-5]、基于行为法[6]。领航跟随者法简化了各无人机间的通信协作问题，便于形成期望的编队队形，但该方法太依赖领航者，一旦领航者发生故障会导致编队系统瘫痪而无法完成作战任务。虚拟结构法将无人机编队队形看作是一个刚体的虚拟结构，每架无人机是虚拟结构上相对位置固定的一点，编队运动时，无人机只需跟随固定点运动，优点是方便整体描述无人机编队的行为，可以进行队形反馈，缺点是编队无法建立数学模型，很难进行数学分析。基于行为法本质上是一种分布式控制方法，不受无人机群体规模的影响，但它的缺点在于无法显式地定义群体行为，难以在数学上定量描述编队特性。为了克服各个编队方法的缺陷，近年来学术界将基于行为法和Leader-Follower法相结合，提出了一种新的混合编队技术[7]，简称LFB混合编队，但通过该方法很难为每架无人机配置合适的行为控制参数。因此本文将自适应粒子群算法[8]融入到LFB混合编队技术中，提出了一种基于自适应粒子群算法的混合编队技术，简称LFBAPSO技术，通过优化各无人机的行为参数，进行了大量的仿真研究，仿真结果验证了该方法的有效性和可行性。

1 基于行为法与虚拟领航-跟随者法相结合的无人机混合编队设计

1.1 虚拟领航-跟随者法的编队技术

在无人机群体编队过程中，通常需要确定一架领航无人机，每架无人机根据领航无人机的坐标计算出自身在编队中的位置，使编队系统在整体上形成期望的几何队形。在编队执行任务的过程中，各架无人机始终保持期望的队形跟随虚拟领航无人机飞行，当无人机检测到障碍物时，无人机群能够快速切换到合适的队形，通过障碍区后各架无人机通过调整各自的位置重新保持队形前进，最终到达目的地。文中将综合各架无人机及目标点的位置选取合适的参考点作为虚拟领航无人机,以四架无人机构建菱形编队为例，将菱形几何中心作为参考点，令p(t)=[ll(t),θl(t),φl(t)]为虚拟领航无人机的几何构型向量，其中ll(t)=(xl(t),yl(t),zl(t))T为三维空间位置，θl(t)和φl(t)为虚拟领航航线的航向值。则构建无人机Ui的队形几何构型量为：

(1)

图1 无人机编队俯视图

图2 无人机编队侧视图

根据图1和图2可得编队队形几何构型矩阵如：

(2)

编队内任意无人机的三维空间位置可由式(1)中的值代入式(2)求得。考虑所有无人机飞行高度相同，因此取θ1为0。

为了达到良好的编队效果，无人机在跟随虚拟领航无人机飞行过程中要保持特定的相对位置，同时无人机的飞行速度矢量要与领航无人机一致。要求无人机编队系统在复杂的战场环境中能够实现:

1)无人机群体尽量保持期望的编队队形从起始点到达目标点。

2)无人机群体在能够依据任务需求和当前环境切换到合适的队形。

3)在执行任务过程中，编队系统具有避障功能。

4)无人机编队内部具有避碰功能，避免内部无人机之间发生碰撞。

1.2 基于行为的编队技术

文中为虚拟领航无人机设计了奔向目标和躲避障碍物的行为，针对跟随无人机设计了队形保持、避障、避碰行为[9]。将这些行为进行加权合成作为无人机的飞行向量。

1.2.1 奔向目标行为

(3)

1.2.2 保持队形行为

跟随无人机基于虚拟领航无人机在第t时刻的位置信息，计算出自己的期望队形位置(xfg,yfg,zfg)，将该位置作为跟随无人机的目标点，保持队形行为的输出方向矢量为：

(4)

1.2.3 躲避静态障碍物行为

躲避静态障碍物行为是指无人机根据探测到的实时环境信息，决定如何飞行才能避开障碍物，文中引入了逃逸角[10]的概念，让无人机检测到障碍物后旋转一定的角度避开障碍物，该行为的输出矢量如下式所示：

(5)

其中：[xd,yd,zd]T为无人机飞行速度的方向，θ为无人机为了躲避障碍物需要改变的航向角，±表示无人机向右转或向左转。

用半径分别为r和robs的圆模拟无人机和障碍物，则无人机Ui的速度v与障碍物几何中心连线lo夹角为β,如图3所示,则：

θ=φ-β，取lo=2robs=2r求得θ为45°。

图3 无人机避障示意图

1.2.4 避免与其他无人机碰撞行为

在执行任务过程中无人机不仅要躲避静态障碍物还要避免与其他无人机发生碰撞，因此为跟随无人机设计了避碰行为，其输出矢量为：

(6)

由于无人机避碰与避障原理类似，且无人机大小均相同，因此取θ为45°，当无人机左转时θ取负，右转取正。

1.3 无人机基本行为融合

无人机编队的输出行为就是对基本行为的加权合成，则跟随无人机的最终输出行为矢量为：

Vf=λ1vkf+λ2vao+λ3vau

(7)

虚拟领航无人机的最终输出行为矢量为：

Vl=λ4vmtg+λ5vao

(8)

其中：λ1～λ5分别为无人机的行为权重控制参数，将分别用经验法、基本粒子群算法和自适应粒子群算法对无人机编队进行仿真实验，确定最佳的行为权重控制参数。

2 自适应粒子群算法优化无人机行为权重参数

2.1 基本粒子群算法

所有的粒子在搜索空间中以一定的速度飞行，并通过当前搜索到的最优值来寻找全局最优值[11]。假设T维空间中每个粒子的坐标位置可以表示为xi=(xi1,xi2…,xiT)，用vi=(vi1,vi2,…,viT)表示粒子在每次迭代中的移动距离，pi=(pi1,pi2,…,piT)表示个体最优位置。设f(x)为最优化目标函数，粒子i的当前经过的最优位置如式(9)所示：

(9)

设种群中所有粒子所搜索到的最优位置为pg(t)，如下所示：

Pg(t)∈{P0(t),P1(t),…,PN(t)}

f(Pg(t))=min{f(Pi(t)),f(P2(t)),…,f(PN(t))}

(10)

在T维空间中粒子i的速度和位置根据式(11)～(13)进行更新：

vid(t+1)=ωvid(t)+c1r1(pid(t)-xid(t))+

c2r2(pgd(t)-xid(t))

(11)

(12)

xid(t+1)=xid(t)+viT(t)

(13)

式(11)中，ω为惯性权重，r1,r2为随机增量，c1为个体学习因子，c2为种群学习因子；式(12)限制了粒子速度的范围。

基本粒子群算法中惯性权重和学习因子无法随着搜索过程改变，因此算法本身具有局限性且容易陷入局部最优，算法的收敛速度难以把握。

2.2 自适应粒子群算法

文中提出的自适应粒子群算法(APSO)可以使粒子在迭代过程中惯性权重ω依据适应度的值进行调整，如式(14)所示:

(14)

式中，f为当前的适应度值，favg为平均适应度值，fmin为最小适应度值，ωmax取0.9，ωmin取0.4.

将学习因子设置为c1=c2=1.494[12]. 迭代次数为50，粒子群数目为100，粒子飞行速度范围为[-1,1],粒子的范围(要优化的行为权重参数)为[0，10]。

根据式(7)和式(8)可知，对于一个具有N架无人机的编队，需要进行优化的参数为N*3-1，定义一个1*(N*3)的矩阵，其中如果不考虑高度，可以将第三个值设为0。

定义适应度函数为：

fitness=w1D+w2F+w3C1+w4C2+w5S

(15)

其中：D表示编队无人机在执行任务过程中所行进的路径之和，F表示编队无人机的队形偏差值，C1,C2分别为编队无人机与环境障碍物、其他无人机发生碰撞的次数;S为领航无人机的时间步数(以200 ms)为一个step,文中取ω1=1,ω2=2,ω3=15,ω4=15,ω5=4。

3 仿真实验与分析

假设每架无人机都知道各自的目标位置并可以识别障碍，仿真选取4个无人机分别为UAV1,UAV2,UAV3,UAV4,一个虚拟领航无人机为V_LU,仿真选取无人机UAV1，UAV2，UAV3，UAV4保持菱形几何形状(每架无人机的位置误差在2 m范围内)，从起始位置无碰地到达同一目的地，最终以纵队降落，记录无人机从起始位置到形成编队队形的情况。实验中假设无人机具备3个基本条件：每架无人机都知道自己的最终目的地；每个无人机都具备辨别静态障碍物和其他无人机的功能；无人机不知道静态障碍物和其他无人机的位置信息，但是可以通过自身传感器检测到。仿真中设无人机的感知范围为1.5 m，无人机的避障的旋转角度为45°，无人机与静态障碍物之间的距离为1 m时开始避障，采用经验法、基本粒子群算法和自适应粒子群算法分别对无人机编队进行仿真实验，给出了仿真实验结果，对仿真实验结果进行了分析比较，确定最佳的行为参数。

基于MAPSO方法[13]和多次实验得到的结果，文中选定虚拟领航无人机的行为参数分别为λ4=2.000，λ5=1.000，四架跟随无人机的行为参数保持一致，λ1=1.000，λ2=5.000，λ3=3.000。将选定的无人机行为参数作为经验法的输入参数，依此作为参照标准，与基本粒子群算法和自适应粒子群算法得到的实验结果进行对比分析。

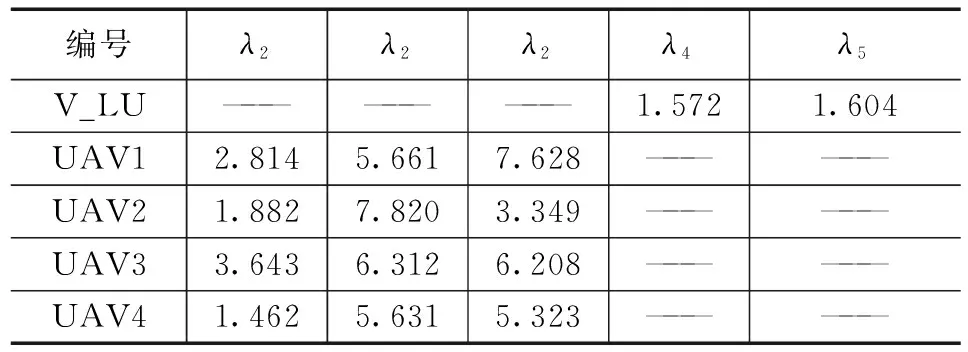
表1 基于BPSO算法得出的无人机行为权重

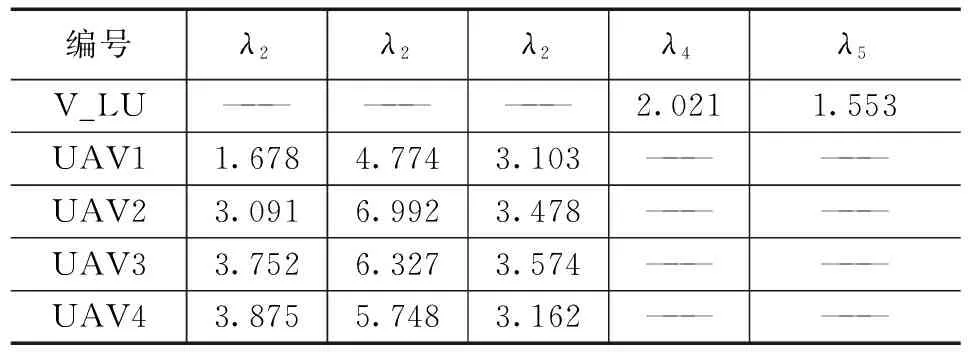
表2 基于APSO算法得出的无人机行为权重

表1和表2分别给出了基本粒子群算法和自适应粒子群算法优化后得到的最优个体的无人机的行为权重，表明自适应粒子群算法和基本粒子群算法可以求出每架无人机的最优行为权重参数，这两种算法求出的行为权重参数相比于经验法得到的行为权重参数更加精确且具有针对性。表3给出了3种方法下的无人机编队的飞行数据。

表3 3种优化方法的无人机编队飞行数据

通过对比分析表3给出的编队参数值，可以验证文中提出的基于自适应粒子群算法的无人机混合编队技术不仅缩短了飞行路径长度，并且减少了碰撞次数，在避障、避碰方面的效果更加显著，同时节省了编队时间，使各项指标都有所改善，编队准确率(综合队形误差与速度误差)达到了93.54%。

图4为基于自适应粒子群算法的混合编队技术得到的无人机编队的飞行速度矢量图，在18秒时速度曲线汇合与一处，表明无人机编队的速度达到了一致。

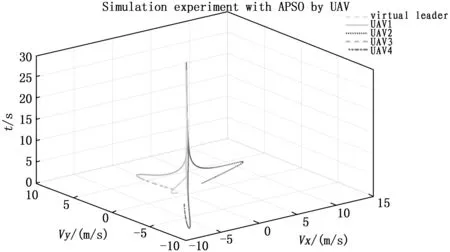
图4 编队的飞行速度矢量

图5和图6为无人机编队飞行速度误差随时间变化状态图，表明在编队队形形成的过程中无人机编队的速度误差逐渐趋向于0，验证了算法的有效性。

图5 编队飞行速度在x轴方向上的误差

图7为无人机群的初始状态图，仿真环境为50 m*50 m的密布静态障碍物的平面环境，无人机的起始位置分别为(2,36)、 (6,27)、(10,15)、(11,25)，障碍物位置任意，目标位置为(45,31)。图中白色区域为可飞行区域，灰色区域表示无人机，黑色区域为障碍区，亮灰色区域表示编队最终目的地。

图7 无人机群初始状态

图8为无人机编队躲避静态障碍物图，无人机编队检测到前方为狭窄障碍区域时切换为直线形进行避障。

图8 无人机编队避障

图9为无人机编队切换菱形队形图，表明无人机编队在避障结束后切换为菱形飞行，直至到达目的地。

图9 编队切换菱形队形

图10为编队结束状态图，表明当编队无人机检测到即将到达目的地时无人机群体切换成直线形，所有无人机到达目的地后依次降落。

图10 编队结束状态

仿真实验结果表明，无人机群体可以从初始位置到达目标位置形成菱形，并在后继执行任务中很好地保持了队形，当无人机检测到障碍时编队队形变换成直线形，绕过障碍后编队又恢复菱形继续朝目标前进，最终到达目的地，编队切换为直线形依次降落。上述实验仿真结果证明了无人机混合编队在遇到障碍避障的反应能力和编队的快速变换能力，可应用于多无人机战场环境中。

4 结束语

文中将自适应粒子群算法应用到基于行为法和虚拟领航者法相结合的混合编队技术中，分别为虚拟领航无人机和跟随无人机设计了基本行为并通过自适应粒子群算法优化各架无人机的行为参数，使无人机编队具有良好的编队效果。上述实验仿真结果充分验证了文中提出的基于自适应粒子群算法的无人机混合编队技术的可行性。