基于异构平台的通量分裂格式性能研究

梁正虹，黄 俊，刘志勤，陈 波，杨 茂

(西南科技大学 计算机科学与技术学院，四川 绵阳 621010)

0 引言

计算流体力学(CFD,computational fluid dynamics)通过数值求解流体动力学控制方程，获取各种条件下的流动数据和作用在绕流物体上的力、力矩和热量等,从而达到研究各种流动现象和规律的目的。CFD是涉及流体力学、计算机科学与技术、计算数学等多个专业的交叉研究领域[1]。在航空航天领域，CFD已成为获取高超声速飞行器气动力和气动热数据、开展高超声速流动基础科学问题研究的三大手段之一[2]。

对于高超声速流动，保持格式的迎风特性对于计算结果十分有益。迎风格式主要沿着矢通量分裂(FVS, flux vector splitting)和通量差分分裂(FDS,flux difference splitting)两个路线发展。FVS的典型格式有Steger-Warming[2]和Van Leer[2]；FDS最具代表性的是Roe[2]格式。FVS将对流项通量按其特征值的正负进行分裂，稳定性好但数值粘性较大；FDS通过近似求解Riemann问题获得控制单元通量，计算量较大且需要引入熵修正，增大了数值粘性[3]。20世纪90年代，Liou和Steffen提出兼具FVS和FDS优点的AUSM[4](advection upstream splitting method)格式，经过20多年的发展，其衍生格式已成为目前航空航天领域应用最广泛的格式之一。

CPU/GPU异构并行架构是当今构建大规模计算集群的主要架构之一，计算机技术的快速发展给CFD高性能计算领域带来前所未有的机遇与挑战。美国国家航天局(NASA)预测，21世纪，高效能计算机和CFD技术的进一步结合将给各类航空航天飞行器的气动设计带来一场革命[5]。近十年来，国内外专家学者通过CPU/GPU异构平台加速CFD应用，取得一系列重要成果。D.A.Jacobsen[6]等成功地将CFD应用从单GPU扩展至多GPU和集群；M.Aissa[7]等在GPU平台上开展了基于结构网格的显格式隐格式加速性能研究；Y.Xia等[8-9]研究结构网格、非结构网格和混合网格在GPU上实现的差异；I.C.Kampolis等[10]分析了GPU架构单精度和双精度对仿真结果的影响。马文鹏[11]等在GPU上实现了基于混合网格的非定常流动问题的求解；刘枫[12]等建立了基于MPI+CUDA的异构并行可压缩流求解器；李大力[13]等在天河2超级计算机上实现了GPU的高阶格式隐式求解。国内外学者在CPU/GPU异构平台上开展大规模CFD并行计算做出大量相关工作，但鲜有文献对不同通量分裂方法的典型格式在CPU/GPU异构体系下的性能做出具体分析。

本文以一维激波管问题为算例，给出通量分裂方法的典型格式在GPU架构下的具体性能分析，为进一步在CPU/GPU异构平台上开展大规模CFD工程应用提供有益的指导和参考。

1 通量分裂方法

在进行CFD数值模拟中，差分格式的构造是CFD的关键之一。迎风类差分格式是从20世纪80年代开始兴起，在构造时就体现了方程在波动和流量等传播方向上的物理特性，与中心差分格式相比具有表现具体流动物理特征的天然优势。发展至今，各种迎风类格式已经成为工程界和学术界研究的主流。根据对方程物理特性的不同表现形式，迎风格式也可大致分为矢通量分裂(FVS)方法和通量差分分裂(FDS)方法。

1.1 矢通量分裂

FVS(flux vector splitting)方法，最初发展于20世纪80年代，它根据相关传播速度的正负对通量项进行分裂。矢通量分裂方法，简单、高效、鲁棒性高、理论上不会出现非物理解，并且具有较强线性波(如激波等)捕捉能力。根据不同的分裂方式，构造出不同的FVS格式，最具代表性是Steger-Warming格式和Van Leer格式。其中由于Van Leer格式在驻点、声速点等特征值变号的附近区域可以光滑过度，从而在航空航天工程领域得到广泛应用。

一维欧拉方程进行矢通量分裂：

(1)

Van Leer格式通量分裂表达式：

Ma>1:

F+=0,F-=F

(2)

|Ma|>1:

(3)

Ma<-1:

F+=F,F-=0

(4)

1.2 通量差分分裂

通量差分分裂是迎风类格式的另一条发展路线，FDS以Godunov方法为基本思路，但与Godunov精确求解黎曼问题的方法不同，FDS近似求解黎曼问题，其对激波和接触间断都具有很高的分辨率。根据不同的解近似黎曼问题的方法，构造不同的FDS格式，最具代表性的是Roe格式。

将一维守恒形式欧拉方程表示为：

(5)

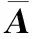
(6)

Roe格式通量表达式为：

(7)

其中：下标(i+1/2)为控制体表面；下标L和R为控制体表面左右两侧。

1.3 AUSM分裂方法

在20世纪90年代初，Liou和Steffen利用不同格式的优点，提出AUSM(advection upstream splitting method) 格式。它结合了矢通量分裂在非线性波捕捉上的鲁棒性和通量差分分裂在线性波上的高分辨率。从格式构造来讲，AUSM是Van Leer格式的一种改进，但从其耗散项来分析，它是一种FVS与FDS的复合格式。目前，AUSM格式经过20多年的发展，已经衍生出一系列格式。本文以高超声速领域使用较广的AUSMPW+格式为基础，研究其在GPU硬件架构下的计算性能。

AUSMPW+格式具体表达式：

(8)

(9)

(10)

(11)

(12)

(13)

(14)

式中，f为基于压力的权函数，具体形式参考文献[2]。

2 Riemann问题与计算模型

2.1 Riemann问题

Riemann问题是CFD的经典算例，它包含了CFD中的各种间断(膨胀波、激波及接触间断等)问题，对于这些间断问题的求解一直是CFD发展的难点和核心问题。Riemann问题具有精确解，可以验证数值方法的精度，由此，一般差分格式都是建立在求解Riemann问题基础之上，之后再向多维扩展。

一维Riemann问题实质上是激波管问题。激波管是一根两端封闭、内部充满气体的直管。直管中一层薄膜将管隔开，在薄膜两侧充满均匀理想气体，薄膜两侧气体的压力、密度不同。当时，气体处理静止状态。当时，薄膜瞬时破裂，气体从高压端冲向低压端，同时在管内形成激波、稀疏波和接触间断等复杂波系。激波管问题初始条件简单，计算网格只需一维等距划分，计算过程不引入复杂处理、网格质量等非格式因素的影响。

激波管示意图如图1所示。

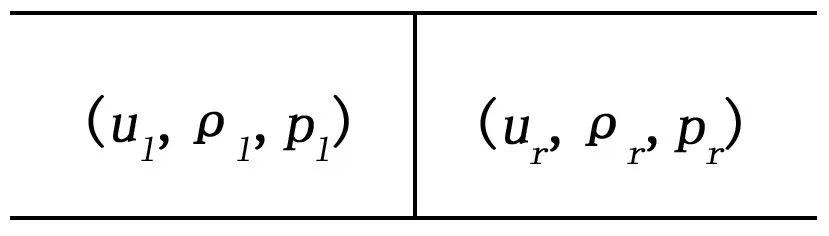
图1 Sod激波管问题

对于本次计算问题，计算区域为X=(0,1)，边界条件在计算区域边界处取内点的一阶插值，初始间断分布为：

(ul,ρl,pl)=(0,1,1) 0≤x<0.5

(ur,ρr,pr)=(0,0.125,0.1) 0.5≤x≤1

2.2 控制方程

不考虑热源、热传导和体积力的影响，控制方程采用一维非定常欧拉方程的守恒形式：

式中:

(15)

补充理想气体状态方程使方程组封闭：

(16)

3 基于GPU的一维欧拉求解器

3.1 CPU/GPU并行模式

GPU不是一个独立执行的平台，GPU的工作需要CPU协同，在异构计算体系中，CPU与GPU通过PCIE总线连接在一起协同工作。CPU称为主机端(host)，GPU称为设备端(device)。CPU可以实现复杂的逻辑运算，但其计算单元较少；与此相反，GPU包含大量的计算单元，相较于CPU，GPU线程是轻量级的，上下文切换开销小，比较适合执行大规模数据并行的计算密集型任务。

GPU的核心组件是流多处理器(SM,streaming multiprocessor)，SM的核心组件包括CUDA计算核心、共享内存、寄存器等，SM可以并发执行数百上千线程，并发能力依赖SM拥有的资源数。GPU执行模式为单指令多线程(SIMT,single instruction multiple thread)模式， 即一个warp(通常为32个线程)执行同一条指令，遇见条件分支时，按分支顺序执行。

本文采用CUDA对GPU进行编程，CUDA 是NVIDIA公司推出的通用并行计算架构。一个典型的CUDA程序包括Host端和Device端两部分代码，Host代码在CPU执行，Device代码调用内核在GPU上执行。 典型CUDA程序的执行流程如下：

1)分配host端内存，进行数据初始化；

2)分配device端内存，将host数据拷贝至device上；

3)调用CUDA核函数在device上执行运算；

4)将device上计算结果拷贝至host；

5)释放device端和host端内存。

3.2 基于CPU/GPU的CFD并行算法

图2展示了一个典型的CFD算法流程，CFD程序主要包括了3个关键部分，时间步长计算，算法核心求解步计算和进行边界条件处理。其中，算法的核心求解步占用了CFD计算的大量时间。在CPU/GPU异构并行计算体系如何分配这三大部分将会决定整个求解器的性能。

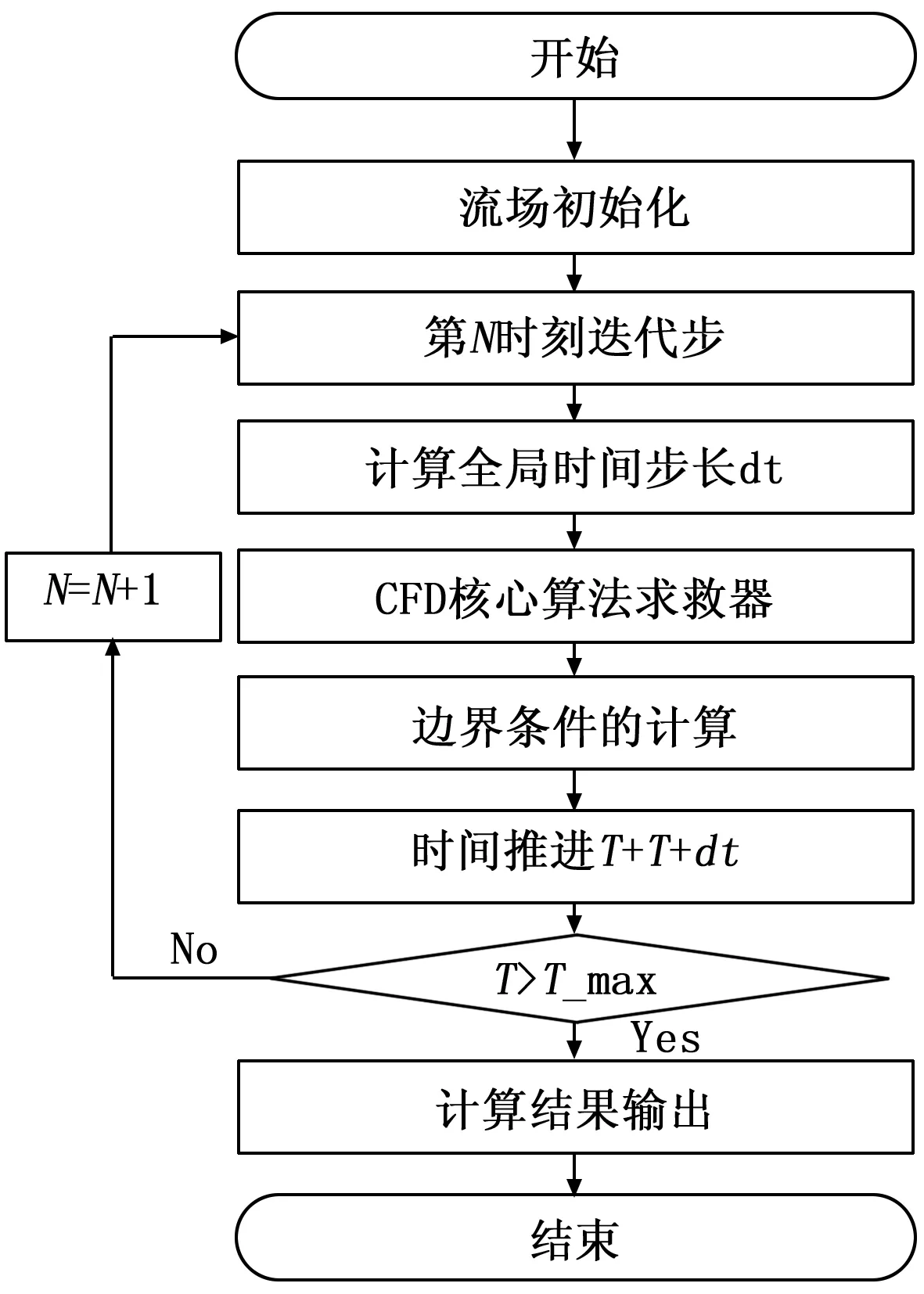
图2 CFD算法流程图

本文将时间步长计算分为两部分，全局时间步长的计算和系统迭代时间步的计算。迭代时间步的计算涉及到复杂的逻辑判断和循环过程。鉴于此，将迭代时间步的计算置于CPU上执行。针对如何分配CFD程序三个关键部分的计算，本文考虑两种并行算法。

算法一：对于算法核心步骤的计算，需要将流场变量u从CPU传输至GPU(主机端到设备端)；而边界条件的计算，需要用到核心算法求解器计算过后的流场变量d_u(在GPU上分配的变量数组之前添加d，以区别CPU上具有相同功能的数组)，d_u需要从设备端传输至主机端。图3给出了算法一的示意图。在本模式中，整个计算过程只有核心求解器的计算置于GPU，其余部分全部交由CPU完成。

算法二：图4给出了模式二的示意图，全局时间步长的计算、核心算法求解器的求解和边界条件的处理全部置于GPU上执行，最小化CPU和GPU之间的数据传输。主机流场变量u和d_u分别仅在循环之前和之后传输一次，而只有声速d_a需要从设备端单向传输至主机端进行迭代时间的计算。

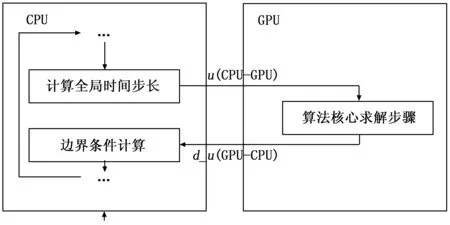
图3 并行算法一

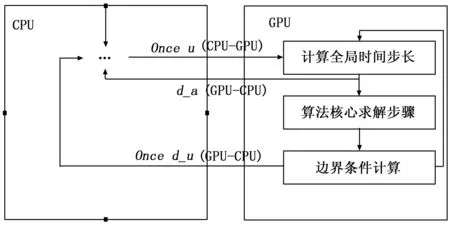
图4 并行算法二

对于GPU上的大多数应用程序，限制程序性能瓶颈的是CPU和GPU之间的带宽[14-16]，而非GPU的浮点性能(单块GPU RTX-3090的浮点性能已达到35.7 TFLOP/s)。此外，在许多内存绑定CFD程序中，带宽达到极限，浮点性能远远小于GPU峰值的情况经常出现。综合考虑，本文采用算法二进行求解器实现。

4 算例分析

本文建立一维欧拉求解器，对Sod激波管问题进行计算，分析了通量分裂方法的典型差分格式在CPU/GPU异构并行体系中的计算性能。本文主要是针对格式本身性能进行研究，故Van Leer格式、Roe格式和AUSMPW+格式均采用一阶计算，计算精度为双精度。

4.1 GPU计算结果

测试采用的CPU为INTEL I7处理器，8核，主频为3.2 GHz，主机内存32 GB，GPU为NVDIA GTX 1 660 super，拥有1 408个CUDA计算核心，单精度浮点性能约5 300 GFLOP/s，双精度浮点性能约170 GFLOP/s。计算取时结果。

t=0.2时刻，激波管内流场结构如图5所示。激波管内流场被分为A、B、C、D共4个区域，A区域和D区域中波未传播，未受到扰动干扰，保持着流动初始状态；B区域为膨胀波扫过后的区域；C区域为激波扫过区域。B区域和C区域以一个接触间断分开，B、C两区域压力相同、密度和温度不同。

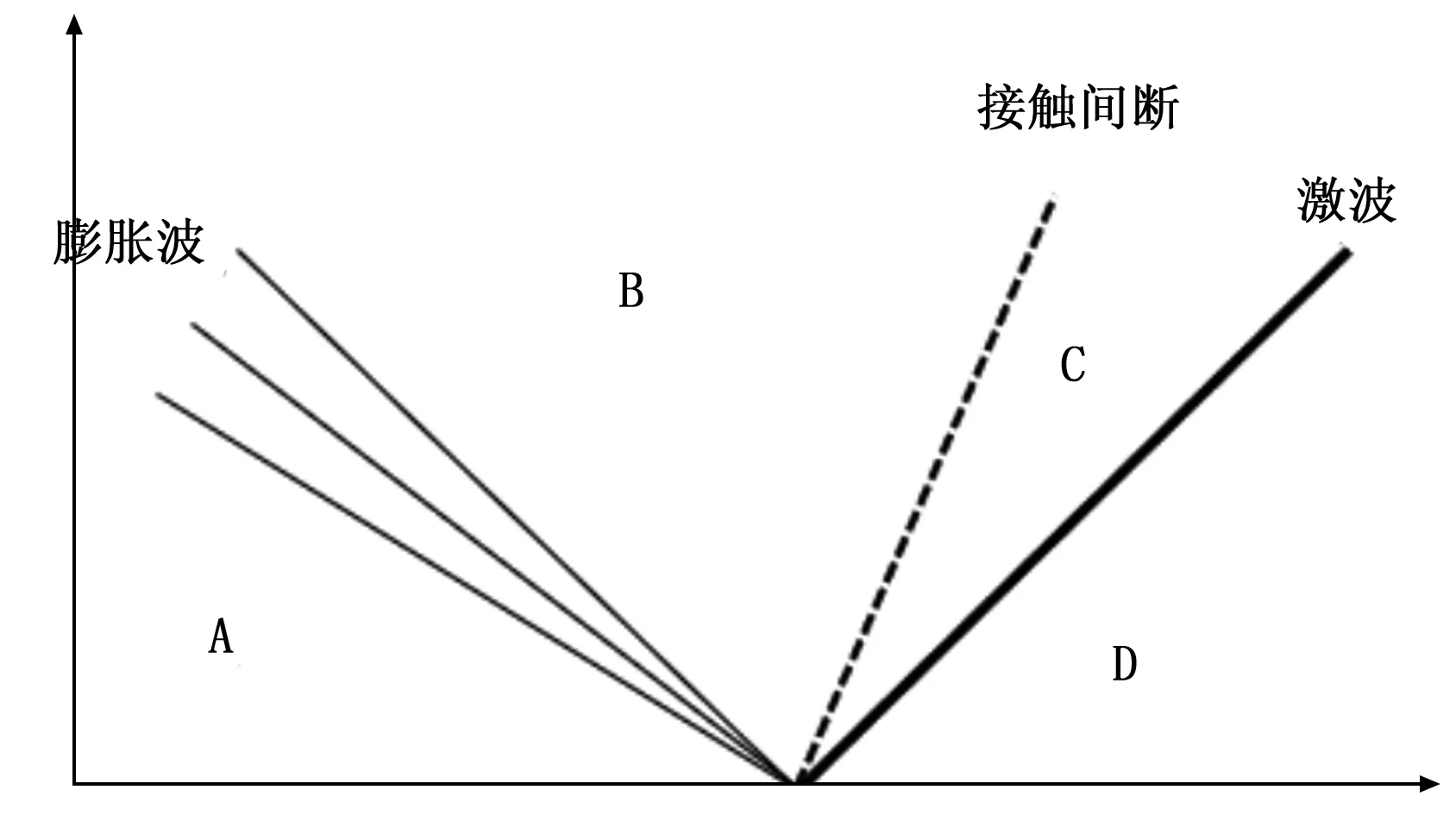
图5 t=0.2波系结构图

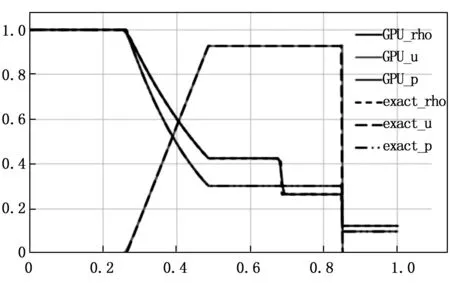
图6 Van Leer计算结果

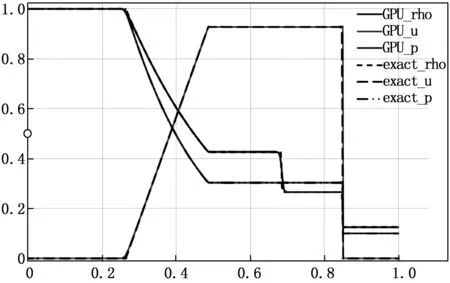
图7 Roe计算结果

图8 AUSMPW+计算结果

图6～8分别展示了t=0.2时，3种格式在10 000个网格点下的计算结果。如图所示，3种格式都能清晰地分辨出所求时刻流场的波系结构。气体压力差产生的激波从x=0.5处向右传播，t=0.2时刻传播至x=0.85附近，产生速度、密度和压力的跃迁；x=0.25和x=0.5之间3个变量缓慢变化，形成膨胀波；x=0.68处，速度和压力不变，密度产生跃迁，为接触间断。通过与精确值对比，3种格式在CPU/GPU异构体系下得出合理且可用的计算结果。

4.2 格式效应分析

图9展示了t=0.2时刻，3种格式在256网格点下，流场的密度分布，为了便于比较格式对流场波系的分辨情况，给出t=0.2时刻的流场密度精确解进行比较。可以看出，本文所采用的3种格式在256网格下都能表述所求时刻间断分布。格式本身对于间断的捕捉有差别，图10展示了激波附近局部放大图， Roe 激波分辨率最高，AUSMPW+与Roe激波分辨率相当，Van Leer激波分辨率低于Roe和AUSMPW+。值得注意的是AUSMPW+格式，它是一种FVS和FDS的复合格式，兼有FVS的计算效率和FDS的间断高分辨率。计算结果表明，它在间断前后表现出与Roe格式相当的性能，同时又兼有与Van Leer格式相当的计算效率。

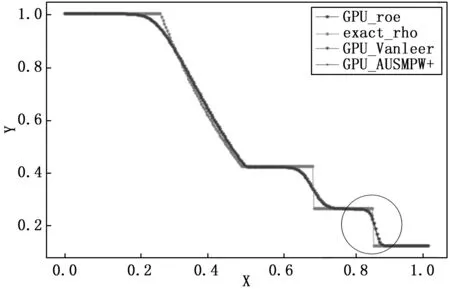
图9 3种格式计算对比

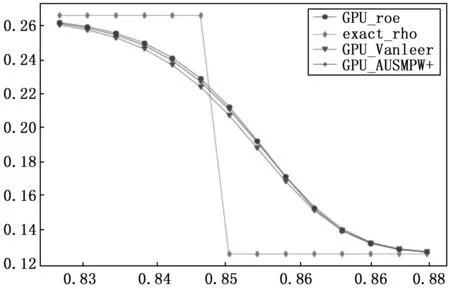
图10 激波局部放大图

4.3 格式加速性能分析

本文研究格式本身在CPU/GPU上性能分析，加速比定义为算法核心求解步在CPU运行时间与相应GPU时间的比值，为排除额外因素干扰，时间步长取固定值0.000 001。

表1为3种典型格式在CPU执行时间(100、1 000、10 000共3种网格计算规模)，由计算结果可知，Van Leer计算效率最高，AUSMPW+计算所需时间略高于与Van Leer，Roe消耗时间最多。表2展示了3种格式在GPU执行时间。在本文的计算的网格规模中，GPU硬件体系结构上，Van Leer计算效率稍高于Roe和AUSMPW+。表3体现了3种格式的加速比，在网格规模较小时，GPU计算时间大于CPU计算。主要原因是网格规模小，无法体现GPU众核体系进行大规模计算的优势。加速比由高到低依次为Roe、AUSMPW+、Van Leer。其影响因素有：Roe格式构造中，需要对矩阵进行计算，其计算量远大于Van Leer和AUSMPW+，而且Roe没有条件语句分支，控制流指令较少，运行中warp分支少，格式适用于GPU单指令多线程运行模式，故Roe加速效果最好；AUSMPW+和Van Leer两种格式存在大量条件分支，不利于GPU运行模式，影响了加速效果；AUSMPW+加速优于Van Leer的原因是AUSMPW+计算量大于Van Leer(从格式构造来看，AUSMPW+是Van Leer的改进，其计算步骤更多更复杂)。从以上分析结果来看，影响格式在异构平台的加速性能主要是格式存在的条件判断分支以及格式的运算量。

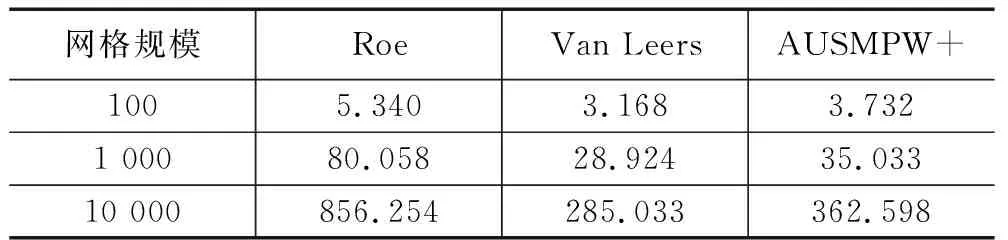
表1 CPU不同网格规模格式计算时间 s

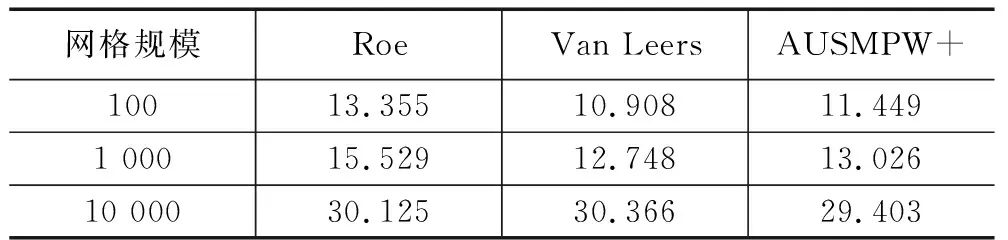
表2 GPU不同网格规模格式计算时间 s

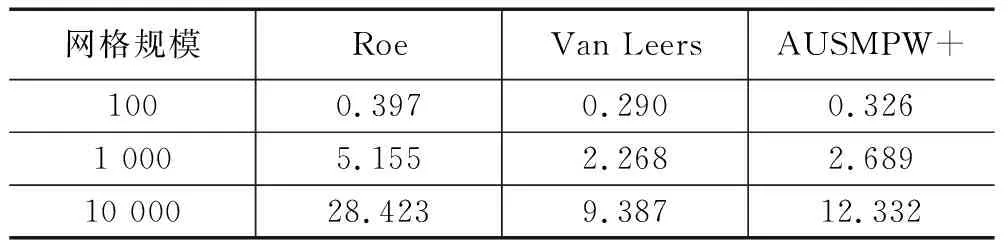
表3 格式加速比 s

5 结束语

为了研究通量分裂格式在异构并行计算平台的加速性能，本文在 GTX 1660 super上利用CUDA开发了一维欧拉求解器，并对当前航空航天领域常用的3种典型格式进行计算分析，结果表明：

1)Roe格式对流场解析效果最好，且在异构平台加速性能最高，目前应用前景最好。

2)格式构造中存在的条件分支严重影响了格式的加速性能，构造数值格式时，合理地减少条件分支，将会大大提高其在异构平台的加速效果。

本文的工作对于在CPU/GPU异构并行计算平台开展CFD算法相关研究具有一定的指导意义。