基于Tiny-YOLOV3的无人机地面目标跟踪算法设计

张兴旺，刘小雄，林传健，梁 晨

(西北工业大学 自动化学院, 西安 710072)

0 引言

随着计算机视觉技术的发展，目标对象跟踪越来越成为计算机视觉领域的热门研究方向[1-2]。近年来无人机领域的技术愈发成熟，这使得基于无人机的目标跟踪系统的实现变得相对容易，而在工业、军事等领域的应用需求也使得无人机跟踪系统的实现变得迫切。因此目前涌现了一大批国内外学者对无人机目标跟踪领域进行了深入研究。R.Gonzalo[3]等人提出了一种利用单摄像机实时检测和跟踪无人机运动目标的方法，该方法主要是通过比较人工建立的光流场和真实光流场得到一个动态像素列表，然后分组为动态对象，在时间和空间中对动态对象进行跟踪。JeongWoon等人利用目标的颜色特征对目标进行识别，并利用AR.Drone 2.0无人机实现了对一个红色椭圆图案的跟踪[4]。东南大学针对四旋翼无人机跟踪地面目标过程中出现的目标遮挡问题，设计了基于粒子滤波结合P-N在线学习的目标跟踪算法[5]。

目前关注度较高的目标跟踪算法分为两类：相关滤波和深度学习。而相关滤波选用的特征大都基于手工设计的特征，如方向梯度直方图(HOG)[6]、局部二分模式特征(LBP)[7]等。相比较大量训练数据样本学习出来的深度特征，手工设计的特征在检测的准确性上相比较深度特征差了很多[8-9]。YOLOV3[10]作为一种目标检测算法，使用卷积神经网络训练目标深度特征，最终得到目标的类别和位置，可以在兼顾速度和准确率的前提下实现单一目标的跟踪，是一种性能优良的算法。

由于目标检测算法不可避免地存在漏检问题，目标物体的丢失将会导致跟踪失败。而卡尔曼滤波(KF)作为一种顺序最小二乘逼近算法，可以从包含噪声的有限信号中预测出目标的真实值[11]。它的基本思想是：根据目标的状态方程和量测方程，建立卡尔曼滤波方程。在给定状态初值的基础上，利用目标的动态信息，采用递推方法去掉噪声的影响，从而得到目标的最优估计量。因此它可以针对目标跟踪算法某一时刻检测不到物体时对该时刻的目标轨迹进行预测，同时滤除整个目标运动过程中的噪声干扰[12-13]。

基于以上研究成果，考虑到旋翼无人机机载处理器的处理性能有限，本文采用Tiny-YOLOV3作为目标跟踪算法，通过与无人机数据的融合建立了目标跟踪模型，并结合卡尔曼滤波器进行目标轨迹预测，然后设计基于PID的旋翼无人机控制律以实现无人机对目标的有效跟踪，仿真结果表明了本文提出的算法的有效性[14]。

1 基于Tiny-YOLOV3的目标检测

1.1 Tiny-YOLOV3基本原理

YOLO[15-16]全名You Only Look Once,历经三次演变为现在的YOLOV3。Tiny-YOLOV3作为YOLOV3的简化版本，其算法的基本原理是：首先输入大小为416×416的RGB图像，通过特征提取网络后获得两个不同尺度大小的特征图，分别为13×13和26×26；然后将输入图像划分成和特征图大小相同的网格单元，图像中每个物体的中心部分所在的网格负责该物体的检测，即标注数据(ground truth)中某个物体的中心坐标落在哪个网格中，就由该网格预测该物体接着每个单元网格预测3个边界框(bounding box)；最终输出的预测图具有两个维度，即特征提取的维度，如13×13的特征图；另外的维度是深度，对于COCO数据集来说，深度为3×(80+5)。因此最终输出的特征图大小为13×13×255和26×26×255。

最终预测输出中，每个边界框需要给出一个置信度。这个置信度包含两个方面的信息，即反映网格中是否有物体以及对网格中物体的预测是否准确。因此置信度的定义如下：

(1)

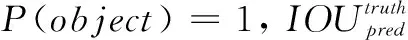
(2)

此外，每个边界框除了给出置信度的信息之外，还需要预测出检测框的中心坐标(x,y),检测框的宽度和高度(w,h)。检测框的中心坐标是相对于其所在小方格的偏移量，并以小方格的边长为基准归一化到[0,1]之间；而检测框的宽度和高度则是以输入图像的宽度和高度归一化到[0,1]之间。除了以上5个参数，对于每个边界框，还需要预测80个类别的概率。每个边界框预测的类别置信度可以由以下公式表示：

(3)

可以看出，最终预测的物体的置信度由方格内边界框的置信度乘以该方格预测出来的每个类别物体的条件概率得到。既反映了检测框包含某种待检测物体的概率，也反映了检测框定位该物体的效果。

Tiny-YOLOV3模型进行目标预测的具体过程包括以下4个阶段：首先对标注的真实边界框进行K-Means聚类[17]，自动提取具有代表性的锚框(anchor box)，与标注框交并比(IOU)最大的锚框作为训练时锚框的标签;之后对训练时输入的图像数据进行尺度缩放，即大小为416×416的图像数据;接着对输入数据进行卷积神经网络[18]的前向传播过程，生成2个不同尺度大小的特征图，针对每个特征图求取不同类别的概率以及检测框的位置，根据一个概率值来筛选概率低于阈值的检测框;最后根据非极大值抑制(NMS)算法筛选出多余的检测框，得到最终的物体检测框及置信度得分。

非极大值抑制算法就是一种逐步迭代获取局部极大值的一种方法，在目标检测中主要是为了消除多余的预测框，得到待检测目标的最佳位置。它的主要思想是：在图像上首先对所有的预测框的置信度进行排名，选取置信度最高的预测框作为基准；然后计算剩余预测框与基准预测框之间的交并比，如果大于设定的阈值，就删除该边界框；再从剩下的边界框中选取置信度最高的作为基准，重复以上过程，最终得到满足标准的最佳预测框。

1.2 Tiny-YOLOV3网络结构

Tiny-YOlOV3网络是YOLOV3网络的简化版本，网络结构如图1所示。与YOLOV3类似，网络中使用3×3和1×1两种大小的卷积核，3×3的卷积核主要用来提取图片的特征信息，1×1的卷积核可以在保持特征图尺寸不变的前提下增加非线性特征，减少网络训练的参数。卷积层包含卷积操作、批归一化处理和Leaky Relu三种基本操作。卷积操作是为了提取图片的特征；批归一化处理是通过一定的规范化方法，提高网络的训练速度，使网络的收敛过程大大加快，防止网络出现过拟合；Leaky Relu则是网络使用的非线性激活函数。Tiny-YOLOV3主干网络主要有7个3×3的卷积层及6个最大池化层，前5个最大池化层的步长为2，最后一个步长为1。当输入大小为416×416的图像时，整体网络的输出为13×13的特征图，经过上采样之后与第5个卷积层的输出进行张量拼接，再进行卷积运算得到26×26大小的特征图，最终网络输出两个不同尺度的特征图。小尺度特征图具有较大的感受野，适合检测大目标物体；大尺度特征图具有较小的感受野，适合检测小目标物体。

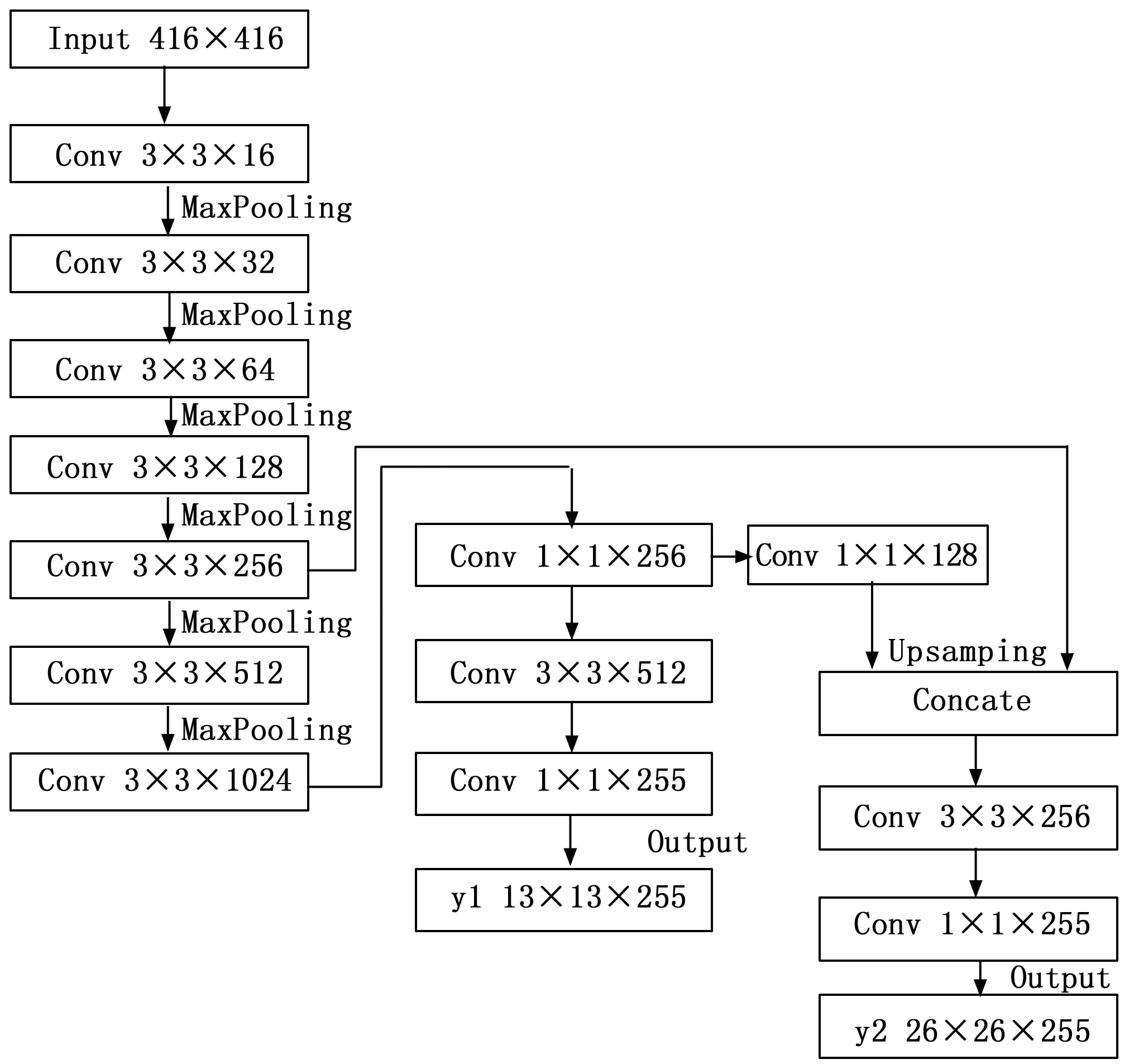
图1 Tiny-YOLOV3网络结构

相比较YOLOV3网络，Tiny-YOlOV3网络结构更加简单，网络层数大大减少，需要训练的参数大大减少，特别适合于工程实现。尤其在旋翼无人机进行目标跟踪时，由于机载处理器算力不足，无法运行深层的卷积神经网络模型，而针对无人机的目标跟踪又需要兼顾准确率和实时性的要求，那么Tiny-YOlOV3网络便成了首要选择。

2 四旋翼目标跟踪模型

由于Tiny-YOLOV3目标检测算法最终输出的是目标物体在像素坐标系下的像素坐标，因此要想计算目标在导航坐标系下的具体位置，需要先建立一个目标图像的跟踪模型，建立的模型如图2所示。

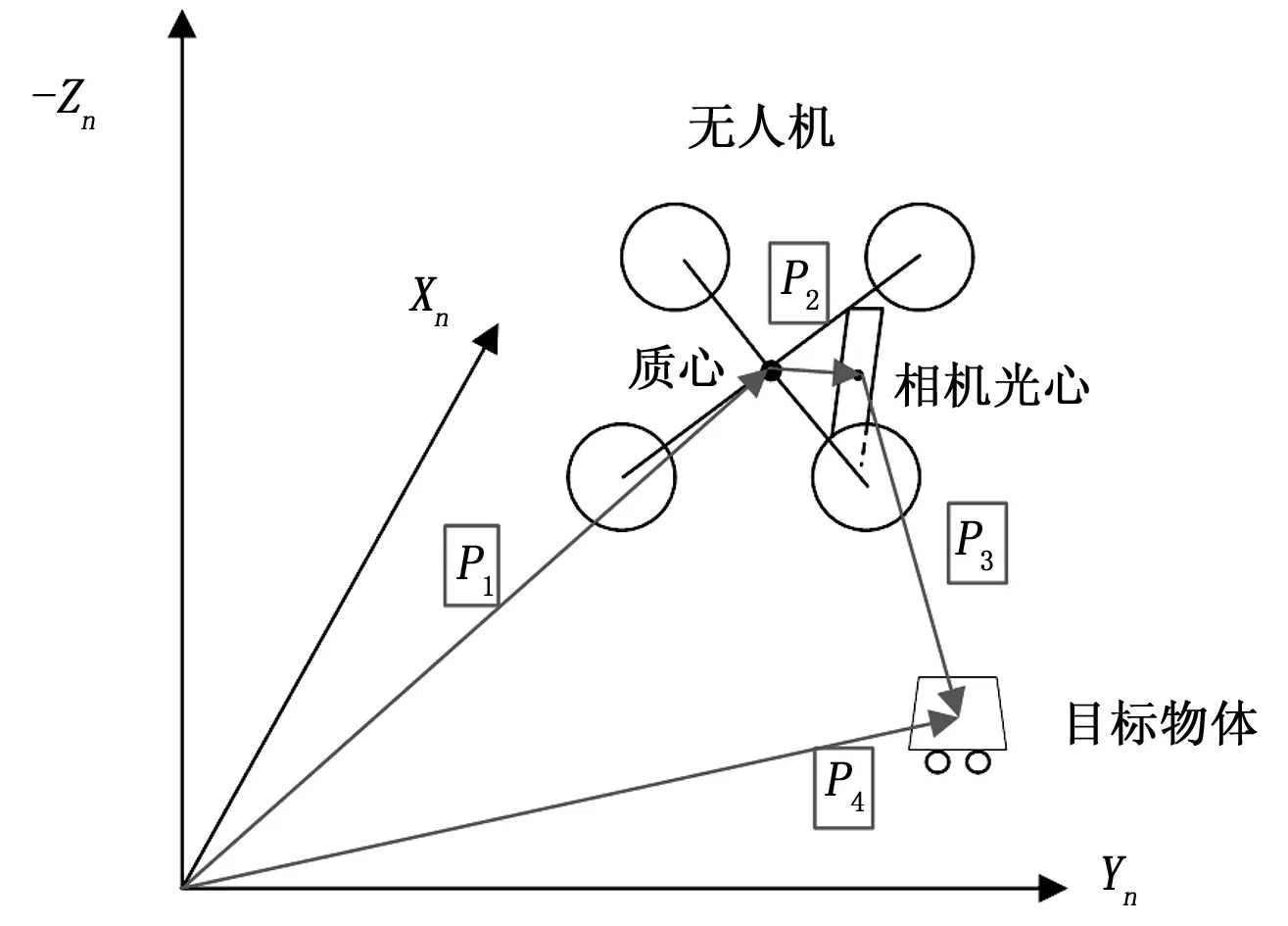
图2 四旋翼目标跟踪模型

根据几何关系，可以将目标位置P4=[xcn,ycn,zcn]由以下关系式表示：

P4=P1+P2+P3

(4)

P2=CbnbP2

(5)

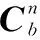
P3=CbnCcbcP3

(6)

P4=P1+CbnbP2+CbnCcbcP3

(7)

最终可以得出：

(8)

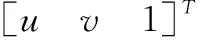
假设实际中目标所处位置处地形变化不大，因此可以确定地面的海拔高度为目标的位置zcn，令CbnCcbM1-1=C，则以下关系式成立，即:

(9)

从而图像深度信息计算如下：

(10)

最终计算出目标在导航坐标系下的位置为：

(11)

3 基于卡尔曼滤波的目标轨迹预测

由于机载处理器目标检测和识别的速度大概在13～14 FPS，也就是目标位置的更新频率在13～14 Hz ，而在无人机控制中，位置环的控制频率为20 Hz，同时考虑到目标检测算法有时会检测不到目标物体，导致目标跟踪效果较差。此外，考虑到检测结果的信号传输可能会受到设备本身和外界的干扰，因此需要建立目标的运动学模型，使用卡尔曼滤波器对目标位置进行滤波的同时预测目标物体的运动轨迹，保证目标位置更新频率与位置控制器更新频率一致，以实现四旋翼无人机对目标的稳定跟踪。

卡尔曼滤波器作为一种顺序最小二乘逼近，可以利用目标的动态信息，通过递推方法得到目标的最优估计。这个估计可以是对当前的估计，也可以是对过去的估计。对于卡尔曼滤波来说，只需要获得上一时刻的状态估计值以及当前时刻的量测信息就可以对当前时刻的估计值进行计算，因此它是一种递归估计。卡尔曼滤波器分为两个过程：时间更新和量测更新。时间更新是状态的预估过程，即通过一步预测方程建立对当前状态的先验估计，同时计算状态误差协方差估计值，以便为状态估计方程的计算做准备;量测更新即状态的校正过程，利用量测更新方程在时间更新过程中的先验估计值及当前量测值的基础上计算当前状态的后验估计。

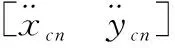
(12)

式中，Δt为更新周期。

(13)

式中，v(t)为量测噪声，可以考虑为高斯噪声。

对上面的运动学方程离散化可得状态转移矩阵、过程噪声成型矩阵和量测矩阵为：

(14)

式中，I为4×4的单位矩阵，Ts为相邻两帧图像之间的采样间隔，即目标检测算法识别目标的时间。

基于目标运动方程建立卡尔曼滤波方程，选取状态初值xcn0=ycn0=0，Vx0=Vy0=0.8 m/s，加速度噪声方差强度为Qax=Qay=0.000 9 m2/s4，量测噪声方差强度为Rvx=Rvy=0.001 6 m2。仿真结果如图3和图4所示。

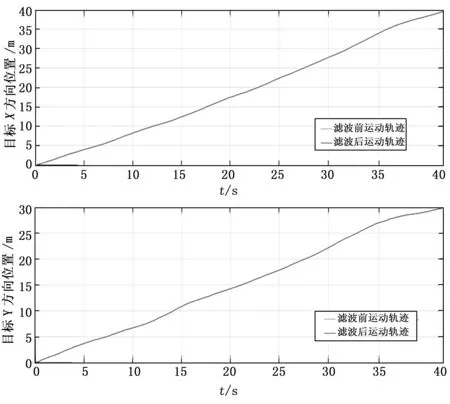
图3 滤波前后目标位置对比

图4 滤波误差

从仿真结果可以看出，采用卡尔曼滤波后，目标在x方向误差最大不超过0.06 m，在y方向误差最大不超过0.06 m，滤波前后运动轨迹基本一致，说明采用卡尔曼滤波对目标轨迹的预测效果很好。

4 四旋翼无人机控制律设计

对于四旋翼无人机来说，良好的控制律设计是无人机实现稳定飞行的前提。对四旋翼无人机来说，高度控制独立于姿态控制，位置控制则是基于无人机姿态的改变来进行控制的。因此为了保证无人机在目标跟踪过程中的稳定飞行，本节通过对实验室四旋翼无人机建立模型，分析设计后采用PID控制的方式，得到四旋翼无人机的控制律如下：

1)姿态控制律：

(15)

2)高度控制律：

(16)

式中，UT为高度控制量，m为旋翼无人机总质量，hg为无人机期望高度，h为无人机当前高度。

3)水平位置控制律：

(17)

其中：xg和yg为无人机水平期望位置，vxg和vyg为无人机水平期望速度，x和y是无人机当前水平位置，vx和vy为无人机当前水平速度，ux和uy是水平方向上等效控制量。

由于水平位置控制的最终目的是俯仰角和滚转角的控制，因此姿态控制器目标姿态角的输入为：

(18)

式中，φd和θd为姿态控制器滚转角和俯仰角的期望输入量。

5 仿真结果与分析

基于第4节设计的控制器，通过Matlab/Simulink搭建仿真模型，将经过卡尔曼滤波后的目标运动轨迹输入到位置控制器中，将目标的运动方向角作为四旋翼无人机偏航角的期望输入，得到最终的仿真结果。

5.1 四旋翼位置控制仿真结果

图5和图6为40 s内目标运动轨迹和四旋翼无人机运动轨迹，可以看出由于位置控制器存在调节时间，无人机运动相较于目标的运动存在一定的滞后，稳态误差维持在0.5 m以内，基本不影响跟踪的结果。最终目标水平位置为(39.56 m,29.88 m),无人机水平位置为(39.18 m,29.64 m),整体上两者运动轨迹基本一致。图7为三维空间下两者运动轨迹对比，无人机先飞行到6 m的高度，然后进行目标轨迹的跟踪，仿真结果表明虽然无人机与目标之间的运动轨迹存在一定的偏差，但不影响最终的跟踪效果。

图5 无人机位置控制结果

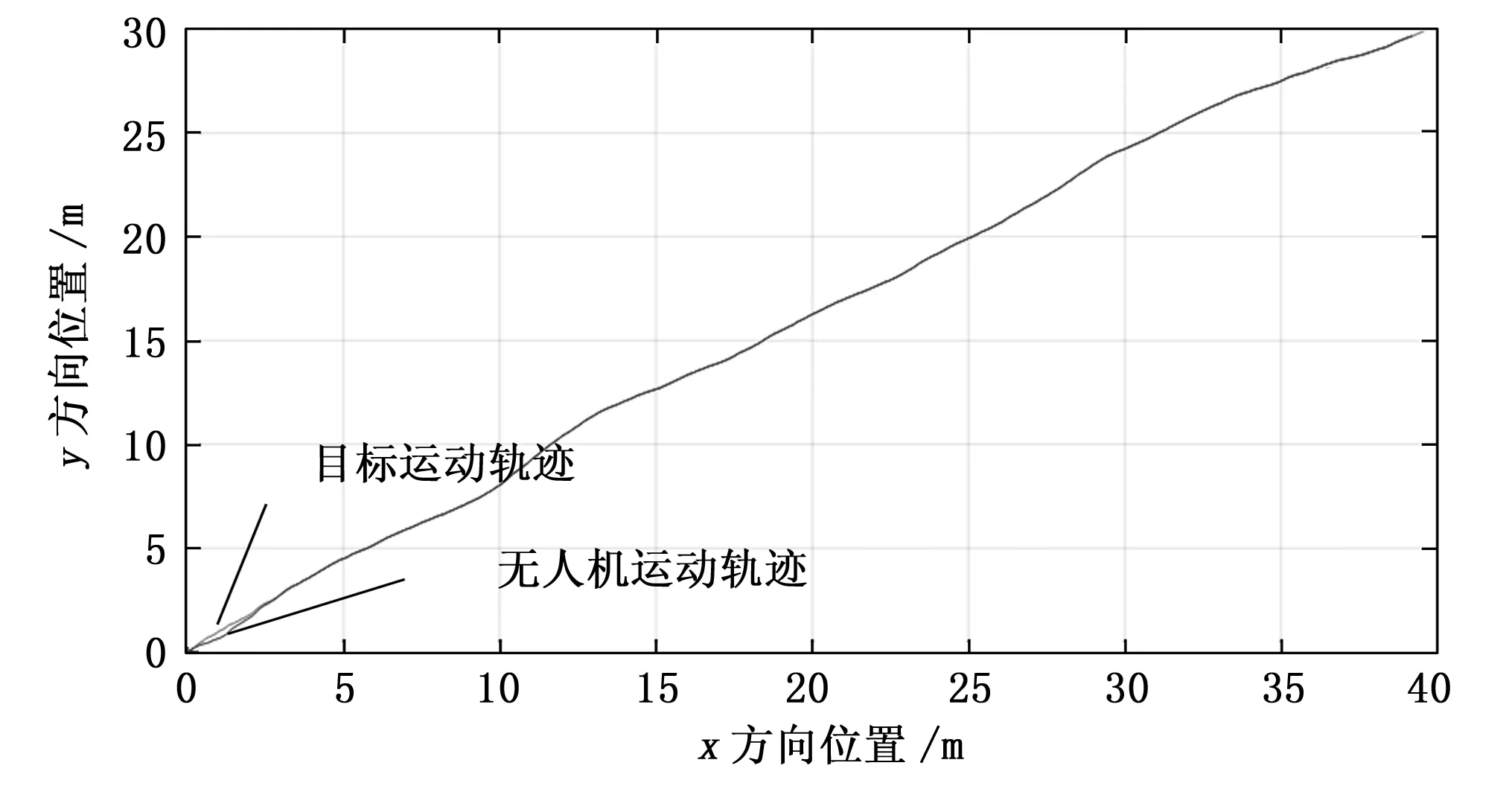
图6 二维空间下运动轨迹对比

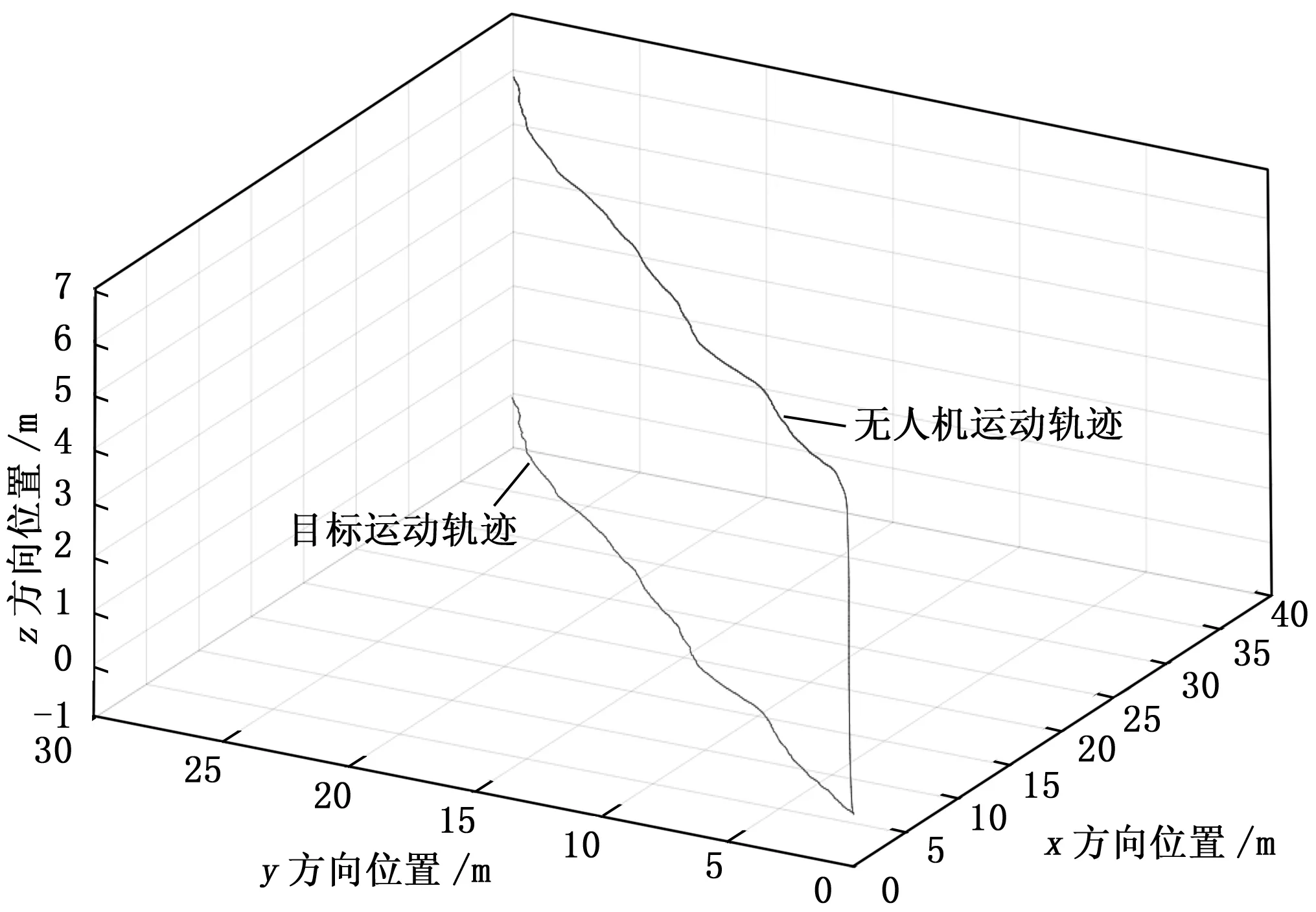
图7 三维空间下运动轨迹对比

5.2 四旋翼速度控制结果

图8为旋翼无人机的速度与目标运动的速度对比，初始时刻由于噪声的影响，目标速度存在跳变，无人机速度经过一定的调节时间慢慢跟踪上目标运动速度，虽然无人机速度有些滞后于目标速度，但整体偏差不超过0.2 m/s,速度运动曲线基本一致，说明旋翼无人机能够很好地保持与目标之间的相对静止。

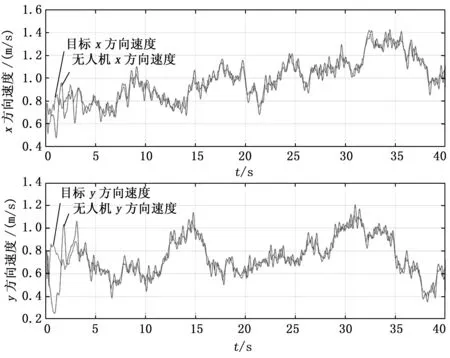
图8 运动速度对比

5.3 四旋翼航向控制结果

图9为目标与无人机运动方向对比，初始时刻由于噪声的影响，目标方向产生了突变，导致无人机与目标存在10°左右的夹角，经过一定的调节时间，无人机与目标的运动方向基本一致，稳态偏差在3°以内，航向控制效果良好。

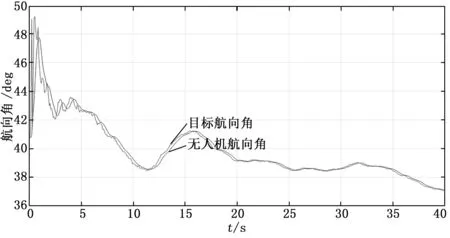
图9 运动方向对比

综上所述，四旋翼无人机跟踪地面目标的过程中，在轨迹跟踪的同时控制无人机的速度和方向，使无人机始终沿着目标的运动轨迹飞行。仿真结果表明无人机位置跟踪的精度在0.5 m以内，跟踪过程中与目标的速度偏差不超过0.2 m/s，同时在航向控制上基本与目标运动方向一致，跟踪效果良好。

6 结束语

本文针对Tiny-YOLOV3目标检测算法存在目标漏检的问题，同时考虑到实际中的噪声干扰和无人机控制器的更新频率，提出了一种联合Tiny-YOLOV3和KF的四旋翼无人机目标跟踪算法。通过建立目标跟踪模型并设计四旋翼无人机控制律，最终通过仿真验证了所提出算法的稳定可靠性。所提出的算法可以实现对单一目标的稳定跟踪，但针对多个同类目标，还需对算法进行深入研究。