常用H型钢次梁端部节点力学性能研究

吴贤明

(中铁第四勘察设计院集团有限公司 湖北武汉 430063)

1 国内外研究现状

国内外对于半刚性接连节点问题的研究，目前主要是在梁柱节点上。国内的研究基本集中在H型钢柱-H型钢梁连接节点，方钢管柱-H型钢梁连接节点这两种主要的半刚性梁 柱节点的静、动力性能方面，对于其它梁柱连接形式的节点几乎没有涉及，主次梁之间连接节点的研究尚未见报道；而在钢结构设计中，连接主梁与次梁，同时起着传递弯矩和剪力作用的梁端节点[1]，是钢结构框架的主要组成部分。国内比较有代表性的研究为楼国彪的高强度螺栓端板连接的研究现状和进展，同时还对节点的承载力计算与相关设计方法进行了简化处理。同时，他也进行了相关的有限元分析，构建了弯矩-转角曲线的数学表达模型，总结了端板连接抗火性能研究的现状[2-3]； 此外，李黎明提出了一种新的节点连接方式，称为外套管式梁柱节点连接[4-6]，参照EC3中的相关内容，提出了运用组件法来计算此种连接节点的初始刚度。

国外的研究工作开始较早，其中有代表性的成果为1976年，Frye和Morris通过建立多项式模型，成功地计算了几种连接节点的相关力学特性[7]；1982年，Jones等人采用样条曲线对连接节点的弯矩-转角(M·θ)曲线关系作了拟合，但需要很大的计算数据量来作为支持，而且拟合过程相当繁琐[8]；1983年，Colson和Louveau首次提出了幂函数模型，该模型的建立基于3个相关参数[9]；随后，Kishi和Chen对Colson和Louveau提出的幂函数模型做了一定的改进工作，提出了一种和幂函数模型相似的计算模型，大大减少了计算所需的数据量[10]。1986年，Lui和Chen提出了一个指数模型，该模型由多个参数所组成，为弯矩-转角曲线的进一步拟合创造了新的途径[11]。

虽然各个国家的科研工作者和学者均做了大量有关半刚性连接节点的实验工作，但由于实验数据的自身不足性，则需要通过运用必要的理论分析来进行补充和完善。目前通常的做法是，对特殊类型的节点采用有限元软件进行建模和计算分析。

2 有限元模型验证

2.1 试验验证

文献[12]进行了腹板栓接主次梁节点的试验研究，主次梁构件截面尺寸如表1所示，其试验过程、节点构造及螺栓的设置等相关情况如图1～图2所示。为了验证本文的建立有限元模型方法的可靠性与准确性，将对比和分析有限元软件的计算结果与文献[12]的试验结果。

表1 主次梁构件截面尺寸 mm

图1 试验节点构造细部图

图2 试验节点构造侧面图

2.2 ANSYS有限元模型的建立及分析结果

(1)考虑本研究的腹板栓接主次梁半刚性节点的结构特性，以及所施加荷载的对称性特征，本研究采用1/2的有限元模型来对整个主次梁节点和相连的次梁结构进行模拟和计算分析；同时，按照实际工程情况设置模型的约束条件。

(2)考虑结构自身是由纯钢节点组成，因此，其中的梁、连接板及螺栓等钢构件均采用SOLID185单元进行模拟；采用螺栓杆侧壁与螺栓孔之间的接触，对采用TARGE170 和CONTA174单元进行模拟。

(3)由于本研究对象的有限元几何模型建立方式是“体”生成，因此选择“体扫略”来对其进行网格划分。“体扫略”不仅能够自行控制网格划分时的粗细程度，而且每个计算单元相对容易收敛，计算效率较高。

(4)有限元模型中所选取的单元及其相应的特性参数，主次梁构件的尺寸和材料参数均按照上述具体试验数据确定。建立的符合真实受力状态的主次梁连接节点模型如图3～图4所示。利用ANSYS有限元分析软件的后处理功能提取有关数据，分别计算整个分析过程中的弯矩值和转角，该弯矩-转角关系曲线，如图5所示。

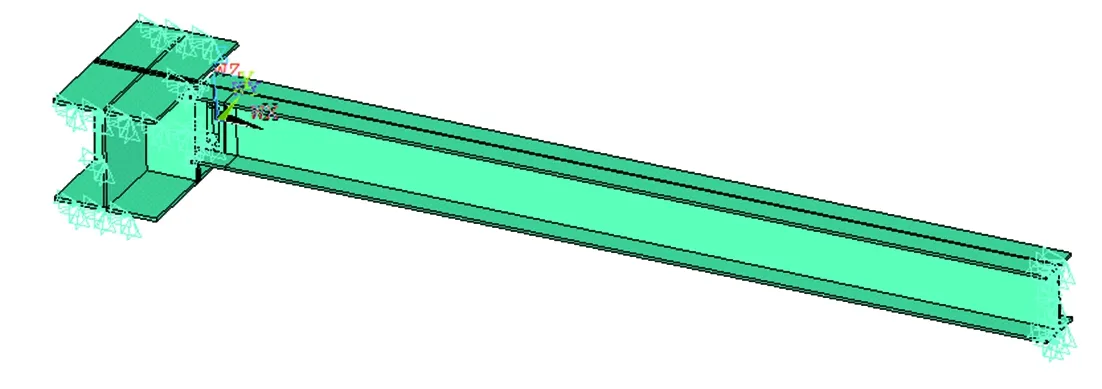
图3 模型整体图

图4 节点细部图

2.3 ANSYS有限元计算结果与试验结果对比

将ANSYS有限元计算分析得到的弯矩-转角关系曲线同试验统计作出弯矩-转角关系曲线进行对比，如图6所示。

图5 节点的(M·θ) 曲线图

图6 有限元分析结果与试验结果对比图

由图6可以看出，有限元计算和分析结果与试验作出的统计结果吻合较好。

综上，本研究所建立的有限元模型方法，能够较好地模拟腹板栓接主次梁节点的工作性能，其计算结果可靠。

3 工程中典型次梁不同截面力学性能分析

主梁截面采用500×200×8×10mm，次梁截面采用200×100×3×3mm，具体尺寸如表2所示，相应的建模及计算结果如图7～图8所示。

表2 主次梁构件截面尺寸 mm

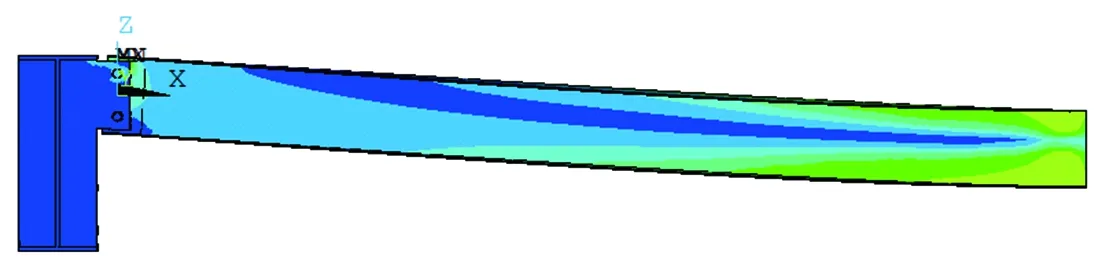
图7 整体模型变形正面图

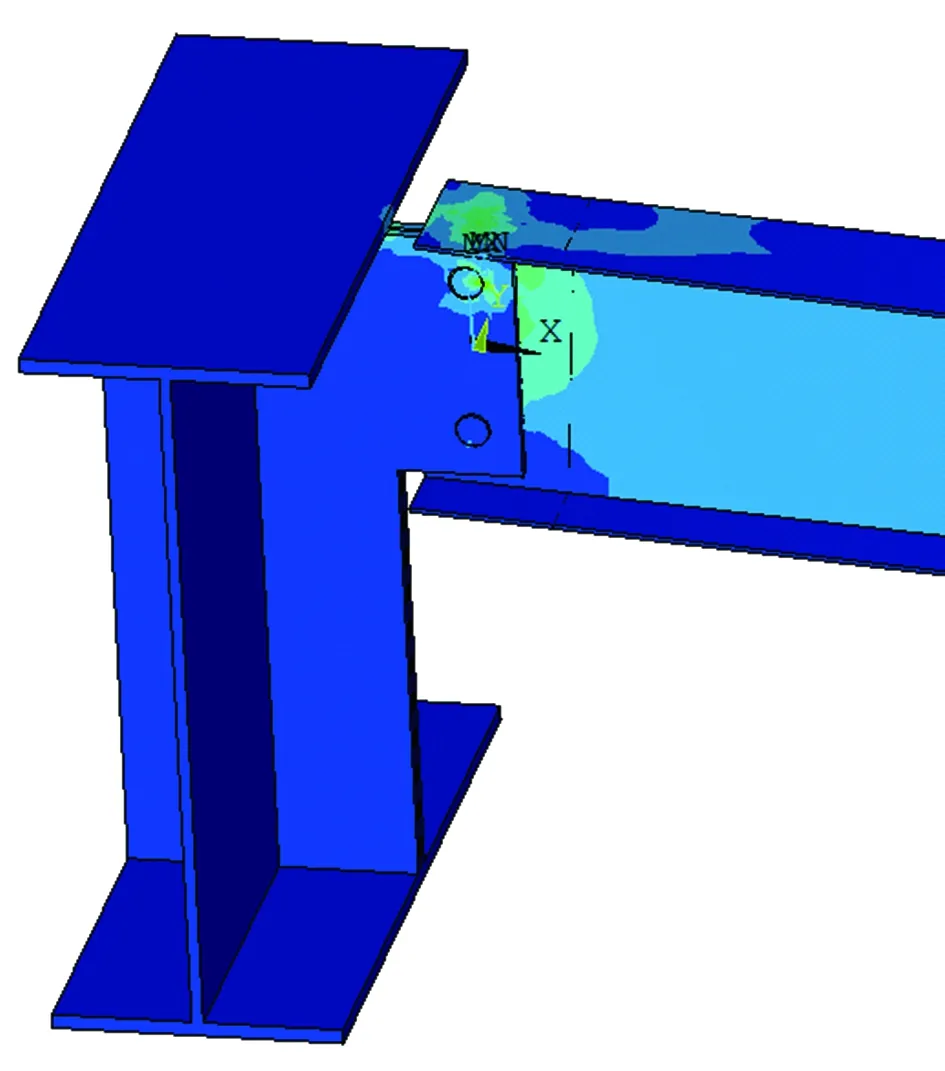
图8 节点细部变形图

选取其中典型的荷载子步进行分析，ANSYS有限元分析计算结果如表3所示。

表3 相对转角-弯矩值计算表

图9 200×100×3×3mm节点M-θ曲线图

本研究绘制其(M·θ)曲线如图9所示，横坐标代表螺栓部分的相对转角θ(°)，纵坐标代表节点连接部分所承担的弯矩值M(kN·m)。

节点转动刚度(割线刚度)统计表如表4所示。

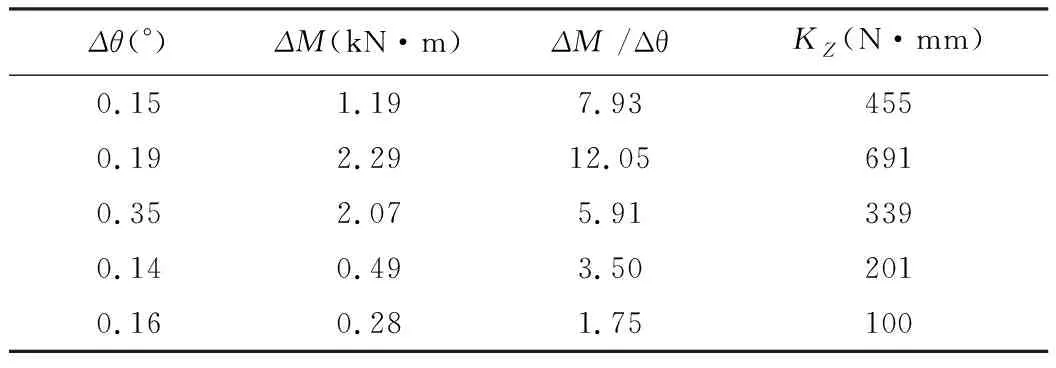
表4 节点转动刚度统计表

节点弯矩值及传递百分比统计表如表5所示。

表5 节点弯矩传递值及百分比统计表

H型截面次梁200×100×3×3mm的线刚度i=EI/l，其值为定值314 N·mm，线刚度的一半i/2为157 N·mm。由表5可知，此时节点的初始转动刚度Kz，稳定时其值为450 N·mm左右，弯矩传递百分比最终维持在9.71%。

同理，不改变主梁截面尺寸，次梁截面分别取为200×150×6.0×8.0mm、300×150×4.5×6.0mm、350×100×6.0×8.0mm、400×150×4.5×8.0mm、400×200×6.0×8.0mm、400×200×7.0×11.0mm。将得出的各自弯矩传递百分比绘出的M-θ曲线对比如图10所示。

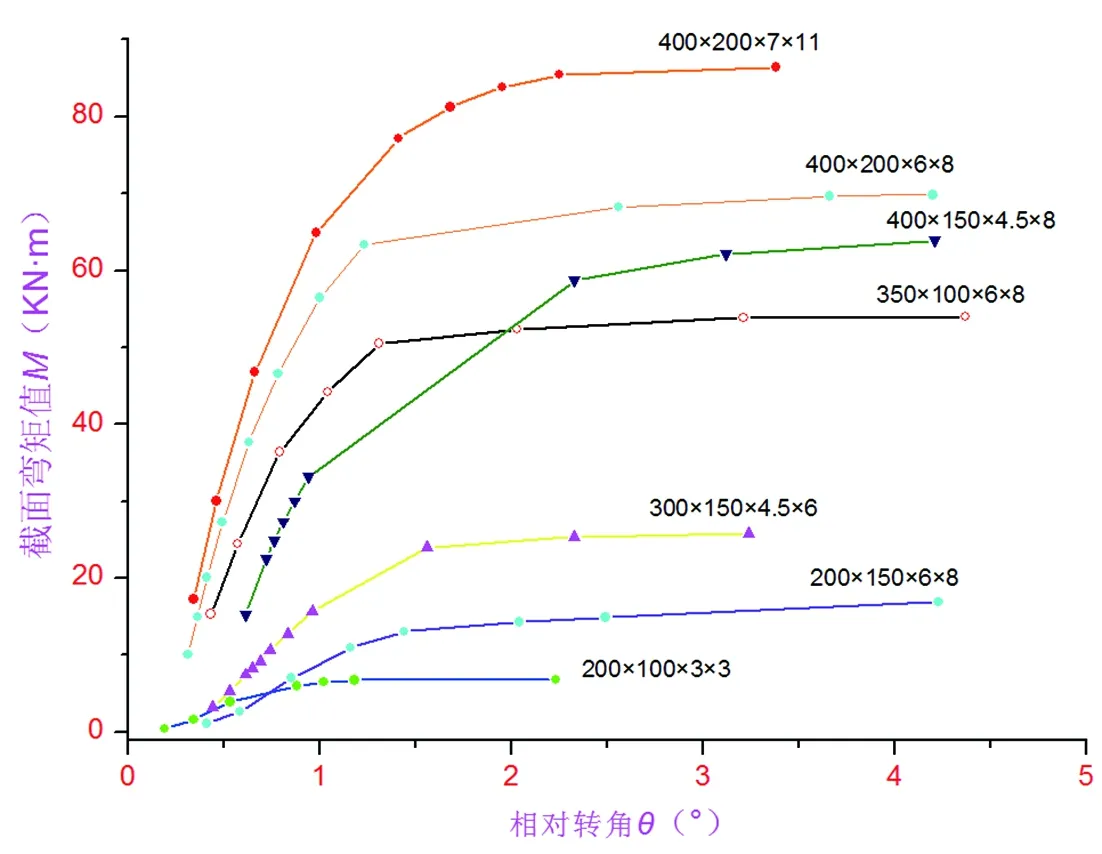
图10 常用截面形式节点的M-θ曲线对比图

4 结论

从上述几种常用H型截面次梁的计算和分析，并结合图10(M·θ曲线对比图)可知：

(1)常用腹板栓接主次梁连接节点自身的转动刚度，并不是固定不变的。 节点初始转动刚度与次梁线刚度之间的相对大小，会导致节点连接部分最终分担的弯矩有所不同。

(2)当主次梁节点的转动刚度比次梁线刚度小很多时，该连接节点仍可按理想铰接考虑。但是，如果两者的刚度差距不是特别明显，则必须严格考虑腹板栓接主次梁节点的半刚性特征。

(3)通过比较可以发现，常用腹板栓接半刚性连接的节点部分，其所传递的弯矩百分比值基本稳定在10%左右。此结论为设计单位提供了相当有价值的参考，即在进行此类半刚性节点设计时，很有必要考虑这10%弯矩传递比。这样设计出来的腹板栓接主次梁节点不仅安全合理，而且经济适用。