自旋轨道耦合串联双量子点系统的电流有限频率噪声谱

马骁燕，段志磊，薛海斌*

（1.太原理工大学 新材料界面科学与工程教育部重点实验室，山西 太原 030024；2.太原理工大学 物理与光电工程学院，山西 太原 030024）

0 引言

量子点因其能级的分立性和高度可调性，被称为“人造原子”。其中，耦合双量子点由于其每个量子点能级都可以通过门电压独立地调节和其固有的量子相干性，因而，成为研究各种量子力学效应和开发相关量子技术的理想系统和研究平台［1—5］。在基于耦合双量子点的自旋量子器件中，其电子自旋自由度的有效操控是至关重要的［6—9］。由于操控自旋的磁场在小尺度空间内难以聚焦，因此，基于可以在小尺度空间内聚焦的电场，即，通过电场可调的自旋轨道耦合效应操控电子自旋成为凝聚态物理的热点研究领域之一［10］。对于不同结构和不同材料构建的耦合双量子点，有效自旋轨道耦合场的大小通常不同，而准确获取其大小将有助于深入分析和全面理解电子自旋自由度的操控。因而，探测耦合双量子点内有效自旋轨道耦合场的大小引起人们的研究兴趣［11—12］。例如，在存在各向异性交换相互作用的双量子点中，有效磁场的不均匀性可以反映其自旋轨道耦合强度［11］；在InSb双量子点中，单态—三重态能级排斥的大小和其各向异性可以用来确定有效自旋轨道耦合场的大小和方向［12］。但是，如何基于耦合双量子点的量子输运特性定量提取其有效自旋轨道耦合场的大小仍然是一个开放的课题。

另外，对于纳米尺度的耦合双量子点，瞬时电流涨落将非常明显，此特性可以用其电流有限频率噪声谱描述。尤其是，有限频率噪声谱可以提供更多平均电流（微分电导）和零频散粒噪声无法获取的信息［13—26］。例如，与耦合双量子点内部能量结构相关的输运时间尺度［13—23］以及其内禀动力学特性［14—26］的信息。对于串联耦合双量子点体系，当电子在两个量子点之间仅有自旋守恒的跳跃隧穿过程时，电流有限频率噪声谱上谷的位置等于其2个相干单占据本征态能量本征值之差相应的频率［23］。但是，对于存在自旋轨道耦合效应的情形，电子在两个量子点之间不仅有自旋守恒的跳跃隧穿过程，而且有自旋翻转的跳跃隧穿过程。此时，串联耦合双量子点有4个相干单占据本征态，是否所有相干单占据本征态的能量本征值之差都对应一个相干振荡频率？是否电流有限频率噪声谱在每一个相干振荡频率处一定出现谷？若电流有限频率噪声谱在相干振荡频率处出现峰，则峰、谷形成的物理机制是什么？这些问题都需要进一步研究。尤其是，如何基于电流有限频率噪声谱定量提取自旋轨道耦合场的大小尚未被揭示。

本文将研究电子通过自旋轨道耦合串联双量子点的电流有限频率噪声谱，重点分析电流有限频率噪声谱中峰、谷的位置、存在条件，以及其形成的物理机制，并讨论基于峰、谷的位置定量提取有效自旋轨道耦合场大小的理论方案。研究发现，串联耦合双量子点的量子相干性是电流有限频率噪声谱中峰和谷存在的本质原因；而其4个相干单占据本征态的能量本征值之差决定了峰、谷的位置。其中，该能量本征值之差的简并度为2和1分别对应于谷和峰。因而，基于电流有限频率噪声谱在不同外加磁场下的峰、谷位置，可以定量获取量子点之间自旋守恒的电子跳跃隧穿强度和自旋轨道耦合场参数的大小。这些结果为通过自旋轨道耦合效应有效操控串联耦合双量子点的电子自旋自由度提供了一定的理论基础。

1 模型与方法

1.1 与铁磁电极耦合的自旋轨道耦合串联双量子点

考虑自旋轨道耦合串联双量子点与两个铁磁电极弱耦合的系统，如图1所示，其哈密顿量可表示为：

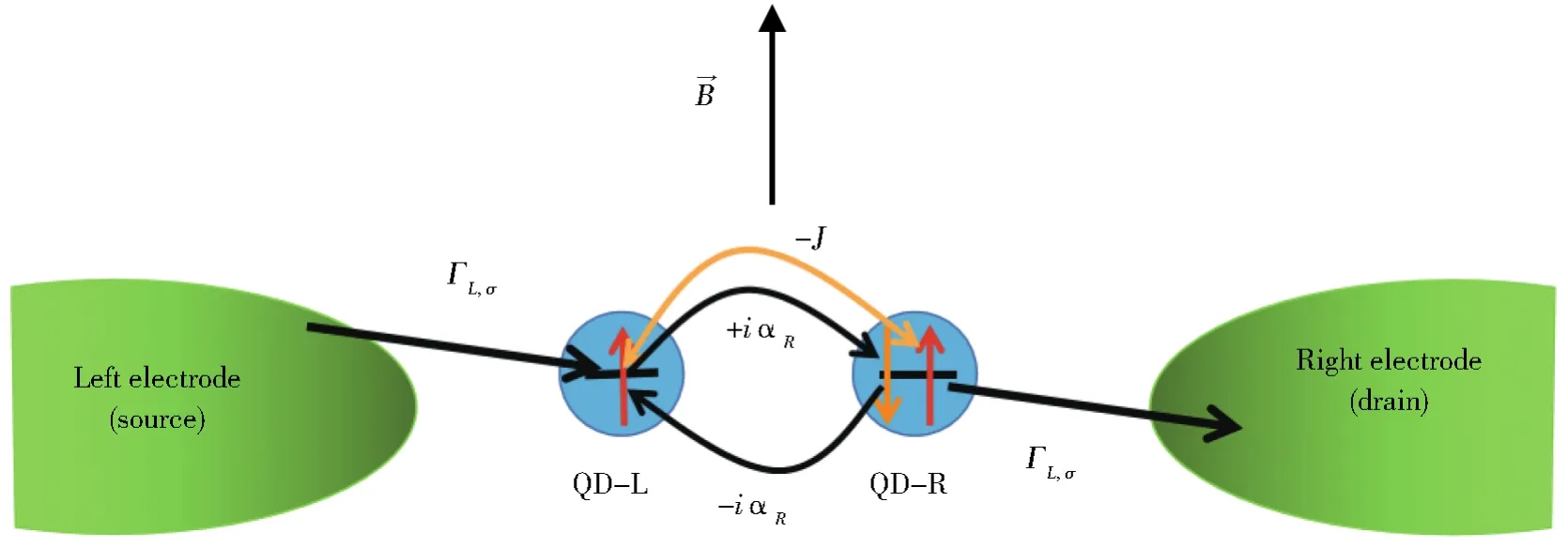
图1 自旋轨道耦合串联耦合双量子点与左、右铁磁电极弱耦合的示意图。其中，左、右量子点之间电子自旋守恒和自旋翻转的跳跃隧穿分别用-J和αR表示。例如，对于自旋为σ的传导电子，其从左量子点到右量子点的电子自旋翻转跳跃隧穿用iαR表示，反之，传导电子从右量子点到左量子点的自旋翻转电子跳跃隧穿用-iαR表示。此外，量子点与α电极之间自旋依赖的隧穿耦合强度用 Гα，σ表示Fig.1 The serially coupled double-quantum-dot（DQD）system with Rashba spin-orbit coupling weakly coupled to two electrodes.Here，the spin-conserving hopping and spin-flip hopping from the QD-L to the QD-R are characterized by-J and αR，respectively.For example，iαRcharacterizes the spin-flip hopping from the QD-L to the QD-R，whereas-iαRcharacterizes that from the QD-R to the QD-L.Furthermore，Гα，σdenotes the spin-dependent tunneling strength between the QD-α and the electrode α

这里，（1）式右边第一项HQD-SOC表示自旋轨道耦合串联双量子点的哈密顿量［27—28］

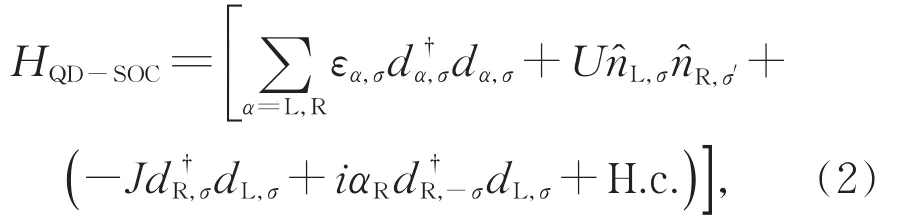
其中，εα，σ＝εα+σB/2和分别表示量子点α的电子能量和电子产生（湮灭）算符；这里，σ＝↑＝+，σ＝↓＝—，B是能级εα，σ的塞曼劈裂能。U表示两个量子点的点间库仑相互作用，J表示两个量子点之间电子自旋守恒的跳跃隧穿。由于串联耦合量子点存在自旋轨道耦合效应，因此，两个量子点之间还存在电子自旋翻转的跳跃隧穿，其强度用αR刻画。例如，传导电子从左量子点到右量子点的电子自旋翻转跳跃隧穿用iαR表示，反之，从右量子点到左量子点的电子自旋翻转跳跃隧穿用—iαR表示。为方便讨论，这里假设量子点内电子的库仑相互作用足够大，以至于在本文考虑的偏压区域内，每个量子点最多只能占据一个电子。

（1）式右边的第二项表示左、右电极的哈密顿量。若电极库中电子的弛豫过程足够快，此时，其电子分布可用平衡态费米分布函数表示，因而，其哈密顿量可表示为

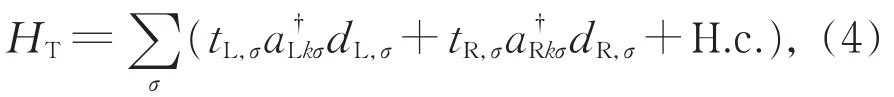
1.2 电流有限频率噪声谱

对于本文考虑的串联耦合双量子点与铁磁电极弱耦合的情形，电子的顺序隧穿过程在电子输运中占据主导地位。因此，电子通过串联耦合双量子点的隧穿过程可由其约化密度矩阵遵循的粒子数分辨量子主方程描述。在玻恩近似和马尔可夫近似下，系统的粒子数分辨量子主方程可以表示为：［18，29］

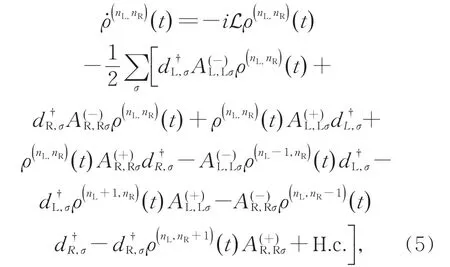
1.3 串联耦合双量子点系统的本征值和本征态

为方便讨论，假设偏置电压Vb对称地施加在量子点与铁磁电极构成的隧穿结上，即，μL＝—μR＝Vb/2，并且选择串联耦合双量子点最多仅占据一个传导电子的偏压区域。在此偏置电压区域内，由于传导电子的双占据被禁止，因而，传导电子隧穿进双量子点只能通过空占据到单占据本征态的转变实现，而隧穿出双量子点只能通过单占据本征态到空占据的转变实现。这里，选取串联耦合双量子点的本征态描述系统的电子状态变化。对于电子空占据的情形，其本征值和相应的本征态为

通过求解矩阵M的本征问题可得如下4个相干单占据本征态，

2 结果与讨论

在本部分，研究串联耦合双量子点自旋轨道耦合场参数αR对其电流有限频率噪声谱的影响；重点讨论电流有限频率噪声谱中峰和谷存在与形成的条件、如何确定峰和谷的位置、峰的高度或者谷的深度变化的物理机制；最后，探讨基于其有限频率噪声谱定量提取自旋轨道耦合场大小的理论方案。在下面讨论中，串联耦合双量子点的参数选取为U＝5.0，ε＝εL＝εR＝1.0，μL＝—μR＝Vb/2＝7，kBT＝0.04，其中，能量单位选取为毫电子伏特［31］（meV）。

2.1 自旋轨道耦合场大小对电流有限频率噪声谱的影响

对于不同自旋轨道耦合场的情形，由图2可知，电子通过串联耦合双量子点的电流有限频率噪声谱有两个峰和两个谷，并且峰、谷的位置，以及峰的高度和谷的深度均依赖于自旋轨道耦合场的大小。下面，分别讨论峰、谷存在与形成的条件，峰、谷位置的依赖因素，以及峰的高度或谷的深度变化的物理机制。

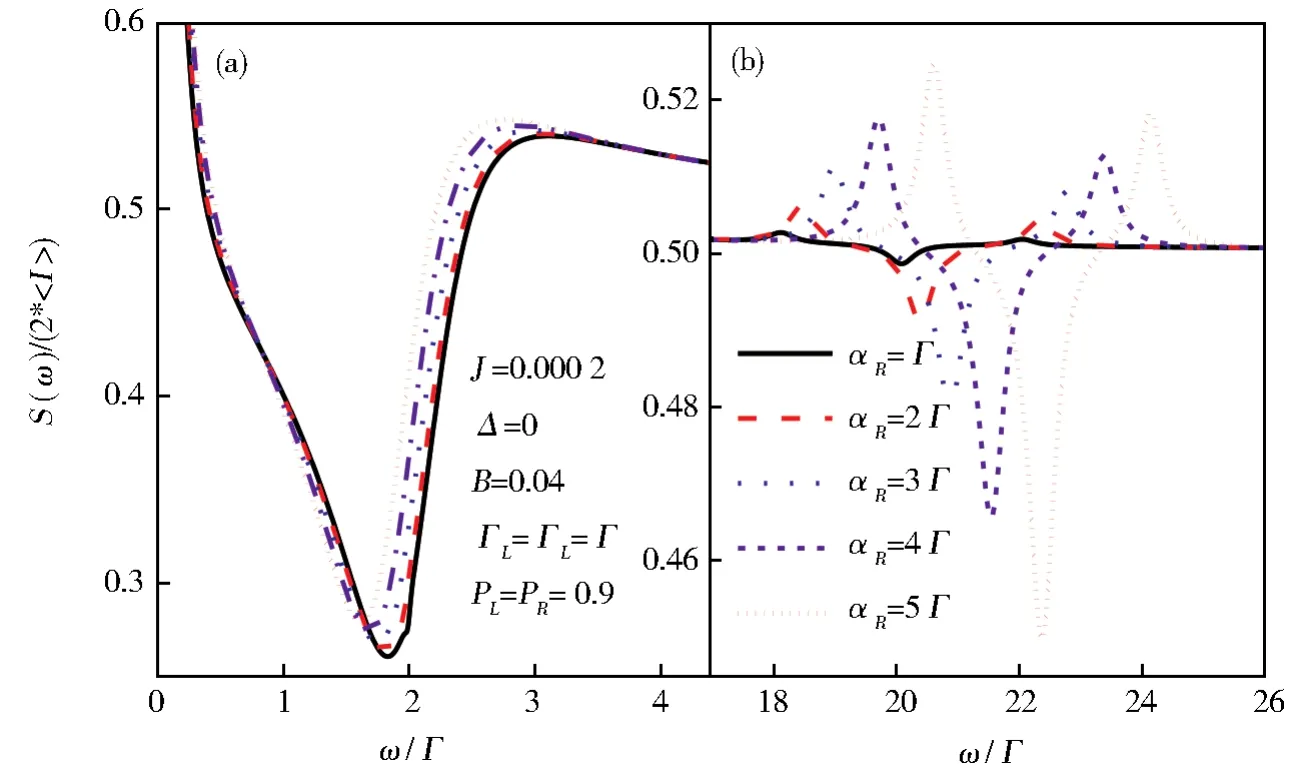
图2 电流有限频率噪声谱在不同自旋轨道耦合场情形下随频率ω的变化，（a）电流有限频率噪声谱的第一个谷，（b）电流有限频率噪声谱的第一个峰、第二个谷和第二个峰。其中，频率ω的单位选取为Γ。系统的参数选取为：U＝5.0，μL＝—μR＝Vb/2＝7，kBT＝0.04，pL＝pR＝p＝0.9，εL＝εR＝1.0，ΓL＝ΓR＝Γ＝0.002，J＝0.002，B＝0.04Fig.2 Fano factor of the finite-frequency shot noise as a function of the frequency for the different values of the SOC αR，（a）the first dip of the current finite-frequency shot noise，（b）the first peak，second dip and second peak of the current finite-frequency shot noise.Here，the unit of the frequency is chosen asΓ.The parameters of the system considered are taken asU＝5.0，μL＝—μR＝Vb/2＝7，kBT＝0.04，pL＝pR＝p＝0.9，εL＝εR＝1.0，ΓL＝ΓR＝Γ＝0.002，J＝0.002，B＝0.04

首先，讨论电流有限频率噪声谱中峰、谷存在的条件。对于具有自旋轨道耦合效应的串联耦合双量子点，其相干单占据态由四个本征态组成，而电流有限频率噪声谱与其系统的量子相干性相关。因而，这里需要考虑串联耦合双量子点的量子相干性对其有限频率噪声谱的影响。在密度矩阵理论中，串联耦合双量子点的量子相干性由其约化密度矩阵的非对角元刻画。为不失普遍性，对于任取的一组参数，图3给出了仅考虑约化密度矩阵对角元、考虑约化密度矩阵对角元和非对角元两种情形下，左电极、右电极、自旋轨道耦合双量子点以及整个系统的有限频率噪声谱。当考虑约化密度矩阵的对角元和非对角元时，即考虑串联耦合双量子点的量子相干性时，左、右电极、自旋轨道耦合双量子点的有限频率噪声谱在4个不同的频率位置展现出峰或者谷，如图 3（a）、3（b）和 3（c）中的虚线所示。而对于整个系统的有限频率噪声谱，则出现两个峰和两个谷，如3（d）中的虚线所示。相反，当不考虑串联耦合双量子点的量子相干性时，左、右电极、自旋轨道耦合双量子点的有限频率噪声谱均展现出平滑的曲线，如图 3（a）、3（b）和3（c）中的实线所示。相应地，整个系统的有限频率噪声谱则观察不到峰和谷，如3（d）中的实线所示。因此，串联耦合双量子点的量子相干性决定了其电流有限频率噪声谱中是否存在峰、谷。

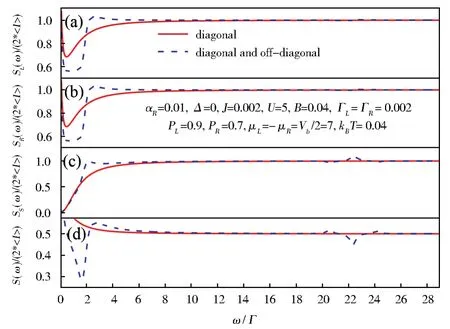
图3 量子相干性对（a）左电极、（b）右电极、（c）自旋轨道耦合双量子点以及（d）整个系统有限频率噪声谱的影响。其中，频率ω的单位选取为Γ，实线表示仅考虑约化密度矩阵对角元的情形；虚线表示考虑约化密度矩阵对角元和非对角元的情形。系统的参数选取为：αR＝0.01，εL＝εR＝1.0，J＝0.002，U＝5.0，B＝0.04，ΓL＝ΓR＝Γ＝0.002，pL＝0.9，pR＝0.7，μL＝—μR＝Vb/2＝7，kBT＝0.04Fig.3 Influences of quantum coherence on the finite-frequency shot noise，（a）the left electrode，（b）the right electrode，（c）the DQD with SOC，and（d）the total system.Here，the unit of the frequency is chosen asΓ.The solid lines denote the case of considering the diagonal elements of the reduced density matrix only，while the dashed lines denote the case of considering the diagonal and offdiagonal elements of the reduced density matrix.The parameters of the system considered are taken asαR＝0.01，εL＝εR＝1.0，J＝0.002，U＝5.0，B＝0.04，ΓL＝ΓR＝Γ＝0.002，pL＝0.9，pR＝0.7，μL＝—μR＝Vb/2＝7，kBT＝0.04

其次，讨论电流有限频率噪声谱中峰、谷的形成条件及其位置的依赖因素。对于串联耦合双量子点体系，当电子在两个量子点之间仅有自旋守恒的跳跃隧穿过程时，其电流有限频率噪声谱中谷的位置ωdip等于有效电子自旋守恒跳跃隧穿强度J的2倍［23］，即，ωdip＝2J。事实上，若利用串联耦合双量子点的本征态描述其电子状态变化，则电流有限频率噪声谱中的谷位置等于相干单占据本征态相应能量本征值之差［23］。对于两个量子点之间存在电子自旋翻转跳跃隧穿的情形，由（10）式可知，当串联耦合双量子点仅可被一个传导电子占据时，相干单占据态由四个本征态组成，可以形成12个非对角元，这里，i≠j；相应的能量本征值之差的绝对值|ε1，i—ε1，j|有如下4个：

在图4中，给出了12个非对角元相应的能量本征值之差|ε1，i—ε1，j|，即（19）式—（22）式描述的能量本征值之差随着自旋轨道耦合参数αR的变化。由图2和图4可知，若两组非对角元相应的能量本征值之差相等，例如，|ε1，1—ε1，2|与|ε1，3—ε1，4|，|ε1，1—ε1，3|与|ε1，2—ε1，4|，即，其能量本征值之差的简并度为2，其相应的频率位置ε+—ε—和ε++ε—对应于有限频率噪声谱中的谷；而对于单个的非对角元相应的能量本征值之差，例如，|ε1，2—ε1，3|和|ε1，1—ε1，4|，即，其能量本征值之差的简并度为1，则其相应的频率位置2ε—和2ε+对应于有限频率噪声谱中的峰。

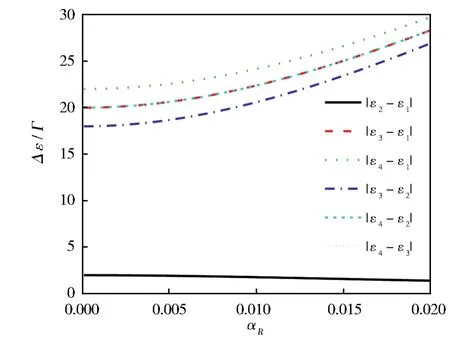
图4 两个相干单占据本征态能量本征值的差值随自旋轨道耦合参数αR的变化。其中，系统的其他参数与图2相同Fig.4 Eigenenergy differences of the coherent singly-occupied eigenstates as a function of the SOCαR.The other parameters are same to those for Fig.2

当自旋轨道耦合场参数αR增大时，非对角元相应的能量本征值之差ε+—ε—的数值将小幅度减小，如图4中的实线和短点线所示，相应地，第一个谷位置对应的频率将向低频方向移动，如图2（a）所示。但是，非对角元相应的能量本征值之差2ε—、ε++ε—、2ε+的数值随着自旋轨道耦合场参数αR的增大而明显增加，因而，相应的第二个谷和两个峰的位置将向高频方向移动，如图2（b）所示。因此，在串联耦合双量子点中，其电流有限频率噪声谱中峰和谷的位置依赖于非对角元相应的能量本征值之差，但是否形成峰或者谷依赖于非对角元相应的能量本征值之差的简并度。

最后，讨论电流有限频率噪声谱峰的高度或谷的深度变化的物理机制。对于最多只有一个传导电子占据串联耦合双量子点的偏压区域，一个自旋为σ的传导电子从源极隧穿到串联耦合双量子点后，由于两个量子点之间存在自旋守恒和自旋翻转的电子跳跃隧穿，将以一定概率形成4个相干单占据本征态，即，，因而，在该传导电子通过输运通道隧穿出串联耦合双量子点到达漏极之前，将在任意两个相干单占据本征态之间作相干振荡。对于本文考虑的偏压区域，串联耦合双量子点最多可占据一个传导电子，因而，传导电子在相干单占据本征态之间的相干振荡将会阻止其他传导电子从源极隧穿进串联耦合双量子点。此时，依赖于时间的涨落电流将在相干振荡频率处ω＝|ε1，i—ε1，j|偏离其平均值，从而在电流有限频率噪声谱中展示出峰或谷。

对于相干单占据本征态，由（10）式可知，每个单占据本征态都由四个电子态叠加形成，其中，单占据本征态塌缩到电子态的概率决定了传导电子通过输运通道隧穿出右量子点到达漏极的快慢，进而影响电流有限频率噪声谱中峰的高度或者谷的深度。下面以第二个谷为例进行解释。由图4可知，第二个谷由传导电子在相干单占据本征态之间，以及之间的相干振荡形成。对于单占据本征态，其塌缩到电子态的概率远大于，如图5中的实线、虚线、点线和点划线所示。虽然电子态的概率随着自旋轨道耦合场参数αR的增大会小幅减小，但是，对于电极极化率为pL＝pR＝p＝0.9的情形，相应的电子态中自旋向下的电子相对更难以隧穿出串联耦合双量子点到达漏极，因而，电子态概率的微小变化基本不影响传导电子在相干单占据本征态之间的相干振荡。随着自旋轨道耦合场参数αR的增大，单占据本征态塌缩到电子态的概率将减小，如图5中的双点划线和短点线所示，而塌缩到电子态的概率将增大，如图5中的短虚线和短点划线所示。相应地，传导电子更难隧穿出串联耦合双量子点到达漏极。因此，传导电子在相干单占据本征态之间的相干振荡将随着自旋轨道耦合场参数αR的增大而被加强，相应地，有限频率噪声谱上谷的深度被增加，如图2（b）中所示。

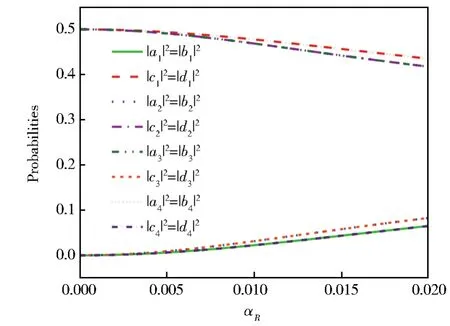
图5 形成4个单占据本征态的16个电子态的占据概率随着自旋轨道耦合参数αR的变化。其中，系统的其他参数与图2相同Fig.5 Probabilities of the sixteen electronic states of the four singly-occupied eigenstate as a function of the SOCαR.The other parameters are same to those for Fig.2

2.2 基于电流有限频率噪声谱定量获取自旋轨道耦合场的大小

对于串联耦合双量子点，其电流有限频率噪声谱中的峰、谷位置仅依赖于12个非对角元相应的能量本征值之差的绝对值。其中，当非对角元相应的能量本征值之差绝对值的简并度为2，其对应的是谷；而对于简并度为1的情形，对应于峰。由（19）—（22）式可知，两个峰和两个谷的位置可以表示为

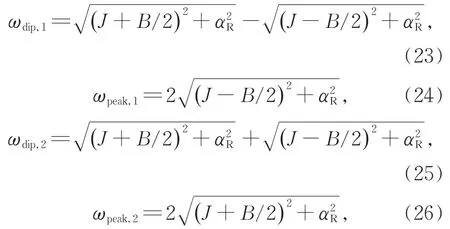
将（23）式乘以（25）式可得

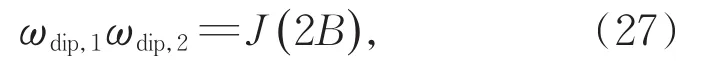
将（24）式的平方加上（26）式的平方可得

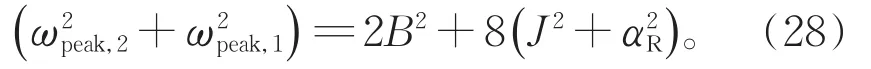
对于（27）式和（28）式，外加磁场B已知，自旋轨道耦合场参数αR和自旋守恒的电子跳跃隧穿强度J未知，因此，可以通过改变外加磁场B的大小，分别以2B和ωdip，1ωdip，2为横、纵坐标作图，此时，曲线的斜率即为J的大小。为进一步确定自旋轨道耦合参数αR，以2B2和为横、纵坐标作图，则曲线的截距为的大小。因而，由2B—ωdip，1ωdip，2曲线的斜率J和曲线的截距，可以确定串联耦合双量子点的自旋轨道耦合场参数αR。

3 结论

本文研究了自旋轨道耦合串联双量子点的电流有限频率噪声谱，并讨论了基于其峰和谷位置定量提取自旋轨道耦合场大小的理论方案。研究发现电流有限频率噪声谱中峰和谷的存在起源于串联耦合双量子点的量子相干性；峰和谷的位置取决于约化密度矩阵非对角元相应的能量本征值之差。其中，当非对角元相应的能量本征值之差的简并度为2时，其对应于谷；而对于简并度为1的情形，则对应于峰。因此，可以通过调节外加磁场的大小，基于电流有限频率噪声谱中峰和谷的位置，来确定量子点之间自旋守恒的电子跳跃隧穿强度和自旋轨道耦合场参数的大小。这些结果将有助于深入分析和全面理解基于自旋轨道耦合效应的电子自旋自由度操控。