基于聚类的标签集成传播算法

王锋，侯艳伟，魏巍*，崔军彪

（1.山西大学 计算机与信息技术学院，山西 太原 030006；2.山西大学 计算智能与中文信息处理教育部重点实验室，山西 太原 030006）

0 引言

传统的机器学习方法仅使用标记样本，即监督学习，这种学习方法的性能严重依赖于大量的标记样本。在现实应用中，收集大量的标记样本通常是昂贵的和耗时的。然而，获取未标记样本相对容易得多。为充分利用这些未标记样本完成学习任务，半监督学习算法［1］应运而生。半监督学习的优势在于能够通过少量的标记样本和大量的未标记样本，有效提高学习器性能［2-3］。

近年来，半监督学习的理论研究和实际应用取得了重大的发展［4］，基于图的标签传播算法是半监督学习中的重要研究方向［5］，这类算法在对数据分布缺乏先验知识的情况下，可以应用图论知识建立可解释性强的模型［6］进行学习。在过去，有许多学者致力于研究基于图的标签传播算法。Zhu等人［7］提出了一种基于高斯随机场模型的半监督学习方法。该方法是一种二分类方法，在进行多分类任务时还需对算法进行处理，但是从二分类到多分类的转化往往会导致次优的结果。Zhou等人［8］指出半监督学习的关键假设是先验一致性，在此基础上，通过图刻画样本之间的关系，将每个点的标签信息迭代地传播到其相邻节点，并给出了算法的正则化框架。Subramanya等人［9］提出一种基于KL散度损失的标签传播算法，有效解决了基于平方损失的图标签传播算法在高斯噪声下分类结果次优的问题。Kipf等人［10］将基于图的标签传播算法进行扩展，利用图卷积神经网络进行标签传播，该算法通过相邻节点的聚合实现了标签信息的传播。但使用随机梯度下降求解算法使其结果不稳定，并且在训练数据集较小时性能较差。这些算法都需要输入一个合理的图表示数据的分布，然而构造一个合理的图往往是很困难的。Sousa等人［11］研究了常用的构图方法对基于图的标签传播算法性能的影响，从实验的角度说明了在不同的图上进行标签传播，得到的分类结果存在很大差异。

上述分析表明基于图的标签传播算法的性能依赖于图的质量，高质量的图有利于标签传播算法的性能提升，反之，则有可能导致性能下降。虽然也有很多种方法可以用于计算图的邻接矩阵和边的权重，但对于一个具体的学习任务，如何构建一个高质量的图以提升标签传播的性能仍然是一个困难的问题。为了避免构图困难的问题，本文提出了一种新的标签传播算法，该算法首先采用聚类算法发现数据中潜在的分布结构，然后在聚类所得簇划分中进行标签传播。实验结果表明了提出算法的有效性。

1 基础知识

1.1 基于图的标签传播算法

设X＝Dl∪Du是给定的训练样本集，其中Dl＝{(x1，y1)，(x2，y2)，…，(xl，yl)}是标记样本集，Du＝{xl+1，xl+2，…，xl+u}是未标记样本集，其中l≪u，l+u＝m。半监督学习可以有效地利用少量标记样本的标签信息和大量未标记样本提供的分布信息［12-13］，提高模型的泛化能力。

基于图的标签传播算法是半监督学习的一种代表性方法，通常分为两步［14］：

第一步：基于样本集X构造一个图G＝(V，E)，V是点集，E是边集，其中每一个节点代表一个样本，每一条边代表两个样本之间的相似性，即节点集对应样本集X，边集对应权重矩阵W。

第二步：通过建立学习目标，确定优化问题，将标记样本的标签信息传播给未标记样本。基于图的标签传播算法的关键假设是相似的样本具有相似的标签，其学习目标是最小化关于图的标签不一致性，进而为未标记样本分配标签。

1.2 K-means聚类算法

K-means是一种经典的聚类算法［15］。对于给定的样本集，通过最小化每个簇内样本与该簇均值向量之间的距离，将样本集划分为K个互不相交的簇，即C＝{C1，C2，…，CK}。使得同一簇内样本之间的相似性尽可能大，而不同簇样本之间的相似性尽可能小。算法的优化目标是最小化平方误差，（1）式为其优化目标：

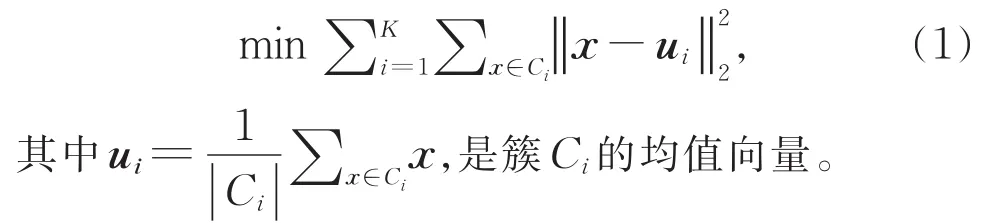
1.3 互补熵

Liang等人［16］将互补熵引入到信息系统的不确定性度量中，互补熵不同于Shannon提出的信息熵，互补熵考虑到了信息增益的互补行为。假设K＝(U，R)是一个近似空间，并且R是U上的一个划分，定义了粗糙集理论的互补熵，其公式定义如下：

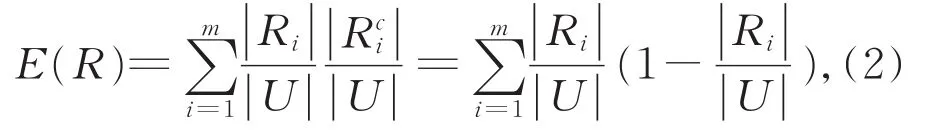
2 基于聚类的标签集成传播算法

聚类算法根据相似性将样本集划分为若干个簇，以达到同一个簇内的样本相似性大、不同簇内的样本相似度性小的目的［17-20］。在样本集的分布信息未知的情况下，利用聚类发现样本集潜在的分布结构，从而有效地实现标签传播，避免基于图的标签传播算法构图困难的问题［11］。因此，本文提出基于聚类的标签集成传播算法CLEP（Clusteringbased label ensemble propagation algorithm），该算法采用聚类的方法辅助标签传播。

2.1 CLEP算法的基本思想

首先，对输入的样本集X进行p次K-means聚类，每次K-means聚类算法将样本划分为K个簇C1，C2，…，CK，总共得到关于样本集的p个划分结果。然后根据每次聚类的簇划分结果进行标签传播，如果簇内有标记样本，并且该簇的标签混乱程度H(Ci)小于阈值，则将该簇内出现最多的标记样本的标签传播给该簇内的所有未标记样本。这样对p个簇划分结果进行标签传播，就得到p次标签传播结果，对这些标签传播结果根据投票机制进行标签集成，为未标记样本赋予一个鲁棒的预测标签。经过上述传播后，判断是否全部标签确定，若是，则输出未标记样本的预测标签；若不是，则重复上述聚类和标签传播的过程，直至所有未标记样本都被赋予标签。需要强调的是，当样本集中标记样本不增加的时候，需要调整K-means聚类算法的聚类簇数以求继续进行标签传播。

在CLEP算法中，每次K-means算法的时间复杂度为O(ntKm)，其中m为样本数，n为样本的属性数，K为K-means算法中的聚类簇数，t为K-means算法中的簇中心更新过程的迭代次数。算法首先对样本集进行p次K-means聚类的时间复杂度为O(pntKm)。接下来的标签传播过程的时间复杂度为O(pKL)，其中L为样本的实际类别数。CLEP算法是一个聚类和标签传播迭代进行的算法，通常情况下，样本数m远大于实际类别数L，所以本算法的时间复杂度为O(TpntKm)，其中T为聚类和标签传播的迭代次数。

2.2 算法的关键步骤介绍

（1） 簇内样本的标签混乱程度度量

在簇内标签混乱的情况下，不适合将某种标签传播，即使某种类标签占了多数。因此，需要根据簇内样本的标签混乱程度判断簇内是否可以进行标签传播。

本文采用互补熵度量聚类得到的簇内样本的标签混乱程度，互补熵越大，簇内样本的标签混乱程度越大，越不适合进行标签传播。互补熵公式如下：

（2） 簇内标记样本的标签投票

在CLEP算法中，通过K-means聚类对样本集进行簇划分，对产生的每个簇采用投票的方式选出占有数量优势的标记样本的标签，如果该簇只有一种标签有数量优势，并且该簇的标签混乱程度较低，则就可以将这种标签赋予该簇的所有未标记样本。

（3） 基于投票机制的标签集成

在每一轮标签传播中，都要进行p次K-means聚类，产生p个对样本集的划分，每个划分可以产生一种对于未标记样本的标记结果，所以每一个未标记样本xi，都可以得到p个标记结果，这些结果可能是相同或不同的标签，也可能是没有标签。对于一个样本，如果p次标签传播的结果中获得某个标签lp的次数大于p/2，则将这个样本标记为lp。

2.3 算法详细描述

基于上述分析，给出算法的详细描述。

算法1基于聚类的标签集成传播算法

输入：标记样本集

Dl＝{(x1，y1)，(x2，y2)，…，(xl，yl)}

未标记样本集Du＝{xl+1，xl+2，…，xl+u}

混乱程度阈值θ

聚类算法的聚类簇数K

过程：

1初始化参数，传播标签数c1和c2等于0

2 whilec2＜u

3使用聚类簇数为K的K-means聚类算法对样本集进行p次聚类

4 fori＝1，…，pdo

5 forj＝1，…，Kdo

6找出Ci簇内数量最多的标记样本的标签集合B

7 if|B|＝1

8 ifH(Cj)＜θ

9进行标签传播，将未标记样本的标签都预测为集合B中标签

10 end if

11 end if

12 end for

13 end for

14 fori＝1，…，u

15使用标签集成机制对样本xl+i的p次标签传播结果进行集成

16Dl＝Dl∪{xl+i}，Du＝Du{xl+i}

17c2＝c2+1

18 end for

19 ifc1＝c2

20K＝K—1

21 end if

22c1＝c2

23 end while

输出：所有未标记样本的预测标签

对于以上算法，当标签传播的过程进行到一定阶段时，由于某些样本始终不能被划分到包含标记样本的簇中，因此这些样本不能被标记，造成算法无法结束。针对这一问题，可以通过将聚类簇数K适当减小（见算法19—21行），以增加样本簇的大小，从而使得那些不能被标记的样本所在的簇能够拥有一些标记样本。

3 实验分析

3.1 实验数据

为了验证提出算法的有效性，在5个UCI数据集上进行实验，其中2个二分类数据集，3个多分类数据集。数据集的信息描述如表1所示。

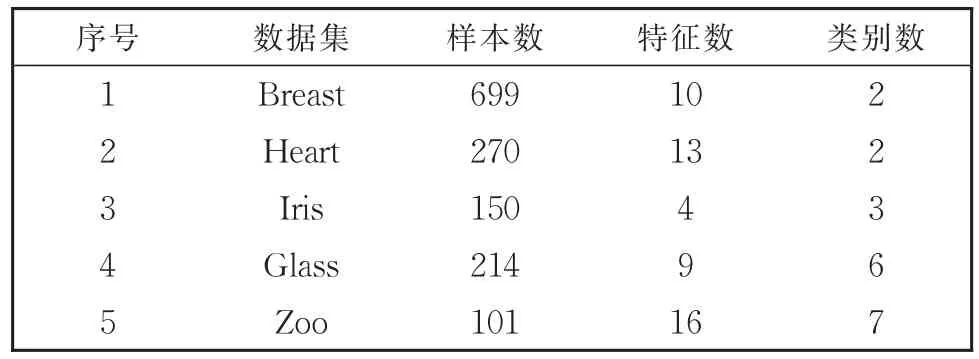
表1 数据集描述Table 1 Description of data set

3.2 实验结果

本节分为两部分：（1）K-means聚类算法的聚类簇数K对实验结果的影响；（2）提出算法与4种经典的基于图的标签传播算法的效果对比。

在实验中，为了减小实验结果的随机性，所有实验结果均为随机取30组标记样本进行实验得到的平均分类准确率。

首先，分析聚类簇数K对实验结果的影响。CLEP算法中的聚类簇数K是指聚类算法得到簇划分的个数，用于调节簇的大小，K越大，得到的簇就越小，K越小，得到的簇就越大。在我们的算法中，当聚类和标签传播进行到一定阶段时，会出现某些簇不包含标记样本的情况，导致这些簇内的未标记样本无法获取标签。通过减小K，可使聚类得到的簇变大，簇内出现标记样本，进而实现标签在簇内继续传播。

在这部分实验中，有10%的样本的标签是已知的，需要对剩余的90%的未标记数据进行标签预测。图1的折线图所示为在5个数据集上取不同的聚类簇数对应的分类准确率。在Breast数据集和Heart数据集上聚类簇数K等于样本实际类别数时，分类准确率达到最高，之后随着聚类簇数K的增大分类准确率下降。对于剩余的3个数据集，由于每个数据集的样本总量相对少，样本类别相对多，每种类别数据量较少，分类准确率随着聚类簇数的增大而增大。因此，提出的CLEP算法中的聚类簇数K的建议取值为实际类别数L到（）范围内的整数（m的取值为样本数）。这样的参数建议取值是根据CLEP算法在本文所用的5个数据集上的实验结果得出的。

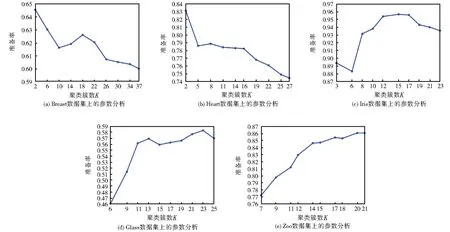
图1 CLEP算法的参数分析Fig.1 Parameter analyses of CLEP algorithm.

然后，将提出的CLEP算法与其他算法进行实验对比。提出的算法是一种标签传播算法，为了验证算法效果，将提出的算法与4种经典的基于图的标签传播算法进行对比，这4种算法分别是：GFHF［7］、LGC［8］、MP［9］、GCN［10］。GFHF 算法无超参数，LGC算法依据文献［8］的推荐将超参数设置为α＝0.99，MP算法［9］中依据文献［9］在合成2维双月数据集上的参数取值，将参数设置为μ＝0.2，ν＝0.001，α＝1。GCN算法［10］的实验结果是将隐藏层神经元个数设置一定的取值范围进行实验，取最好的实验结果得到的。CLEP算法聚类簇数K的取值在实验结果表中给出。

在4种对比算法中，均采用5-NN构图法建立对称连接图，余弦相似度加权，权重矩阵W的定义如下：

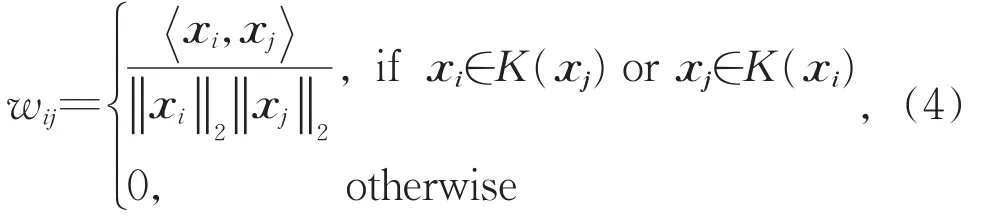
GFHF算法是二分类算法［7］，所以在多分类数据集上未进行实验。从表2的实验结果中可以看出，在Breast数据集上，不同比例的标记样本对应的8组实验中，CLEP算法的效果均优于对比算法，并且提出的CLEP算法在标记样本比例为5%的时候就已达到最佳的对比算法LGC在标记比例为35%时的效果。从表3的结果可以看出，在Heart数据集上，CLEP算法虽然随着标记样本的增多准确率几乎不变，但是依然优于对比实验的效果。表4为Iris数据集上的结果，除了标记比例为40%的时候效果领先不明显外，其余7组实验结果都有较为明显的领先。表5和表6的实验结果中，CLEP算法性能均优于对比算法，特别地，在Zoo数据集上标记比例为5%时，相对性能最好的LGC算法准确率有0.09的提升。从实验结果中可以看出，CLEP算法的分类准确率优于所有对比算法，特别是在标记样本比例较低时，优势更为明显。这一实验结果表明，本文提出的算法更适合标记样本缺乏情况下的学习任务。

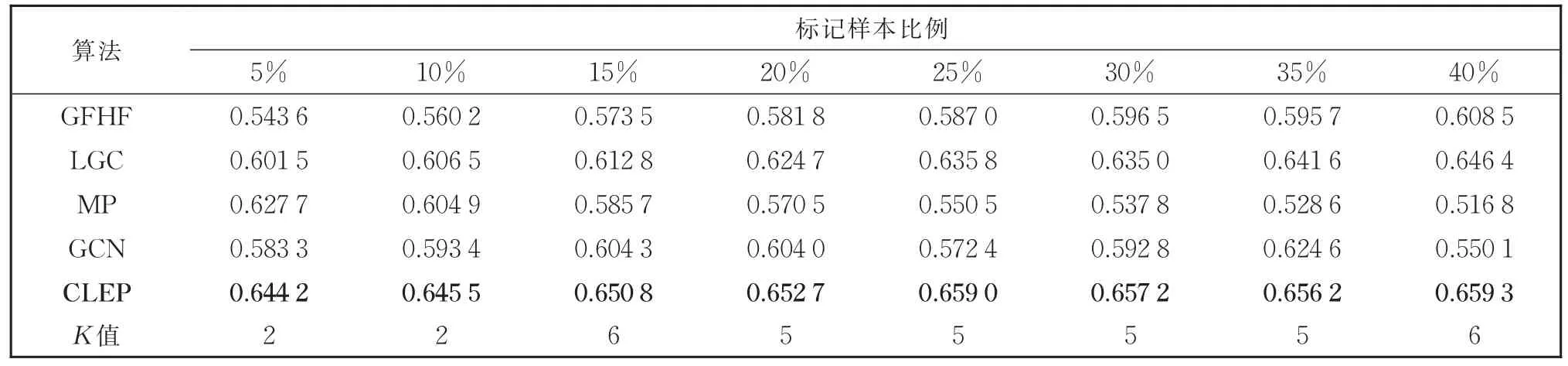
表2 提出算法与基于图的标签传播算法在Breast数据集上的分类准确率Table 2 Classification accuracy of the proposed algorithm and the graph-based label propagation algorithms on the Breast data set

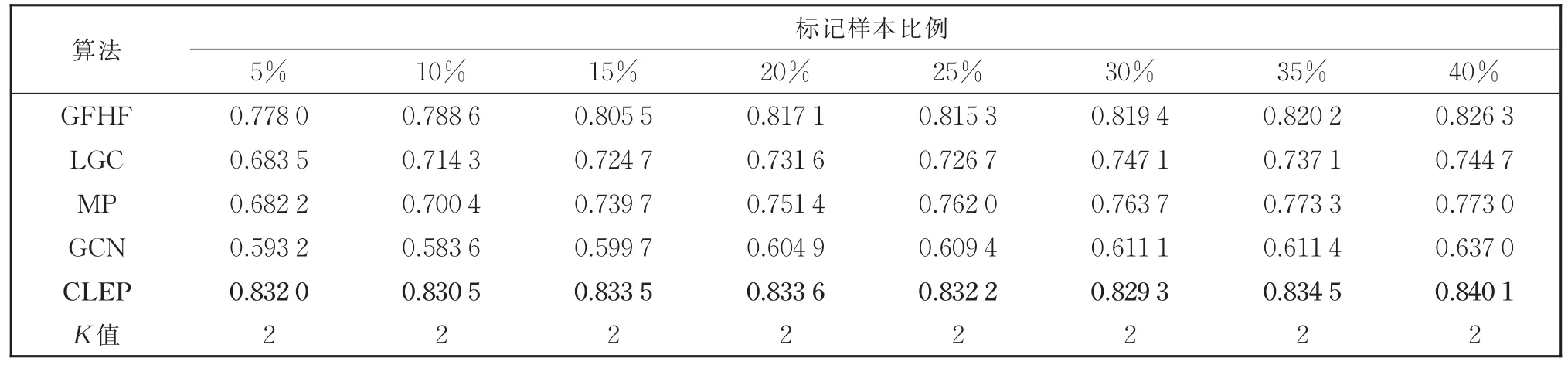
表3 提出算法与基于图的标签传播算法在Heart数据集上的分类准确率Table 3 Classification accuracy of the proposed algorithm and the graph-based label propagation algorithms on the Heart data set

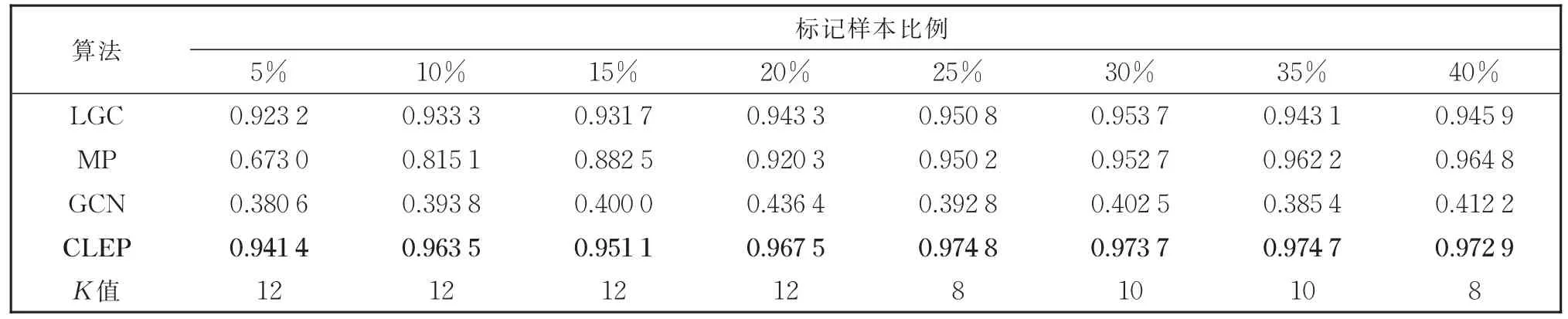
表4 提出算法与基于图的标签传播算法在Iris数据集上的分类准确率Table 4 Classification accuracy of the proposed algorithm and the graph-based label propagation algorithms on the Iris data set

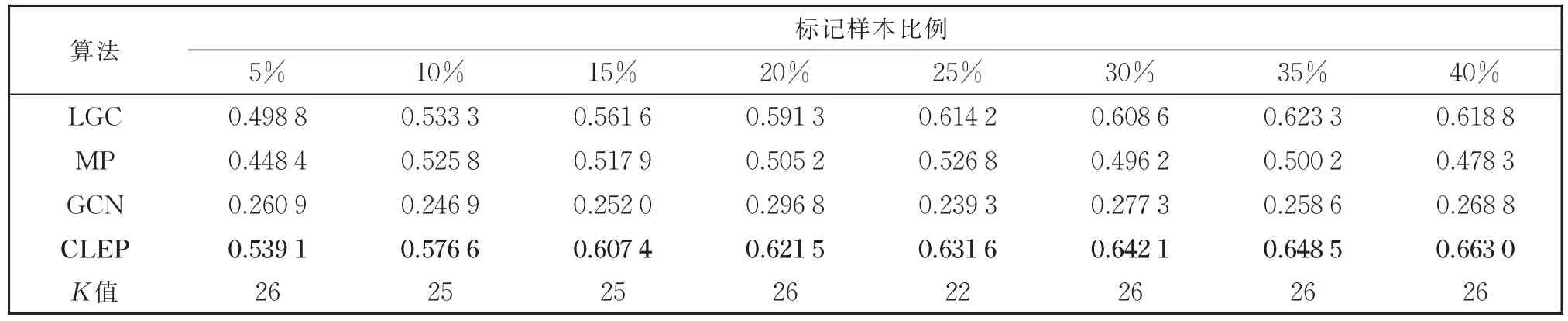
表5 提出算法与基于图的标签传播算法在Glass数据集上的分类准确率Table 5 Classification accuracy of the proposed algorithm and the graph-based label propagation algorithms on the Glass data set

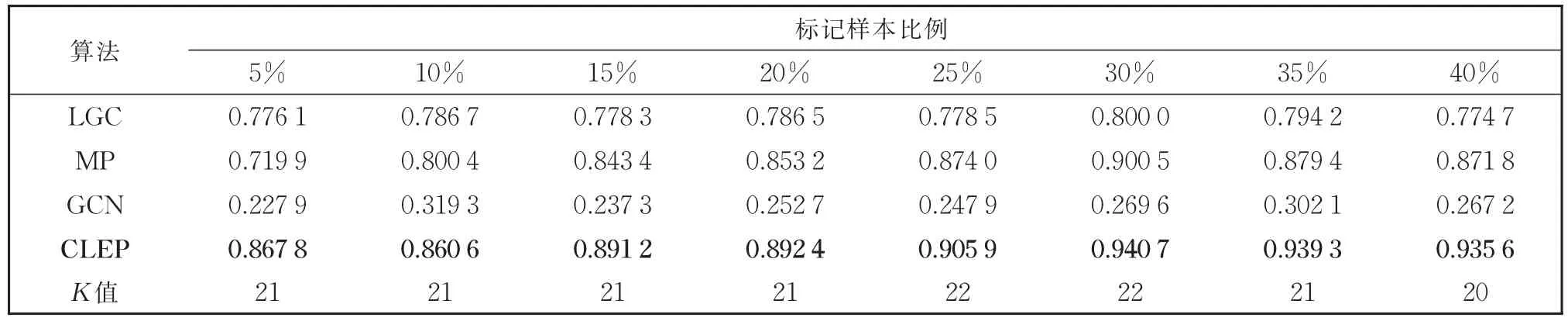
表6 提出算法与基于图的标签传播算法在Zoo数据集上的分类准确率Table 6 Classification accuracy of the proposed algorithm and the graph-based label propagation algorithms on the Zoo data set

4 结论

本文提出了一种基于聚类的标签集成传播算法，该算法首先利用聚类方法对数据集进行若干次簇划分，然后在标签混乱程度较低的簇中，将占有数量优势的标签赋给未标记样本，然后对若干个标签传播的结果进行集成，赋予未标记样本一个鲁棒的标签，迭代运行上述步骤，直至所有未标记样本被赋予标签。基于聚类的标签集成传播算法避免了基于图的标签传播算法中的构图问题，在缺乏数据分布信息的情况下实现标签传播。实验结果表明提出的算法在分类精度上优于所有对比算法。本文提出的CLEP算法是在K-means聚类算法所得的簇中进行标签传播，所以聚类效果对标签传播的结果有一定影响。CLEP算法采用K-means算法不能较好的识别非凸数据集。在后续的研究中，可关注如何设计更好的多个聚类算法促进标签传播，提升分类效果。