小波分解与Prophet框架融合的电离层VTEC预报模型

田 睿,董绪荣

(航天工程大学航天信息学院,北京 101407)

0 引 言

在导航定位、无线通信、航空航天、气象预测等领域,电离层对电磁波的折射、散射、反射和吸收效应影响巨大[1-5]。在全球导航卫星系统(global navigation satellite system,GNSS)领域,电离层垂直总电子含量(vertical total electron content,VTEC)是直接决定电离层延迟误差的重要参数,尤其在单频精密定位的实时应用中,须构建高精度的电离层延迟预报模型对电离层延迟进行实时修正。因此,研究电离层VTEC预报具有重要的应用价值[6]。目前,应用比较广泛的电离层模型大多是传统经验模型,如IRI、Klobuchar、Bent等模型。但传统经验模型的应用效果并不十分理想[7],如常用的Klobuchar模型的预报精度仅为50%～60%。因此,国内外学者提出了多种电离层VTEC预报方法,如时间序列、神经网络等[8-14]。其中,相比于其他预报方法,时间序列法具有短期预报精度高、计算简单、理论完备、样本数据要求较少等优势[15]。因此,在电离层短期预报领域,精度较高且相对简单的时间序列法受到了广泛关注。李秀海等学者最早引入了自回归(autoregressive,AR)模型来构建电离层VTEC时序预测模型,但AR模型难以准确地拟合VTEC时序数据的周期性变化,预测精度较低[16]。相比于AR模型,差分AR移动平均(AR integrated moving average,ARIMA)模型对时间序列的周期性变化及趋势项拟合较好,更适用于包含季节性变化及短期趋势项的电离层VTEC时序数据,其预测精度明显提升,因此目前大部分研究均以ARIMA模型为基础[15,17-19]。然而,由于电离层受地磁扰动、太阳活动、日地相对距离等环境因素影响较大[20],特别是在磁暴期间,受到强地磁扰动的影响,电离层VTEC的周日变化更为显著[21]。而在采用ARIMA模型进行预报时,受磁暴等复杂因素影响,电离层VTEC时序数据的非平稳性特征与非线性特征显著增强,大幅降低了ARIMA模型的预报精度。对此,翟笃林等学者[22]基于2017年Facebook开源的Prophet框架[23]进行了电离层VTEC的短期预报与异常探测,实验证明基于Prophet框架的预测精度明显优于ARIMA模型。相比于其他时间序列预测方法,Prophet框架不仅有较理想的预测精度,还具有:① 无需复杂的特征工程;② 可自动处理缺失值;③ 支持大规模细粒度数据;④ 调参简单;⑤ 考虑了节假日效应与特殊事件的影响;⑥ 可解释性强等一系列优点。然而,如何将Prophet框架与其他算法进一步融合,提高预测精度,是当前Prophet框架研究中亟待解决的问题[23]。

为进一步改进基于Prophet框架的电离层VTEC短期预报模型,提高预测精度,本文将小波分解与Prophet框架相融合,并综合考虑了地磁扰动对电离层的影响,提出一种小波分解与Prophet框架融合的时间序列预报模型以进行电离层VTEC短期预报。同时采用国际GNSS服务(international GNSS service，IGS)发布的GIM格网数据进行对比实验,验证改进模型的预报精度与适用性。

1 小波分解与Prophet框架融合的时间序列预报模型

为更详尽地阐述本文所提改进模型,将在第1.1节～第1.4节中首先对相关概念进行简要介绍,并在第1.5节中详细地阐述本文改进模型的基本架构与具体步骤。

1.1 小波分解基本原理

(1)

则Vj中任意函数fj均存在如下的多分辨表示:

(2)

可通过Mallat塔式算法对一维离散时间信号(序列)进行小波分解,分解过程的表达式为

(3)

X=Aj+Dj+Dj-1+…+D1

(4)

1.2 Prophet框架

Prophet框架的基础模型是一个由季节项、趋势项、节假日或特征事件影响(节假日效应)、误差项4部分组成的时间序列广义加法模型(可通过用户设置调整为乘积季节性模型),广义加法模型的表达式为

y(t)=g(t)+s(t)+h(t)+εt

(5)

式中,y(t)为时间序列在时刻t的取值;g(t)为趋势项,用于拟合时间序列的非周期变化;s(t)为季节项(或称周期项),用于拟合时间序列各种周期性变化(应注意,当设置为乘积季节性模型时,s(t)为对数形式);h(t)表示节假日效应特征事件的影响,通过该项,节假日或特征事件的影响可作为先验信息融入到模型中;εt为误差项(或称噪声因子),假设其服从正态分布。Prophet框架仅以时间作为自变量,且无需复杂的特征工程即可得到趋势项、季节项及节假日效应等组分。可解释性强,明确解释了目标序列的时间依赖结构[25]。

1.2.1 趋势项模型

Prophet框架中有两种趋势项预测模型:饱和增长模型与分段线性模型。饱和增长模型基于逻辑回归函数进行预测,其预测结果的增长趋势与人口增长的趋势类似,适用于预测一定承载能力下的非线性饱和增长。所谓承载能力即增长可到达的最大极限值。饱和增长模型的表达式如下：

(6)

式中,C(t)为承载能力;k为增长率;m为偏移量。应注意该模型与普通的逻辑回归函数有两处不同:① Prophet框架中的承载能力C(t)不是一个常数,而是随时间迁移而变化,需要人为给定该参数的值;② 增长率k也并非常数,Prophet框架通过给定变异点在模型中引入增长趋势的变化。

Prophet框架中的变异点位置可由用户根据先验信息人为指定,也可由Prophet框架自动选取。默认设置下,Prophet首先确定大量潜在的变异点,然后对潜在变异点上趋势变化的幅度做稀疏先验(等同于L1正则化)来选取变异点。实际上Prophet在建模时会识别出很多增长率k发生突变的潜在变异点,但会尽可能少地使用。按照默认设置,Prophet会在前80%的时间序列数据中识别出25个变异点。

假设Prophet在序列中确定了S个变异点,变异点位置在时间戳sj(j=1,2,…,S)上,也即在时间戳sj上增长率k发生改变。定义增长率变化向量δ∈RS,δ中的元素δj表示时间戳sj处增长率的变化。设序列初始增长率为k,某时间戳上sj的增长率可表示为

(7)

式中,αj(t)为向量α(t)中的元素,则在任意时刻t,k(t)可表示为k+αT(t)δ,进而可定义向量α(t)中的元素为

(8)

由于变异点导致了趋势项的非连续性,须对偏移量m进行自适应调整。则在变异点对应的时间戳sj处,通过下式对偏移量进行调整:

(9)

此时偏移量调整为m+αT(t)γ,并最终得到饱和增长模型:

(10)

用于表示时间序列的趋势项。而许多时间序列的趋势项并不符合饱和增长趋势,对此,Prophet框架采用更简约的分段线性模型对其趋势项进行拟合:

g(t)=[k+αT(t)δ]t+[(m+αT(t)γ)]

(11)

应注意,增长率变化向量δ满足δ～Laplace(0,τ)。其中,参数τ是本文主要调整的超参数,因为其直接控制趋势项增长率变化的灵活性。增大该参数会使趋势拟合更加灵活,但存在过拟合风险。

1.2.2 季节周期性

为对时间序列的季节性(或称周期性)进行精确建模,Prophet框架采用离散傅里叶级数对时间序列的季节项进行建模:

(12)

定义向量X(t)为

X(t)=

(13)

则可将季节项s(t)表示为X(t)与一个参数向量β的点乘形式为

s(t)=X(t)β

(14)

式中,β用于对模型季节性进行平滑,起到类似L1正则化的作用,其服从正态分布,即β～Normal(0,σ2)。可通过增大参数σ的值以适应更大的季节性波动,较小的σ则会抑制季节性效应,其默认值设置为10,该值在一般问题中通常是适用的[23]。在默认设置下,Prophet框架的参数估计方法为最大后验概率估计(简称为MAP),仅能得出趋势不确定性及观测噪声的影响,用户可通过设置mcmc.samples参数,采用马尔可夫链蒙特卡罗取样得到季节的不确定性。

1.2.3 节假日或特殊事件影响

考虑到节假日或特殊事件对时序数据的影响,Prophet框架在模型中将节假日效应h(t)作为先验知识融入到模型中,并认为节假日效应对时间序列的影响是独立的。应注意,节假日或特殊事件需要作为先验信息由用户给定。设节假日或特殊事件i对应的日期列表为Di,如十一黄金周对应的日期列表Di中包含10月1日到10月7日7个日期。Prophet框架通过一个指示函数表示某时刻t是否处于节假日或特殊事件i期间,同时需要一个参数κi来表示节假日及特殊事件的影响,设节假日或特殊事件i共包含L天,则节假日效应可表示为

(15)

式中,矩阵Z(t)表示为[1{t∈D1},1{t∈D2},…,1{t∈DL}];矩阵κ表示为[κ1,κ2,…,κL]T,κ～Normal(0,υ2),其中υ默认值设定为10,该值取值越大表示节假日对模型的影响越大;该值越小表示节假日对模型影响越小,用户可根据先验知识调整该值。

1.3 分解-集成模型

在时间序列预测中,常采用分解时间序列的方法对现有模型进行改进,即构建分解-集成模型[26],以提升预报精度。常采用的方法有STL分解、EMD分解等[27]。其中,小波分解作为分析非线性及非平稳信号的重要数学工具[28-29],适合处理具有非线性、非平稳特征的电离层VTEC时间序列,在对ARIMA模型的改进中取得了良好的效果,如刘立龙等学者[30]及鲍亚东等学者[31]均引入了小波分解以改进ARIMA模型,提高了电离层VTEC短期预报精度。

基于小波分解构建的分解-集成模型能提高预报精度的原因在于:小波分解实现了时间序列的时频局部化,充分挖掘了时间序列中包含的信息[32]。因此,可通过小波分解有效地分离和提取时序数据的周期性、非线性及变化趋势[33],使预测模型能够更好地对时序数据的周期性变化、变点信息及趋势项进行拟合与建模,从而得到更为精确的预测结果。

而电离层VTEC时序数据可视作非平稳非线性的离散时间信号(序列),通过小波分解对其进行多分辨分析。分解所得的低频分量包含了信号的主体信息,而不同分辨率的高频分量则描绘了信号的细节纹理。因此,可利用小波分解快速高效地对电离层VTEC时间序列的各分量进行分离,使样本序列的周期性变化、变点信息和短期趋势更加显著,预测模型能够更好地对其拟合与建模,从而提高预测精度[30]。

1.4 小波基的对比及选取

小波基的选取问题一直是小波技术应用中的难题,众多学者针对各自的应用需求提出了不同的选取方法[34-36],本文将首先对各种小波基的特性进行分析,并结合电离层VTEC时序数据的特点,通过理论分析与实验相结合的方式进行小波基的选取。

一般而言,小波基具有5个重要特性[37]:正交性(或双正交性)、对称性、正则性、消失距和紧支撑性。正交性反映了小波基的完善程度,规范的正交性有利于信号的精确重构;较好的对称性可避免信号分解与重构时的相位失真;正则性表征小波基的可微性,较好的正则性有利于捕获信号的奇异点,大部分正交小波基正则性越高则消失距越高[38];消失距反映了小波变换后的能量集中程度,支撑宽度反映了小波的局部化能力,支撑越小,小波基局部化能力越强[39],而支撑越大,正则性越好。常用小波基的各项特性如表1所示。

表1 常用小波基的各项特性Table 1 Characteristics of commonly used wavelet bases

结合前文所述的电离层VTEC时间序列的特点及小波分解的作用,适合本文应用场景的小波基应满足如下要求:① 规范的正交性,应选择具有规范正交性的小波基,有利于小波分解后的精确重构。② 较高的消失距,如前文所述,较高的消失距即意味着较好的正则性。这有利于捕获序列中的奇异点(有利于Prophet框架中的变异点建模),充分挖掘电离层VTEC时间序列包含的信息,便于拟合与建模。③ 适中的支撑长度,如前文所述,支撑越小,小波基局部化能力越强,而支撑越大,正则性越好。

基于上述要求,本文排除了Haar、mever、morlet等小波基,并将在Daubechies、Symelets、Coiffets 3种小波基中选取合适的小波基。

如前文所述,小波分解提高预报精度的原因可简要概括为:小波分解可充分挖掘序列包含的信息,使样本序列的周期性变化、变点信息或短期趋势更加显著,利于建模和预测。因此,为对上述小波基的分解效果进行对比,本文基于最大信息熵原理对分解效果进行评估,该原理广泛应用于时间序列的分析与预测中[40-42]。最大信息熵原理指出:在满足所有已知条件的情况下进行预测,应选择信息熵最大的可行解,这样所得的解最为客观、超然且偏差最小[43]。杨薛明等学者即应用此原理,引入信息熵作为优选样本序列的依据[42]。本文计算了上述小波基分解所得子序列的信息熵,并基于最大信息熵原理进行小波基的选取。

实验过程、结果及分析详见第2.2节,本文最终选用db4小波基,取得了良好的改进效果,这也与文献[30-31]的结论相印证。

1.5 改进模型的架构与步骤

本文提出了一种小波分解与Prophet框架融合的时间序列预报模型以进行电离层VTEC短期预报,其总体架构如图1所示。

图1 改进模型的总体架构Fig.1 Overall architecture of the improved model

如图1所示,本文所提改进模型的基本思路是:首先按第1.1节中的方法对电离层VTEC时间序列进行小波分解,得到近似分量Aj和一组细节分量D1,D2,…,Dj,并分别基于Prophet框架对其进行预测。最后,对预报序列进行重构得到最终预测结果。该模型是一个典型的分解-集成模型[26]。

为进行电离层VTEC的期预报,除预测模型外,还必须考虑样本数据的采集与预处理、超参数的调节、模型的性能度量等方面的内容。因此,对基于本文改进模型进行电离层VTEC短期预报的具体步骤如下。

步骤 1分别选取平静期和活跃期时段,下载IGS发布的GIM格网数据文件(IONEX格式文件)。同时,从国家空间科学数据中心上下载对应时段的地磁指数数据,并从空间环境预报中心上下载相应的历史预报产品。

步骤 2选择格网点,参考日本东京海洋大学开发的开源软件RTKLIB中的相关源码,按照一定的时间粒度,编程提取目标格网点的VTEC值,获得原始时间序列数据。

步骤 3由于GIM格网数据具有可靠的精度和稳定性,常作为基准数据使用[44]。因此,无需处理缺失值与异常值。应注意,其中明显区别于一般数据的VTEC值并非错误值,不应作为“异常值”处理,最终得到实验数据集。

步骤 4将实验数据集输入模型,同时根据下载的地磁指数数据以及历史预报产品,构建特殊事件(如磁暴等)列表作为先验信息输入模型,从而在模型中引入地磁扰动的影响。以均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)和平均百分比误差(mean absolute percentage error,MAPE) 3项指标评估预测结果，并综合采用网格搜索法自动调参、可视化技术实时交互式调参等方法调整模型参数。

步骤 5最后经过多次迭代调参,可获得较优的最终模型,得到预测结果,并对最终模型的预测结果进行评估。

在特殊事件列表的构建过程中,已知时段的特殊事件通过国家空间科学数据中心上下载的地磁指数数据来确定,而预报时段的特殊事件则通过空间环境预报中心上下载的历史预报产品确定。这与实际应用场景相符合,如已知11天的电离层VTEC数据,预测步长为3天,即以11天的已知数据作为实验数据集进行预测。在这11天的已知时段上,可通过已知的地磁指数数据来确定特殊事件列表,而在未来3天的预报时段上,则仅能通过预报产品确定特殊事件列表。

2 实验及分析

2.1 原始数据及先验信息的获取与分析

GIM格网数据的时间分辨率为2 h,一天的数据包含13张全球电离层格网地图,空间分辨率为2.5°(纬度)×5°(经度)。参照文献[30]中的实验方法,本文的实验区域集中于中国以及周边国家和地区,如表2所示。

表2 实验区域Table 2 Experimental area

本文按照经度间隔10°、纬度间隔7.5°选取格网点,共计54个格网点,并在单个格网点上按每天时段为00:00～22:00,以2 h为间隔提取VTEC数据。实验数据的时段选择上,根据文献[15],本文选取2010年2月16日至3月1日(年积日47～60日)进行活跃期电离层预报实验;选取2008年2月1日至2月14日(年积日32～45日)进行平静期电离层预报实验。参照文献[15]及文献[30]的实验方法,以每个时段前11天数据作为实验用数据集,预测步长为3天,并以GIM格网数据为基准对预报结果进行评估。

如前文所述,特殊事件列表将作为先验信息输入模型,并选取地磁指数Ap作为衡量地磁活动指标。其中地磁指数Ap表示行星等效日幅度,可作为全天地磁活动水平的度量[45]。为说明磁暴等特殊事件的确定方法,获取建模所需的先验信息,对活跃期时段的地磁扰动强度进行分析。活跃期时段扰动暴实时(disturbance storm time,DST)与地磁指数Ap的变化,如图2所示。

图2 年积日47～60天的地磁指数Ap与DST指数Fig.2 Geomagnetic Ap and DST Index (DOY 47～60)

DST指数表征环电流强度,当DST指数小于-30 nT时即可能发生小磁暴,小于-50 nT时即可能发生中等磁暴[30]。如图2所示,年积日47～48日多个历元DST指数较低(可能发生中小磁暴),与之对应的地磁指数Ap均达到或超过5。即可根据地磁指数Ap判断某日的地磁扰动是否剧烈,并构建特殊事件列表,作为先验信息输入模型。根据图2,预测时段内地磁扰动并不剧烈,预测中无需考虑特殊事件的影响。

图3 活跃期格网点(32.5°N,75°E)的原始样本序列小波分解结果Fig.3 Wavelet decomposition results of the original sample sequence of lattice nodes (32.5°N,75°E) in the active period

如前文所述,本文改进模型还需要对输入的样本序列进行小波分解,以往研究常采用1～3级分解[12,28-31],分解层数过多会造成累积误差过大。本文经实验证明,一级分解的预报结果精度最高,且编程实现简单,更重要的是避免了多层分解中误差的累积,这也与文献[30]中的结论相印证[30]。限于篇幅,图3仅给出了活跃期时段格网点(32.5°N,75°E)的原始样本序列小波分解的结果。

2.2 小波基选取实验

根据第1.4节的有关讨论,本文将基于GIM格网数据,对sym4、db4、sym8、db8、sym12、db12、coif2和coif3等小波基进行实验对比,并从中优选适用的小波基。

本实验基于上述小波基,依次对不同时期不同格网点对应的原始样本序列进行小波分解。然后,计算子序列的信息熵,并基于最大信息熵原理进行小波基选取。由于对电离层活跃期数据进行预报的难度较大,选取时将优先考虑活跃期的性能。不同时期不同实验区域的分解序列信息熵均值,如图4所示。分解所得的序列信息熵差异主要表现在高频分量上,这是因为信号的细节纹理主要包含在高频分量中[30]。由图4可见,db4小波基分解所得的子序列信息熵均值在不同时期、不同实验区域内均较高,特别是在中纬度区域显著高于其他小波基。则根据第1.4节的有关讨论,基于最大信息熵原理,本文拟选用db4小波基。

图4 不同时期不同实验区域的分解序列信息熵均值Fig.4 Mean information entropy of the decomposition sequences in different experimental regions and different periods

2.3 模型精度及适用性分析

2.3.1 模型评估指标

如前文所述,采用RMSE、MAE和MAPE 3个性能度量指标对模型结果进行评估。

RMSE计算公式为

(16)

MAE计算公式为

(17)

式中,MAE表示实际输出值与预测值绝对差值的平均值。MAE取值越小,说明模型精度越高。

MAPE计算公式为

(18)

式中,MAPE取值越小,说明模型精度越高。

2.3.2 模型参数设置

根据电离层VTEC时间序列的性质[15,30]可知,在短期预报中,序列的周期性变化以比较规律的周日变化为主,序列的周期无明显改变,周期的不确定性并不显著。因此,与周期有关的模型参数均设置为Prophet框架的推荐值,上述推荐值在一般问题中通常是适用的[23]。同时,在变异点筛选中,采用Prophet框架的自动筛选[23],这一方面提高了建模的客观性,另一方面降低了建模难度。然而,在电离层VTEC时间序列的短期预报中,序列的趋势项变化较为剧烈,特别是在电离层活跃期的中低纬度地区。如前文所述,超参数τ直接控制趋势项增长率变化的灵活性。增大该参数会使趋势拟合更加灵活,但也存在过拟合风险。因此,本文采用网格搜索法,基于外推结果的RMSE值对参数τ进行调优。如前文所述,在本文提出的改进模型中,需利用Prophet框架对高频分量与低频分量分别进行预测。对两种分量的预测需要设置不同的参数τ。因此,采用网格搜索法对改进模型进行调参,参数取值范围设置为0.05～0.95,搜索步长设置为0.05,结果如图5所示。基于以上网格搜索结果并进行人工微调后,实验中改进模型的参数设置如表3所示。

图5 改进模型超参数τ的网格搜索结果Fig.5 Grid search results for the hyperparameter τ of the improved model

表3 参数设置Table 3 Parameter settings

2.3.3 实验结果分析

按照前文所述实验方法,分别采用本文改进模型、未改进的Prophet框架、ARIMA模型进行对比实验,并对预测结果进行统计,即可计算RMSE、MAE和MAPE 3项指标。在电离层平静期与活跃期,不同实验区域内各项指标的均值分别如表4和表5所示。

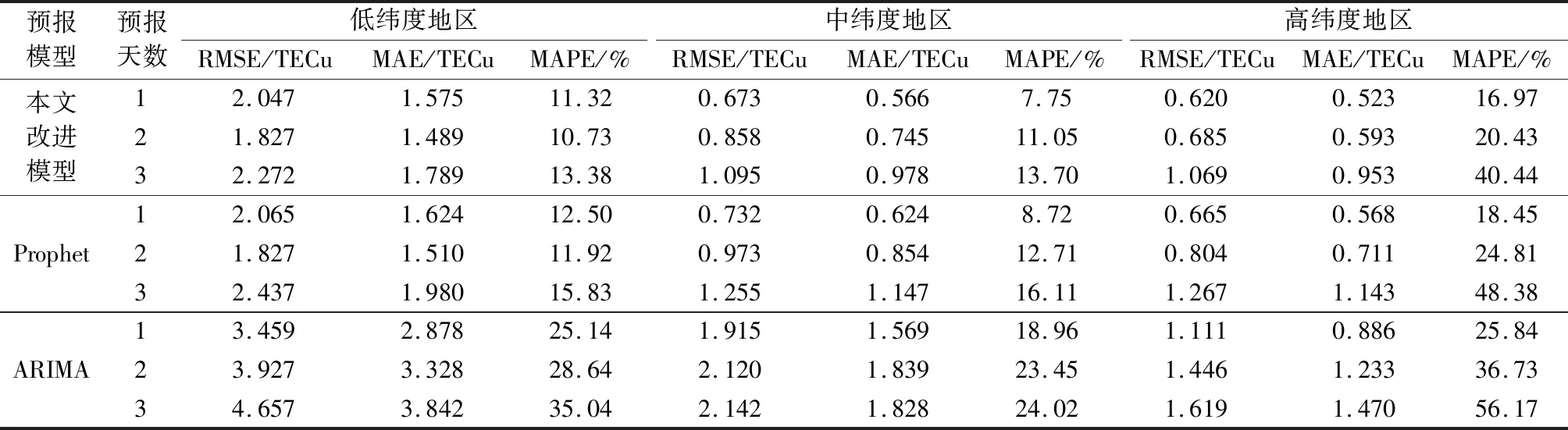
表4 电离层平静期不同实验区域内各项指标的均值Table 4 Mean values of each index in different experimental areas during the ionosphere quiet period

表5 电离层活跃期不同实验区域内各项指标的均值Table 5 Mean values of each index in different experimental areas in the ionosphere active period

如表4和表5所示,无论在电离层平静期还是活跃期,本文改进模型在低、中、高纬度3个实验区域的预测误差均比较小,且各项评估指标的均值优于未改进的Prophet框架,这验证了本文改进的有效性。同时,本文改进模型与未改进的Prophet框架明显优于传统的ARIMA模型,这也与文献[22]中的结论相印证[22]。

表4与表5进行对比可知,在电离层活跃期,3种模型的预测精度均有所下降,各项指标大多明显增加。这是因为在电离层活跃期,受到地磁活动以及日地相对距离、太阳活动等复杂的不确定因素影响,电离层VTEC周日变化更加剧烈,导致时间序列的非平稳性与非线性特征显著增强,造成建模难度增大,预报精度受到严重影响。类似的,由于VTEC的周日变化幅度随纬度降低而总体增大,其非平稳性非线性特征更加显著,由表4和表5可知,低纬度地区预报精度普遍低于中、高纬度地区,且改进的效果相对较差,这是因为序列的非平稳性受各项复杂因素影响显著增大,增加了分解难度与累积误差。总体而言,本文改进模型在中、高纬度地区适用性更好。

由于表4和表5给出的是实验区域内所有格网点的均值,不能反映各格网点上的预测效果。RMSE能够更好的反映预报值的精度及可靠性,常作为预测结果评估的主要指标[21,30-31]。因此,基于兰勃特投影,绘制了实验区域内各格网点上每天的RMSE分布图。本文仅给出中纬度区域的分布图,电离层平静期与活跃期的分布图分别如图6与图7所示。

图6 电离层平静期中纬度区域内格网点上的RMSE分布Fig.6 RMSE distribution at grid nodes of the mid-latitude region during the ionospheric quiet period

图7 电离层活跃期中纬度区域内格网点上的RMSE分布Fig.7 RMSE distribution at grid nodes of the mid-latitude region during the ionospheric active period

结合图6和图7可直观地看出,在中纬度地区,本文改进模型的RMSE峰值低于未改进的Prophet框架,且两者均显著优于ARIMA模型。特别是在活跃期第3日的预测中,相比于ARIMA模型,本文改进模型能将RMSE峰值降低约4 TECu。此外,平静期以及活跃期前2日的预报中,本文改进模型的RMSE峰值低于2 TECu,精度较为理想。而在活跃期第三日,RMSE峰值有所增加,约为3 TECu。总的来说,相比其他模型,本文改进模型预报结果的RMSE总体较低,精度较为理想,在实验区域内有良好的适用性,进一步验证了本文改进模型的有效性。

进一步分析3种模型预报残差,并统计了以1 TECu、2 TECu、3 TECu为节点的不同区间内的残差比例,在电离层平静期和活跃期的统计结果分别如表6和表7所示。

表6 电离层平静期不同实验区域内预报残差Δ统计表Table 6 Statistical table of prediction residuals Δ in different experimental areas during the ionosphere quiet period

表7 电离层活跃期不同实验区域内预报残差Δ统计表Table 7 Statistical table of prediction residuals Δ in different experimental areas during the ionosphere active period

为更直观地分析表6与表7的统计结果,对表6与表7中本文改进模型在3天预测时段内的预报残差统计结果进行了整合,绘制了百分比环形图,并在环形图内部重点给出了本文改进模型在3天预测时段内小于3 TECu的残差所占的百分比,如图8所示。

结合表6、表7及图8以看出,电离层活跃期预测时段内,在低纬度地区,本文改进模型3 TECu以内的预报残差百分比优于75%;电离层平静期预测时段内,在低纬度地区3 TECu以内的预报残差百分比优于85%;而无论是在电离层平静期还是活跃期,中、高纬度地区预测时段内的预报残差总体上均在3 TECu以内。从预报残差的角度来看,该结果与IGS本身提供的TEC值精度相当[15]。

图8 本文改进模型3天的总体预报残差Δ统计图Fig.8 Statistical chart of the three-day general prediction residuals Δ calculated by the improved model of this paper

从表6和表7可以看出,3天的预测时段内,本文改进模型在3 TECu以内的预报残差百分比略优于未改进的Prophet框架,而在其他分类区间内互有优劣,而上述两模型的预报残差百分比显著优于ARIMA模型。总体来说,本文改进模型具有较高的预报精度,是一种相对简单且比较理想的预测方法。

对比表6和表7可以看出,活跃期的预报残差大于平静期,且预报残差随纬度降低而增大。其原因在前文中已有详细的分析,简单来说即电离层受复杂因素影响,非平稳性非线性特征增强,导致建模难度增加,偏差增大,严重影响了预报精度。

3 结 论

本文提出了一种小波分解与Prophet框架融合的时间序列预测模型,并在建模中考虑了地磁扰动对电离层的影响,应用于电离层VTEC短期预报。利用IGS发布的GIM格网数据,分别基于电离层平静期数据与活跃期数据进行了实验,通过RMSE、MAE、MAPE 3个性能评估指标对预报结果进行了评估,并从预报残差的角度对预测精度进行了进一步的分析。实验结果表明该模型的预报精度优于未改进的Prophet框架,显著优于以往文献中常采用的ARIMA模型,且在中、高纬度地区表现出良好的适用性,验证了改进模型的预报精度与适用性。

为获取建模所需的先验信息,讨论了磁暴等特殊事件的确定方法,并对电离层活跃期的地磁扰动强度进行了分析。通过研究活跃期时段地磁指数Ap与DST指数的变化可知,磁暴发生时DST指数达到极小值,而Ap指数明显增大。则可根据Ap指数判断某日的地磁扰动是否剧烈,即可获取建模所需的先验信息,并构建特殊事件列表。