旋转相控阵雷达变数据率目标跟踪算法

李纪三,蔡文彬,耿利祥,刘 溶,任 渊

(中国船舶重工集团公司第七二四研究所,江苏 南京 211106)

0 引 言

相控阵雷达在系统反应时间、电子对抗性能、多功能多任务等方面的优势可以很好地满足舰警戒探测系统的需求,已在国内外舰艇上广泛应用[1]。与固定相控阵雷达相比,两维旋转多功能相控阵雷达具有经济性和适装性等优点,为中小舰艇提供了良好的解决方案,如法国泰勒斯雷达NS100即采用两维旋转相控阵体制[2]。

相控阵雷达采用具有波束捷变能力的阵列天线,可执行搜索、目标跟踪、制导等多种任务[3],为充分发挥相控阵雷达作战效能,需要根据当前态势和任务负载情形,基于自适应的策略对资源使用进行优化调度[4]。对相控阵雷达资源调度优化主要涉及3个方向。

(1) 任务冲突消解:若多个异类任务竞争同一时间片资源,在基于任务时间窗和优先级的调度策略约束下，通过各种自适应波束编排算法,使系统在有限时间内执行尽可能多的任务[5-7]。基于任务优先级的调度方法主要包括空闲时间最短最领先、截止期最早最领先、最早放行最领先、可达截止期最早最领先、价值最高最领先、价值密度最大最领先等策略,文献[8]对国内外研究进行了综述。

(2) 搜索资源优化:包括最优波位编排、搜索空域划分和搜索周期设计[9],在保证空域覆盖和对目标发现概率基础上,使搜索消耗时间最少[10]。

(3) 跟踪资源优化:包括目标跟踪数据率和每次跟踪驻留时间,通常数据率高，目标跟踪精度高,跟踪成功率高,但消耗时间资源多；数据率低，时间资源消耗少,目标机动时会跑出波门,对目标重新捕获需要更多时间资源[11]。在保证跟踪稳定度和跟踪精度基础上,需要选择一种优化策略,自适应地确定目标跟踪数据率。1986年,Cohen提出基于跟踪残差的自适应数据率跟踪算法[12]。文献[13]提出了基于协方差偏差均值最小准则和最大协方差偏差最小准则两种资源管理算法。文献[14]提出了一种基于交互多模型(interacting multiple model,IMM)的自适应更新率方法,更新间隔与位置残差的平方根成反比,在更新间隔的计算公式中引入了一个可控参数,用以平衡跟踪精度和系统负载。文献[15]提出了一种自适应更新率跟踪应用框架,引入一种代价函数平衡雷达资源和跟踪误差。文献[16]针对传统自适应采样跟踪间隔只适用单一模型并且采样率稳定性差的问题,提出了一种基于相对机动强度的自适应采样交互多模型算法。文献[17-18]提出一种基于服务质量约束的资源分配方法,应用于相控阵雷达组网中的多目标跟踪。文献[19]在Blackman和Van Keuk研究的基础上，提出一种最优数据率计算方法应用于线性Singer模型上,滤波方法采用Kalman滤波器。文献[20]将自适应算法应用在任意非线性滤波器上,包括扩展卡尔曼,不敏卡尔曼和交互多模型上。文献[21]提出了一种采样周期选择算法,该算法基于随机采样,通过计算每一个候选采样周期的代价函数,选择满足跟踪性能的采样周期里的最大值。文献[22]综合分析了采样周期和驻留时间对跟踪性能的影响,并对时间资源利用遗传算法进行了优化,但是该算法没有考虑目标可能的机动性和复杂的杂波环境。文献[23]综合考虑了固定以及可变检测概率对目标跟踪精度的影响,对雷达的时间参数进行了优化。

以上研究在固定面阵相控阵雷达上取得了很好效果,固定面阵相控阵雷达由3个或4个面阵覆盖360°探测空域组成,电子波束可以实时无惯性照射到威力范围内任一目标,跟踪数据率可依据某种准则连续取值,范围覆盖0.1～20 s。相比固定面阵相控阵雷达，旋转相控阵雷达有其自身特点:① 天线360°旋转,面阵的法线方向能到达任一方位;② 对任一方位,在66.7%左右的天线周期内(假设天线的电扫范围是120°)波束无法覆盖。

旋转相控阵雷达由于天线旋转和波束指向限制,跟踪数据率不能自适应取值。文献[12]中利用残差与归一化的噪声方差比值,确定下一时刻采样周期,采样周期随目标机动自适应减小，为防止无限制增加和减小,采样周期限制在0.25～4 s范围内。仿真算例中在直角坐标系中计算残差,用固定噪声归一化残差,这种方法不适用于旋转相控阵雷达跟踪。在直角坐标系下对残差归一化须在不同的距离段采用不同的噪声值,在实际工程中目标的过程噪声估计困难,而已知的是雷达对目标的测量值(方位、距离和仰角)和测量噪声。文献[12]在直角坐标系下计算的归一化残差在远距离处会比实际偏大,会把噪声的波动误判为目标的机动。本文在文献[12]研究基础上,将基于残差自适应数据率跟踪方法应用到旋转相控阵雷达跟踪加搜索(track and search,TAS)模式中,在直角坐标系下基于α-β滤波器对目标进行状态估计,在球坐标系下计算残差,并用量测噪声对残差进行归一化,利用归一化的残差计算下个采样周期,该方法在保证跟踪精度的前提下,能有效地节省跟踪时间资源。

基于旋转相控阵雷达多任务、多功能的特点,为了充分发挥其能力,本文提出一种基于残差的离散取值变数据率跟踪算法应用到旋转相控阵雷达的目标跟踪中。在文献[12]算法基础上,改变其残差计算的坐标系和归一化方式,避免了原算法过程噪声计算复杂等不足,将其应用到旋转相控阵雷达的跟踪中,提高了跟踪资源的使用效率。

1 旋转相控阵雷达跟踪数据率分析

相控阵雷达天线增益随扫描角增大而变小,大角度扫描角将会导致降低作用距离和增大测量误差,天线扫描角为(φ,θ),其中φ和θ分别是与天线法线方向的方位夹角和仰角夹角,雷达信噪比将由天线法线扫描的SNR0下降到SNRs:

SNRs=SNR0cos2φcos2θ

(1)

当扫描角(φ=60°,θ=60°)时,信噪比将下降法线方向的12 dB。为保证天线增益和测量精度,设定最大扫描角为45°,此时信噪比比法线方向下降6 dB。

如图1所示,旋转相控阵雷达每个天线周期可对目标采样3次:提前45°、天线法线方向,回扫45°。

图1 旋转相控阵雷达偏扫示意图Fig.1 Slanting scan schematic diagram of rotating phased array radar

为从技术层面说明本文算法,不失一般性,假设天线的转速是30 r/min,如图2所示。

图2 变数据率跟踪示意图Fig.2 Varialble date rate tracking diagram

天线周期1可能采样点为A,B,C,天线周期2可能采样点为D,E,F,由于天线旋转和电子波束偏移扫描的限制,目标采样最大间隔在CD之间,方位上相差270°,时间上相差0.75个天线周期,最小的间隔AB,BC,DE,DF之间方位上相差45°,时间上相差250 ms。对于天线周期2的跟踪来说,由于此时目标在天线背面,电子波束无法进行照射,D点的数据更新间隔显著长于E和F点的数据更新间隔,D点相较于E和F点,跟踪误差和失跟风险性明显增加。如果N时刻在A处对目标进行采样,若N时刻的跟踪残差较大,N+1时刻可选择B和C采样点,如果跟踪的残差较小,可在下个天线周期选择D，E，F采样点。由以上分析可知,旋转相控阵雷达的跟踪数据率只能离散取值,可能的离散取值如表1～表3所示。应当注意,当目标机动程度过大,0.25～4 s范围的采样间隔范围就不能满足可靠跟踪,在工程应用时,需要根据跟踪目标的机动性重新计算采样间隔的范围。本文为了和文献[7]进行算法性能对比,故也取相同的采样间隔范围。如果n时刻的扫描是提前45°,即在A或者D点,则n+1时刻的采样点选择如表1所示。如果n时刻的扫描是法线方向,即在B或者E点,则n+1时刻的采样点选择如表2所示。如果n时刻的扫描是回扫45°,即在C或者F点,则n+1时刻的采样点选择如表3所示。

表1 提前45°扫描的采样周期取值Table 1 Sampling period value of scanning 45° in advance

表2 法线方向扫描的采样周期取值Table 2 Sampling period value of scanning in normal direction

表3 回扫45°的采样周期取值Table 3 Sampling period value of scanning after 45°

在每次跟踪滤波后,根据当前的残差计算出下个周期的采样周期,采样周期跟表1～表3中的不一定相符,然后找与表1～表3中最近的值作为下个周期的采样周期。

2 α-β滤波器

常增益α-β滤波器具有计算量小和实现简单等优点,在工程上获得广泛应用,可用以下3个关系式描述[12]:

xp(n)=xs(n-1)+vs(n-1)Ts(n-1)

(2)

xs(n)=xp(n)+α[xm(n)-xp(n)]

(3)

vs(n)=vs(n-1)+β/T(n-1)[xm(n)-xp(n)]

(4)

式中,xp(n)为预测值;xs(n)为滤波值;vs(n)为速度滤波值;α为位置滤波增益;xm(n)为时刻t(n)的位置量测值;β为速度滤波增益；T为采样周期;T(n)为时刻t(n)与t(n+1)间的采样周期,即

T(n)=t(n+1)-t(n)

(5)

残差e(n)定义为t(n)时刻测量值xm(n)与预测值xp(n)之差,即

e(n)=xm(n)-xp(n)

(6)

对于具有均匀采样周期T的α-β滤波器,由恒加速Acons输入所引起的预测位置误差正比于加速度和采样周期的平方:

E=AconsT2/β

(7)

跟踪滤波器的残差随机动目标加速度成比例地增加。

在雷达跟踪中，式(6)中xm(n)无法直接获得,因为雷达测量是在球坐标下完成的(设正北方向为0°,方位顺时针从0°到360°),测量方程在球坐标系下是线性方程,在直角坐标系下是非线性方程。目标运动方程在直角坐标系下可线性描述,需要将量测值转换到直角坐标系中，再利用α-β滤波算法进行处理。

(8)

(9)

(10)

(11)

(12)

用过程噪声标准差σ对残差e(n)进行归一化,则归一化残差为

e0(n)=|e(n)|/σ

(13)

当利用以上算法对残差进行归一化时,如果残差在目标机动时要自适应地保持在一定范围内,则采样周期需要随着目标机动加速度的平方根增大而等比例减小,即反比于归一化残差的平方根,因此可得出采样周期的计算公式为

(14)

文献[12]中采样周期的变化范围限制在最大4 s与最小0.25 s,当归一化残差超过4时,采样周期选择2 s,超过16时,采样周期选择1 s,超过64时,采样周期选择0.5 s。进一步,若归一化残差大于256时,则采样周期选择0.25 s。反过来,如果归一化残差小于1,则采样周期增加(但是不超过设定的最大值4 s)。

3 基于残差变数据跟踪算法

雷达目标跟踪通常依赖于两个方程:一个是目标的运动方程,也称状态方程;另一个是量测方程,描述了量测值与状态矢量之间的函数关系,对目标的运动方程以及量测方程的描述要结合相应的坐标系进行,坐标系的选择直接影响滤波精度和滤波的运算量。

在直角坐标系下,滤波的优点是目标的运动模型描述最佳,但需要把球坐标系下的量测值直接转化成直角坐标系,转换后的量测噪声是非高斯、非线性和状态依赖的,给滤波处理带来了新的困难和复杂度。在球坐标系下，跟踪最大的缺点是目标运动方程推导复杂,且方程高度非线性。因此选择在直角坐标下计算目标的状态预测值,然后将状态预测值和协方差转化到量测坐标系中,从而完成量测坐标系下的状态预测值计算,根据状态预测值和量测值计算出残差,根据残差计算出下个周期的采样间隔。

由式(10)～式(12)可以看出,方差与距离的平方相关且计算复杂,在文献[7]中利用了常量噪声对残差进行归一化,由于仿真的整个航路距离相差不大,可以用常量来近似。如果航路中的点距离相差很大,须按照式(11)～式(13)在不同距离段采用不同的噪声,特别是距离远的地方,目标机动仍跑不出雷达的照射波束宽度内。利用常量噪声归一化对目标的机动判决不准确,违背了变数据率的初衷,如果用式(11)～式(13)实时计算噪声,计算量大且随着目标距离和角度的变化每次都需要重新计算,而雷达的量测噪声是个常数,更适合工程应用。

本文在文献[12]的基础上对算法进行了改进,在直角坐标系下滤波,在量测坐标系下计算残差,利用雷达本身的量测噪声对残差进行归一化[25],步骤如下。

步骤 1对n时刻状态进行预测:

(15)

步骤 2将直角坐标系下的预测值转换为球坐标系:

(16)

步骤 3雷达在(βp(n),θp(n))照射后得到的量测值(rm(n),βm(n),θm(n)),将量测值转为直角坐标系:

(17)

步骤 4在直角坐标系下对n时刻的位置和速度进行滤波:

(18)

(19)

步骤 5根据n时刻的量测值和预测值计算n时刻的残差。根据式(6)可知,残差定义为量测值减去预测值,其表征当前跟踪的好坏程度,量测值是目标的真值加上量测噪声,预测值是目标的真值加上过程噪声(也称机动噪声),因此残差包含机动噪声和量测噪声两部分。在直角坐标系下,如果没有机动,则残差只有量测噪声,用残差和量测噪声的比值来确定目标是否机动,这个过程就是前文提到的归一化。但是，直角坐标系下量测噪声需要根据雷达在球坐标系下的量测值和量测噪声，利用式(10)～式(12)实时近似计算。而在球坐标系下,残差为球坐标系下的量测值减去预测值,量测值是雷达直接读取的,预测值需要将直角坐标系下的预测值转换过来,雷达的量测噪声不随着目标的方位和距离变化,因此球坐标系下残差计算量更小和准确度更优。残差计算如下:

(20)

步骤 6残差归一化:

(21)

步骤 7根据n时刻的残差计算n+1时刻的采样周期:

(22)

步骤 8根据步骤7计算出来的采样周期和当前的采样位置,按照表1～表3找到与T(n)最近的值最作为下一个采样周期。

为了对比验证算法的有效性,参照文献[12]对采样周期设置相同的最大值与最小值,分别为4 s和0.25 s。在工程实际应用时需要根据目标的机动性重新计算采样周期的取值范围,同时为防止目标机动和噪声对残差造成比较大的起伏,从而引起采样周期的剧烈变化,对采样周期进行了平滑设计:当归一化残差在[0.8,1.2]时,保持采样周期不变；大于1.2时，采样周期减少0.25 s;小于0.8时,采样周期增加0.25 s。根据第2节的分析,增加0.25 s可能没有这一档,从表1～表3中选择离计算值最近的数值作为下一个采样周期。例如,当前采样位置是C点,采样周期是0.5 s,计算出来的残差小于0.8,要增加到0.75,但是离C最近的是D采样点,也就是天线转到目标最快也是1.5 s后了,所以下个采样周期为1.5 s。

当残差大于1.2时,要减小采样周期,如果当前采样点是A点,采样周期是1.5 s,归一化残差大于1.2,计算出来采样周期为1.25 s,但是在A对应的下个采样周期没有1.25 s这一档，只有缩小到0.5 s,对应采样位置是C点。

4 仿真实验

为了验证本文所提的基于残差变数据率跟踪算法的有效性,与常规的天线周期作为数据率的定数据率跟踪算法进行了比较,利用100 次蒙特卡罗计算得到的均方根误差(root mean square error,RMSE) 作为滤波性能的衡量标准,对比分析了两种算法在目标作匀速直线运动和加速度为10g圆周转弯机动情况下的跟踪性能。

仿真的雷达参数为:采用与法国泰勒斯NS100体制相同的单面旋转相控阵雷达,天线转速为30 r/min,天线旋转周期为2 s,雷达位于坐标原点(0,0)处,量测精度为距离50 m,方位0.2°,仰角0.2°。

仿真场景为:如图3所示,飞机从方位45°、距离90 km、高度15 km,以速度800 km/h沿直线飞向雷达,匀速直线飞行50 s后开始作圆周转弯机动,转弯向心加速度为10g、转弯半径为6.8 km,转弯90°后沿着直线以速度800 km/h远离雷达飞行60 s结束。

图3 目标飞行轨迹Fig.3 Target flight trajectory

雷达真值和量测的产生:在直角坐标系下,按照直线运动方程和圆周运动方程以时间间隔0.01 s生成每个时刻的飞机航迹真值数据(x(n),y(n),z(n))。利用式(23),将直角坐标系下的真值数据转换为球坐标系下的真值数据(r(n),β(n),θ(n)),将球坐标系下的真值数据叠加上雷达的量测噪声,产生了每个时刻的雷达量测值(rm(n),βm(n),θm(n))。

(23)

仿真结果:目标机动主要发生在方位上,因此主要关注方位跟踪残差和精度,进行了两组仿真,第一组是常规的两秒数据率,雷达只在法线方向附近对目标进行采样；第二组利用第4节中自适应数据率算法进行跟踪。

按照式(6)计算了两种算法的残差,如图4所示。残差的最大值影响跟踪的稳定性,由式(6)可看出，残差是预测值减去量测值得到,因为是在预测点对目标进行照射,如果目标的真实位置离预测点超过照射波束的半波宽,则无法照射到目标。

图4 跟踪残差对比Fig.4 Comparison of tracking residuals

从图4可以看出,常规算法跟踪残差最大达到3°,因此需要宽波束照射才能保证目标的不失跟,而变数据率最大残差只有1°,只需要窄波束就能罩住目标。如果采用相同宽度的波束,变数据率算法比常规算法对机动目标跟踪的稳定性更强,从这个角度讲,变数据率算法提高了跟踪成功率。

对两种算法的跟踪精度进行对比,精度的评估采用RMSE计算:

(24)

式中，M是蒙特卡罗仿真次数；k是采样点的序数。

方位RMSE的跟踪结果如图5所示,采用定数据率2 s(与天线的周期相同)跟踪，在直线运动阶段保持在0.2°以内,在机动转弯阶段达到0.9°。变数据率跟踪在直线运动阶段保持0.2°左右,在转弯阶段达到最大值0.5°。图6可以看出,两种方法在仰角的跟踪精度要高于相应方位的跟踪精度,这是由于目标是在方位进行机动。图7是距离的RMSE,精度的变化趋势和方位仰角相同,在机动阶段跟踪精度明显下降。

图5 方位RMSE对比Fig.5 Comparison of azimuth RMSE

图6 仰角RMSE对比Fig.6 Comparison of elevation RMSE

图7 距离RMSE对比Fig.7 Comparison of distance RMSE

图5～图7的结果表明,目标机动发生后，本文算法的最大跟踪误差减小,但在非机动跟踪阶段的方位、仰角、距离误差均大于传统算法,这是因为目标跟踪误差与跟踪数据率和滤波算法息息相关。本文采用与传统算法相同的滤波算法,但是数据率采用了不同的策略,在目标机动辨识的基础上,目标机动阶段采用高数据率,而在其他情况下采用较低数据率。目标在满足一定跟踪精度下,优化雷达资源使用。

利用方位的量测噪声0.3°和式(14),对图4方位残差归一化后开根号,根据式(23)确定每个时刻的采样周期,某次跟踪的每个时刻的数据率(数据率设置为与天线转速,即天线每转一圈需要的时间一致)如图8所示。

图8 目标跟踪数据率Fig.8 Target tracking date rate

从图8可以看出,目标在直线运动阶段的采样周期高于机动时刻的采样周期。从时刻60 s开始,采样周期从3.5 s开始下降,每次采样周期减少0.25 s,得出了期望的值。根据目标和雷达的相对位置,从表1～表3中查找到了可以选用的采样周期,依次为3.5-2.5-2-0.25。在目标的转弯时刻,采样周期一直在0.5 s和1.5 s之间转换,此时相当于一个天线周期对目标采样两次,提前45°采样一次,然后回扫45°采样一次,目标沿着直线飞离雷达时,采样周期又下降到了4 s。如果目标的机动性再增加,就需要在一个天线周期内采样3次,及采样周期为0.25-1.5-0.25-0.25-1.5的数据对目标进行跟踪。

进行300次蒙特卡罗仿真,利用式(25)计算采样周期平均值,统计结果如图9所示。

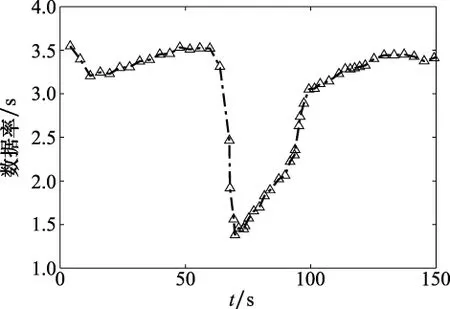
图9 平均数据率Fig.9 Average date rate

(25)

(26)

利用式(26)计算得到整个航路平均采样周期为2.44 s。在匀速直线运动阶段,跟踪精度与定数据率2 s的常规算法相当,变数据率跟踪的平均周期为3.3 s,满足跟踪的精度要求,时间资源节省39%。在机动阶段,变数据率跟踪的平均周期为1 s(0.5 s和1.5 s交替,一圈内跟踪两次),跟踪时间资源比常规算法多了50%,跟踪精度提高了44.4%。从整个航路来说,变数据率的平均采样周期为2.44 s,相对于常规算法时间节省了22%。

5 结 论

本文在Cohen的研究基础上,提出了一种基于残差变采样周期的跟踪算法并应用到旋转相控阵雷达的跟踪中。该算法将残差计算从直角坐标转换到球坐标系,并用量测噪声代替过程噪声对残差进行归一化。根据采样位置和天线的偏移限制利用归一化残差计算出了下一时刻的采样周期。仿真结果表明,相对于常规的与天线周期相同数据率的跟踪算法,在匀速直线运动时能够在保证精度的前提下自适应增大采样周期,在目标机动时自适应减小采样间隔,增加了对机动目标的跟踪稳定性,达到了对跟踪资源优化调度的目标。

此外,为满足日益复杂电磁环境下的探测需求,对多功能雷达跟踪资源调度也提出许多新的要求,下一步的研究工作需将环境复杂性导致的量测不确定性考虑进来,在重杂波区或者电磁干扰情况下,可能导致雷达检测概率降低造成目标单次采样失跟(波门内目标回波没过检测门限)的情况,因此自适应采样周期的计算要将检测概率的影响纳入进来。