无环境信息下多尺度网格细胞群空间表征模型

赵辰豪,吴德伟,韩 昆,代传金

(空军工程大学信息与导航学院,陕西 西安 710077)

0 引 言

导航是检测和控制运行体从一个地方移动到另一个地方的过程[1]。随着导航智能化的发展,自主导航技术[2]逐渐成为导航研究热点。自主导航最初是指不借助人工设置的目标和信息源的导航仪器来完成导航的方法[3],如惯性导航[4]、天文导航[5]、仪器导航等。近年来,网格细胞[6]、位置细胞[7]、头朝向细胞[8]、速度细胞[9]、边界细胞[10]等大脑导航细胞的发现,使大脑空间导航机制[11]理论逐渐成熟。大脑导航系统为研究自主导航技术提供了一种新的思路。脑神经科学与导航的结合产生一种新的新型仿生智能自主导航技术——类脑认知导航[12],其通过模仿大脑,建立具有自主性、智能化的导航机制[13]。实现类脑认知导航首先要解决的问题是如何构建认知图[14],而认知图的构建方式是由环境信息决定的。在无环境信息下,需要建立符合类脑机制的空间表征;部分或充足环境下,需要将已知的信息转化为能够被运行体获取的类脑表征信息。

目前,关于认知图构建的研究还处于初始阶段,主要集中在无环境信息下的空间表征[13]。无环境信息下的空间表征是利用网格细胞模型生成特殊形式的“坐标系统”,对空间进行标定[15]。网格细胞的模型主要有振荡干涉模型[16]与吸引子网络模型[17-19]。Tsodyks根据网格细胞空间六边形放电域和周期放电等特性,提出吸引子网络模型,模拟网格细胞的性能[20]。Burak针对吸引子网络无法整合速度信息与网络规模小等问题,建立能整合速度信息的吸引子网络模型,并成功在10～100 m范围内保持速度整合的准确性[21]。于乃功等基于此模型对空间进行表征,但传统吸引子网络只能感应物体运行的合速度,网格细胞的放电状态只对应已运行的位置,无法表征未探索的位置,探索路径的设置十分复杂,对位置环境的探索效率过低[22]。文献[23]通过记录网格细胞的周期性放电率规律,提出一种基于单一尺度的网格细胞表征空间的方法,并在一定范围内证明了表征模型的有效性,但单一尺度网格细胞表征空间受到最大网格间距的限制,表征范围有限。Edvardsen基于多放电野间距的网格细胞连续吸引子网络模型实现了空间表征并完成目标导向导航,方向信息和距离信息由多个方向的矢量累加提供,但是导航范围仅限于最大网格细胞放电野间距[24]。针对表征范围的问题,文献[25]提出多尺度网格细胞模型,并基于该模型建立空间表征,实验结果证明多尺度模型能有效扩大表征范围,但文中仅以单个网格细胞的放电率周期作为整个网络的周期,存在较大的偶然误差,使得表征结果不准确,表征效果较差。

针对上述问题,本文提出一种多尺度网格细胞群的空间表征模型,并记录网格细胞群的放电状态对空间进行表征。通过减少网格细胞的偏好朝向,生成具有特定感应方向的网格细胞,并进行仿真验证改进后模型的性能。同时，基于改进的模型,选取适当的网格间距比生成多尺度网格细胞,来扩大表征范围,记录整个网格细胞群的放电状态,并通过线性前瞻的方法验证多尺度网格细胞表征一维、二维空间的能力。

1 模 型

本文采用单层网格细胞的连续吸引子网络模型,通过改进该模型速度的感应能力,产生能够响应特定方向的吸引子网络的网格细胞模型。

1.1 网格细胞的吸引子网络模型

假设网格细胞排列于2-D平面上,总数是N=n×n,xi表示网格细胞i的位置。xi的取值范围是(-n/2,-n/2)到(n/2,n/2)。网格细胞i的偏好朝向由θi决定。吸引子网络中网格细胞放电率的计算方法[21]为

(1)

式中,f(·)为线性整流函数,当x>0,f(x)=x;当x≤0,f(x)=0;τ为时间常数;si表示第i个神经元的放电率大小;Wi j为第i个神经元与第j个神经元之间的连接权值;Bi表示第i个网格细胞的前馈输入。

网格权重的表达式[21]为

(2)

W0(x)=a1exp(-γ|x|2)-a2exp(-β|x|2)

(3)

网格细胞前馈输入的表达式[21]为

(4)

式中,α与式(2)中的l为常数,当α≠0且l≠0时,运动速度v与吸引子网络的更新动态的速度相关。网格细胞的前馈输入决定了速度对网格细胞放电状态的影响。A(xi)为包络函数,该函数决定了网格细胞的周期性;本文采用周期性网格细胞,取A(xi)=1。

基于上述过程,能产生一定网格间距的网格细胞。通过设置单个网格细胞的偏好朝向,使该模型能准确响应运行体运动的速度。

1.2 改进的吸引子网络模型

网格细胞输出权重的转移方向和输入速度的方向是由吸引子网络中单个网格细胞的偏好朝向决定的。文献[21]对模型中网格细胞赋予4个不同的偏好朝向,使得网格细胞群只响应运行体的合速度,而不能响应不同方向上的分速度。为了生成具有不同感应方向的网格细胞模型,需要消除网格细胞不同方向之间的关联性。本文对网格细胞模型进行改进,将模型中的偏好朝向减少为两个,设置每4个网格细胞中同时包含两个偏好朝向,并且左右相邻位置与对角线上的网格细胞的偏好朝向不同,即相邻的4个网格细胞的偏好朝向为

(5)

当且仅当θ1-θ2=π时,网格细胞仅感应特定方向速度,不受其他方向速度分量输入的影响。

如图1所示,结合二维空间表征机制,需要设置偏好朝向分别为φ1、φ2的两组网格细胞,同时该偏好朝向对应的方向向量aφ1,aφ2线性无关,即

k1aφ1+k2aφ2≠0,k1≠0；k2≠0

(6)

图1 二维平面的表征Fig.1 Representation of 2-D plane

本文取φ1=0(θ1=0,θ2=π)对应表征水平方向,φ2=π/2(θ1=π/2,θ2=3π/2)对应表征竖直方向。

1.3 多尺度网格细胞群模型

通过调整吸引子网络模型中参数β可得不同间距的网格细胞群,即多尺度网格细胞群模型。假设模型中网格细胞数量为N1×N2,其中N1表示网格细胞群的层数,且同层网格细胞具有相同的尺度。N2=n×n表示单层网格细胞的总数;每一层的网格细胞都能够独立响应运行体的运行速度与方向。

运行体在t时刻的放电率用St表示:

(7)

(8)

通过选择适当的网格间距进行组合,理论上网格细胞放电率向量St的周期能够趋于无穷大。因此,放电率向量St能够与位置一一对应,满足表征空间的条件。但由于放电率维数过大,直接比较向量将变得十分复杂且低效。为提高比较效率,本文采用放电率夹角的计算方法,定义:

(9)

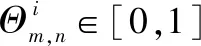
1.4 空间表征及表征效果检验方法

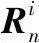
图2 网格细胞空间表征Fig.2 Spatial representation of grid cell

由图2可知,基于多尺度网格细胞群的空间表征的过程可分为5个步骤:

步骤 1设置合理的空间探索方式,并感知运行体的运行速度;

步骤 5重复步骤2～步骤4直至t>Texp,探索结束。

探索结束后需要对生成的表征结果进行分析,检验表征效果的好坏。本文采用空间线性前瞻的方法对网格细胞空间表征结果进行检验。线性前瞻是指运行体保持位置固定,通过向网格细胞输入联想速度,改变网格细胞的放电率。检验表征结果的具体过程如下:

步骤 1给定起点后,对网格细胞群放电率进行赋值。

步骤 2通过向网格细胞模型中输入联想速度,更新网格细胞群的放电率。

步骤 3根据式(8)实时计算当前时刻网格细胞群向量与目标向量的夹角;当该方向的夹角都大于设置的放电阈值h时,停止线性前瞻,直至每层网格细胞的前瞻结束,分别记录各自的停止时间t。

步骤 4计算各个方向上运行的距离,并进行矢量叠加,最终得到网格细胞表征下的起点到目标点的距离与方向。

2 仿真实验与分析

仿真实验对改进后网格细胞模型的性能与多尺度网格细胞群的空间表征能力进行验证。吸引子网络模型的基本参数设置:a1=a2=1,β=3/λ2,γ=1.1β,τ=10 ms,α=0.103 15,l=2,dt=0.5 ms,根据式(2)生成不同感应方向与不同网格间距的权值矩阵W。

2.1 改进网格细胞模型的性能

改进后网格细胞模型的性能验证分为3个部分。首先,验证模型空间六边形的放电样式与网格间距的可调整性;其次,验证网格细胞模型具有特定的感应方向;最后,验证模型整合速度的能力。

设网格细胞模型参数为λ1=13、λ2=20、λ3=26;单层网格细胞个数N2=128×128,图3为λ取不同值时,生成网格细胞的放电样式,其中颜色柱表示网格细胞放电率大小,单位为Hz。设λ=13,单层网格细胞个数N2=50×50,选取感应水平方向的网格细胞,θ1=0,θ2=π;感应竖直方向的网格细胞,θ1=π/2,θ2=3π/2,分别生成感应水平方向的网格细胞与感应竖直方向的网格细胞。

图4和图5分别表示水平速度和竖直速度对不同感应方向上网格细胞放电活动的影响,其中横、纵坐标均为网格细胞个数,颜色柱表示细胞放电率的大小,单位为Hz。由图4和图5可知,当输入速度只存在水平分量时,感应水平方向的网格细胞能够水平运动,而感应竖直方向的网格细胞的状态不发生变化;当输入速度只存在竖直分量时,感应竖直方向的网格细胞能够沿竖直方向运动,感应水平方向的网格细胞的状态保持不变。由此可得,改进后的模型只响应其感应方向上的速度输入,具有特定感应方向。

图3 多尺度网格细胞模型Fig.3 Multi-scale grid cell model

图4 感知水平速度的网格细胞Fig.4 Grid cell perceiving horizontal velocity

图5 感知竖直速度的网格细胞Fig.5 Grid cell perceiving vertical velocity

理论上,网格细胞状态周期与速度成反比,因此可以通过观察速度变化对周期的影响来验证改进模型整合速度的能力。设初始位置处网格细胞放电率向量S=S0,并将此放电率作为参考放电率Sref,然后输入速度对放电率St进行更新,根据式(8)计算参考放电率向量与联想放电率向量之间的夹角Θ。由夹角Θ性质可知,Θ=1时,网格细胞放电率向量为St=S0。因此,峰峰值时间间隔等于完整的网格细胞放电率周期。设模型参数λ1=16、λ2=24,输入速度v1=0.5 m/s、v2=1.0 m/s,图6与图7分别表示将水平网格细胞与竖直网格细胞整合速度的结果。

图6 水平网格细胞模型速度整合结果Fig.6 Velocity integration result of horizontal grid cell model

由图6可知,λ=16时,速度v=0.5 m/s和v=1.0 m/s对应的峰峰值平均时间间隔分别是13.4 s和6.70 s。λ=24时,分别是14.6 s和7.35 s。由图7可得,λ=16时,速度v=0.5 m/s、v=1.0 m/s对应的峰峰值平均时间间隔分别是13.7 s和6.75 s;λ=24时,分别是14.6 s和7.35 s。实验结果表明,当输入的速度增加一倍,峰峰值时间间隔缩小为原来的二分之一,即网格细胞周期变为原来二分之一。因此,改进后的网格细胞模型仍然可以准确的整合速度信息。

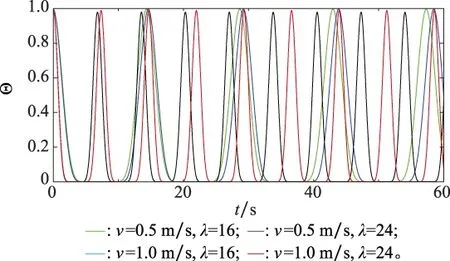
图7 竖直网格细胞模型速度整合结果Fig.7 Velocity integration result of vertical grid cell model

综上所述,改进后的吸引子网络模型能形成稳定的六边形放电域,网格细胞的间距具有可调性,并且模型能够准确地整合速度信息,改变网格细胞的偏好朝向,使吸引子网络模型具有特定的感应方向。

2.2 空间表征及表征结果分析

本实验主要验证空间表征模型对一维空间与二维空间的表征能力,采用线性前瞻的方法对空间的表征结果进行检验。

设单层网格细胞个数N2=50×50,λ1=10、λ2=16、λ3=24,放电率夹角阈值h=0.95。如图8所示,运行体从O点出发,速度v=0.5 m/s,探索并表征一维空间,探索完毕后,运行体以不同路径在已探索空间中运行。路径1为由O点出发,沿直线向红色区域运动。路径2为由O′点出发,沿直线向红色区域运动。路径3为由O点出发,进行变速运动并先后3次经过红色区域。

图8 运行体探索空间的路径Fig.8 Path of exploration

设S=Sred为网格细胞群的目标放电率,图9～图11分别表示沿不同路径运动,放电率向量夹角Θ随时间变化的过程。

图9 沿路径1运行Θ的变化Fig.9 Θ’s change along the path 1

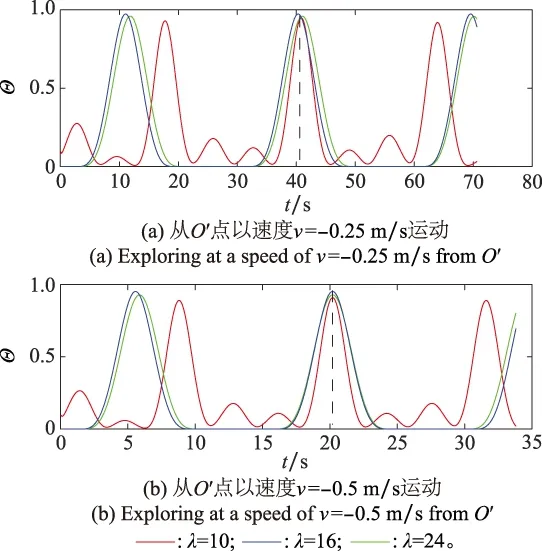
图10 沿路径2运行Θ的变化Fig.10 Θ’s change along the path 2

图11 沿路径3运行Θ的变化Fig.11 Θ’s change along the path 3

如图12所示,待探索空间的大小为100 m×100 m,运行体以匀速的方式从一个顶点沿对角线运行至另一个顶点对空间进行探索,探索过程中运行速度为0.7 m/s,总运行时间为200 s,探索完毕后,共生成300个放电率向量群Si,且Si=[Shor(m),Sver(n)]其中,Shor表示水平方向放电率向量,Shor表示竖直方向放电率向量,m,n∈[0,300]。放电率向量群Si即为二维空间的网格细胞表征。选取不同间距与不同感应方向构建多尺度网格细胞,设单层网格细胞个数N2=50×50,网格细胞模型的参数设置为:λ1=18、λ2=20、λ3=22、λ4=24。采用线性前瞻的过程检验网格细胞表征空间的结果,放电率夹角阈值h=0.95,并分析空间表征性能。

图12 二维空间的探索路径Fig.12 Exploration path of 2-D space

图13为采用传统吸引子网络探索二维空间环境后,使用线性前瞻机制进行检验的结果。由于传统网格细胞模型的限制,运行体只表征已探索的空间,因此运行体仅可以完成由已探索位置到已探索位置的线性前瞻过程。而当起始点或目标点中包含未探索位置时,由于缺乏位置的表征信息,无法开始线性前瞻过程,即该模型未生成关于未探索区域的表征信息。

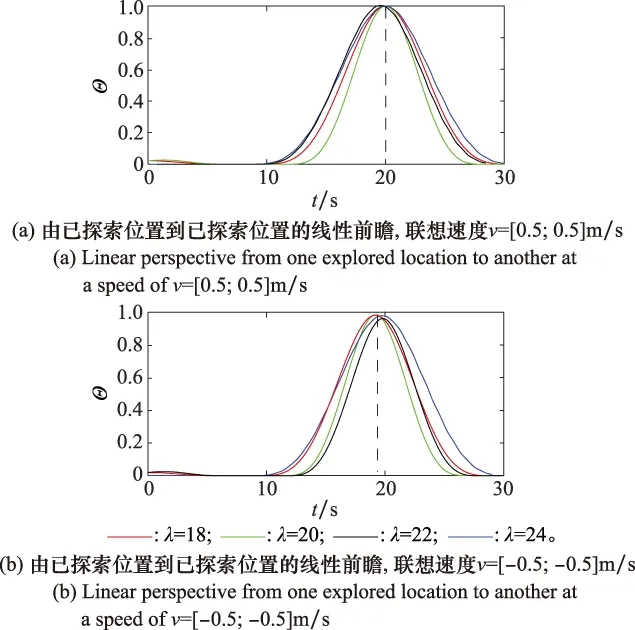
图13 多尺度吸引子网络模型的空间表征Fig.13 Spatial representation of multi-scale attractor network model

图14为采用线性前瞻的方式检验改进后模型表征空间的结果,图中横坐标为线性前瞻的时间,纵坐标为放电率向量夹角的余弦值。图14(a)为运行体由已探索位置导航到已探索位置线性前瞻的过程,设初始状态m=40,目标状态n=60,联想速度v=[0.5;0.5]m/s;出发点至目标点向量为10x+10y,由模型生成的向量为10.11x+10.12y。图14(b)为运行体由已探索位置到未探索位置线性前瞻的过程,设初始状态m=50,目标状态n=30,n1=40,联想速度v=[-0.5;-0.25]m/s;出发点至目标点向量为-10x-5y,由模型生成的向量为-10.10x-5.09y。图14(c)为从未探索的位置导航到探索位置,设初始状态m=30,m1=80,目标状态n=55,n1=55,联想速度v=[0.5;-0.5]m/s;出发点至目标点向量为12.5x-12.5y,由模型生成的向量为12.62x-12.51y。图14(d)为从未探索位置导航到未探索位置,设初始位置m=50,m1=30,目标状态n=30,n1=50,联想速度v=[-0.5;0.5]m/s;出发点至目标点向量为-10x+10y,由模型生成的向量-10.13x+10.06y。

图14 改进后网格细胞模型的空间表征Fig.14 Spatial representation by improved grid cell model

由图13可知,传统吸引子网络模型只能感知运行体运动的合速度,因此仅可以表征探索路径上的位置,对于未经历过的位置无法表征。由图14可知,改进后的模型具有特定的感应方向,除表征探索路径上的位置外,还能表征空间中未探索的位置,极大地缩短了探索时间,提高空间的表征能力。

由图15可知,已探索位置与未探索位置的误差都保持在0.2 m以内。本文中的位置误差主要取决于构建空间表征时,储存放电率向量的时间间隔tΔ。仿真实验中时间间隔设置tΔ=0.2 s,运行体运动速度约为1 m/s,因此放电率向量之间距离间隔不超过0.2 m,所以误差基本保持在0.2 m以内。

图15 表征结果中各位置的距离误差Fig.15 Distance error of each position in the representation

图16表示不同时间间隔tΔ,探索速度为1 m/s,空间表征结果的误差大小。由图可知,在表征不同大小的空间时,设置合理的时间间隔,存储放电率向量,使结果的精度满足空间表征要求。

图16 不同时间间隔各位置的距离误差Fig.16 Distance error of each position at different tΔ

综上可知,通过多尺度网格细胞群生成的网格细胞放电率向量,满足表征一维空间、二维空间的需求。调节放电率向量存储的时间间隔,可以调整误差的大小,以满足不同表征需求。

3 结 论

本文主要解决了无环境信息下,采用多尺度网格细胞群模型表征空间的问题。通过改进传统吸引子模型,生成具有特定感应方向的网格细胞模型。通过仿真实验验证了改进后模型的有效性,检验了模型一维、二维空间的表征能力。但在有环境信息下的空间表征除了网格细胞对空间进行标定外,还需采用位置细胞等对标志物等位置进行记忆。因此,进一步实现无环境信息下的空间表征,需要结合位置细胞进行更深的研究。