修正钟差的脉冲星方位误差估计算法

肖永强,王宏力,冯 磊,由四海,何贻洋,许 强

(1.火箭军工程大学导弹工程学院,陕西 西安 710025;2.青州高新技术研究所测试控制系,山东 青州 262500)

0 引 言

X射线脉冲星导航是一种新兴的自主导航方式,其利用脉冲星辐射的信号对航天器进行定位、授时等服务。其自主性强、可靠性高,有望摆脱航天器对全球定位系统(global positioning system,GPS)等卫星导航的依赖,在民用和军事领域有着巨大的发展前景[1-10]。但是目前要将其真正应用到实际工程中仍存在很大的差距,其中一个很重要的原因就是脉冲星方位误差的影响[11-16]。

在脉冲星导航过程中,0.001″的脉冲星方位误差会造成几百米的定位误差[17]。因此,为了提高脉冲星方位误差估计精度,国内学者采用了基于信标卫星的估计[18]、鲁棒滤波估计[19-21]、组合导航[22-24]等方法对脉冲星方位误差进行估计。此外,许强在利用信标卫星进行估计时考虑了实际存在的卫星位置误差的影响[25]。但是上述研究都没有考虑航天器的时钟钟差影响。虽然孙守明等研究了脉冲星导航以及脉冲星与惯性、多普勒等组合导航中的钟差修正[26-28]问题,但是在利用信标卫星进行脉冲星方位误差估计时,依然会受到时钟钟差的影响。然而从目前公开的文献来看,利用信标卫星进行脉冲星方位误差估计中的钟差修正问题尚未有学者研究。当利用信标卫星进行脉冲星方位误差估计时,由于航天器长时间运行,时钟会发生漂移,进而会造成系统偏差,从而使脉冲星方位误差估计精度降低。

为了解决脉冲星方位误差估计时的钟差影响,本文通过分析得出时钟钟差对脉冲星方位误差估计的影响为缓变的过程,可看作系统偏差,常用的处理方式是利用增广状态法。但是若利用增广状态法处理,当系统状态与系统偏差维数相近时,会使滤波计算量增加,且易出现数值不稳定的问题[29]。因此,为了解决上述问题,本文提出了一种考虑钟差修正的两步卡尔曼滤波(two-stage Kalman filter,TSKF)算法。

1 脉冲星方位误差估计原理

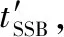
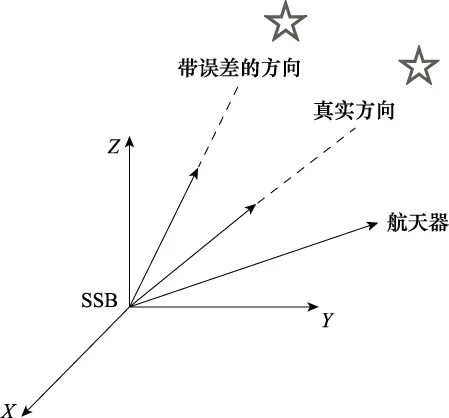
图1 脉冲星方位误差估计原理Fig.1 Principle of pulsar position error estimation

转换过程[1]为

(1)

(2)

式中,tsat为脉冲到达航天器的真实时间;n为真实的脉冲星单位方向矢量。设脉冲星的赤经为α,赤纬为β,则满足:

(3)

设(Δα,Δβ)为脉冲星方位误差,则真实的脉冲星方位与带误差的脉冲星方位满足

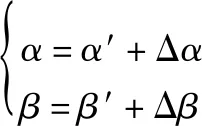
(4)

将式(4)代入式(3),进行泰勒展开并忽略二阶及以上小项可得

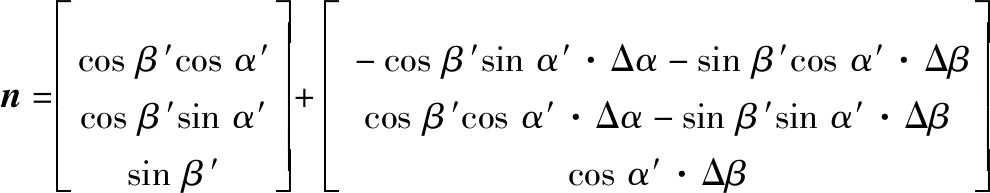
(5)

式中,带误差的脉冲星方向矢量为

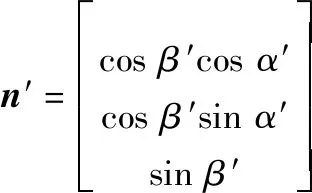
(6)

记脉冲星单位方向矢量误差Δn为

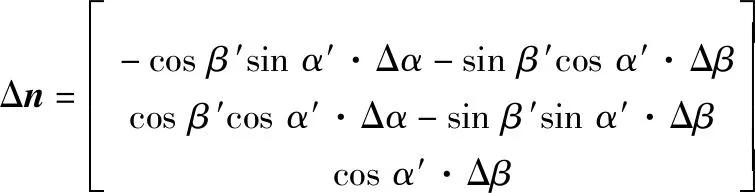
(7)

则可以将式(5)表示为

n-Δn=n′

(8)

(9)

取状态变量为X=[ΔαΔβ]T,则传统脉冲星方位误差估计算法的状态方程和观测方程为

(10)

(11)

式中,状态转移矩阵为

观测矩阵为

式中，Wk和ηk为系统噪声和量测噪声。

2 时钟钟差影响分析

由于航天器时钟频率和相位的漂移,脉冲到达航天器的真实时间和航天器时钟测得的脉冲到达航天器的时间之间存在时钟钟差,设航天器的时钟钟差为δt,则满足

(12)

时钟钟差可通过估计相对于标准时间的钟差、钟差漂移率和钟差漂移率的变化率获得,因此可将卫星时钟钟差模型[30]表示为

(13)

式中,x1、x2和x3分别为钟差、钟差漂移率和钟差漂移率变化率;τ为时间间隔。取状态变量为x=[x1，x2，x3]T,则钟差离散过程模型可表示为

(14)

式中,状态转移矩阵为

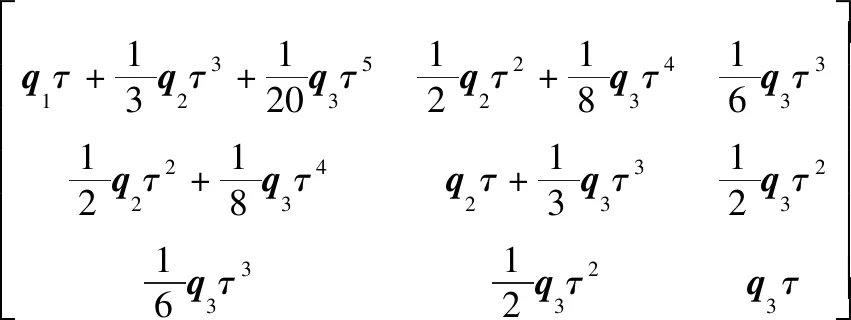
(15)

式中,q1、q2和q3为噪声的功率谱密度。

仿真取时钟误差漂移率为3.637 979×10-12,时钟漂移率的变化率为6.66×10-18/s;根据铷原子钟模型[26],取时钟的噪声谱密度分别为q1=1.11×10-22s,q2=2.22×10-32/s和q3=6.66×10-45/s3。给定时钟初始时刻的钟差为0,取时间间隔为1 s,则可得到钟差随时间的变化如图2所示。

图2 钟差随时间的变化Fig.2 Change of clock error with time

由图2可得,虽然钟差漂移较小,但随着航天器的长时间运行,钟差接近5×10-6s,该值与光速相乘理论上会引起1 500 s左右的定位误差,将会对量测方程式(11)造成较大的影响,进而会对脉冲星方位误差估计造成严重的影响。

使用传统脉冲星方位误差估计算法进行仿真,分别验证其在有无钟差影响下的估计效果。以脉冲星B0531+21作为观测脉冲星,其参数如表1所示。

表1 脉冲星B0531+21参数Table 1 Parameters of pulsar B0531+21

其中,P为脉冲周期,W为脉冲宽度,Fx为脉冲辐射光子流量,pf为一个脉冲周期内脉冲辐射流量与平均辐射流量之比。

脉冲星的观测噪声方差[2]为

(16)

式中,A为探测器有效面积,本仿真中设为1 m2;Bx=0.005 ph·cm-2·s-1,为宇宙背景噪声;d为脉冲宽度W与脉冲周期P之比;tobs为观测时间,设为1 000 s;则可计算[25]得到σ=(77.69 m)2。脉冲星方位误差设为(2 mas,2 mas),初始状态设为0。

使用同一颗卫星,分别在有无钟差影响的情况下进行仿真,卫星轨道参数如表2所示,仿真结果如图3所示。

表2 卫星轨道参数Table 2 Parameters of orbit

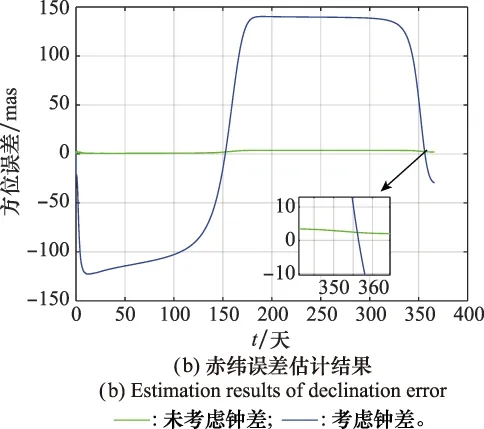
图3 有无钟差的脉冲星方位误差估计结果Fig.3 Estimation results of pulsar position error without correction of clock error

对比分析图3可得,当无钟差影响时,传统脉冲星方位误差估计算法能较为精确地估计方位误差。但当存在钟差时,估计结果误差较大,尤其是赤纬误差,接近80 mas;而且赤经和赤纬误差估计结果都没有收敛到一个定值。可见,时钟钟差会对脉冲星方位误差估计精度产生较大的影响,因此非常有必要对航天器时钟钟差进行修正。

3 修正钟差的脉冲星方位误差估计算法

当考虑钟差时,将式(1)和式(2)相减可得新的观测模型为

(17)

由第1.2节分析可知,钟差变化是一个缓慢过程,常用的处理方法是增广状态法,即将系统状态和钟差组合为新的状态变量进行滤波解算。但是这样就会使系统状态由2维变为5维,不仅会增加运算负担,还容易造成数值不稳定的问题[29]。因此,为了解决上述问题,本文采用TSKF算法。

TSKF算法是由Friedland提出用于处理系统常值偏差问题[31],Ignagni 在这基础上将其应用到处理缓变偏差上[32]。该算法解耦状态估计与系统偏差估计,可有效减小滤波过程中的计算量,提高数值计算稳定性。王奕迪等在前期研究中也将其应用到了脉冲星导航中[33-34]。

根据TSKF算法原理取第一步滤波的状态量为X=[Δα,Δβ]T,第二步滤波状态量b为钟差δt,可将方位误差估计的TSKF算法方程写为

一步滤波方程:

Xk/k-1=AkXk-1

(18)

(19)

(20)

Xk=Xk/k-1+Kk(Zk-HkXk/k-1)

(21)

Pk=(I-KkHk)Pk/k-1

(22)

二步滤波方程:

Uk=Ak-1Vk-1+Bk-1

(23)

Sk=HkUk+Ck

(24)

(25)

Vk=Uk-KkSk

(26)

(27)

(28)

最终估计结果为

(29)

式中,Qk为系统噪声Wk的方差;Pk为状态量的协方差;Rk为观测噪声ηk的方差;Bk为δt在式(11)中的驱动方程;Ck为δt在观测方程(12)中的驱动方程。由上述分析可得,Bk=0,Ck=c·Φ。

仿真条件同第2节,估计结果如图4所示。

图4 TSKF算法估计结果Fig.4 Estimation results of TSKF algorithm

为了进一步验证所提算法的有效性,选取不同的钟差对比传统算法与本文所提算法的估计结果,如表3所示。

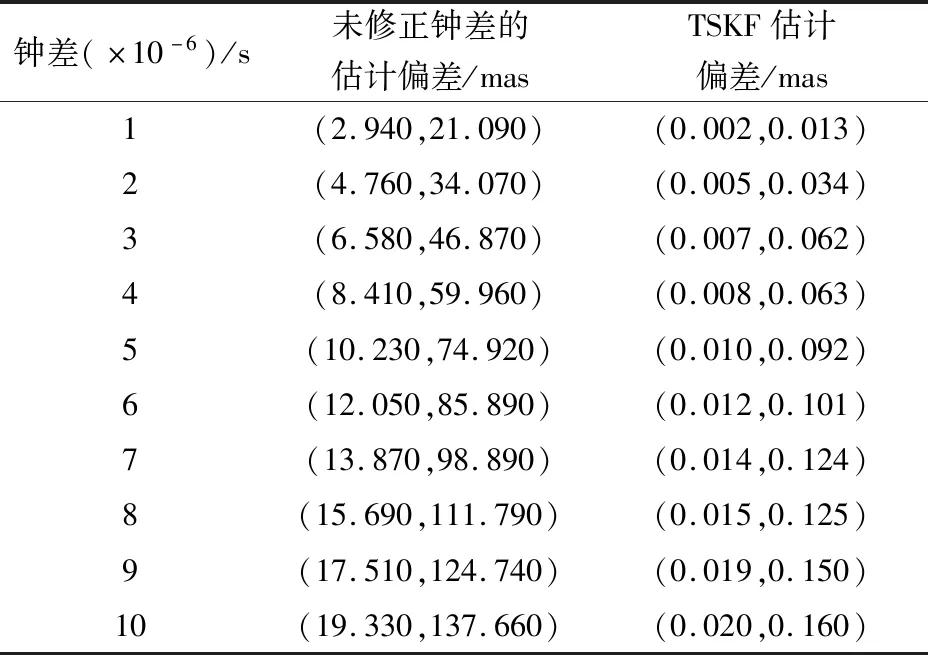
表3 不同钟差条件下TSKF算法估计偏差Table 3 TSKF estimation bias under different clock errors

由图4和表3可得,当不考虑钟差的传统算法估计偏差较大时,本文所提出的考虑钟差的TSKF算法估计精度较高,赤经和赤纬误差估计精度均能保持在0.1 mas以内,且都能收敛到2 mas左右。可见本文所提算法能有效隔离时钟钟差的影响,使估计精度保持在无钟差影响下的水平。

为比较TSKF与增广状态滤波算法(augmented state Kalman filter algorithm,ASKF)的精度,仿真条件同第2节,得到仿真结果如图5所示。由图5可得,在10～50天内,TSKF赤经估计结果振幅略高于ASKF,二者都能很快收敛到2 mas左右,最终估计结果精度相当,均在0.01 mas以内。0～50天,TSKF赤纬估计结果偏差大于ASKF,但处于可控范围内,且TSKF收敛速度略快于ASKF,最终估计结果TSKF精度略低于ASKF,但偏差在0.06 mas以内,仍在可控范围内。其他条件不变,对比两种算法在不同钟差条件下的估计结果,如表4所示。表4也验证了TSKF算法估计结果接近ASKF,使方位误差估计精度保持在较高的水平。为比较两者的计算量,统计上述仿真实验中两种算法Matlab程序中的浮点计算次数,得到TSKF算法133 480 860次,ASKF算法316 957 544次,可得TSKF运算量远小于ASKF,运算量减小了57.89%,有效地减小了计算负担。

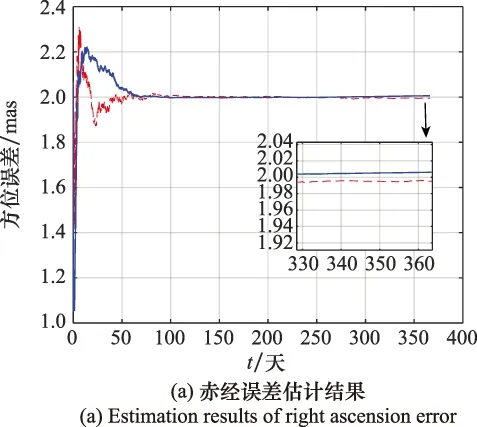
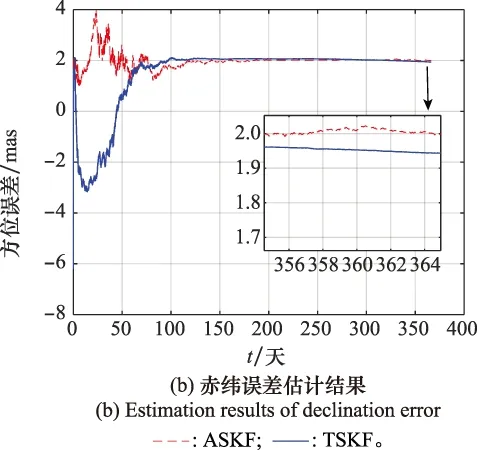
图5 两种算法估计结果对比Fig.5 Estimated results comparison of two algorithms

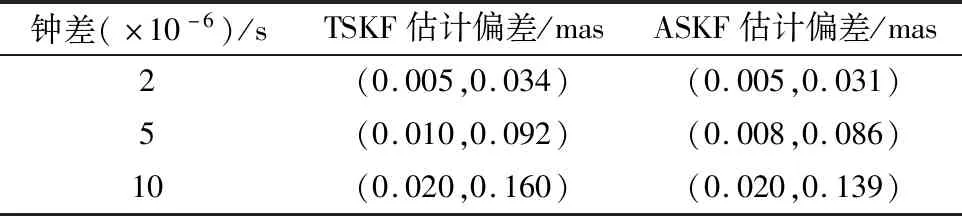
表4 不同钟差条件下两种算法估计偏差Table 4 Estimation bias of two algorithms under different

由上述分析可知,本文提出的TSKF算法估计精度较高,虽略低于ASKF算法估计精度,但处于可控范围内,而TSKF算法计算量显著低于ASKF算法,具有更高的运算效率。

为验证TSKF算法的鲁棒性,分析当仿真用的噪声方差与数据真实方差不一致时的估计结果。仿真时将真实值的观测噪声增大3倍,其他条件不变,即仿真中观测噪声方差R=(0.077 69 km)2,而真实值的观测噪声为0.233 07 km,估计结果如图6所示。

分析图6可知,当仿真用的噪声方差与数据真实方差不一致时,在0～50天赤经估计误差略大于图4估计结果,但估计结果也能在第80天左右收敛到2 mas左右。在0～100天赤纬估计结果偏差大于图4赤纬估计结果,但在第100天后也能收敛到2 mas左右。可见,TSKF算法在仿真用的噪声方差与数据真实方差不一致时,仍能使估计结果收敛到无钟差影响的状态下。

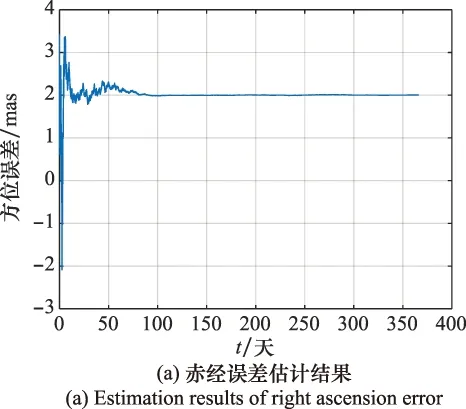
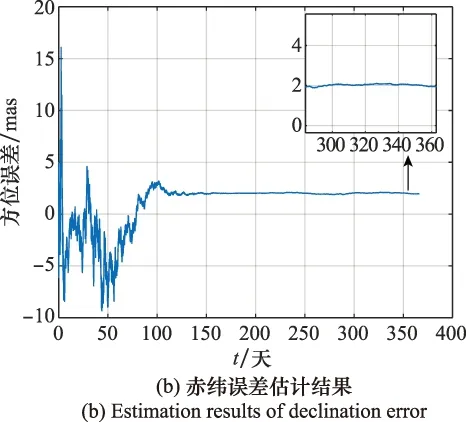
图6 噪声不一致时的估计结果Fig.6 Estimated results with inconsistent noise

由于时钟钟差主要由初始钟差、钟差漂移率和钟差漂移率变化率确定,因此为进一步验证本文算法的鲁棒性,在原钟差模型的基础上添加周期项:

(30)

式中,A0和B0为幅值;Ts为卫星轨道周期。仿真时,钟差真实值采用上述带周期项的模型,幅值A0和B0都取为1×10-6s,其他条件不变,得到估计结果如图7所示。

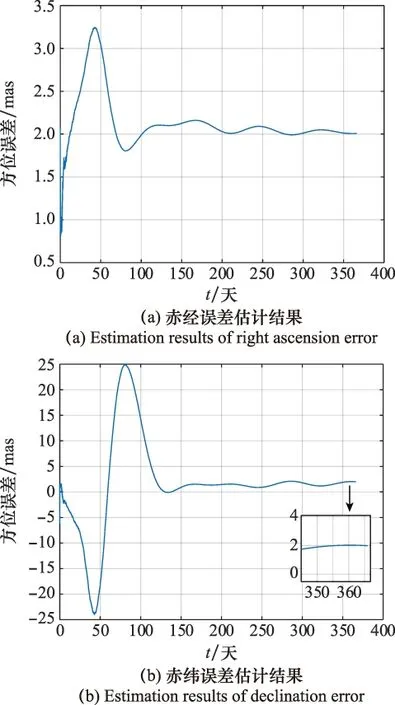
图7 增加周期项的估计结果Fig.7 Estimated results of increasing period item

其他条件不变,选取不同幅值A0和B0的大小进行仿真实验,每次仿真实验进行20次,并选取最后6天的估计结果取平均值,估计结果如表5所示。

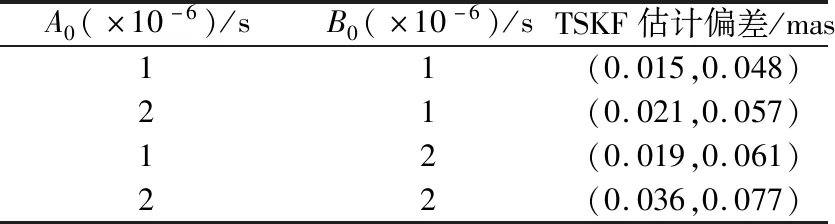
表5 不同幅值条件下的估计偏差Table 5 Estimation bias under different amplitude conditions

分析上述图表可得,当钟差中加入周期变化值而与模型值不一致时,虽然仿真前期偏差较大,但随着时间的推移,估计结果仍能收敛到2 mas左右。虽然与模型一致时会在2 mas附近上下抖动,但这种抖动幅度是微小的,可以通过取平均值的方法来提高精度,也验证了TSKF算法具有较强的鲁棒性。

4 结 论

(1) 利用航天器(信标卫星)进行脉冲星方位误差估计时,航天器的时钟钟差会造成系统偏差,对估计结果产生影响,且这种偏差和影响是不容忽略的。

(2) 考虑钟差修正的TSKF算法能有效隔离时钟钟差对脉冲星方位误差估计的影响,在保证滤波解算稳定性的同时,能使估计精度保持在无钟差影响下的水平。

(3) 与ASKF算法相比,TSKF算法具有相近的估计精度和更高的运算效率,且TSKF算法具有较强的鲁棒性。