基于优化序列提取的相控阵雷达识别方法
刘 傲,周 正,李双明
(海军航空大学,山东 烟台 264001)
0 引 言
相控阵雷达作为一种新体制雷达,具有多种功能并行的特点,使得电子支援措施(electronic support measure,ESM)难以识别出其工作状态及其他信息,给辐射源识别带来很大挑战[1-3]。
国内外学者对雷达辐射源识别做了很多研究。从序列分析的角度,文献[4]提出了一种适用于具有未知规则性的雷达信号序列预测状态表示法;文献[5-7]将相控阵雷达的工作机制与生物体的细胞做类比,依据两者在系统结构及运行机制上的相似性,把生物基因工程序列分析技术运用到相控阵雷达识别中。从脉内特征方面,文献[8]在时频域提取了奇异值作为特征描述,建立了联合协作表示模型,增加了类间区分度;文献[9]根据双谱变换更能突出信号间差别的特性,提出了基于双谱和加速鲁棒的特征进行识别。在构建新识别模型方面,文献[10]引入一个平滑的权值函数来解决数据偏差问题,在此基础上提出了一种基于加权xgboost的识别模型;文献[11]构建了一种包含卷积神经网络(convolutional neural network,CNN)和Elman神经网络的雷达识别方法,使得在低信噪比下仍有较高准确性;文献[12]利用粒子群优化算法和支持向量机建立模型进行识别,提高了识别精度;文献[13]通过深度CNN的方法,取得了更好的泛化能力和特征表示优势。从信号能量角度,文献[14]计算各频率采样值在不同时间采样下的累积量,得到短时傅里叶变换的能量累积量,通过增强型深信度网络对雷达辐射源进行识别和分类;文献[15]根据信号能量在不同分数阶傅里叶变换域角度的变化,将信号分解成多个分量,结合CNN,取得了较好的识别效果。另外,还有通过参数的不确定性,构造区间参数数据库,结合证据理论完成自适应判决识别的方法等[16]。以上文献大多只是对雷达特征、能量或识别方法的研究,很少从工作模式序列的特点上进行分析,或者分析时效率较低。
相控阵雷达工作时,搜索模式的周期特性使得不同时段截获的信号序列呈现一定的相似性。生物序列分析技术中的Needleman-Wunsch[5-7]算法可有效提取出不同样本中的公共序列,很适合提取雷达序列中的相似部分。本文在Needleman-Wunsch算法的基础上,优化了算法的运算流程,提高了识别效率,在不同跟踪情况下,对相控阵雷达识别准确性和效率进行仿真,得到了较好的效果。
1 相控阵雷达工作模型
1.1 相控阵雷达工作模式的生成
相控阵雷达在对某一目标区域执行搜索任务时,馈电系统会将目标区域分为不同的小区域,使用不同的数据率对其搜索[17-18]。通过波位编排对每个目标区域进行波位划分,为避免波束展宽效应,波位编排一般在正弦空间坐标系中进行[19-20]。正弦空间坐标系下交错波束排列方式如图1所示。

图1 正弦空间坐标系下波束排列图Fig.1 Beam arrangement diagram in sinusoidal coordinate system
相控阵雷达对目标区域进行搜索时,搜索任务执行模块会产生搜索序列,雷达执行搜索任务。因为相控阵雷达对目标区域搜索的顺序固定,每次搜索时目标区域ESM截获的序列就会重复一遍[21-23],所以截获的雷达搜索工作模式序列的类型、数目是固定的,并且具有周期性,这也为提取公共序列提供了依据。
当目标出现,有跟踪需求时,跟踪执行模块会产生跟踪序列以执行跟踪任务,且跟踪任务的优先级要高于搜索任务[24-26]。由于目标与雷达的相对距离和位置,目标的速度和方位信息都是随机的,跟踪执行模块会根据实际情况产生相对应的跟踪序列。因此,跟踪序列的种类、数目等都是随机的,并且会随机插入到搜索序列中。通过雷达任务调动模块整合搜索和跟踪序列,这也产生了搜索与跟踪联合的多模式工作任务。相控阵雷达多模式工作示意图如图2所示。
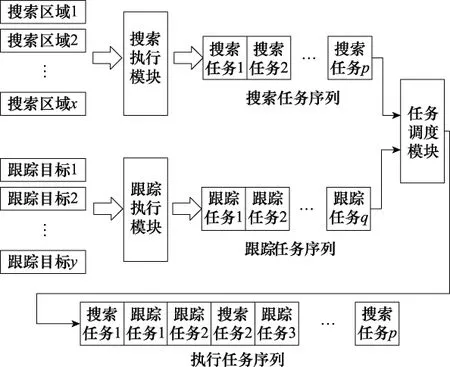
图2 相控阵雷达辐射源多模式工作示意图Fig.2 Schematic diagram of multi-mode working for phased array radar emitter
1.2 建立相控阵雷达工作模式序列模型
对相控阵雷达的不同工作模式序列进行建模,令
TS={TS1,TS2,TS3,…,TSp}
(1)
TG={TG1,TG2,TG3,…,TGq}
(2)
式中,TS为搜索模式序列;TSi为第i种搜索模式;TG为跟踪模式序列;TGj为第j种跟踪模式。
设
T=TS∪TG
(3)
式中,T包含r个元素,且r=p+q。
对搜索、跟踪模式序列及搜索跟踪相结合的多模式序列做如下表述。
令Λ为一个有限集合,其元素为字符符号,Λ*为Λ的Kleene闭包,即Λ*是从Λ中的符号生成的所有可能有限长度的字符串集合。
∀W∈Λ,x,y∈Λ*,引入插入算子IN(·),有如下表示:
IN(x,W)={y|y∈Λ*},y为在x的任意位置嵌入W所得的序列。
两个字符串时,有IN(x,y)={z|z∈Λ*},z为对y中的每个元素W均进行IN(x,W)处理后的序列。则有IN(x,W)⊂Λ*,IN(x,y)⊂Λ*。
s=S1S2…Si…SU
(4)
式中,s为需要提取的搜索模式转换序列。
g=G1G2…Gj…GV
(5)
式中,g为随机序列。跟踪模式时,相控阵雷达跟踪模式序列的选取是未知的,假设各个符号的选取概率都相同,则有
p(Gj=TGi)=1/q,i=1,2,…,q
(6)
式中,p(Gj=TGi)为跟踪模式为TGi的概率。
由搜索和跟踪相结合的多模式序列可表示为
l=l1l2…lk…lK
(7)
根据IN(·)的定义,其中l∈IN(s,g),根据搜索模式的周期性,可得3个不同时间段内的多模式序列l1,l2,l3,这些序列包含3个相似的搜索模式序列s1,s2,s3,则有
(8)
s1∩s2∩s3→s
(9)
式中,符号“∩”表示两序列中的公共序列;“→”表示序列相似。希望在观测序列中提取出相控阵雷达的搜索规律,即在多模式序列l1,l2,l3中提取出公共相似部分s。
2 公共序列提取的匹配方案
对采集的同一部雷达3个不同观测时间段的多模式序列l1,l2,l3进行搜索公共序列提取时,文献[5,7]对采集的序列样本进行时间对准处理,但实际情况下,处理的序列中搜索模式部分不一定为执行搜索序列s的整数倍,很难对准相关序列,而且意义不大,因此本文不对序列进行对准处理。本文提取公共序列时,先将相关序列通过匹配算法算出各序列间的最佳匹配方案,再通过最佳匹配方案找出多模式序列中的公共序列。
不同序列间的最佳匹配方案是指在两两序列的符号间建立一一配对关系,此时允许在序列间插入空白位置,保证相同符号可以对齐,再提取出识别率最高的序列,即为最佳匹配方案。先对利用Needleman-Wunscch算法制定的匹配方案进行介绍。
(1) 拟定评分标准
用评分标准来对不同序列中符号的匹配情况进行奖励和处罚。令
M+=M∪{}
(10)
式中,“”为空白位置。评分矩阵P为l+1阶的Hermite矩阵。
P=(qi j)(l+1)×(l+1)
(11)
式中,qi j表示M+中第i与第j个元素匹配的评分,匹配成功时得分为1,不同或与空位置匹配时得分为-1。若M+中第i与第j个元素分别为A和B,则
q(A,B)=qi j
(12)
序列匹配的评分是指两序列中所有元素匹配评分的总和,要选取的最佳匹配方案是指评分最高的匹配方法,通过引入部分得分矩阵得到。
(2) 构建部分得分矩阵
用部分得分矩阵R来表示序列l1,l2所有匹配方案。R的行和列与l1,l2分别对应。l1,l2的长度分别为n1,n2,假设n1≤n2,则R为
R=(ri j)(n1+1)×(n2+1)
(13)
式中,ri j表示序列l1前i-1个元素组成的分序列和序列l2前j-1个元素组成的分序列最佳匹配的评分。
构建R时,先按照空位评分准则,初始化R的第一行和第一列,再从r22开始计算R中的各个元素ri j,计算式如下:
ri j=max{r(i-1)j+q(L1i,),ri(j-1)+q(L2j,),
r(i-1)(j-1)+q(L1(i-1),L2(j-1))}
(14)
式中,L1i表示l1的第i个元素;L2j表示l2的第j个元素。最终的r(n1+1)(n2+1)即为两序列最佳匹配的评分。再通过追溯得到最佳匹配方案,即两条工作模式序列的公共序列e12。
(3) 提取两序列间的最佳匹配序列
先对部分得分矩阵R进行取值追溯,提取最佳匹配方案。追溯流程为:从r(n1+1)(n2+1)开始,可分别向上、向左和左上移动一格,当追溯到ri j时,在r(i-1)j,ri(j-1),r(i-1)(j-1)中选择满足式(14)的值,继续下一步追溯,直至到r11,最终形成的路径即为最佳匹配方案路径。
追溯完毕后,需在路径中提取最佳匹配序列,方法为:在ri j处,若路径向左移动,则表示在L2j前插入一个空白位置;若向上移动,则表示在L1i前插入一个空白位置;若向左上移动,则表示L1(i-1)和L2(j-1)配对成功。将追溯路径从右下角到左上角依次排列提取出匹配成功的序列,即为两序列间的最佳匹配序列。
上述方法得到的路径可能不止一条,此时所有路径得到的匹配序列均可作为最佳匹配方案,追溯时若有多种情况,人为选定一条即可。
(4) 提取多序列间的最佳匹配序列

(5) 实例分析
设M+={E,F,G,H,},l1=EGHEG,l2=FF·HEGHG。可得评分矩阵P和部分得分矩阵R及追溯路径如图3(a)和图3(b)所示,提取出的最佳匹配序列如图3(c)所示。

图3 最佳匹配图Fig.3 The best matching graph
3 优化公共序列提取方案
3.1 优化算法流程
由图3可知,Needleman-Wunscch算法的计算过程中,得分矩阵追溯路径的两侧存在大量无用数据。计算部分得分矩阵时,这些无用数据会增加运算时间,下面对其进行优化,步骤如图4所示。

图4 优化算法提取最佳匹配序列流程图Fig.4 Flow chart of optimization algorithm for extracting the best matching sequence
3.1.1 寻找匹配元素值
文献[6]中对Needleman-Wunscch算法进行计算时,只模拟了l1和l2中元素个数相同的情况,而实际中这种情况并不常见。文献[5]设定比对序列l1和l2时,各序列元素只有4种,类别较少。本文假定l2中元素个数多于l1,且增加了比对序列元素的种类。计算方式为:将l2作为得分矩阵的行,将l1作为得分矩阵的列,从左上角按斜线开始运算,首先初始化第一行和第一列,算出r22,然后算出r23,r32,再算出r24,r33,r42,直至q(L1(i-1),L2(j-1))=1时,得到第一个两序列匹配的元素,然后进入下一步处理。评分标准的拟定、得分矩阵的构建及得分矩阵元素值ri j的计算方式与第2节相同。设M+={A,B,C,D,E,F,},l1=EFDAF,l2=FECBDABF。可得评分矩阵P和部分得分矩阵R,如图5和图6所示。

图5 评分矩阵PFig.5 Scoring matrix P
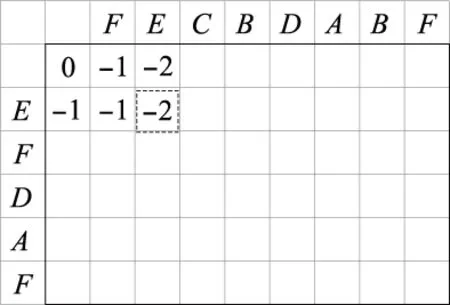
图6 部分得分矩阵RFig.6 Partial scoring matrix R
此时q(L1(2-1),L2(3-1))=1,r23=-2,可知图6虚线框中的元素即为两序列匹配到的第一个公共元素E,再进入下一步运算。
3.1.2 截取序列进行重新对比
总而言之,农村拥有广阔的天地,拥有丰富的教育资源。在农村幼儿园教育教学中,教师应当充分利用大自然中的各种资源,充分利用农村丰富的乡土资源,为幼儿营造一个良好的区域活动开展环境,保证幼儿的个性发展,促进农村幼教事业的不断进步。

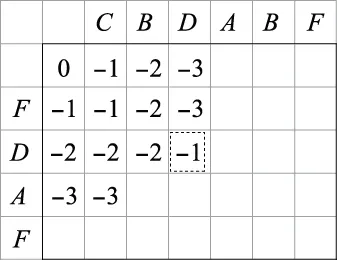
图7 部分得分矩阵R(1)Fig.7 Partial scoring matrix R(1)


图8 部分得分矩阵R(2)Fig.8 Partial scoring matrix R(2)


图9 部分得分矩阵R(3)Fig.9 Partial scoring matrix R(3)
此时q(3)(L1(2-1),L2(3-1))=1,r22=0,可知图9虚线框中的元素即为两序列匹配到的公共元素F,此时两序列已匹配完毕,循环终止。
将以上循环中的各个公共元素,按先后顺序进行提取,可得到比对序列l1和l2的公共序列eend=EDAF。
3.2 算法分析
3.2.1 适用条件
(1) ESM将不同时间段内截获的信息分选后,序列样本均来自于同一部雷达;
(2) 根据第1.1节表述,截获的雷达搜索工作模式序列的类型和数目是固定的,并且具有周期性,这是提取公共序列的基础;
(3) 外界噪声只能影响识别准确率,而不会对计算得分矩阵的元素值、追溯公共元素、截短序列构建新序列等过程的计算时间产生影响。
3.2.2 效率分析

T=T1+T2=(n1-1)(n2-1)t+n1t
(15)
对于优化后的算法,假设所对比的序列中共有k个公共元素,且k>1。公共元素在得分矩阵R中的位置为(pi,qi),其中i=1,2,…,k,根据优化算法的运算规律,从第i个公共元素到第i+1个公共元素的计算过程中,运算时间最多时,即长为(pi+1-pi),宽为(qi+1-qi)的矩阵中所有元素均进行了运算,所需时间为(pi+1-pi)(qi+1-qi)·t。根据之前表述,初始化时间可以忽略不计,可得优化后算法所需时间不超过

(16)
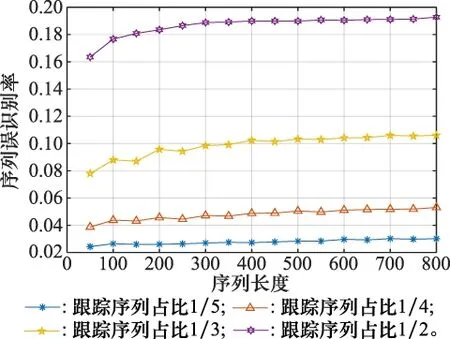
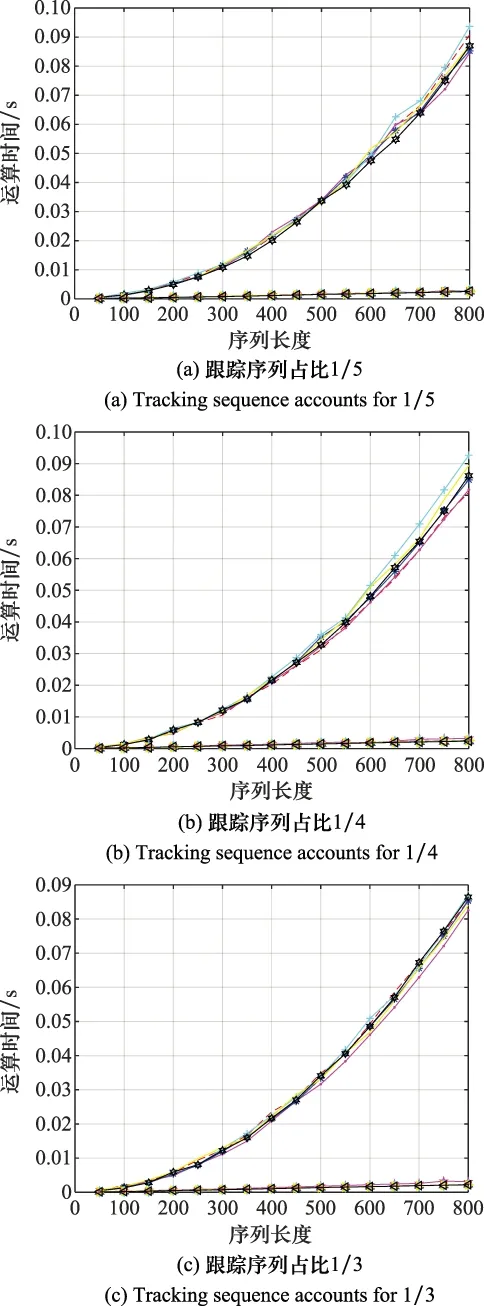
式中,1 (17) 下面通过Matlab对式(17)进行仿真,仿真中引入箱线图。这是通过所得数据中的5个特征值:最小值、第一四分位数Q1、中位数、第三四分位数Q3和最大值来描述数据的图形。第一、第三四分位数间的距离为四分间距IQR,最小值为Q1-1.5×IQR,最大值为Q3+1.5×IQR,Q1为所有数据从小到大排列后第25%的数值,Q3为所有数据从小到大排列后第75%的数值,中位数为数据集的中间值,如图10所示。 图10 箱线图Fig.10 Boxplot diagram 实际情况中,样本序列长度相近,可假设50≤n1<400,50 可在n2分别为200,300,400时,对不同公共元素个数k下的a进行仿真,每种k下进行1 000次蒙特卡罗仿真实验,其中(pi,qi)是在规定范围内任取的随机值。通过箱线图表示的时间比如图11所示。 图11中存在少数异常值,因为实验中的取值是随机的,异常值的存在也属于正常现象。由图11可知,随着序列长度的增加,优化后和优化前的时间比值越来越小,说明随着序列的增加效率越来越高,以序列长度为200,300和400为例,时间比大约为[0.015,0.069],说明本文算法可以有效提高效率。 图11 不同序列长度下优化前后的时间比值Fig.11 Time ratio before and after optimization under different sequence lengths 文献[5]运用Needleman-Wunscch算法时,需要将部分得分矩阵的所有元素值算出,然后进行追溯。本文在计算时,只计算部分得分矩阵对角线周围的元素值,并且通过不断截掉已经匹配完毕的两序列元素,使得运算量大大减少,节约计算资源。整合后的得分矩阵如图12所示。 图12 得分矩阵整合图Fig.12 Scoring matrix integration diagram 图12中虚线框交叠部分,即为两序列的公共元素。由图12可知,整合后的矩阵能更加直接地看出公共元素的匹配情况。 由于相控阵雷达多模式序列是搜索和跟踪模式的联合序列,跟踪模式的插入方式是随机的,所以根据改进算法提取出的公共搜索序列可能与实际搜索序列不同。因此,定义序列识别率Pr和误识别率Pf两个性能衡量指标分别为 (18) (19) 式中,R为算法提取的公共搜索序列中,与实际搜索序列元素顺序和种类完全匹配模式的个数;T为实际搜索序列中模式的个数;N为用本文算法提取的公共搜索序列中模式的个数。识别率Pr表示用本文算法提取出的搜索序列与实际搜索序列的关联程度,误识别率Pf表示将跟踪模式误认为是搜索模式的个数在提取出的公共搜索序列模式总个数中的占比。 为验证该方法的有效性,进行仿真实验。实验1通过对3条相控阵雷达工作模式序列提取公共序列,仿真不同跟踪序列下的序列识别率Pr和误识别率Pf,验证该方法的效果。实验2通过改变跟踪序列模式的种类数,验证该方法对不同跟踪目标下相控阵雷达工作模式的判断效果。实验3通过仿真不同比例的跟踪序列,将改进前后的运行时间进行对比。 实验 1通过仿真序列识别率Pr和误识别率Pf,对本文方法的有效性进行说明。下面对相控阵雷达参数设置做详细阐述。假设搜索模式下8个仰角方向,每个仰角100个波束位置,每个波束位置对应一个搜索序列长度,因此一个搜索周期内任务序列的长度最长为8×100=800,即仿真中的序列长度最长为800。从仰角1到8按顺序搜索,覆盖范围为0°~49°。 搜索和跟踪模式共同工作时,假设搜索帧周期为4.24 s,跟踪的最大目标数设为100个,一个帧周期内最大跟踪序列数为4.24×100=424个,因此仿真中跟踪序列占比只要在424/800内均是合理的。设置每种波形对应一种搜索或跟踪的工作模式,假设已知每种波形对应的工作模式,搜索及跟踪模式下脉压波形对应的工作模式设置如表1所示。 表1 工作模式与波形对应表Table1 Corresponding table of working mode and waveform 设置搜索和跟踪模式序列为 TS={H,I,J,K,L} (20) TG={H,I,J,M,N} (21) 式中,H,I,J,K,L,M,N为工作模式。 跟踪模块产生跟踪序列g1,g2,g3,随机插入搜索序列中,生成相控阵雷达工作模式序列l1,l2,l3。假定3条序列已完成时间对准,序列长度为50~800,跟踪序列占比分别为1/5、1/4、1/3和1/2时,进行公共搜索序列提取的仿真,每种比例的跟踪序列进行1 000次蒙特卡罗仿真实验,得到序列识别率Pr和误识别率Pf,如图13和图14所示。 由图13和图14可知,在增加实验样本时,改进后识别方法的序列识别率保持在91%以上,误识别率保持在20%以下,说明该方法仍能对不同比例下的雷达工作模式序列进行有效公共搜索序列的提取。且当序列长度增加或跟踪序列的占比增大时,序列识别率降低,误识别率提高。这是因为随着序列长度的增加,对每种模式识别的随机性也随之增加,准确率则随之降低。 图13 不同比例跟踪序列下的PrFig.13 Prunder different ratio tracking sequences 图14 不同比例跟踪序列下的PfFig.14 Pfunder different ratio tracking sequences 实验 2本实验比较了不同跟踪模式数q对该方法的影响。在仿真1中,有TS={H,I,J,K,L},TG={H,I,J,M,N},不同字母代表不同的搜索或跟踪模式,即搜索模式数p=5,跟踪模式数q=5。本节实验保持搜索模式数不变,改变跟踪模式数q进行仿真。跟踪目标的不同会导致跟踪模块产生的序列不同,即跟踪模式数q的改变。设置每条序列长度为50~800,搜索模式数p=8,对于q分别为6,8,10,12,14下的不同跟踪序列占比的序列识别率和误识别率进行仿真。每种跟踪模式种类进行1 000次蒙特卡罗仿真实验,得出不同跟踪序列占比下的序列识别率和误识别率如图15所示。 由图15可知,当跟踪序列占比增加时,识别率降低,误识别率升高,占比为1/3时仍能保证95%以上的匹配率和8%以下的误识别率,总体效果较好。且跟踪序列模式数目越多,其识别效果越好,这是因为目标的变化不影响雷达固定搜索序列的排布,随着跟踪模式的种类变多,序列中相近位置相同类型的跟踪模式必然减少,使得相邻跟踪模式区分度更高,因此使得识别效果更好。 图15 不同跟踪序列占比下的识别效果Fig.15 Recognition effect under different proportions of tracking sequence 实验 3文献[5]将生物学上的序列分析技术成功运用到信号序列分析上,较为先进,也达到了识别效果,但计算过程中无用数据较多,增加了运算时间,下面进行该方法与本文改进方法的对比实验。仿真条件同实验2,进行1 000次蒙特卡罗仿真实验,将优化后的运算时间,与文献[5]中算法的运算时间进行对比,得到不同跟踪序列占比下两种方法的时间对比,如图16所示。 由图16可知,不同跟踪序列占比下新方法均比原方法的运算时间少,这是因为原方法的计算过程中无用数据较多,增加了运算时间,新方法只计算了得分矩阵对角线周围的必要数据,剔除了无用数据,计算量大大减少,运算时间随之减少。 图16 不同跟踪序列占比下的运行时间对比Fig.16 Comparison of running time under different tracking sequence proportions 本文主要研究了相控阵雷达工作模式识别问题,通过分析雷达工作模式的序列特点,提出了一种优化的搜索模式公共序列提取方法。实验中增加了样本序列的个数,仿真了跟踪序列不同占比,跟踪序列不同模式数目下该方法对相控阵雷达工作模式的识别准确率,并与改进前的算法进行对比。结果表明,本文方法识别用时少,效果较好,且跟踪序列占比越小,跟踪模式数目越小,识别效果越好,有一定的参考性。 下一步的研究还应考虑应跟踪序列占比增加较多时,如何确保识别率的问题。由于提取公共序列是建立在搜索序列固定且具有周期性的基础上,假设由于环境影响,搜索序列发生变化,如何进行识别也是下一步的研究方向。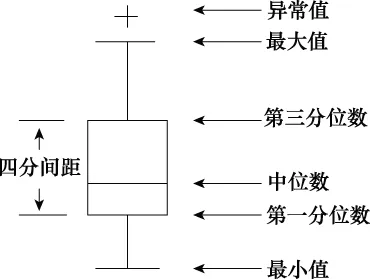

3.3 算法准确性评价准则

4 仿真实验




5 结 论

