基于无人机实时数据多波次任务规划模型分析

胡春宇,刘卫东,于天翔,周立尧,冯 晨

(1.火箭军工程大学基础部,陕西 西安 710025;2.火箭军工程大学研究生院,陕西 西安 710025)

0 引 言

在信息技术特别是大数据飞速发展应用的时代背景下,基于数据的“非接触”信息作战将在未来联合作战中发挥至关重要的作用。未来战争瞬息万变,作战环境越趋复杂、作战威胁越趋严重、作战反应时间越趋快捷,靠单一的导弹部队作战单元难以胜任作战任务需求,就复杂电磁环境来说将面临巨大的生存考验。考虑将无人机与导弹部队作战单元有效融合起来,无人机具有侦察时间长、探测距离远、实时传输快和目标毁伤效果识别好等优势,作战单元提出战场数据需求,无人机集群为导弹部队作战单元实时传输战场数据,两者协同配合,能够使导弹部队在多波次任务规划中产生巨大的作战效能[1]。导弹部队根据无人机提供的战场态势、道路交通情况、隐蔽伪装路段、敌精确打击制导武器等信息数据,迅速判明情况,可以有效确定最优机动路径的选择、火力单元的分配方式、保障单元的编组运用等方案。在明确了火力打击目标命令后,如何利用最短的时间机动至预定阵地,准时完成火力发射任务,基于数据的量化分析和建模评估就变得更加重要[2]。本文将考虑基于无人机提供的数据信息,构建基于路径的多波次任务规划模型。

关于多波次任务规划,国内外进行了相关研究,取得了相应的成果。文献[3]展开了基于遗传算法的任务规划研究。文献[4]研究了具有优先约束的单车任务规划的高效启发式算法。文献[5]提出了基于高斯干扰蚁群算法的无人机任务规划优化。文献[6]研究了基于毕达哥拉斯速度曲线的目标同时攻击的多无人机任务规划。文献[7]研究了基于多自主卫星星座协同下的任务规划任务分配策略。由于各方面因素,国外虽然在任务规划方面研究较多,但对于多波次导弹发射任务规划的研究较少,国内在关于多波次导弹发射研究相对较多。赵国宏[8]、谢苏明[9]等对于导弹部队任务规划认识和建设方面进行了理论研究。文献[10]对于多波次导弹作战构建了马尔可夫链模型并展开了研究分析。文献[11]提出了基于改进单亲算法的多波次导弹发射最优火力分配。文献[12-15]重点从最短机动距离和追点暴漏时间方面研究了多波次导弹发射中的规划问题。

多波次导弹发射任务规划是一个复杂的过程,不是单一的线性作战问题,各波次之间受制约因素也较多。多波次任务规划过程中,第一波次任务结束后需要机动至预定作战阵地实施下一波次的任务规划,下一波次的规划受上一波次的影响。影响任务规划有时间、空间、路径等方面的因素,本文重点以机动路径为出发点,研究基于路径的多波次任务规划。多层规划模型[16-18]对于解决具有递阶关系的优化问题具有独特优势,且在如交通运输[19-21]、工程实践[22-23]和经济领域[24-25]中有着重要的研究作用。针对导弹部队机动问题,借助于多层规划的原理,建立相关的数学模型,不仅使每个路径最优而且整体路径选择最优,并设计相应的算法,最后得出最优路径选择,为任务规划提供科学的理论依据。在进行多波次规划模型求解时,诸多学者提出了形式各异的算法来求解,如蚁群算法[5,15,26]、遗传算法[3,27]、极点搜索法[28]、局部搜素法[29]、禁忌搜索法[30-31]等,这些算法能够解决相应的多层规划问题,但是有各自的使用条件。本文遗传算法和禁忌搜索混合算法,发挥遗传算法能够继承最优个体的优点,又避免了重复个体最优导致无法形成有效的遗传循环。

1 导弹旅作战对无人机实时数据的需求性分析

因导弹武器系统的独特地位和作用,在未来联合作战中主要承担中远程火力打击任务。就导弹旅实施独立作战而言,在向作战区各个阵地机动途中,运用其自主的侦察保障力量,存在以下主要缺陷。

(1) 战场态势不明朗。导弹旅常态化利用夜暗条件机动,在极端恶劣条件下作战,对作战区内可能发生的突发情况掌握不清,地形地貌、交通要塞、敌侦察卫星临空等情况不能及时掌握,影响指挥员的判断和指挥控制,需要实时回传战场态势,才能打破战争迷雾。无人机具有探测距离远、续航能力强的特点,通过精准作战筹划、分组运用,可以实现全程全天的侦察,通过与导弹旅有机融合,形成立体化“全程侦、重点抗、按需援”的作战优势。

(2) 精准保障不到位。打仗某种意义上讲的就是打保障。受导弹分队自身武器装备的力量,能够满足部分地域的信息侦察,但是在复杂战场环境下,作战运用手段和战术运用方式单一化,指挥决策上的主观性与客观上的复杂对抗不相匹配。综合运用无人机的作战力量编组,统一指挥、体系联动、多机协同、适情使用,无人机能够进行对地、对空、对天不同领域的侦察保障,实现以“点”代“面”的保障模式,在博弈对抗中发挥决策优势。

(3) 指挥控制不灵活。导弹旅作战中,指挥通信手段容易受高原高寒、地势崎岖、丛林山地等地形所受阻,仅依托导弹旅自身的地面通信手段难以满足要求。无人机通过搭载微波、超短波、高速、区宽、自组网等通信中继,升空构建覆盖任务地域的通信节点,可以有效解决“动中通”“山地通”“跨区通”等重难点问题,实现语音、图像、数据等信息的按需传输,确保了指挥通信能够精准传送至末端。

2 模型构建

2.1 模型建立

记x为多波次任务规划中的波次数,y为第i波次的路径,R(x,y1,y2,…,ym)为m波次数的总路径距离,ri(x,y1,y2,…,ym)为第i波次的机动距离,G(x,y)为约束函数,gi(x,yi)为第i波次的约束函数,其中i=1,2,…,m。多波次任务规划不仅使得整体路径最优,还要使得每个波次路径最优,一般要求路径选择最短,得到多层规划模型:

(1)

在多波次任务规划中,每一波次均会经过若干个节点,记为Pi,则路径可描述成:

r1P1→r1P2→…→rjPi→…→rmPi

(2)

由此可得第一波次机动路径的距离为

(3)

第j波次的路径为

(4)

式中,r1Pi表示第一波次任务规划中经过i个节点的路径的距离之和;rjPi表示第j波次经过i个节点的路径的距离之和;S1,i(Pi,Pi+1)表示第一次任务规划中第i个节点和第(i+1)个节点之间的路径距离;Sj,i(Pi,Pi+1)表示第j波次中第i个节点和第(i+1)个节点之间的路径距离,由此可得从第一波次到第m波次所有机动路径的总距离之和为

(5)

式(5)也可表示为

(6)

由此构建的多层规划模型为

(7)

2.2 约束分析

在执行多波次任务规划过程中,作战单元接到作战命令后,展开作战准备工作,而后从待机地域向发射阵地机动,实施战斗发射,发射完毕后返回到转载阵地进行导弹转载,依令机动至下一发射阵地进行下一波次任务。从接到命令-转载完毕整个流程记为一个波次,则作战单元机动选择的路径为整个波次中所有路径集合的子集。同一装备在同一路线机动速度一致,不同装备行驶速度有所区别,所有作战区内的定点保障力量和应急防护力量的能力一致,不考虑出现道路车流量过大造成拥堵而导致装备无法机动情况。由于作战区可能发生遭敌精确打击、敌侦察卫星临空、装备发生故障无法行驶、桥梁道路受阻等客观因素,则可能会出现“会车”“超车”等冲突,会影响整个任务的节奏。依托无人机实时监控战场情况和各作战单元机动情况,计算机中存有通过平时作战模拟仿真训练所采集到的各个道路机动所需时间、装备故障维修时间、技术处置时间、敌卫星侦察监视或遭敌袭扰所需的综合防抗处置时间等,所有时间总和即为到达某一节点的机动总时间:

(8)

式中,ta表示该路径机动所占用的必须时间,为一固定值,其余参数如表1所示。

表1 机动影响因子分析表Table 1 Analysis of maneuver influence factors

2.2.1 “会车”冲突

若不同路径的两辆装备到达某一节点的时间一致,如图1所示。某装备X1和X2由不同节点A和B机动至节点D,假设为同种装备,其行驶速度v*相同,但由于受机动因子的影响,导致X1和X2到达D点的时间会出现交叉,造成在节点CD之间D的E点出现“会车”情况。

图1 某机动段“会车”示意图Fig.1 Schematic diagram of "meeting" in a motor section

消除冲突的策略是:按照“先主战后保障”“先紧急后缓和”“谁先到谁先走”的原则,后走的装备如果有备用路段,且备用机动路径所需时间小于等于原机动路径时间与等待时间之和或与二者之和相差不大的情况下,则启用备份路段。假设X1采用备份路径,此时时间分别为

(9)

否则,原地等待,待前车通过后再继续机动,则此时的时间为

(10)

此时“会车”约束可表示为

(11)

2.2.2 “超车”冲突

如果同一路径上机动时,如图2所示。因装备故障原因、技术处置、综合防抗等因素有可能造成后车追上前车,造成“超车”情况。

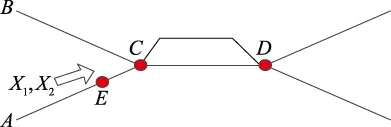
图2 某机动段“超车”示意图Fig.2 Schematic diagram of "overtaking" in a motor section

“超车”条件下的约束可表示为

(12)

消除冲突的策略是:前车主动减速并靠右让行,后车在前车腾出安全距离后实施“超车”,前车待后车通过后再按照原速度机动。

2.2.3 阵地和路径节点约束

考虑到多波次规划中,两个波次不得重复使用同一发射阵地;转载阵地可保证多波次转载任务。在路径选择过程中,相邻的路径节点必须连接,则有如下约束:

(13)

式中,Fj,i(X)表示X型装备第j波次中使用的第i个发射阵地；Zj,i(X) 表示X型装备第j波次中使用的第i个转载阵地；ZT表示转载阵地的总数；Pi,i+1表示相邻的两个节点。

3 基于遗传算法和禁忌搜索算法的混合算法

导弹多波次任务规划问题研究中,最优路径求解的过程为:考虑不同波次之间有递阶关系,第一波次由遗传算法得出,第二波次在上一波次选定路径后,通过无人机反馈的数据信息,采用禁忌搜索,避开第一波次和同一波次中冲突的节点,并完成第二波次的迭代优化,最终确定最优路径。算法流程设计如图3所示。

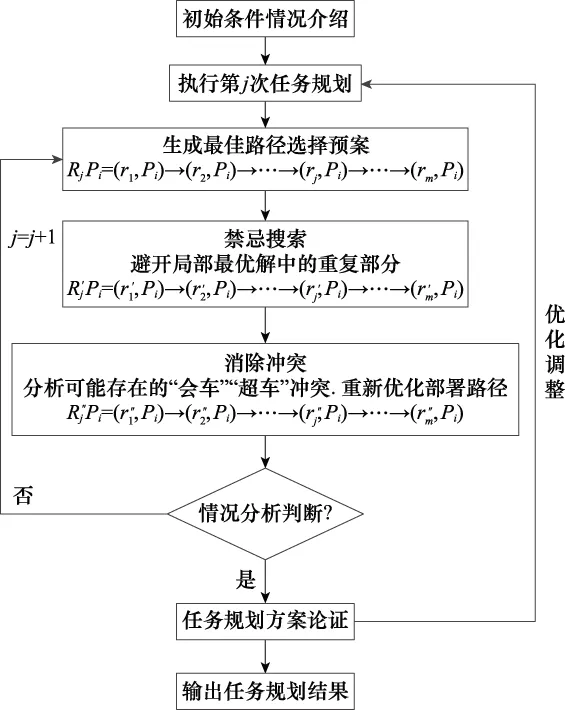
图3 算法流程设计Fig.3 Algorithm flow design

步骤 1根据任务响定中的要求,将数据初始化,将整个任务规划流程划分为“作战准备-作战实施-作战结束与波次转换”3个阶段,并按照一定的规则进行编码,为便于操作计算,采用整数和字母编码方式,编码方案如图4所示,并设置循环次数n。

图4 染色体编码图Fig.4 Chromosome coding diagram

步骤 2对于多波次任务规划中,通过无人机提供的数据信息,计算各个路径节点之间的距离,并用Floyed算法得到初始路径规划方案,生成父代染色体如图5所示,即初始任务规划路径方案。

步骤 3使用旋转赌轮对个体进行选择,将赌轮上的刻度分为与新父代染色体个数相等的份数M,M∈[0,1],每次旋转将得到一个子代染色体,旋转M次,当指针停在哪个区域,则指针所指示的区域中的种群将被选中。

步骤 4采用禁忌搜索方法,排除掉与上一级重复的路径,得出满足适应度的新父代染色体。

步骤 5交叉和变异策略:在任务规划过程中,因路径与路径之间不可避免地会产生交叉点,因此将不同的路径由不同的基因段来表示,从而使得到的子代染色体是可行的,有效避免了无交叉点造成不可行的染色体无法进行循环,增加了复杂度。由于有禁忌搜索和阵地选择约束条件,通过对不同的路径基因段设置变异范围,可得经变异后产生的新染色体与多波次任务规划相适应。

步骤 6重复步骤3～步骤5,直至满足条件。

步骤 7得出最终任务规划方案。

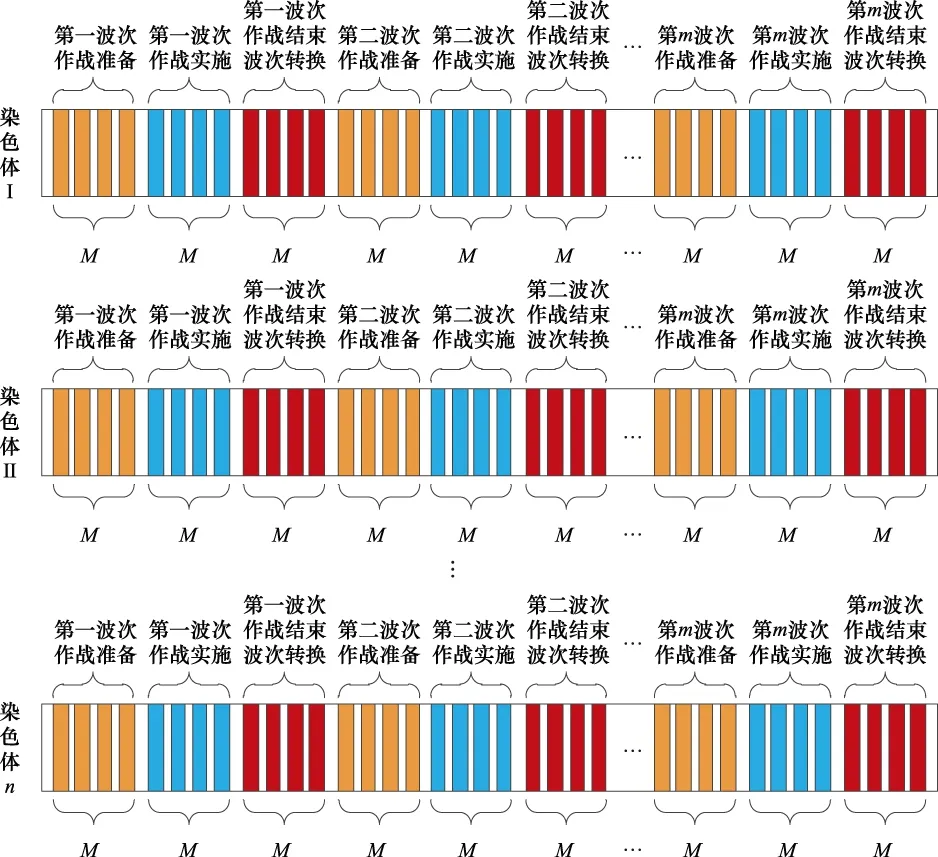
图5 初始父代染色体Fig.5 Initial parent chromosome

4 案例分析

某部执行演训任务,野战化部署于某作战区,区域内设置有待机隐蔽点、转载地域、发射阵地以及路径节点,如图6所示。现有装备X台,进行Y个波次,一个发射阵地只能容纳一个作战单元,一个作战单元可以执行多次任务。

图6 作战阵地节点分布Fig.6 Distribution of battle position nodes

4.1 初始路径选配方案

将作战阵地各个区域按序号编号,作战准备阶段在待机阵地进行准备,作战实施在发射阵地进行,波次转换在转载阵地进行。通过遗传算法求解,得出初始任务规划方案,限于篇幅,只列出部分方案,如表2所示。

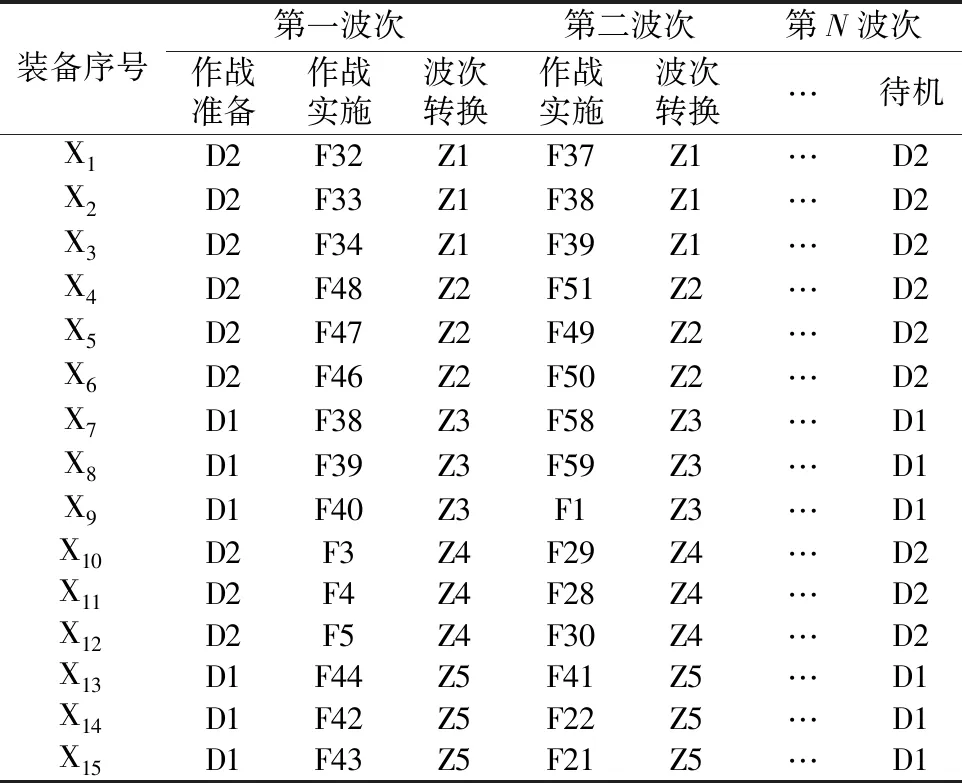
表2 初始规划方案Table 2 Initial planning scheme

4.2 冲突消除及仿真结果分析

根据第2.2.1节和第2.2.2节提到的“会车”和“超车”冲突问题,案例中出现的特殊情况和频率较低,用Matlab进行仿真,得出部分仿真结果图7～图9。

图7 备份路径距离在原路径距离12倍之间仿真结果Fig.7 Simulation results of backup path distance between 12 timesof the original path distance

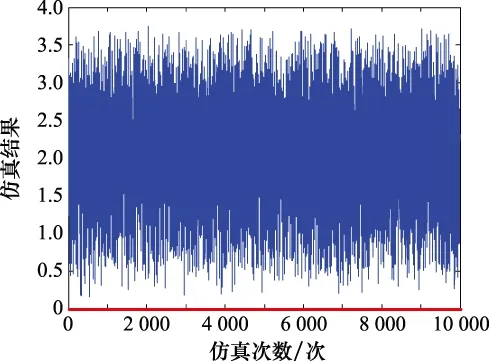
图8 备份路径距离在原路径距离2倍以上的仿真结果Fig.8 Simulation results of backup path distance more than twice of the original path distance

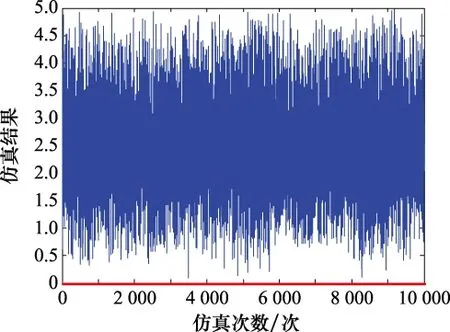
图9 超车冲突示意图Fig.9 Overtaking conflict diagram

通过仿真结果可知,在会车冲突中,当需要绕行选择的路径距离为等待节点所处路径的距离的相近或者2倍以内时,则采用备份路径绕行策略更为合理;若超过2倍,选择在原节点处等待的策略。在超车冲突中,一旦遇到突发情况,将会导致整个过程的时间增加,造成后车超过前车,采用让行通过的策略更加合理。通过消除冲突,使用遗传算法和禁忌搜索混合算法,按照算法设计的流程对路径继续进行调整和部署,得出最终配置方案,限于篇幅,列出部分任务规划路径规划方案如表3所示。

表3 部分任务规划最终路径规划方案Table 3 Final path planning scheme of part of task planning

5 结 论

本文分析了导弹旅任务规划作战对于无人机所能提供的作战数据的需求,提出了导弹旅与无人机协同作战。在此基础上以导弹旅机动路径为例,通过无人机提供的实时信息数据为任务规划服务,并构建了基于无人机实时数据的导弹旅多波次任务规划模型,分析和设计了模型的约束条件,最后利用遗传算法和禁忌搜索混合智能算法进行了求解,得出最佳机动路线。通过仿真案例,模拟了在实际作战中的行车冲突下的应对措施方案,最终得出了整体路径规划方案,验证了模型及算法的可行性。