机载阵列雷达风轮机回波信号建模与分析

何炜琨,刘 昂,王晓亮,张 莹,陈 敏

(中国民航大学天津市智能信号与图像处理重点实验室,天津 300300)

0 引 言

过往研究发现,地基雷达在进行目标监视、气象观测等工作时会受到风力发电场的影响,运作性能受到严重干扰。而对于机载雷达来说,这类影响更为复杂且难以应对[1-3]。为了实现机载雷达风电场杂波抑制和目标检测,研究机载雷达风轮机的电磁散射特性及回波仿真技术尤为重要。

目前,风轮机的电磁散射特性及其回波仿真技术主要是针对地基雷达[4-9],对机载雷达的研究较少。Naqvi[10]利用短时傅里叶变换(short time Fourier transform,STFT)分析了1∶160风轮机计算机辅助设计(computer aided design,CAD)模型散射回波的时频特征,探究雷达处于机载高空平台时,地面反射回波对风轮机散射特性的影响。Bhalla等人[11]利用风轮机CAD模型,发现风电场回波在距离-多普勒谱上会产生伪影,干扰目标信号,影响机载地面运动目标指示(ground moving target indication,GMTI)的性能。另外,Cai等人[12]在研究风电场对多功能机载监视雷达的影响时,认为风轮机叶片材料为理想导体,并利用物理光学(physics optical,PO)方法计算风轮机缩微模型[4,13]的散射回波,但没有给出机载雷达阵列天线风轮机回波信号模型。

上述研究均通过建立风轮机的三维模型,然后再研究其电磁散射特性,但这种方式的风轮机模型制作方法较为困难,不方便修改参数,且操作复杂,计算量大且耗费时间。Mamgain[14]等人对机载监视雷达的风轮机回波进行了仿真,并结合真实数据,通过距离-多普勒谱对所构建的模型进行了验证。但其只给出了单通道的回波模型，没有给出机载阵列雷达各通道风轮机回波,且没有对风轮机回波信号特性进行具体分析,无法全面了解风轮机的回波特征。

目前,阵列天线雷达在机载雷达中的应用越来越广泛,其可以通过空时滤波有效地去除地面杂波,减缓杂波的干扰,在目标监视和气象监测方面发挥着极其重要的作用。基于这种情况,本文将机载阵列天线回波模型与风轮机散射点叠加模型相结合,研究了当雷达处于机载平台时,阵列天线风轮机的回波建模问题,给出任一观测点处机载平台各通道风轮机回波模型,并将实验结果与理论分析结果进行对比,从时频谱、距离-多普勒谱和空时谱多个维度分析了机载阵列雷达风轮机回波的微动特征,验证所建模型的有效性。

1 机载阵列雷达风轮机回波模型

风轮机主要由叶片、桅杆和轮机舱组成。本文结合风轮机散射点叠加理论[15],将风轮机回波等效为一系列薄圆片回波合成[16],构建风轮机叶片的回波模型,并进行特征分析。

图1描述了典型的机载监视雷达场景。其中,以载机所在位置作为原点建立坐标系,飞行方向为Y轴正方向,速度为V，线阵阵元的排列方向为X轴正方向,阵元间隔为d，风轮机相对于雷达的方位角θ为雷达视线(line of sight,LOS)在XOY面内的投影与Y轴的夹角,俯仰角φ为雷达LOS与XOY面的夹角,α和β分别为阵元夹角和速度夹角,波束直接照射风轮机叶片轴心。

图1 风轮机与机载雷达几何关系图Fig.1 Geometric relationship graph between wind turbine and airborne radar

假设雷达所发射的信号为线性调频信号(linear frequency modulation,LFM),令up(t)表示单个LFM的复包络,即

(1)

式中,A为信号幅度;T为脉冲宽度;μ=2πB/T,B为带宽;rect(t/T)为矩形窗函数。

设雷达阵元发射相参脉冲串[17]为

(2)

(3)

式中，Tr为脉冲重复周期;K为脉冲串中的脉冲数。

第n个阵元接收到的单个散射点i的回波信号[17]可表示为

(4)

式中,ar表示散射点回波信号复幅度;τn为第n个阵元接收到的回波信号延时；θi和φi分别为散射点i的方位角和俯仰角;ft(θi,φi)为散射点i由于载机速度所产生的多普勒频率:

(5)

式中，λ为波长。

(6)

则式(4)可进一步写为

(7)

式中，τt=2Ri(t)/c,c为光速，Ri(t)为叶片上任一散射点i到达雷达的距离；li为散射点i到风轮机轴心的距离，由于(li/R)2→0[15],故

(8)

式中，φ(t)为叶片与雷达LOS的夹角;R为风轮机轴心与雷达的距离。因此,由于路径引起的相位差[15]为

(9)

另外,第n个阵元相对于参考阵元的相位差[17]可表示为

(10)

定义该散射点的归一化空间角频率为

(11)

假设雷达发射信号满足窄带条件,则回波信号的复包络在阵元间保持恒定[17],且由式(9)～式(11)可知,式(7)可进一步写为

(12)

(13)

设一个叶片可以分为I个散射点,则整个叶片的回波信号为

exp[j2πft(θi,φi)t+j(n-1)ωs(θi,φi)]·

(14)

设风轮机有G个叶片(一般为3),叶片与雷达LOS相应的夹角为φg(t),于是所有叶片总的回波信号可写为

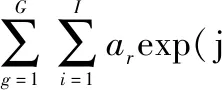
exp[j2πft(θi,φi)t+j(n-1)ωs(θi,φi)]·

(15)

式中,第g个叶片与雷达LOS的夹角余弦值cosφg(t)利用空间两直线夹角公式[15]推导为

cosφg(t)=cosθcosφcosγg(t)+sinφsinγg(t)

(16)

式中，γg(t)为第g个叶片与水平轴Y′负方向的夹角,定义其为叶片夹角。

若j是桅杆上的任一点,其到叶片轴心的距离为mj;桅杆上任意一点j到雷达的距离为Rj[15],则

(17)

雷达第n个阵元接收到的散射点j的回波信号为

(18)

与叶片回波推导过程类似,求出整个桅杆的回波信号并进行下变频,最终得出第n个阵元接收到的桅杆回波信号为

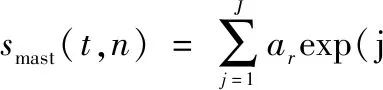
exp[j2πft(θj,φj)t+j(n-1)ωs(θj,φj)]·

(19)

式中,J为桅杆散射点数。因此，第n个阵元接收到的风轮机回波可表示为

sWT(t,n)=sblade(t,n)+smast(t,n)

(20)

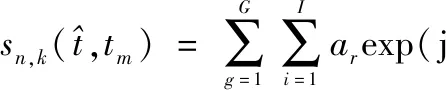
exp[j2πft(θi,φi)tm+j(n-1)ωs(θi,φi)]·

exp[j2πft(θj,φj)tm+j(n-1)ωs(θj,φj)]·

(21)

exp[j(k-1)ωt(θi,φi)+j(n-1)ωs(θi,φi)]+

exp[j(k-1)ωt(θj,φj)+j(n-1)ωs(θj,φj)]

(22)

另外,一般把某一特定距离单元内的风轮机回波对应空时二维数据写入一个N行K列的矩阵:

(23)

式中,N为阵元数；K为脉冲数。通常为方便处理，把单距离单元的接收数据排成一个NK×1的列向量,即x=[x1,1,x2,1,…,xN,1,x1,2,x2,2,…,xN,2,…,x1,K,x2,K,…,xN,K]T。

2 机载阵列雷达风轮机回波信号时频分析

由所建立的机载阵列雷达风轮机回波模型可知,其与地基雷达的风轮机回波模型[15]不同之处在于,由于载机具有速度,在雷达与风轮机径向上的速度分量会产生额外的多普勒频率。同时,由于不同时刻下的载机与风轮机的几何关系不同,导致风轮机与雷达的姿态(如方位角,俯仰角等)发生变化,进而导致风轮机回波信号的微动特征更为复杂。

设载机的飞行高度为3 000 m,选取的风轮机参数参照金风82[20],叶片长度为40.25 m,桅杆高度为70 m,叶片旋转速度设定为15 r/min,风轮机的旋转面假定平行于图1中所建立坐标系的YOZ平面。雷达发射信号为LFM,频率为9.486 GHz,脉冲宽度为20 μs,脉冲带宽为4.687 5 MHz,脉冲重复周期为100 μs,脉冲重复频率(pulse repetition frequency,PRF)为10 kHz[12]。

本文采用STFT对风轮机的回波信号进行时频分析[21],其定义为

(24)

式中,g(t)为窗函数。

假设一个相干处理时间(coherent-processing interval,CPI)内脉冲数为64,载机速度为71 m/s,且在CPI内,雷达与风轮机的相对几何关系不变。

设定风电场中风轮机的方位角θ=0°,轴心坐标为(0,10 000,-2 930)m,雷达位于坐标原点,LOS与风轮机的旋转面平行,风轮机参考叶片夹角为γ=106°,得到风轮机回波信号时频分析结果,如图2所示。

图2 风轮机回波时频分析Fig.2 Time-frequency analysis of wind turbine echo

从图2(a)可以看出,此时风轮机某叶片与雷达LOS垂直且远离雷达,能量分布集中,地基雷达与机载雷达的回波时频谱中出现多普勒闪烁,如图2(b)所示。不同之处在于:一方面,对于机载雷达来说,由于载机本身具有速度,回波信号被调制,风轮机叶片回波产生的多普勒频率在时频谱上平移,同时由于叶片旋转导致其对应的回波在平移的同时产生频谱展宽。另一方面,机载雷达的回波中具有地杂波,同样被载机速度调制,能量在整个时频分析观察时间内集中于载机速度所对应的多普勒频率附近。另外,在0.003 8 s附近,叶片旋转产生的多普勒闪烁与地杂波能量叠加,使得功率归一化后其他位置的归一化功率降低。

经推算可知,载机速度所产生的多普勒频率ft为

(25)

单叶片叶尖回波所产生的最大多普勒频率fWTmax为[15]

(26)

为便于分析不同照射条件下,风轮机叶片的时频谱特性,下面对只有风轮机叶片的回波信号进行时频谱分析。

2.1 叶片夹角对风轮机时频谱的影响

设定风轮机的方位角θ=0°,轴心坐标为(0,10 000,-2 930)m,此时雷达LOS与风轮机的旋转面平行,改变风轮机参考叶片与水平轴的夹角,得到不同叶片夹角的风轮机回波信号分析结果,如图3所示。由图2和图3可以看出,与地基雷达类似的是,在俯仰角和方位角相同的情况下,雷达扫描到风轮机时,由于叶片夹角的不同,导致叶片回波信号的能量分布不同。当风轮机某叶片与雷达LOS垂直时,能量分布集中,时频谱中出现多普勒闪烁。当风轮机3个叶片与雷达LOS均不垂直时,能量分布较为分散。但是由于载机本身具有速度,风轮机回波信号被调制,在时频图上表现为频率搬移,且不同夹角下的搬移程度相同。由于仿真参数中的PRF相对较小,图3时频谱中都有频率折叠的现象。

图3 不同叶片夹角对时频分析的影响Fig.3 Influence of different blade angles on time-frequency analysis

2.2 俯仰角和方位角对风轮机时频谱的影响

在假定风轮机叶片与雷达LOS垂直的情况下,设定风轮机的方位角θ=0°,轴心坐标分别为(0,12 000,-2 930)m和(0,1 000,-2 930)m,得到不同俯仰角的风轮机回波信号分析结果,如图4所示。

由式(5)可知,径向的载机速度分量会根据俯仰角的改变而改变,所产生的多普勒频率也会随之变化。由图4可看出,在方位角θ=0°的情况下,雷达扫描到风轮机时,等效叶片长度不变,垂直叶片转动产生的多普勒闪烁宽度相同,而由于载机运动所引起的频谱平移程度会受到俯仰角的影响:俯仰角越大,平移程度越小;俯仰角越小,平移程度越大。

在假定风轮机叶片与雷达LOS垂直的情况下,设定风轮机相对载机的俯仰角φ=30°,方位角θ分别为37°和53°,轴心坐标分别为(3 000,4 000,-2 930)m和(4 000,3 000,-2 930)m,得到不同方位角的风轮机回波信号分析结果,如图5所示。

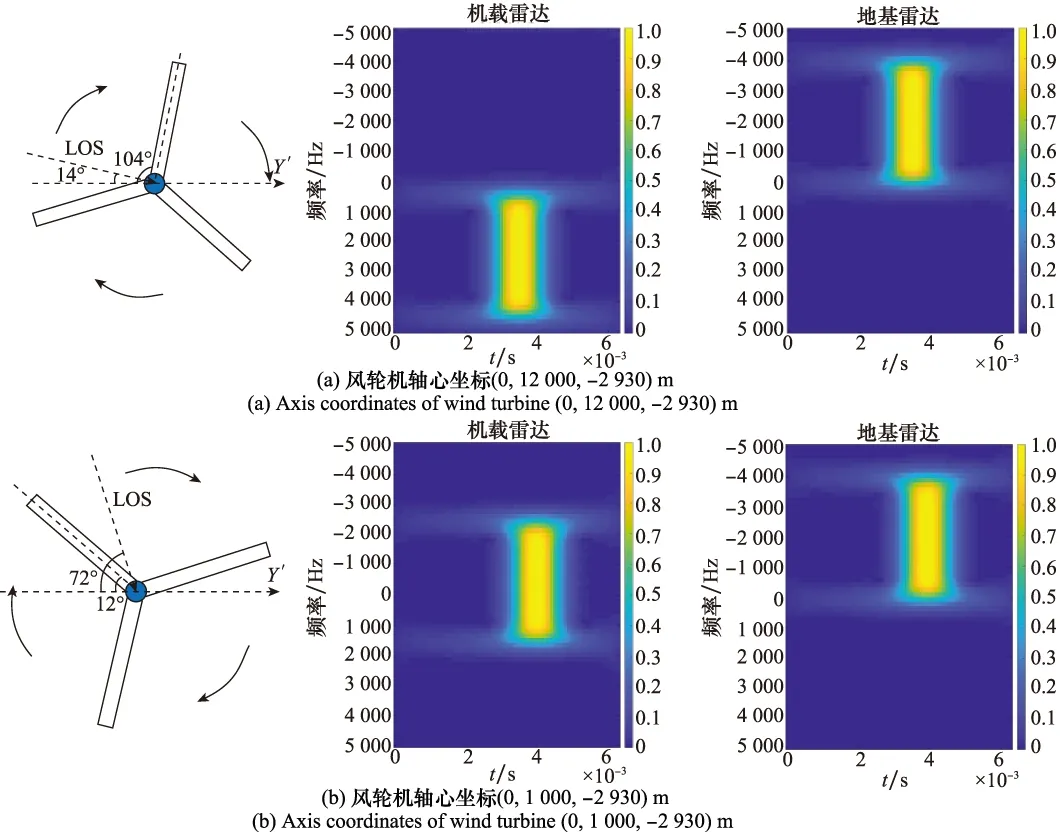
图4 不同俯仰角对时频分析的影响Fig.4 Influence of different pitch angles on time-frequency analysis

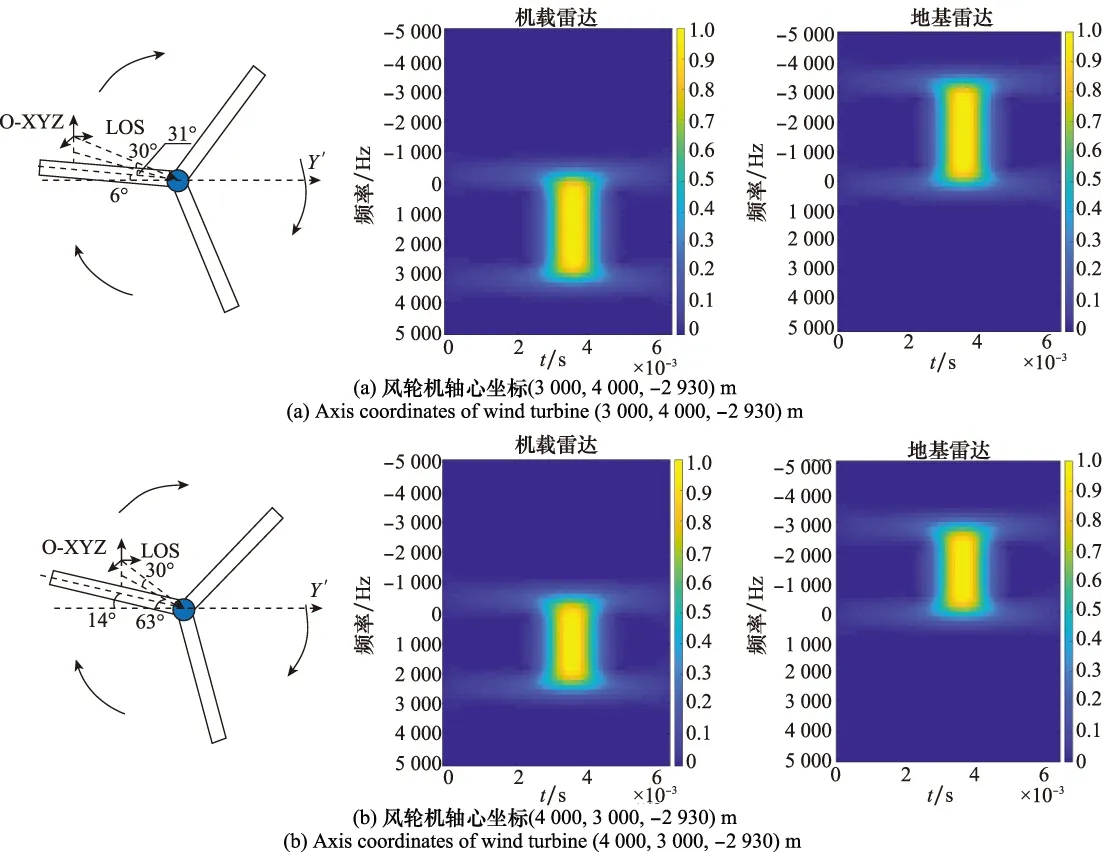
图5 不同方位角对时频分析的影响Fig.5 Influence of different azimuth angles on time-frequency analysis

同理,径向的载机速度分量也会根据方位角的改变而改变,由图5可看出,在俯仰角φ=30°的情况下,不同方位角风轮机所对应的时频谱多普勒闪烁宽度不同,即叶片旋转产生的最大多普勒频率不同,且由于载机运动所引起的频谱平移程度也会受到方位角的影响:方位角越小,闪烁宽度越宽,平移程度越大;方位角越大,闪烁宽度越窄,平移程度越小。

3 机载阵列雷达风轮机回波信号距离-多普勒分析

对轴心坐标为(0,10 000,-2 930) m的风轮机进行距离-多普勒分析如图6所示。经计算得出,风轮机与机载雷达之间的距离为10 420 m,与实验结果相符。从图6中可以看出,当风轮机旋转状态处于图2(a),即叶片夹角γ=106°时,风轮机回波在频域上连续展宽,反射率较强,能量较大。另外,与第1节的时频分析结果相同,由于载机本身的速度,风轮机回波信号被调制,谱图上的展宽在纵轴频域上整体平移。由式(25)和式(26)可以得出,此风轮机回波所对应的ft和fWTmax分别为4 309 Hz和3 998 Hz,与距离-多普勒谱中的表现形式相符。

图6 风轮机回波距离-多普勒分析Fig.6 Range-Doppler analysis of wind turbine echo

同理可以证明,不同叶片夹角、俯仰角和方位角,对机载阵列雷达风轮机回波信号的距离-多普勒特征的影响规律与时频谱的影响规律相同:在载机飞行方向与风轮机旋转面平行的情况下,俯仰角和方位角越大,平移程度越小;俯仰角和方位角越小,平移程度越大。另外,方位角也会影响垂直叶片产生的频谱展宽,方位角越小,展宽越大;方位角越大,展宽越小。

4 机载阵列雷达风轮机回波信号空时谱分析

为了研究机载阵列雷达下风轮机回波的空时域特征,设阵元数为32个,风轮机与雷达的其他参数不变,风轮机的旋转面假定平行于XOY面。

对风轮机进行空时二维谱分析,设定风轮机轴心的位置为(0,10 000,-2 930)m,此时雷达LOS与风轮机的旋转面平行,风轮机参考叶片与水平轴的叶片夹角为106°(见图2(a)),归一化处理结果如图7所示。

图7 回波空时谱(γ=106°)Fig.7 Space-time spectrum of echo (γ=106°)

仿真实验中,风轮机杂波对应的杂噪比为32 dB,地杂波对应的杂噪比为40 dB。由图7可以看出,地杂波在空时谱中表现为椭圆形的分布(天线阵列轴线与载机航向垂直,由空域锥角与多普勒频率之间的关系可知,此时杂波分布为正椭圆),而当风轮机的某一叶片与雷达LOS垂直时,风轮机回波在多普勒域存在明显展宽,总体表现为一条“窄带”。

由风轮机的位置和式(10)可知,其空间角余弦cosα=0,与图7(a)中“窄带”在空域的位置相符。另外由式(25)和式(26)可知,该风轮机回波所对应的ft=4 309 Hz,叶片转动产生的fWTmax=3 998 Hz,且由于此刻垂直叶片远离雷达旋转,所以该情况下的风轮机回波的最小多普勒频率和最大多普勒频率应为fdmin=ft-fWTmax=311 Hz和fdmax=ft=4 309 Hz。根据归一化多普勒频率2fd/PRF可知,风轮机回波所对应的最小归一化多普勒频率和最大归一化多普勒频率应为0.062 2和0.861 8,与空时二维谱中“窄带”在多普勒域的扩展情况相符,理论分析与实验结果一致。

对于机载前向阵来说,地杂波在空时谱上的分布是固定的,但风轮机杂波会在不同的参数下与前向阵的杂波带呈现不同的分布。设定风轮机参考叶片夹角为46°,结果如图8所示。

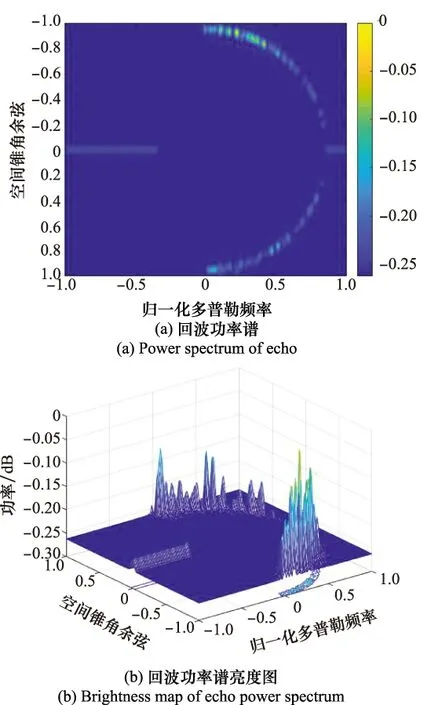
图8 回波空时谱(γ=46°)Fig.8 Space-time spectrum of echo (γ=46°)

由图8可以看出,当叶片夹角为46°时,此刻与雷达LOS垂直的风轮机叶片朝向雷达旋转,产生正向的多普勒频率。风轮机“窄带”由归一化多普勒频率0.861 8处向正向扩展,扩展宽度与叶片夹角为106°时相同。另外,由于PRF的限制,造成多普勒频率折叠。由此可见,对于不同参数下的风轮机叶片,其回波在空时谱中的表现形式不同。

为便于分析不同照射条件下,风轮机叶片的空时谱特性,下面对只有风轮机叶片的回波信号进行空时谱分析。

4.1 叶片夹角对空时二维谱的影响

设定风轮机的方位角θ=0°,轴心坐标为(0,10 000,-2 930)m,此时雷达LOS与风轮机的旋转面平行,改变风轮机参考叶片与水平轴的夹角,与图3一致,得到不同叶片夹角的风轮机回波信号空时谱,如图9所示。

由图9可以看出,随着风轮机叶片夹角的不同,风轮机回波在空时二维谱中所表现的形式也随之不同:当雷达LOS与风轮机某一叶片垂直时(见图7(a)和图9(b)),风轮机回波在多普勒域存在明显展宽,表现为一条“窄带”,且叶片远离雷达和朝向雷达时的“窄带”关于载机速度所对应的归一化多普勒频率点对称;当雷达LOS与风轮机各叶片不垂直时(见图9(a)和图9(c)),由于散射点回波能量相消,在空时二维谱中沿多普勒域能量发散,能量主要集中在叶尖所产生多普勒频率上,同时由于PRF的限制,图9空时谱具有多普勒频率折叠的现象。

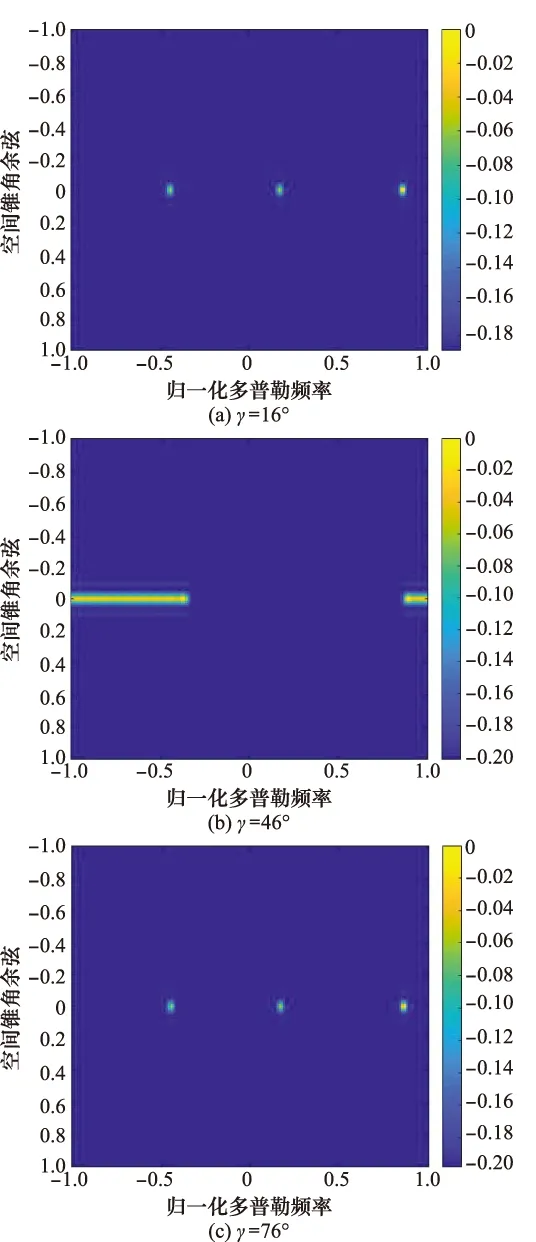
图9 不同叶片夹角对空时二维谱的影响Fig.9 Influence of different blade angles on space-time two-dimensional spectrum

4.2 俯仰角和方位角对空时二维谱的影响

在假定风轮机叶片与雷达LOS垂直的情况下,设定风轮机的方位角θ=0°,轴心坐标分别为(0,12 000,-2 930)m和(0,1 000,-2 930)m,此时雷达LOS与风轮机的旋转面平行,得到不同俯仰角风轮机回波信号的空时谱,如图10所示。

在假定风轮机叶片与雷达LOS垂直的情况下,设定风轮机相对载机的俯仰角φ=30°,方位角分别为37°和53°,轴心坐标分别为(3 000,4 000,-2 930)m和(4 000,3 000,-2 930)m,得到不同方位角风轮机回波信号的空时谱,如图11所示。

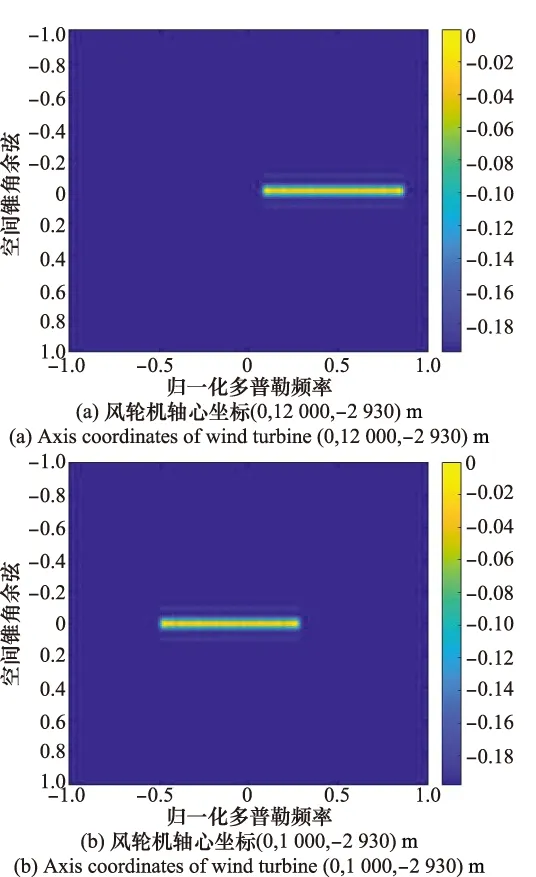
图10 不同俯仰角对空时二维谱的影响Fig.10 Influence of different pitch angles on space-time two-dimensional spectrum

图11 不同方位角对空时二维谱的影响Fig.11 Influence of different azimuth angles on space-time two-dimensional spectrum

由式(10)可知,当方位角θ=0°时,图10(a)和图10(b)中风轮机回波的能量都集中在cosα=0附近,而两者叶片转动产生的最大多普勒频率相同,所对应的“窄带”宽度相同。不同之处在于由于俯仰角不一样,载机速度在风轮机径向方向上的分量不一样,影响“窄带”在多普勒域的位置。当俯仰角φ=30°时,风轮机的空间锥角余弦值随着方位角变化而变化,方位角越大,cosα值越大,如图11所示。另外,由于两位置风轮机的等效叶片长度不同,转动产生的最大多普勒频率不同,所对应的“窄带”宽度有所差异,方位角越大,“窄带”宽度越小。

5 结 论

本文以风轮机为研究对象,建立了对于机载阵列雷达任一观测点处的风轮机回波信号模型,从时频域、距离-多普勒域和空时域对该情况下的风轮机回波信号微动特征进行分析,结果如下。

(1) 风轮机回波信号在机载平台下的表现形式与地基雷达不同,主要区别在于,地基雷达与风轮机的位置都是固定的,风轮机的位置参数不变。而对于机载雷达来说,由于雷达平台的运动,风轮机相对载机的方位角和俯仰角信息会不断改变,其微多普勒特征也会随之变化。

(2) 雷达平台自身的速度会使风轮机的回波信号得到调制,使得风轮机叶片转动产生的多普勒频率在时频谱、距离-多普勒谱和空时谱的多普勒域整体平移,而俯仰角和方位角会影响平移的程度,在0°～90°的范围内,俯仰角和方位角越大,平移程度越小;俯仰角和方位角越小,平移程度越大。

(3) 除平台速度会对回波信号调制,影响其在时频谱中的表现形式外,风轮机相对平台的位置和叶片夹角也会影响风轮机回波信号的时频特征。当平台的运动方向与风轮机的旋转面平行时,风轮机叶片与雷达LOS非垂直情况下的回波信号在时频谱中的能量分布比较分散,而当风轮机叶片夹角改变使得叶片与雷达LOS垂直时,能量分布集中,时频谱中出现多普勒闪烁,方位角会影响闪烁的宽度:方位角越小,闪烁宽度越宽;方位角越大,闪烁宽度越窄。

(4) 当平台的运动方向与风轮机的旋转面平行时,不同叶片夹角的风轮机回波在空时二维谱中的表现形式不同。叶片与雷达LOS垂直时,其频谱特征表现为一条“窄带”;叶片与雷达LOS不垂直时,其频谱能量较为发散,主要由各叶片的叶尖产生。俯仰角固定的情况下,风轮机相对雷达的方位角会影响回波最大多普勒频率及空域角频率,在0°～90°的范围内,方位角越大,空间锥角余弦值越大,最大多普勒频率越小;方位角越小,空间锥角余弦值越小,最大多普勒频率越大。