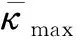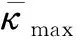软体尺蠖爬行机器人建模与仿真分析

张力文， 徐齐平， 刘锦阳

(上海交通大学 工程力学系， 上海 200240)

不同于具有高刚度和复杂结构的传统刚性机器人，软体机器人具有结构简单、人机交互安全性强、灵活性高、与复杂工作环境兼容性好的优点，是目前机器人行业中最具吸引力的领域之一.软体机器人主要利用形状记忆合金、橡胶材料、硅胶、介电弹性体及芳纶纤维等柔性材料制成[1-5]，能够完成蠕动、游动、越障、跳跃及抓握等复杂的动作[6-10].其驱动方式主要包括流体驱动、形状记忆合金驱动及电活性聚合物驱动等[11-13].

目前，软体机器人的研究还处于起步阶段，研究者们通常从自然界生物的外形结构和运动模式获得灵感，设计适用于特殊环境作业的仿生机器人.Rafsanjani等[5]研制出了一种由硅橡胶管组成的蛇形机器人，当机器人充气膨胀时，附着于机器人表面的可拉伸的塑料薄片会被迫弹出，从而锚定于地面上，整个机器人即可利用这些锚定的塑料片的拉动前进，这种蠕动爬行的运动方式为众多仿蠕虫和仿蛇的软体爬行机器人的运动研究提供了新思路.王江北等[14]设计了一种多气囊软体爬行仿生机器人，通过对其硅胶材料的本构关系的研究，得出了机器人的运动步幅和内部气压的关系，并利用实验验证了该理论关系的可行性，为此类气动驱动的软体爬行机器人爬行步幅的实验研究提供了理论指导.

在所有的仿生软体爬行机器人中，尺蠖形四足软体爬行机器人灵活性好、实用性强，是很多科研人员的重点研究对象.哈佛大学的Shepherd及其团队对该类四足软体爬行机器人进行了实验研究，通过对机器人四肢上简单的阀门系统进行充放气控制，可实现四足之间的协调运动，从而能完成较为复杂的爬行动作[15].随后，他们还利用高弹性硅胶材料制造出了抗干扰性更强的软体机器人，该机器人由电动空气压缩机驱动，可以在严寒、炎热等恶劣条件下长时间自主行进，并能抵抗高强度冲击、碾压等不利因素的干扰[16].虽然Shepherd及其团队对四足软体爬行机器人的结构、材料、运动步态以及适应能力进行了系统的研究，但是未对软体机器人的建模进行深入研究.

气动驱动的软体机器人由多个气腔构成，对其进行力学建模是一个复杂的过程.目前，对气动驱动的软体机器人的建模方法主要包括两种：基于欧拉伯努利理论的曲梁建模方法和非线性有限元建模方法.加州大学伯克利分校的O’Reilly等[17-18]用曲梁建模方法对四足软体爬行机器人运动时和地面的黏附情况进行了建模和理论分析，得出了与地面线接触情况下软体机器人运动的稳定性条件.随后，他们还对于该类机器人和地面的摩擦接触情况进行了分析，提出了一种能够预测其运动方向的基于摩擦定律的弹性杆理论模型[19].文献[20]还基于已经得出的稳定性条件和摩擦模型，将四足软体爬行机器人的力学模型简化为曲梁模型，对该类机器人的运动情况进行了理论上的建模和分析.然后，他们继续通过实验和理论推导，得出了四足软体爬行机器人单个气动致动器的曲率、弯矩以及内部压强之间的关系，实验上验证了理论模型的正确性[21].此外，Majidi等[19]基于欧拉伯努利曲梁模型和库伦摩擦理论建立了机器人运动方向和接触面上摩擦力之间的理论关系.Matia等[22]采用基于欧拉伯努利梁模型估算了驱动的气压和变形之间的函数关系.Suzumori等[7,23]采用非线性有限元方法进行仿真计算，能够得到相对准确的结果，但是计算时间较长，仿真效率较低.

以上学者对尺蠖四足软体爬行机器人的运动提出了较为完善的理论模型，但是他们在研究过程中未考虑软体机器人在不同运动阶段之间的联系，因此也未能反映机器人在整个运动周期内的连续变化情况.

本文针对软体尺蠖爬行机器人建立了滑块-曲梁的简化模型，并对运动控制方程进行离散和无量纲化，利用牛顿迭代法求解准静态条件的边值问题.首先对软体机器人在气压作用下的弯曲变形进行仿真，通过静力学实验验证了理论模型的可行性，在此基础上分析了软体机器人在整个运动周期全过程中的姿态变化、行进运动规律情况.通过对所得结果进行详细的讨论和分析，得到软体尺蠖机器人爬行运动的一般性规律，对于仿生爬行机器人的设计和运动分析具有一定的指导意义和价值.

1 软体尺蠖爬行机器人的简化力学模型

1.1 运动过程的描述

在初始状态下对软体尺蠖机器人充气，可使其获得一定大小的初始曲率，如图1所示.本文利用具有初始曲率的曲梁表示机器人的弯曲构型，从而把整个软体机器人简化为由刚性滑块和曲梁构成的简化模型，称之为软体尺蠖机器人的滑块-曲梁模型[8]，如图2所示.图中曲梁的线密度为ρ，滑块的质量为ms，重力加速度为g，假设水平向右为E1方向，竖直向上为E2方向，建立整体坐标系OE1E2，原点O位于初始条件下滑块与曲梁的连接处，且假设曲梁中线上任意一点沿E1方向和E2方向的坐标分别为x、y.

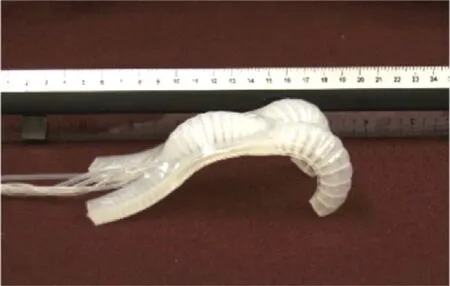
图1 软体尺蠖机器人Fig.1 Soft inchworm-like robot

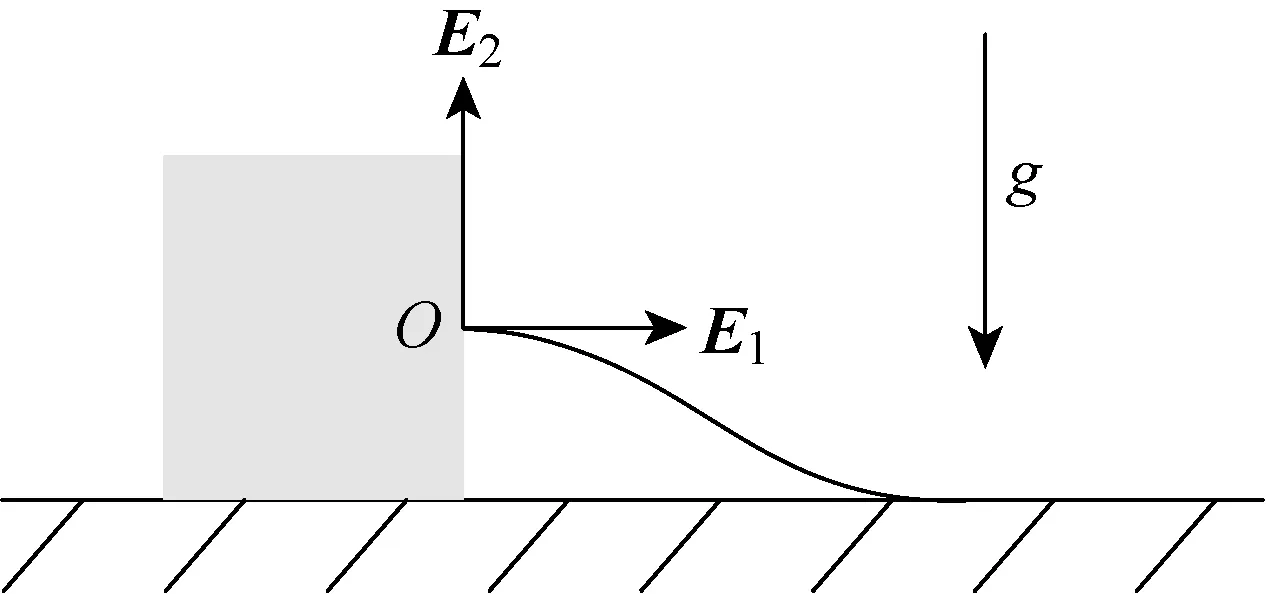
图2 滑块-曲梁模型Fig.2 Slider-curved beam model

图3 切向量r′(s)Fig.3 Tangential vector r′(s)

设曲梁中轴线上某一点距离其最左端处的弧长为s，曲梁总长度为l，该点处曲梁中轴线的切向量为r′(s)，如图3所示.假设曲梁上处于0和s之间的任意一点的弧长为ξ，则切向量相对E1方向的姿态角θ为s的函数，其中，

(1)

设曲梁的初始曲率为κ0.根据 O’Reilly 的研究发现，初始曲率与气腔内的气压成正比[21]，因此可通过控制κ0的变化对软体机器人的运动进行控制.本文采用的κ0具有如下形式：

(2)

由于未知量的个数以及边界条件的不同，将软体尺蠖机器人在整个运动周期的运动状况划分为3个不同的阶段，如图4所示，图中Δ为位移大小.

根据软体机器人的实际运动状况，其在一个周期内的3个不同阶段的大致特征为：

(1) 阶段C：机器人部分黏附于地面，随着滑块曲梁的初始曲率幅值从0逐渐开始增大，滑块逐渐向右滑移，曲梁和地面的黏附部分长度也逐渐减少，即曲梁与地面逐渐剥离直到完全脱离，从而过渡到阶段A.

(2) 阶段A：机器人右端和地面点接触，且该接触点和滑块都黏滞不动，随着曲梁的初始曲率幅值减小，曲梁右端点处所需的摩擦力逐渐增大，该点逐渐产生向右滑移的趋势.当曲梁的初始曲率幅值减小到一定值时，曲梁右端点开始滑移，从而过渡到阶段B.

(3) 阶段B：机器人右端仍然和地面点接触，滑块仍然处于黏滞状态，但是曲梁的右端点会向右滑移，随着曲梁的初始曲率幅值减小，该点逐渐向右移动直到初始曲率幅值减小到0，此时曲梁右端会开始贴附于地面，回到阶段C.

可见，软体尺蠖机器人完全可以通过上述3个不同阶段之间的过渡和转换，完成整个周期的运动，并向前滑移一段位移，实现连续向前爬行运动的目的.

1.2 应变能和重力势能

不考虑曲梁模型的轴向变形，假设曲梁上任意一点的轴向应变为ε，轴向应力为σ，设曲梁截面弯矩为M，相应的抗弯刚度为EI(E为弹性模量，I为截面惯性矩).根据O’Reilly由实验得出的结论，曲梁截面弯矩M和曲率的改变量存在线性关系[21]，此处可表示为M=EI(θ′-κ0).假设曲梁截面上任意一点相对中轴线上投影点的位置矢量在中轴线法向上的坐标分量为yu，以曲梁的体积V、截面积A以及弧长l′为积分自变量，由线弹性理论可以得到应变能为

(3)

当曲梁右端和地面点接触时，若以曲梁左端点所在水平线为重力势能的零点位置，在距离曲梁左端点长度为s处的竖直高度为Y(s)，重力加速度的大小为g，则整个曲梁的重力势能WG为

(4)

当曲梁和地面线接触时，设γ为曲梁未黏附段的长度，h为惯性基原点相对于地面的高度，则曲梁上未黏附段的重力势能WG1和黏附段的重力势能WG2可分别表示为

(5)

1.3 外力势能

当曲梁右端和地面点接触时，设接触点处支持力的大小为N1，摩擦力的大小为Ff1，并以沿着曲梁在左端点处为势能零点，设FL=[Ff1N1]T，r(l)=[x(l)y(l)]T，此时由曲梁右端力产生的外力势能为

(6)

WF1=-n(γ)·r(γ).

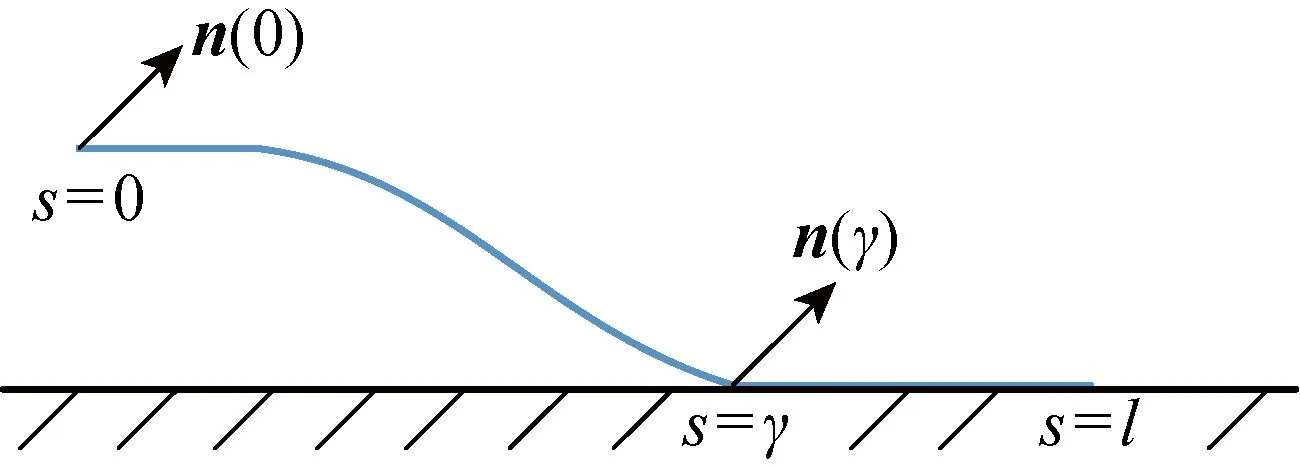
图5 曲梁和地面线接触时受外载荷的情况Fig.5 External force on curved beam when in line contact with the ground

1.4 控制方程的建立

当曲梁和地面点接触时，结合曲梁的应变能、重力势能以及外力势能，可得到点接触阶段中曲梁的总势能V1为

FL·r(l)=

(7)

当曲梁和地面线接触时，曲梁的未黏附段的势能V2为

(8)

(9)

得到该情况下的控制方程的具体形式：

(Ff1sinθ-N1cosθ)=0,s∈[0,l]

(10)

(n1(γ)sinθ-n2(γ)cosθ)=0,s∈[0,γ]

(11)

1.5 边界条件的建立

对于阶段A，曲梁和地面点接触，由于曲梁左端和刚性滑块固接，即θ(0)=0.由于曲梁右端为自由端，并且曲梁右端截面处也无外力矩，则此处的弯矩应该为0，可知M(l)=EI(θ′(l)-κ0(l))=0，即θ′(l)=κ0(l).

曲梁的左端点与滑块固连，以该点为势能零点，该点相对地面的高度为-h，且h>0，从而得到系统在竖直方向的几何边界条件：

在曲梁右端点黏滞的阶段A中，假设了曲梁右端点相对于滑块黏滞，可设两者间距离的大小始终保持为d，则有水平方向的几何边界条件：

综上，可联立曲梁右端和地面点接触时的控制方程以及边界条件，阶段A用于求解的满足给定边界条件的常微分方程组为

(12)

对于阶段B，曲梁右端点滑移.设机器人与地面接触点的静摩擦因数和动摩擦因数分别为μs和μk，则可设曲梁右端处的水平速度为ν(l)>0，阶段B在水平方向的边界条件可写为

此外，在准静态条件下，设滑块和曲梁的相互作用力沿E1和E2方向分量为n1和n2，对阶段B中整个滑块-曲梁系统进行静平衡分析，如图6所示，可以得到相应的静力平衡方程N2=msg+ρgl-N1,Ff1=Ff2.阶段B用于求解的满足给定边界条件的常微分方程组为：

(13)

如果|Ff2|>μsN2，曲梁左端点也发生滑移，Ff2=-μkN2.

图6 阶段B中滑块-曲梁系统的静平衡分析Fig.6 Static equilibrium analysis of slider-curved beam system in phase B

对于阶段C，在曲梁和地面线接触的情况下，由于其在s=γ处的未黏附段右端点即为曲梁和地面接触的起始点，则θ(γ)=0.此外，设滑块和曲梁的相互作用力沿E1和E2方向分量为n1(0)和n2(0)，根据静平衡条件先对滑块进行力平衡分析，如图7所示，得到如下关系式：

(14)

再对曲梁上未黏附段进行力平衡分析，如图7所示：

(15)

图7 阶段C中滑块-曲梁系统的静平衡分析Fig.7 Static equilibrium analysis of slider-curved beam system in phase C

由于滑块在阶段C情况下滑动，设滑块处的水平速度为νh，动摩擦因数为μk，结合静平衡方程得出的表达式，从而得到水平方向的边界条件：

n1(γ)=μkN2sign(νh)=

μk(msg-n2(0))sign(νh)=

μk(msg+ρgγ-n2(γ))sign(νh)

(16)

式中：sign(νh)为符号函数，当νh≥0，sign(νh)=1；当νh=0，sign(νh)=0；当νh<0，sign(νh)=1.

当曲梁和地面线接触时，还需要考虑由黏附作用产生的黏附势能.设曲梁黏附段上单位长度的黏附势能为-ω，曲梁未黏附段的黏附边界条件为[17]

(17)

结合阶段C的曲梁未黏附段的边界条件和控制方程，则得到如下满足给定边界条件的常微分方程组：

(18)

2 软体尺蠖爬行机器人控制方程的仿真分析

2.1 方程组的离散化和无量纲化

在曲梁和地面点接触时，将连续的曲梁划分为n段微段，如图8所示，设其中每一微段的长度为ds，则nds=l.设第i段微段的左端点转角为θi，则si=s(θi)=(i-1)ds.

图8 曲梁和地面点接触时曲梁的离散构型Fig.8 Discrete configuration of curved beam when in point contact with the ground

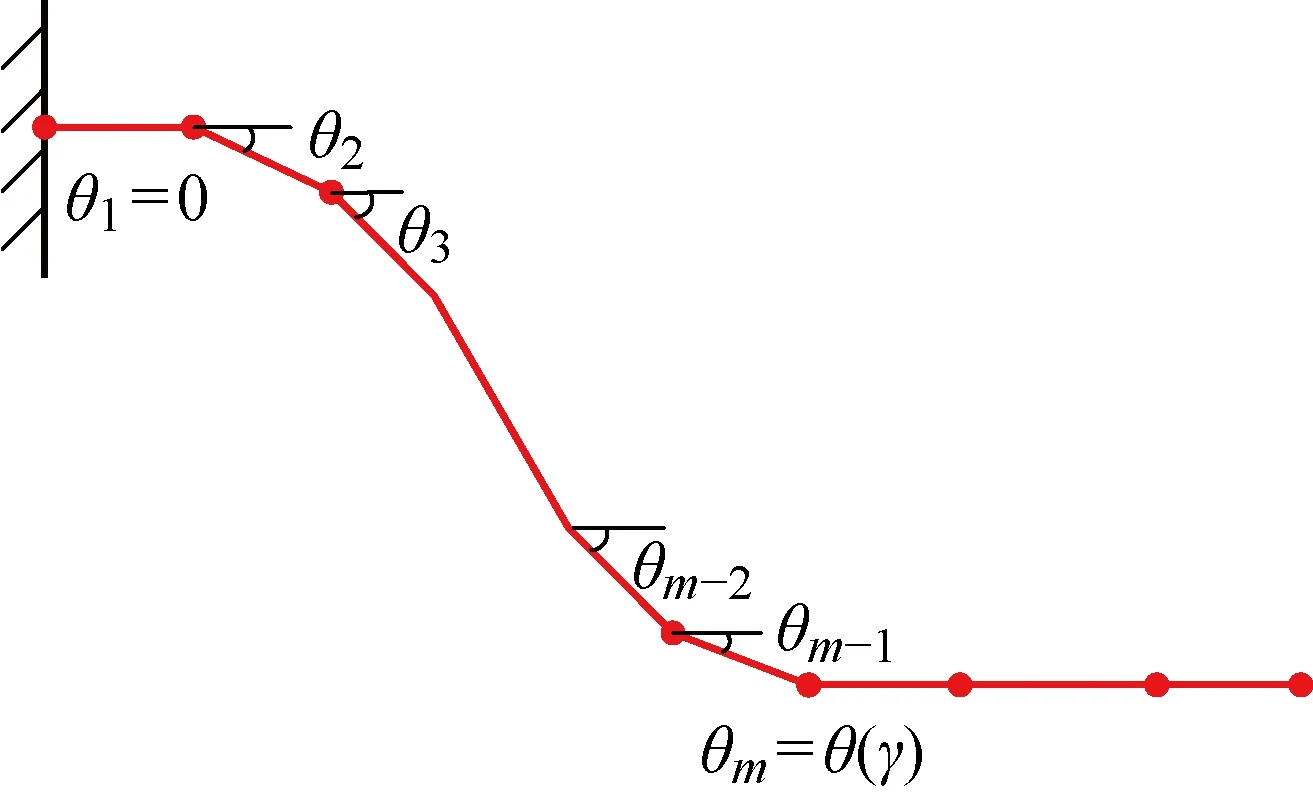
图9 曲梁和地面线接触时曲梁的离散构型Fig.9 Discrete configuration of curved beam when in line contact with the ground

假设曲梁右端末尾还存在第n+1段微段，该段长度仍为ds，且不纳入曲梁的总长之中.则此时方程组的未知量共为n+3个，分别为θ1,θ2,…,θn,θn+1,N1,Ff1.

在曲梁和地面线接触时，由于曲梁黏附段的构型已知，通过离散分析曲梁的未黏附段，完成在微段数目不变，微段长度改变的条件下曲梁构型的求解.将连续的曲梁未黏附段划分为m段微段，每一微段的长度为ds，使得mds=γ，并且其他假设和点接触阶段相同.此时方程组的未知量个数共为m+4个，分别为θ1,θ2, …,θm,θm+1,n2(γ),n1(γ),γ.

本文中对所有的物理量都采取了无量纲化的处理，并将无量纲化的物理量做了新的符号规定，如表1所示.表中L′、F和T分别表示长度、力和时间的量纲.

从而可以写出阶段A最终的离散化、无量纲化的非线性代数方程组：

fn+2=θ1=0

同理，要写出阶段B的离散化、无量纲化的非线性代数方程组，只需采用如下fn+1替换上式中的水平方向边界条件，即fn+1=Ff1+μkN1=0.

还可以写出阶段C最终的离散化、无量纲化的非线性代数方程组：

表1 各物理量的无量纲化Tab.1 Dimensionalization of physical quantities

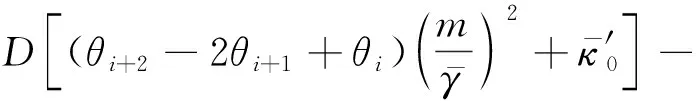
fm+1=θ1=0，fm+2=θm+1=0

2.2 方程组的求解方法

此处将对牛顿迭代法的求解思路以曲梁和地面点接触的情况为例进行说明，而曲梁和地面线接触情况的求解过程与其一致.设方程组在第k次迭代时为列向量F(k)，此时由上一次迭代求得的未知量列向量为X(k)，求导结果构成维数为n+3的方阵即雅可比矩阵F′(k)，并设未知量迭代矩阵为H(k)：

H(k)=-F′(k)-1F(k)
X(k+1)=X(k)+H(k)

2.3 充气变形的静力学实验

为了验证p和κ0之间正比关系的有效性，本文进行了四气腔软体机器人充气变形的静力学实验.将机器人的一端固定，研究其受不同气压载荷作用下的变形状态，如图10所示.

图10 受不同气压载荷作用的软体制动器的变形状态Fig.10 Deformed states of soft actuator subject to different air pressure loads

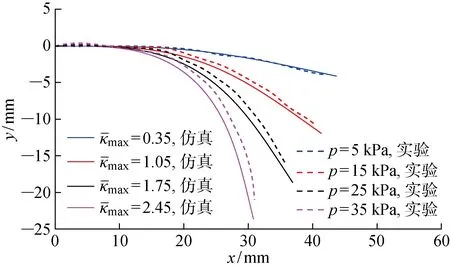
图11 实验和仿真得到的软体制动器变形状态的对比Fig.11 Comparisons of deformation state of soft actuator obtained by experiment and simulation

2.4 机器人运动姿态的准静态实验

为了验证所建立的方程组求解结果的准确性，本文还通过准静态实验研究了长度为44 mm的单臂软体机器人在爬行过程中某一个时刻的运动姿态，如图12所示.单臂软体机器人的特点是左端无姿态约束，滑块的等效质量为0.

图12 实验过程中的软体机器人Fig.12 Soft robot in experiment

在实验过程中，随着充放气不断交替变化，软体爬行机器人逐渐向前运动，在不同的时刻产生了相应的变形形状曲线，其中在时间t=2 s处软体机器人的形状如图13所示.

图13 t=2 s时软体机器人形状的实验和仿真结果Fig.13 Experimental and simulation results of soft robot shape at t=2 s

2.5 点接触阶段的计算结果分析

图14 阶段A在上的构型图Fig.14 Configuration diagram in phase A at

图15 阶段A中曲梁右端外力和的关系曲线Fig.15 External force of right end of curved beam versus in phase A

图16 阶段B在上的构型图Fig.16 Configuration diagram in phase B at

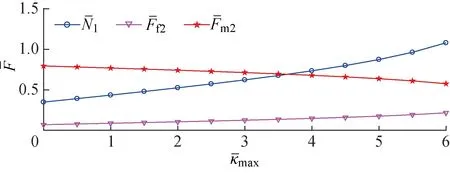
图17 阶段B中滑块-曲梁系统外力绝对值和的关系曲线Fig.17 External force of slider-curved beam system versus in phase B

图18 阶段B中和的关系曲线 versus in phase B

2.6 线接触阶段的计算结果分析

图19 阶段C在上的构型图Fig.19 Configuration diagram in phase C at

图20 滑块的位移和的关系曲线Fig.20 Slider displacement versus in phase C

图21 阶段C中滑块处外力绝对值和的关系曲线Fig.21 External force at the slider versus in phase C

2.7 软体尺蠖机器人的运动周期分析

图22 曲梁在整个运动周期内的构型变化Fig.22 Configuration changes of curved beams during the entire motion cycle

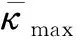
此外，若以阶段C为起始阶段，则也可以获得初始时曲梁左右两端点相对的水平位置距离.根据阶段C的计算结果，曲梁的右端点在初始时的水平投影长度为 0.980 3l.而由阶段B的计算结果，曲梁的水平投影长度在整个运动周期结束时为 0.990 5l，从而得知曲梁左右端点的水平距离在运动周期前后近似相等，意味着整个软体机器人在完成了1个周期的运动后能大致回到运动前的构型和状态，使得每个周期的运动过程近似一致，从而保证了本文的所有计算结果和分析结论对机器人在任意周期运动内的通用性、一致性.

3 结语

针对现有软体爬行机器人的模型在模拟整体运动时的不连贯性、计算效率较低以及在整个周期内未能反映连续运动变化的情况，本文对软体尺蠖爬行机器人建立了滑块-曲梁的简化力学模型，推导了用于数值求解的无量纲离散化的非线性代数方程组，对该机器人的整体运动状况进行了准静态建模和仿真分析.