基于Gaussian混合的距离度量学习数据划分方法

郑德重， 杨媛媛， 谢 哲, 倪扬帆, 李文涛

(1. 中国科学院上海技术物理研究所 医学影像信息学实验室， 上海 200080；2. 中国科学院大学， 北京 100049； 3. 复旦大学附属肿瘤医院， 上海 200032)

近年来，深度学习技术在许多领域取得了巨大的成功，从计算机视觉、网络搜索、社交内容的协同过滤、电子商务的推荐系统，到消费产品中的图像识别、人脸识别等方面的应用都获得了显著提高.深度学习是一种多层次结构化的计算模型，可以从数据中学习多种不同层次的抽象表达[1].仅从数据中学习就可以获得数据不同抽象层次的特征表示，而不需要依赖于特定领域知识进行手工设计是深度学习技术进步的核心[2-3].在训练深度学习模型时，数据常常被划分成多块用于交叉验证，在模型开发中此过程是十分常见又重要的一个环节，因为交叉验证通常可以保证其良好的泛化性能.但对中等规模的数据而言，在进行交叉验证时，划分出来用于测试和验证的子集质量会在一定程度上对神经网络的训练产生一定影响，不良地数据划分会导致所获得的模型不准确，并有可能在交叉验证过程中产生较大的偏差[4-5].小样本数据更是如此，这种规模的数据较难满足统计意义上的普适性和一般随机性.例如，随着人为数据采集的方式和习惯的变化，采集来的数据可能包含着随时间变化的趋势和倾向性特点.因此在使用有限数据时，数据的统计规律是可变的.当数据规模不是足够大时，简单地以随机方式对数据进行划分是不可取的.另一方面，在收集数据的过程中，数据很少是没有噪声的，并且采集来可用的有效数据可能仅仅只占其中一小部分，并不能包含模型构建所需要的全部信息[4].尽管可以通过增加样本量来适当缓解这些问题，但是在一些特定条件下产生的稀有样本并不是那么容易获得的.因此在数据有限的情况下，简单地随机划分数据容易导致测试数据域和训练数据域的漂移，训练所得到的模型是不稳定的.

依据统计学的知识和经验容易知道，准确了解数据和目标的分布特点将有助于理解数据的内在本质，从而合理地划分训练数据和验证数据.由于深度学习技术具有强大的特征提取能力，可以提取与分类目标相关的多种层次的特征.在此基础上，分析样本在特征空间的分布特点有助于更好地理解数据本身，从而合理地划分数据.本文提出一种基于Gaussian混合模型的距离度量学习模型(DML-GMM)划分数据.该方法不依赖于任何特定的特征提取器，在特征提取方面，可以使用任何主流特征提取模型，如ResNet、DenseNet和SENet等模型，在性能方面强于简单随机采样、自组织映射等其他方法.

综上所述，本文做出了如下贡献:

(1) 提出一种新的数据划分方法，与其他数据划分方法相比，使用完全相同的模型结构进行训练能得到更高的准确率、更低的偏差与方差.

(2) 提供一种度量样本相似性方法.通过此方法，可以在分类任务中更准确地了解所采集样本的显著程度和样本分布特点.

(3) 所提出的度量方法还提供了一种在分类任务中获取小概率稀有样本的途径.

1 相关工作

合理的数据划分问题可以视为统计采样问题，因此，可以使用各种经典的统计采样技术来划分数据.在以往的研究中，采用的数据划分方法大致分为以下几种：简单随机采样、系统采样、DUPLEX采样和分层采样.

1.1 简单随机采样(SRS)

简单随机采样是最常使用的方法，其具有高效且易于实现的特点.该方法随机选择分布均匀的样本，每个样本具有同等的选中概率.这种方法的优点是所获得的模型具有低偏差[4].但是，对于更复杂(非均匀分布)的数据集，若划分出来的子数据集不能完全覆盖数据分布的特点会导致模型具有较大的方差[4, 6].

1.2 试错(Trial and error)法

试错法试图通过重复多次随机采样然后取平均来克服SRS中高方差的不足之处[7].简单的试错法表明，在有相同代表性的数据集上，其偏差具有相似的统计特性.为了最小化这种统计差异，使用较为复杂的策略，例如循环优化搜索以寻找潜在的可能拆分组合.使用各种统计学标准，例如均值、方差和Kolmogorov-Smirnov统计.这些方法的主要缺点是计算量大且理论基础模糊，无疑在这种情况下所获得的神经网络性能并不稳定.

1.3 系统采样方法

系统采样是为含有自然序的数据集进行采样的一种确定性方法.一种方法是沿着输出变量的维度对样本数据进行排序，以获取能够代表输出变量分布的样本[8].此方法易于实现，因为其假定可以将输出变量映射到唯一的输入状态.但是，当有多个输入状态产生相同的输出时，此假设可能不适用，并且这种做法不能保证采集得到的样本能够完全代表所有可能的输入和输出组合，因为只有输出变量被考虑到了其中.同时对于大多数类型的数据集(例如多媒体数据、基因序列等)而言，很难找到一种合适的排序.对于无序数据，系统采样的结果与SRS存在相同的问题.系统采样的另一个缺点是对数据集的周期性较为敏感.

1.4 DUPLEX采样

DUPLEX采样方法是由Snee[9]提出的基于欧几里德距离的数据划分方法.应用该方法时，将在欧几里德距离上最远的两个点分配给第1个数据集，再将列表中剩余的样本之间相距最远的下一对点分配到第2个数据集中；重复此过程，直至所有数据分配至要划分的两个数据集中.May等[4]对原始DUPLEX算法进行了修改，将数据划分为3个数据集，分别为由人工神经网络模型开发生成训练、验证和测试数据三部分.

1.5 分层采样

分层采样的基本思想是探索数据集的内部结构和分布，并使用其来划分相对统一的样本组(层、簇).该方法可以确保训练子集完全覆盖输入空间的所有区域.另一方面，对于分布均匀的数据集，可以将分层采样与SRS进行比较.各种聚类算法[10]可用于数据划分，包括C-means聚类，模糊C-means聚类和自组织映射(SOM)[11].May等[4]提出基于自组织映射分层采样(SBSS)两步数据分割方法具有很强的稳健性，可以生成更好的人工神经网络模型，比其他技术更有效,在多元和非均匀数据集中更明显.

2 方法

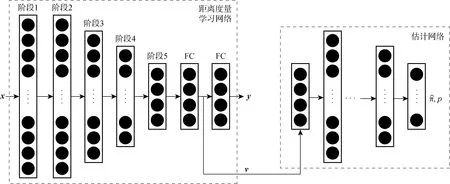
图1 DML-GMM框架Fig.1 Framework of DML-GMM

2.1 距离度量学习网络

距离度量学习问题在机器学习产生时就存在，数据和数据间的相似度差异是可以度量的.因此，距离相近的数据将被视为相似，而相距较远的数据将被视为是不同的[12].样本之间的这种相似性度量需要在一个合理并且可测的空间中进行.May等[4]使用自组织映射方法将原始数据映射到新的嵌入空间，然后通过分层采样对数据进行划分，从而改善训练模型的偏差和方差.Fernndez等[13]通过简单的前馈神经网络将样本转换到嵌入空间，通过计算嵌入空间特征向量的相似度来减少样本冗余并加快训练过程.Baglaeva等[14]通过多层感知机对嵌入空间中的原始数据进行重新划分，建立更精确的空间分布模型，用于模拟城市化地区表层土壤中Cr元素的含量.将样本转换到嵌入空间进行描述有助于更准确地理解样本的特征，并且嵌入空间中样本之间的相似性可以进行度量.受此启发，DML-GMM方法的距离度量学习网络主要分为2个阶段：第1阶段为特征提取，可以使用常见的分类模型进行特征提取；第2阶段为嵌入过程，将提取获得的特征图映射到一个可以度量的空间.该过程包括以下两部分，如图2所示.其中，左侧虚线框图为特征提取模块，可以使用常见的卷积网络提取数据的特征，如ResNet50；右侧虚线框图为特征映射模块，通过两层全连接将提取的特征映射到嵌入高维空间中，进而进行特征转换.第1层全连接层用于输出样本的向量表示，第2层全连接层用于输出预测结果向量.

在基于内容的图像检索和人脸识别等方面获得具有稳健性高且有区分度的特征表示非常重要.但是，在特征学习中通过监督学习的交叉熵损失函数优化并不能学习到足够的区分度，因为其仅注重于找到决策边界以分离不同类别的形状，而没有考虑特征的类内紧凑性[15].为了解决这个问题，目前有许多深度度量学习算法损失函数被提出.首先，介绍两种重要且常用的损失函数：三重损失和中心损失.三重损失在学习特征表示时，将具有相同类别样本点之间的特征距离拉得比具有不同类别样本点之间的特征距离更近.在人脸识别问题中，为了学习更多可鉴别性特征，中心损失被提出作为交叉熵的辅助损失函数一起配合使用.中心损失的主要目标是为每个类别的特征学习一个合适的中心，并将同一类别的样本更紧密地拉到相应的中心.三重损失和中心损失的作用效果如图3所示.由于三重损失处理时需要将数据重新组合，构造起来相对复杂，所以本文借鉴了人脸识别中采用的中心损失来优化以提取特征的距离度量学习网络.该优化过程中同时需要用到样本特征向量表示和输出预测结果，即嵌入过程中第1层全连接的输出v和第2层全连接的输出y(见图2).由此，可以通过中心损失获得更好的样本向量表示，其损失函数Lc可表示为

(1)

式中：czi∈Rd为类zi样本通过网络得到的高维特征向量的向量中心；d为特征维数；f(xi)为样本xi映射的高维向量，f为映射网络；函数D(·)为欧氏距离的平方；N为样本数量.

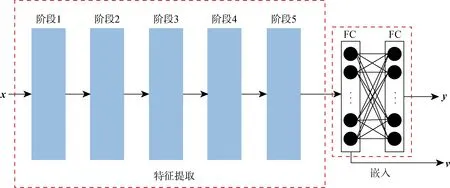
图2 DML-GMM中的DML网络示意图Fig.2 Schematic diagram of DML network in DML-GMM

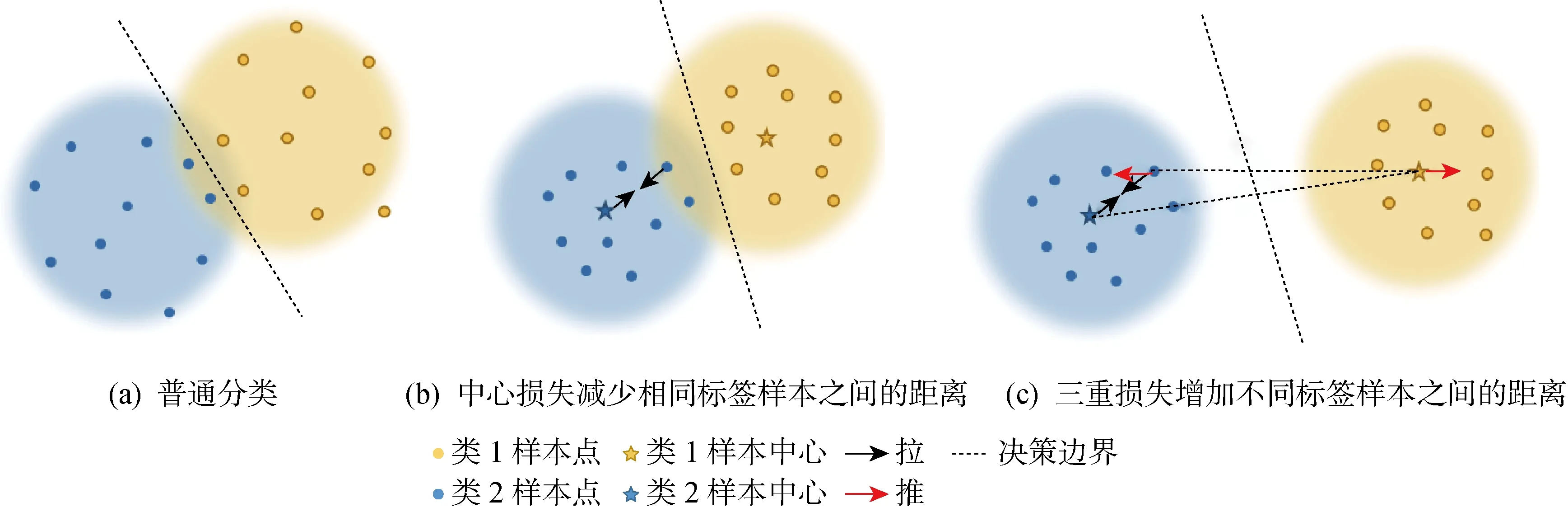
图3 中心损失和三重损失作用示意图Fig.3 Schematic diagram of central loss and triple loss

2.2 基于Gaussian混合模型的分布估计

机器学习算法常常将数据转换到合适的度量空间，然后使用聚类算法来衡量两者之间的相似性.Alonso[16]和Silva等[17]使用 Gaussian混合聚类模型通过对数据进行距离估计来补充缺失数据.还有研究人员将Gaussian混合模型与深度编码器组合在一起，通过深度编码器将样本投射到另一个空间，保留其中异常检测所需的关键信息，将Gaussian混合模型用于估计和检测异常数据[18-20].由于Gaussian混合模型在高维空间中对于样本的分布和相似表示方面具有良好的性能，所以使用Gaussian混合模型来估计样本在高维嵌入空间中的分布.样本的分布特点可以通过其似然概率来描述，然后通过这种分布估计来进行分层采样以获得更好的数据划分.Gaussian混合模型由M个加权Gaussian概率密度函数和所形成的模型，可表示为

(2)

(3)

Gaussian混合模型的估计过程是通过期望最大化(EM)算法实现的，该算法仅能保证到达局部最优点，不能保证该局部最优也是全局最优点.因此，如果算法从不同的初始化点开始优化，容易生成不同的估计.考虑到这种不确定性的情况，对其进行多次拟合，并结合评价指标的平均值和标准偏差来选择合理的参数.这里使用Bayesian信息准则(BIC)来预测实际拥有的数据，此准则可以对Gaussian混合模型拟合的好坏程度进行评估.BIC越低，则用于实际预测的数据(进而扩展到真实的、未知的分布)模型效果就越好[21-22].

3 实验和结果

采用几种不同数据划分方法分别在手写数字数据集MNIST(类似于MNIST数据集的时尚产品图片数据集)、Fashion-MNIST、CIFAR-10这3个开源数据集，以及医院实际采集的临床肺腺癌高分辨率电子计算机断层扫描 (HRCT)图像4个不同的数据集上对于图像分类任务的结果进行比较.上文讨论的各种不同的数据划分方法中，简单随机采样是一种最常用的方法，试错法由于其理论模糊不便于比较，系统采样较难找到一个合理的排序，自组织映射分层采样法相较于DUPLEX法在受到数据分布有显著影响的某些网络上是一种更佳的采样方法[4].因此，本文将比较以下几种数据划分的方法，即SRS、SBSS、DML-GMM.

3.1 实验数据

(1) MNIST：来自美国国家标准与技术研究所(NIST)手写数字开源数据库，该数据包含训练集6×104个示例，测试集1×104个示例，其是NIST数据集合的子集.这些数字已进行尺寸标准化，并在固定尺寸的图像中央.

(2) Fashion-MNIST：Fashion-MNIST数据集是德国Zalando公司提供的服饰图像开源数据集，包含6×104个样本的训练集和1×104个样本的测试集.每个样本都是28像素×28像素的灰度图像，与10个类别的标签相关联.

(3) CIFAR-10：CIFAR-10数据集由10个类的 6×104张32像素×32像素的彩色图像组成的开源数据集，每个类有6×103张图像，有5×104张训练图像和1×104张测试图像.

(4) 肺腺癌HRCT：为了结合实际情况进一步分析数据划分对小样本数据训练的影响，采集来自一家三甲医院的肺腺癌影像临床数据.该HRCT图像一共包含 1 622 个样本的两种类型数据，即715例浸润性肺腺癌CT图像和907例非浸润性腺癌CT图像.

3.2 评价指标

交叉验证是一种用于评估模型的统计方法，也是一个重采样过程，可在有限数量的数据样本上评估学习到的模型.通过计算5折交叉验证的平均准确率、平均方差和平均偏差来比较不同数据分区方法的性能.具体流程如下：

(1) 使用不同的划分方法将数据分为5组；

(2) 进行5折交叉验证，取其中之一作为测试集，并随机选择其余4组中的1组作为验证；

(3) 确定模型训练的终止点，其余3组作为训练集训练模型.

(4)

(5)

(6)

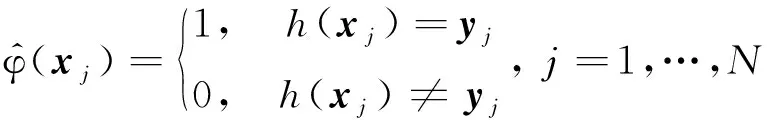
为每个样本分类问题预测输出的正确性，h(xj)为样本的预测标签;yj为样本的标签.

(7)

式中：AUCi为第i次实验中ROC曲线下面积.

3.3 实验步骤

(1) 所有样本放入DML网络中训练50次，并将样本转换为嵌入空间中的高维特征向量.

(2) 数据按SRS、SBSS、DML-GMM 3种不同方法划分，将数据划分为训练集、验证集和测试集以进行模型训练.验证集用于判断模型训练的终点，训练结构完全相同的网络进行比较.

(3) 采用5折交叉验证方法比较训练得到的模型性能指标.

3.4 结果

3.4.1MNIST 对于MNIST数据，SRS方法可以直接通过随机采样的方式划分数据集，而SBSS和DML-GMM方法需要先将样本通过度量网络(6层卷积层和2层全连接层)将样本转换成高维可度量向量，再按照其对应的方法进行数据划分，将重新划分好的数据放入相同的网络中进行训练.由于MNIST数据质量比较高，使用相对较浅层的多层卷积网络就能得到比较好的效果，所以为了更明显地观察出数据划分带来的影响，没有使用特征提取能力更强的网络模型(如ResNet50)来分类效果验证，这里同样仅使用了一个6层卷积层和2层全连接层构成网络来比较分类效果.分别使用3种不同的方法划分数据后，训练结构完全相同的网络，采用5折交叉得到的模型性能指标如图4所示，其在MNIST数据集上的性能对比如表1所示.

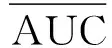
表1 不同方法在MNIST数据集上的性能对比

图4 在MNIST数据集上由5折交叉验证得到的模型性能指标Fig.4 Model performance indicators obtained by 5 folder cross-validation on MNIST dataset

3.4.2Fashion-MNIST 对于Fashion-MNSIT数据集，基于ResNet50模型通过交叉熵损失函数和中心损失函数提取高维特征，再通过两层全连接层将特征转到嵌入空间，分别使用SBSS和DML-GMM方法重新划分样本，对比SRS方法训练相同ResNet50模型得到的模型性能指标如图5所示，其在Fashion-MNIST数据集上的性能对比见表2.

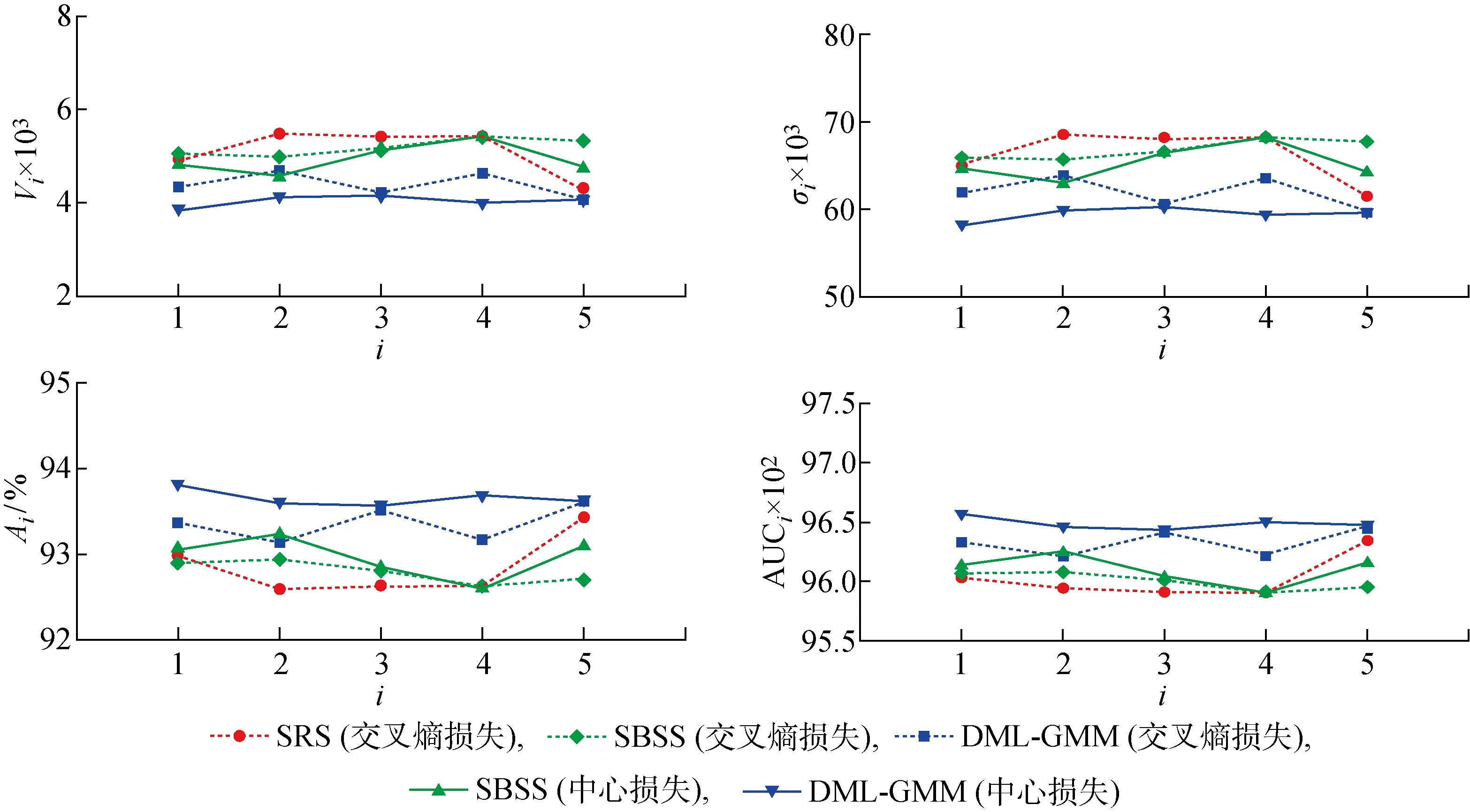
图5 在Fashion-MNIST数据集上由5折交叉验证得到的模型性能指标Fig.5 Model performance indicators obtained by 5 folder cross-validationon on Fashion-MNIST dataset

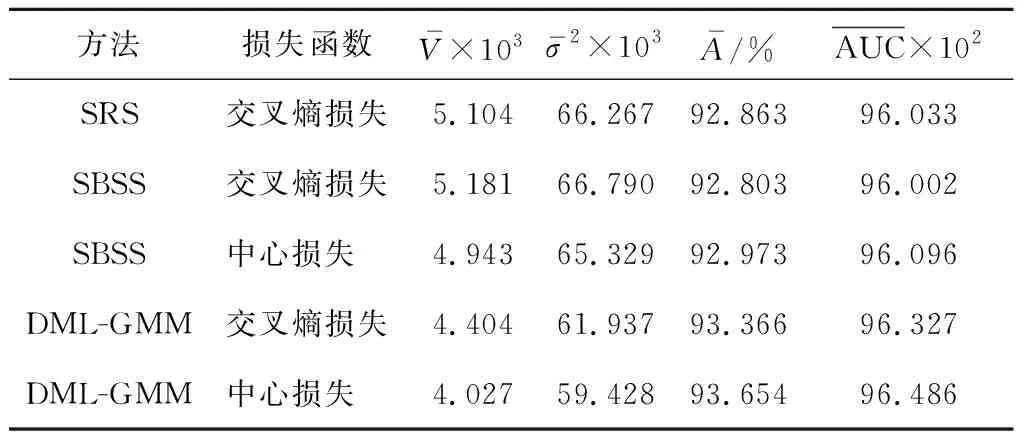
表2 不同方法在Fashion-MNIST数据集上的性能对比

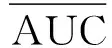
3.4.3CIFAR-10 对于CIFAR-10数据集，使用交叉熵损失函数和中心损失损失函数提取特征，嵌入后分别使用SBSS和DML-GMM方法重新划分样本，对比SRS方法训练相同ResNet50网络得到的模型性能指标如图6所示，其在CIFAR-10数据集上的性能对比如表3所示.由表3可知，在CIFAR-10数据集上，使用交叉熵损失函数提取样本特征嵌入后， 使用SBSS方法划分数据相较于SRS方法训练出来的模型偏差和方差略微小一些，模型性能更好.而使用DML-GMM方法得到的偏差和方差更小，模型性能进一步提升.使用中心损失提取样本特征使用SBSS和DML-GMM方法比交叉熵提取样本特征得到的模型性能进一步有所提高.

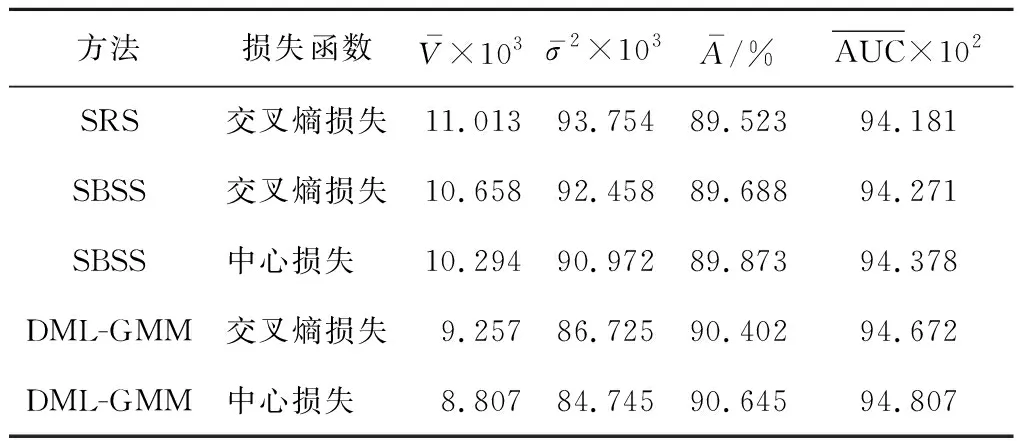
表3 不同方法在CIFAR-10数据集上的性能对比

图6 在CIFAR-10数据集上由5折交叉验证得到的模型性能指标Fig.6 Model performance indicators obtained by 5 folder cross-validationon on CIFAR-10 dataset

3.4.4肺腺癌HRCT 对于肺腺癌HRCT数据集，在提取特征方面使用的是3D ResNet50模型，损失函数分别使用的是交叉熵和中心损失函数，嵌入后分别使用SBSS和DML-GMM方法重新划分样本，对比SRS方法训练相同3D ResNet50模型得到的性能指标如图7所示，其在肺腺癌HRCT数据集上的性能对比如表4所示.由表4可知，在肺腺癌HRCT数据集上，使用交叉熵损失函数提取样本特征嵌入后，使用SBSS方法划分数据相较于SRS方法训练出来的模型偏差和方差略小一些，模型性能更好.而使用DML-GMM方法得到的偏差和方差更小，模型性能进一步提升.使用中心损失提取样本特征使用SBSS和DML-GMM方法比交叉熵提取样本特征得到的模型性能进一步有所提高.

通过上述4个数据集的实验可以看到，在特征提取环节使用中心损失函数相较于交叉熵损失函数可以获得区分度更高的嵌入空间，更加有利于对样本之间差异性的度量.使用SBSS方法划分样本相较于SRS方法中简单的处理样本可以提高训练得到的性能更好、稳定性更佳的模型，而使用DML-GMM方法其模型性能可以进一步获得提升.

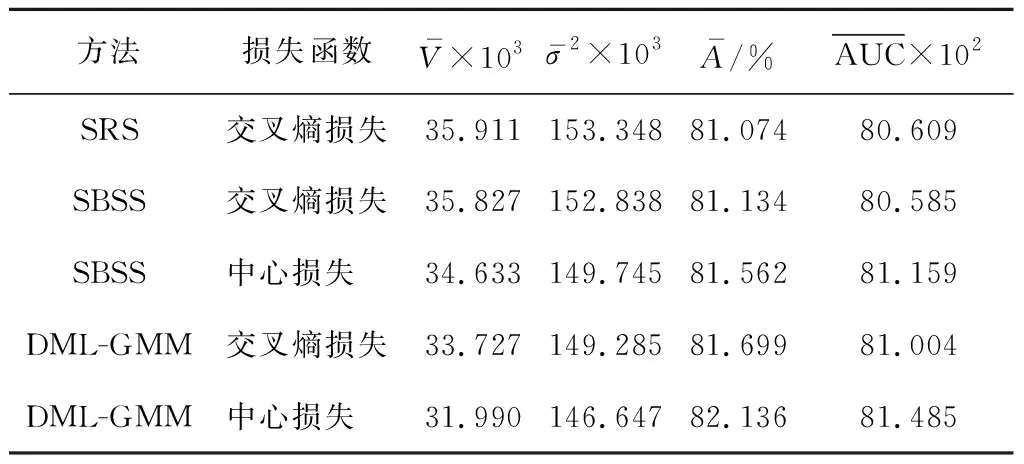
表4 不同方法在肺腺癌HRCT 数据集上的性能对比

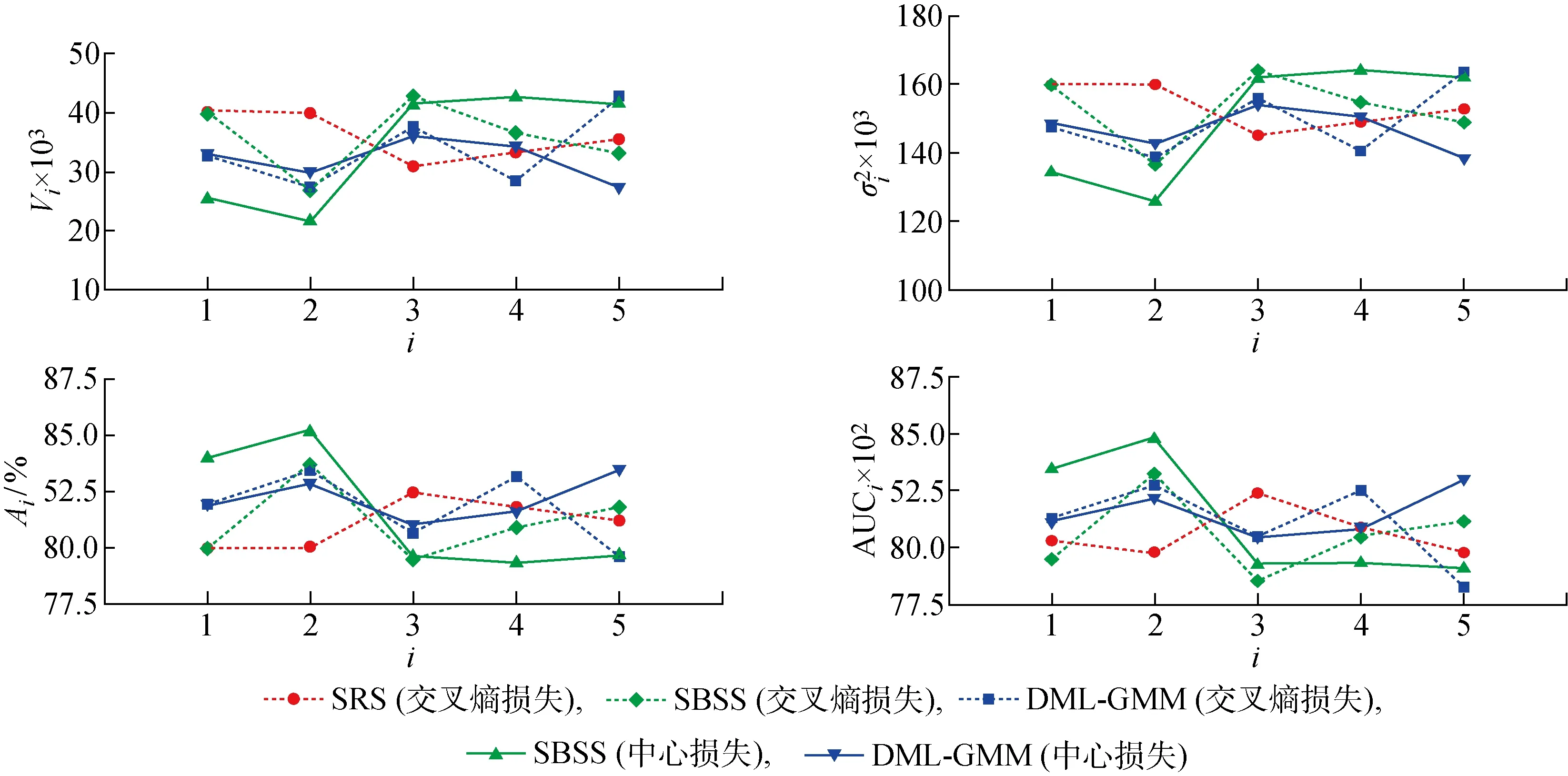
图7 在肺腺癌HRCT数据集上由5折交叉验证得到的模型性能指标Fig.7 Model performance indicators obtained by 5 folder cross-validation on adenocarcinoma HRCT dataset

3.5 稀有样本测试实验

综上，通过使用Gaussian混合模型来估计在嵌入空间中的样本，可计算出每个样本的对数似然，并用其似然概率描述分布特点和样本的典型性，进而发现特征不明显的稀有样本.根据如下步骤进行实验：① 使用SRS方法随机从MNIST数据集中抽取20%作为测试数据，将剩余80%用于训练一个分类网络(6层卷积层和2层全连接层)；② 提取用于训练分类网络的样本向量表示，将其特征的高维向量表示通过Gaussian混合模型描述其样本分布；③ 将测试数据输入训练好的网络，标记出正确分类和错误分类的样本，并放入②中建立好的Gaussian混合模型中计算测试样本的对数似然.所得结果如图8所示，将测试数据中10类对数似然最高和最低的样本显示出来(见图8(a)).由图8可知，对数似然值越高的样本其典型性越高，其特征也越显著、越容易正确分类.样本对数似然值越低其特征显著程度也越低，越不容易分类正确.将具有某一个相同标签的测试数据嵌入到2D空间并用热图对其概率密度进行描述(见图8(b))，可以看到其对数似然值越大，其样本分布在越密集的位置，其对数似然值越低，样本分布在越稀疏的位置.将正确分类和错误分类样本的对数似然用核密度函数描述直方图分布情况(见图8(c)).其中：ρ为样本密度；lnp为对数似然概率.由图8(c)可见，正确分类的样本其 lnp越大，错误分类的样本其 lnp相对更低.因此在实践中，当采集新的样本时，将该样本通过已有样本建立的Gaussian混合模型，计算其 lnp就可以量化样本的显著程度和稀有程度，进而判断是否需对已有模型进行迭代更新，以提高模型的泛化能力.

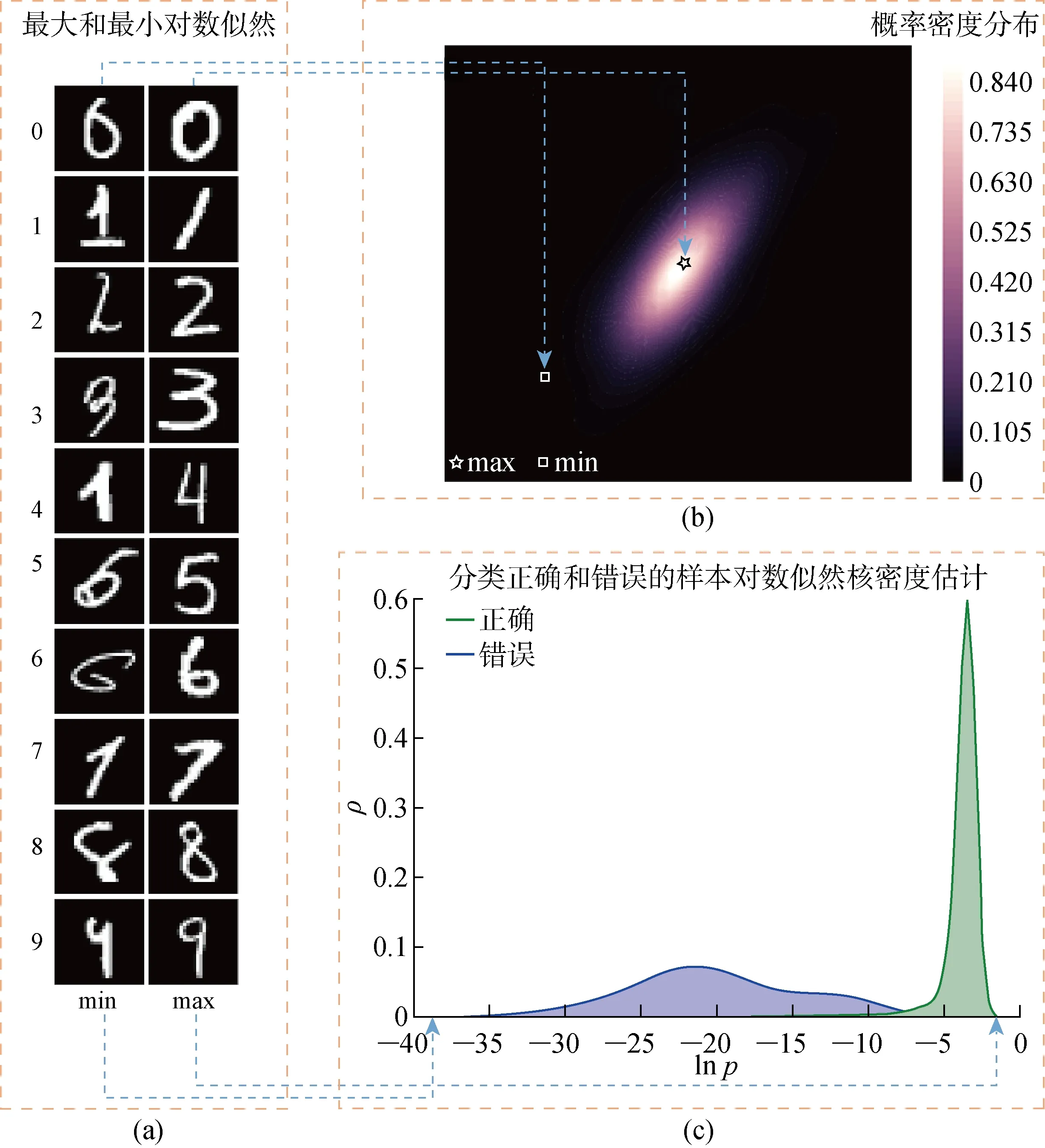
图8 在MNIST数据集上，通过GMM获取的样本对数似然分布及其示意图Fig.8 Log-likelihood distribution and schematic diagram of samples by GMM on MNIST dataset

4 结语

本文提出一种基于Gaussian混合模型的距离度量学习数据集划分方法.首先，将所有样本通过DML网络训练，将样本从图像空间转换到高维特征嵌入空间；然后通过Gaussian混合模型描述其分布后，分层采样划分数据集进行模型训练.通过该方法可以更加准确地了解数据分布的特点，在这样的条件下划分数据相比于其他方法能训练出偏差、方差更小，准确率更高，泛化性能更好的模型.另外，该方法还可以更好地理解样本的显著性，更清楚地了解哪些是最重要的样本，哪些是稀有样本.