基于IHMF算法的火电机组短期负荷预测研究

王力光，封亚钊，王涛，司风琪

(1.大唐环境产业集团股份有限公司特许经营分公司，南京 211100；2.东南大学能源热转换及其过程测控教育部重点实验室，南京 210096)

随着用电结构的升级以及新能源规模化并网所导致的电网随性扰动增加，电网实施了更加精细化的调度，对火电机组等可调可控发电电源的统筹调度也逐渐加强。因此，在深度调峰运行背景下，火电机组负荷经常大幅度变化，而负荷预测将对机组优化运行产生重要影响。

刘卫亮等[1]基于支持向量机构建了锅炉炉膛多层火焰图像和机组负荷之间的关系模型，从而开展了负荷预测。马良玉等[2]分析了影响机组负荷的多种因素，研究各种扰动下机组负荷的变化量，并对负荷进行了预测。刘辉等[3]分析了火电机组负荷控制的特点，提出了一种新的多变量模型预测控制算法。通过小波变换，将负荷序列分解到不同的尺度上分别得到高频和低频序列，对不同子负荷序列分别采用相匹配的模型进行预测，加权求和便可得到完整的负荷预测结果。张然然等[4]耦合自回归积分滑动平均(ARIMA)和小波变换用来进行火电机组负荷的预测。研究结果发现耦合模型的负荷预测精度明显高于ARIMA模型的负荷预测精度。丁伟等[5]提出了一种适用于火电机组负荷预测的历史匹配预测算法(HMF)，该算法的预测精度高于ARMA算法，并且在变负荷过程中优势也较为突出。

负荷预测可分为短期和长期负荷预测两大类。短期负荷预测主要是能够实现未来多个小时内机组发电负荷的预测[6]，目的是为电厂安排日、周调度计划、组合最优机组、协调机组调度、负荷经济分配以及机组优化运行等[7]。本文提出一种改进型的基于历史数据相匹配的机组短期负荷预测方法(Improve History Matching and Forecasting algorithm，IHMF)，基于日负荷的相似性特征，通过加权欧氏距离法同时对负荷的差分序列和原始的负荷序列进行相似性匹配，以归一化后和数值最小为原则，获得最相似日的负荷序列，从而实现对机组短期负荷的预测。

1 基于IHMF的机组短期负荷预测

1.1 HMF机组短期负荷预测算法

基于历史数据匹配的机组短期负荷预测方法(History Matching and Forecasting algorithm，HMF)基于日负荷的相似性特征，对负荷历史数据时间序列进行相似性匹配，得到历史最相似日的负荷变化趋势，依据这些趋势的细节信息实现对未来负荷的预测。将一组负荷数据按时间排序便可得到负荷时间序列，通过加权欧式距离法对不同负荷时间序列进行相似性度量，按式(1)进行计算。

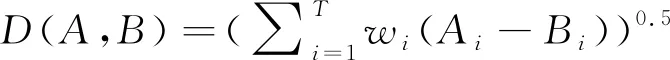
(1)

式(1)中，D为欧式距离，是衡量两负荷时间序列相似程度的一个重要指标；A、B均为负荷时间序列；T为负荷时间序列的长度；N0为常数系数；wi为加权系数，越靠近当前时刻，加权系数越大；λ为加权指数。

HMF算法通过当前时刻t0和历史匹配时长T推算出历史对应时段，并得到对应时段的历史相匹配的负荷时间序列。对历史匹配的负荷时间序列进行差分化处理得到负荷时序变化的一些特征和趋势。进一步地由加权指数λ生成加权系数wi，并基于欧氏距离法进行相似性匹配计算输出最相似日。计算最相似日的负荷变化率，并逐一与当前负荷相乘，最终获得负荷的时序预测值。在训练和测试基于HMF的机组短期负荷预测模型时，通过不断调整历史匹配时长T、加权指数λ，以获得最小的平均负荷预测误差。

以某660 MW燃煤发电机组为例，图1为HMF模型在2020年2月5日17:00～20:00间的机组发电负荷预测结果。图2为HMF模型利用2020年2月5日11:00～17:00的负荷差分数据与历史日同时段的HMF算法匹配的最相似日的负荷曲线。对比图1和图2可以发现，HMF算法通过负荷差分序列进行相似性匹配，虽然可以获得最为相似的负荷变化特征，但却未考虑两者实际负荷的一致性。图1中的历史匹配序列处于高负荷区间，而图2所匹配到的最相似日负荷处于低负荷区间，从而导致负荷预测结果发生偏离。

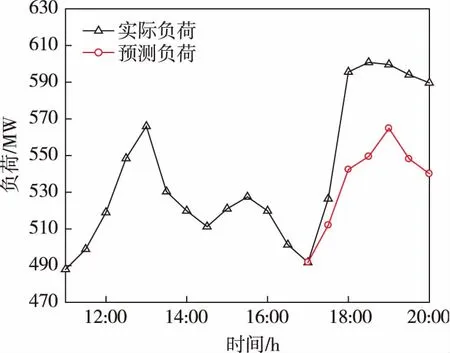
图1 机组发电负荷预测结果

1.2 IHMF机组短期负荷预测方法

由于HMF方法在匹配时间序列的相似性时，通过将历史匹配时间序列进行差分处理，从而利用该差分序列与历史数据中负荷的差分序列进行匹配。该方法只考虑了相邻时刻间负荷的变化量来进行时间序列的相似性匹配，但缺乏对原始负荷序列之间相似性考虑。针对该问题，本文提出了一种改进型的HMF算法，利用欧氏距离法同时对负荷的差分序列和原始的负荷序列进行相似性匹配。随后将两者所得的欧氏距离进行归一化处理后相加，以和最小为原则获得最相似日的负荷序列。IHMF算法的具体计算流程如下：

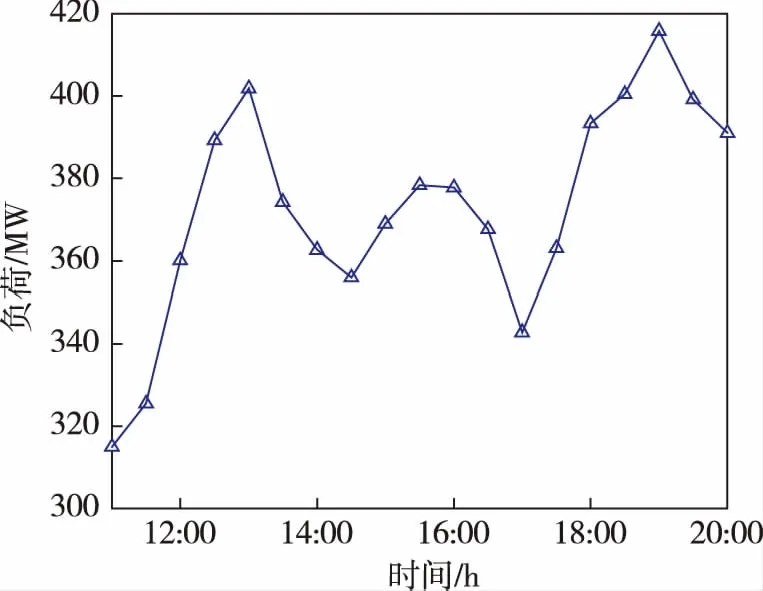
图2 HMF算法匹配的最相似日的负荷曲线

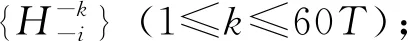
(2)

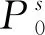
(3)

步骤5：通过式(4)迭代得到预测当天第n时刻的负荷预测值Pn，并获得负荷预测序列。

Pn=Pn-1·ΔPn

(4)

1.3 IHMF模型实例分析以及对比验证

首先从电厂SIS系统中采集该机组自2019年2月15日至2020年2月15日之间的负荷历史数据，取样间隔为1 min。其次利用基于IHMF的短期负荷预测方法进行预测，历史匹配数据为2019年2月15日到2020年2月14日的历史负荷数据，测试数据为2020年2月15日的负荷数据。通过文献[5]确定模型的历史匹配时长T为6 h，加权指数λ为0.15。测试案例中每半小时进行一次预测，合计共48组测试样本，计算各组测试样本的平均预测误差，并且与上文提到的传统HMF算法的预测结果进行对比分析。

某时刻IHMF模型预测曲线见图3。与图1中HMF算法预测精度相比，IHMF算法预测的负荷变化趋势与实际负荷变化趋势吻合更好，表明IHMF算法进行机组短期负荷预测时具有明显的优势。IHMF算法匹配的最相似日的负荷曲线见图4。综合图3和图4中的曲线及数据可知，匹配到的负荷与实际运行负荷所处的区间基本相同，都为高负荷区间，且两者的变化趋势基本一致，因而IHMF算法能够更为较好地预测出未来3 h的负荷。

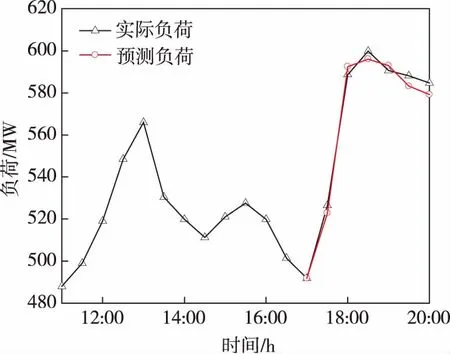
图3 某时刻IHMF模型预测曲线

图4 IHMF算法匹配的最相似日的负荷曲线

表1给出了IHMF算法与HMF算法的预测精度对比。从表1中可以看出，IHMF算法180 min内最大预测误差为6.875%，而HMF算法180 min内最大预测误差达到了12.704%。综合来看，IHMF算法的负荷预测误差时明显小于HMF算法的。因此通过模型对比可知，本文提出的IHMF算法比HMF算法具有更好的负荷预测效果。

表1 IHMF算法与HMF算法的预测精度对比

除此之外，本文还对2020年2月15日到2020年2月18日连续三天的机组负荷进行了预测，依然按照原先的方案即每半小时预测一次，每次预测未来三小时的负荷。IHMF模型连续三天机组负荷预测结果见图5，从图5中可以看出，实际负荷曲线与IHMF模型给出的预测负荷曲线几何重合，拟合优度R2达到了0.913 4，即表明IHMF模型在长时间的连续预测状态下也能给出较好的预测结果。将负荷预测结果与实际负荷对比可知，IHMF模型的平均预测误差仅为13.36 MW，体现了IHMF模型拥有很高的负荷预测精度，可有效应用于电站实际生产，方便运行人员依据负荷预测结果提前制定机组运行计划与生产方案。

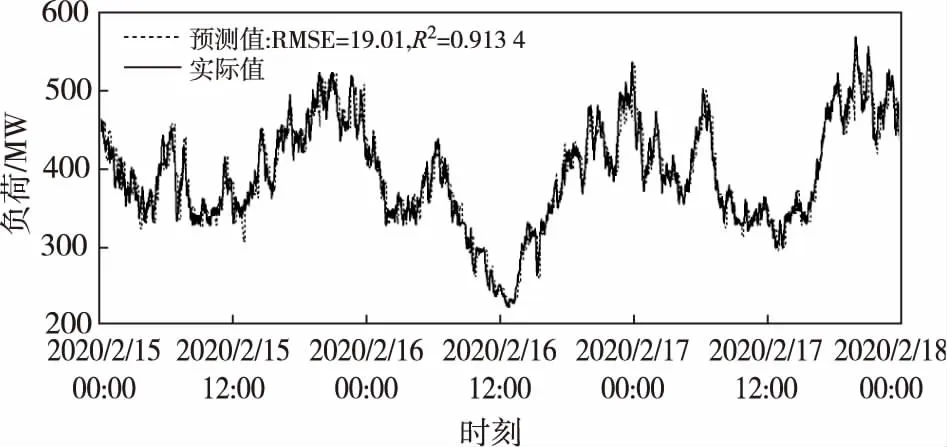
图5 IHMF模型连续三天机组负荷预测结果

2 结语

本文提出了一种基于IHMF算法的机组短期负荷预测模型。基于日负荷的相似性特征，通过加权欧氏距离法同时对负荷的差分序列和原始的负荷序列进行相似性匹配，基于归一化后的和最小原则获得最相似日的负荷序列。研究发现IHMF模型在较长时间的连续状态下均能够较好地预测出未来负荷的变化，并且相比传统的HMF预测模型有着更高的预测精度。