内嵌树状流道的薄片结构流-热-力特性分析

Saadat Fatima，Hashmi Abdul Rehman，朱磊磊

(1.南京理工大学能源与动力工程学院，南京 210094；2.浙江大学能源工程学院，杭州 310027)

点-体流动过程在工程界和自然界十分常见，所谓点-体流动是指由一个点向一个体积区域输送流体。为了提高输送效率，通常在该体积区域内嵌流道，流道区流阻较小，其体积可代表输送流体的投资成本，非流道区一般是功能区，流体主要通过渗透传输，流阻较大。流道区体积越大，总输送流阻和耗功越小，但对应的功能区体积也越小，因此二者之间存在权衡关系。在给定流道体积时，流道结构有均匀流道(单一尺度流道)和多尺度流道两类，经过优化的多尺度流道在很多情况下要优于均匀流道，因此多尺度流道的设计引起了普遍重视。在多尺度流道设计时，有两种常见结构：树状流道和网状流道。网状流道在流道局部出现堵塞等非设计工况时，仍能维持较好的性能，即可靠性较高[1]。树状流道在可靠性方面不及网状流道，但因其流道体积利用率高，在微电子冷却、燃料电池流场设计和流体分布器等多种工程应用中引起了普遍关注[2-7]。

早期对树状流道的代表性研究是Murray做出的[8]，其结果后来被命名为Murray定律，该定律建立了树状流道层流流动时的优化直径比。Bejan及其合作者系统研究了树状流道在电子器件散热、流动分配器等多方面的应用，其所提出的构形理论激发了大量的有关树状流道在传热传质等领域的研究。Bejan和Errera[9]对多孔介质的点-体传质问题进行了研究，优化了多孔介质中高渗透率材料(或间隙)的结构，结果表明优化的树状结构较之均匀结构性能更佳。Chen等[10]采用达西流和哈根-泊肃叶流模型研究了面-点流动过程，对一级分叉结构给出了均匀流道和树状流道两种设计何者占优的判别条件。本文在前人流动优化的基础上[9-10]，研究内嵌树状流道的薄片结构的流-热-力特性和非设计工况特性，为工程设计优化提供参考。

1 几何模型

1.1 设计工况

图1给出了内嵌流道的扇形薄片结构示意图，此图以二维为例，如果是三维结构，流道为圆管，其直径最大不超过薄片厚度，薄片厚度则远小于扇形直径。图1(a)采用均匀流道(直径数n=1)，流道数m=5只是举例，其优化值由设计决定；图1(b)采用树状流道，为简便起见，本文仅讨论只有一级分叉的情况(直径数n=2)，此时树状流道相当于Y形流道，树数m=3也只是举例，其优化值也由设计决定。流道区以外的区域假设为多孔介质区(即功能区)。流体从扇形根部流入，在流道区(低阻区)和多孔介质区(高阻区)内流动，最终在整个区域沿垂直于区域面积的方向(令其为法向)流出。在分析耐热和承载能力时，沿法向有外加热流输入薄片，同时薄片承受外加的均匀载荷。

流道体积是流体输送的投资成本，定义流道体积比φ为流道体积Vf与整个薄片体积V之比：

(1)

对于二维情况，流道体积比变为流道面积比，即流道面积Af与整个薄片表面积A之比：

图1 内嵌流道的扇形薄片结构

(2)

对于树状结构，当n= 2时，定义流道直径比β和长度比γ分别为：

(3)

(4)

式(3)和式(4)中，d1和d2分别为树状上下游两级流道的直径，l1和l2分别为树状上下游两级流道的长度。

1.2 非设计条件

树状流道的一个主要缺陷是当流道某处出现阻塞等非设计条件时，其下游的流体输送将受到较大影响。图2给出了各种可能的阻塞位置，其中图2(a)和图2(b)中阻塞发生于流道中，图2(c)和图2(d)阻塞发生于功能区。很显然，发生流动入口处的阻塞(即A1和B1)影响最大，本文仅以A1和B1为例。对于二维设计，取A1和B1充满入口流道界面，其阻塞面积为1.92 mm2。

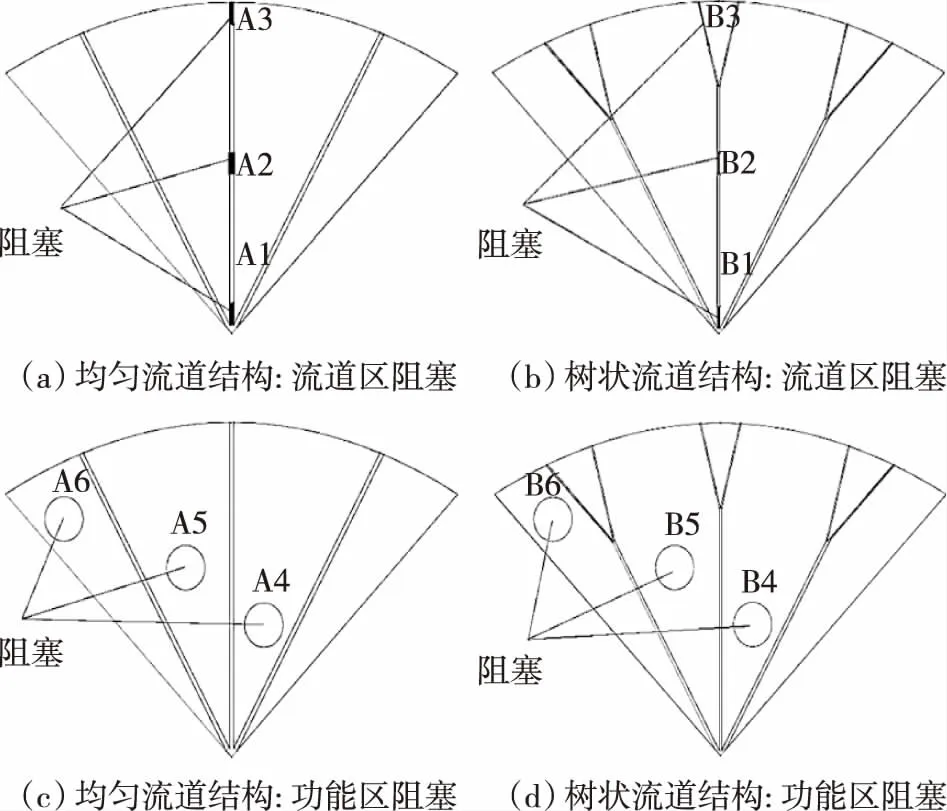
图2 各种可能的阻塞位置

2 数值模型

2.1 流动传热模型

假设流体(水)输送过程包括流道区的稳态层流和功能区的多孔介质内达西流。流道区流体的连续性方程、动量方程和能量方程分别为：

(5)

(6)

(7)

(8)

(9)

功能区采用多孔介质模型，其具体方程细节可见多孔介质流动传热相关文献，如文献[11]或数值模拟软件手册文献[12]。流动传热模型的边界条件为：扇形区域根部入口流量为1.182 9 ×10-6kg·m/s，入口温度为300 K，外缘出口压力为0 Pa(表压力)，上表面热流密度为1 000 W/m2，底面和外缘绝热。固体热物性为密度700 kg/m3，比热为2 310 J/(kg·K)，导热系数0.173 W/(m·K)。

以上流动传热模型采用基于压力-速度耦合算法的商用软件ANSYS Fluent求解[12]，求解时连续方程和动量方程的残差取为10-4，能量方程的残差取为10-6，相邻网格计算结果相差最大不超过1%，对于不同的算例网格单元数从几百万到一千多万不等。为了评价流体输送和耐热性能，取最大压降ΔPmax和最高温度Tmax作为指标，显然，ΔPmax和Tmax越小，性能越好。

2.2 应力应变模型

为了分析流道设计对薄片结构承载能力的影响，建立应力应变模型。假设薄片表面承受均匀静态载荷，功能区近似为纯固体结构，变形为小量。详细的应力应变模型方程可见材料力学文献或数值模拟软件手册，如文献[13]。应力应变模型的边界条件为：流道入口处为固定点，薄片顶面压力为10 Pa。除热物性外的其它物性包括泊松比为0.33，杨氏模量为50，体积弹性模量为4.90×107Pa，剪切模量为1.87×107Pa。网格独立性校核时，相邻网格计算结果相差最大不超过1%。

本文采用商用软件ANSYS Workbench[13]的静态结构分析功能计算应力应变，应力计算结果采用von Mises应力表示，即：

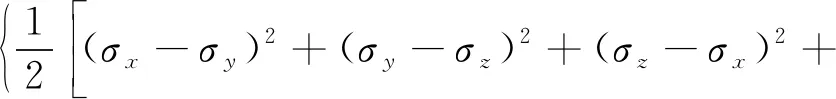
(10)

为了比较采用均匀流道和树状流道的两种薄片的承载能力，采用最大应力σmax和最大变形δmax作为指标，显然，σmax和δmax越小越好。

3 结果和讨论

3.1 二维流动优化特性

表1给出了均匀流道(φ=5%，n=1)和树状流道(φ=5%，n=2，β=γ=0.5)的最大压降。当流道数m为3时，两种流道的最大压降均存在最小值，且树状流道的最大压降最小值更低，这说明树状流道流阻更小，在输送同样流量时耗功更小、更节能。二维流动优化简单易行，其结果(m=3)可近似用于三维结构性能分析。

表1 均匀流道和树状流道最大压降对比

3.2 三维传热特性

基于二维流道优化结果(m=3，β=γ=0.5)，图3给出了三维结构设计条件下最大压降和最高温度(图中ψ为功能区孔隙率)。由图3可知，在给定条件下，树状流道最大压降显著低于均匀流道，树状流道的最高温度低于均匀流道，说明树状流道不仅具有更小的流阻，也同时具有更强的传热性能。事实上，在均匀流道下游区域的中间位置，流道的影响距离较远，而树状流道则可以在整个区域更好地分配流阻和热阻，从而使得最大流阻和最高温度下降。三维结构中间厚度处截面温度场见图4，由图4可见，二者分布特性差异较大，树状流道的高温区(接近最高温度的区域)较少。

薄片中出现阻塞时对流道和传热会产生影响，显然阻塞发生于薄片根部流道时(例如A1，B1)影响最大。图5为阻塞分别产生于A1和B1时三维结构最大压降和最高温度。与图3相比，对均匀流道和树状流道，阻塞均导致流阻显著增大，对于均匀流道最高温度变化轻微，对于树状流道，阻塞导致最高温度有一定升高(即传热能力下降，不利于散热)。

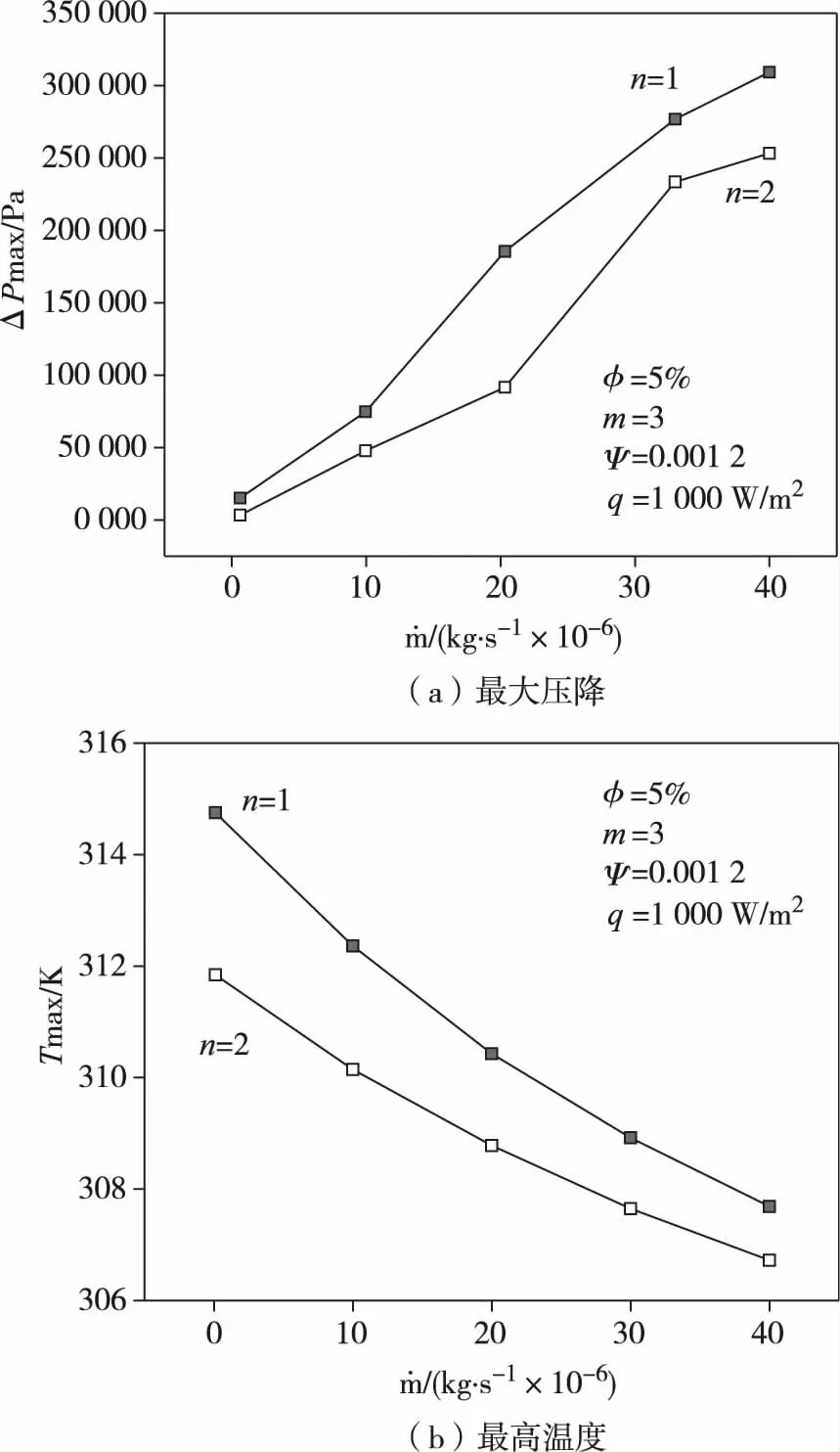
图3 三维结构设计条件下最大压降和最高温度

3.3 应力应变特性

表2给出了在优化流道设计条件下的最大应力σmax和最大应变δmax的计算结果，对于均匀流道(φ=5%，n=1，m=3)；对于树状流道(φ=5%，n=2，m=3，β=γ=0.5)。由表2可见，无论有无阻塞，树状流道结构的最大应力和最大变形均明显低于相应的均匀流道，这说明树状流道具有更好的承载能力；在A1和B1有阻塞时，无论树状流道结构还是均匀流道结构，最大应力和最大应变均低于相应的无阻塞工况，这是因为阻塞使得流道空间变为固体，增强了薄片结构的强度和承载能力。

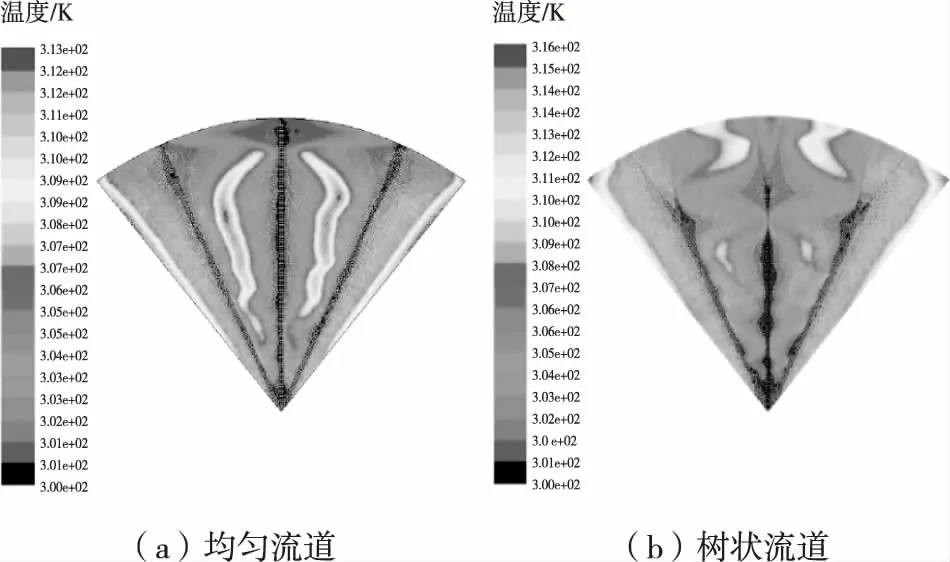
图4 三维结构中间厚度处截面温度场

图5 阻塞分别产生于A1和B1时三维结构最大压降和最高温度

表2 优化流道设计条件下的最大应力和最大应变

4 结语

1)薄片结构内嵌流道用于流体输运和传热时，优化的树状结构比均匀结构流阻更低、耗功更小，同时传热能力和承载能力也更强，即树状流道结构在流-热-力性能三方面均优于均匀流道结构。

2)当薄片结构出现根部阻塞时，与无阻塞工况相比，均匀结构和树状结构的流阻均显著增大，且阻塞对树状流道传热能力(最高温度)的影响更大些，最大应力和最大变形则均减小。