基于改进灰狼算法的电网主变负载自动风险评估模型

范强，吕黔苏，万金金，肖宁，肖书舟，张迅，古庭赟

(1.贵州电网有限责任公司电力科学研究院，贵州 贵阳，550002；2.贵州创星电力科学研究院有限责任公司，贵州 贵阳，550002；3.贵州电网有限责任公司，贵州 贵阳，550002)

电网用电负荷逐年增加，当处于用电高峰或环境恶劣时，电网容易发生各种突发性故障，导致频繁停电和严重伤亡。因此，对电网主变压器的负荷风险进行评估是非常重要的[1]。

针对上述问题，文献[2]根据遗传算法的功能特点，设计了全新的风险评估模型。该模型全方位实时监控系统，利用粗糙集和分辨函数求解最优结果，完成风险评估。但该模型由于评估过程较为复杂，很难评估所有风险数据。文献[3]研究的风险评估模型，预先归纳了不同的故障类型，然后从系统保护层信息流和物理电网能量流两个角度，建立能够自动评估风险的方法。但该模型对风险数据的搜索模式较为烦琐，导致风险评估结果不够准确可靠。文献[4]提出了配电网馈线负载预测及风险预警模型，分析电网历史负载特性，采用聚类法细分负载类别，进行负载分布预测，评估馈线负载风险并进行预警，该方法通过历史数据预测负载风险，在实际负载风险评估过程中效果不佳，不能评估所有风险。

基于以上研究成果与不足，进一步提高风险评估结果的可靠性，此次研究利用改进灰狼算法进行创新，提出基于改进灰狼算法的电网主变负载自动风险评估模型，改进灰狼算法是对基本灰狼算法的改进，加强算法自身的搜索能力和迭代能力，为电网相关领域的风险评估提供更加有效的技术。

1 基于改进灰狼算法计算主变负载因子

1.1 设置关联数据挖掘规则

自动化获取电网主变负载风险节点，需要依靠可靠的规则，因此，在预先获得基本监测数据的基础上，设置关联数据挖掘规则，依靠有序的规则找出各个节点数据之间的关联性。

已知目前大多数数据库只具备录入、查询等基本功能，单纯地存储数据无法发现其中包含的有用信息，因此，利用Apriori-algorithm技术，设置模型的关联数据挖掘规则。假设数据库中存在两个不同的集合，分别为集合U和集合V，则两项事件同时发生的概率，就可以默认为数据关联规则的相对支持度，公式为：

support(U=≥V)=P(U∩V)

(1)

当集合U发生变化时，则集合V发生的概率，可以表示数据关联规则的置信度，即存在：

confidence(U=≥V)=P(V|U)

(2)

而数据库中的项集可以分为两个大类，分别为频繁项集和非频繁项集，因此在设置挖掘规则时[5]，需要针对不同属性的项集区分挖掘方式。利用选择的Apriori-algorithm技术，找出数据库中的所有频繁项集，筛选其中的最大频繁项集Wmax。图1为Apriori-algorithm技术下获得的频繁项集与非频繁项集。

图1 频繁项集与非频繁项集示意图Fig.1 Schematic diagram of frequent itemsets and infrequent itemsets

需要遵循上述设置的关联数据挖掘规则，获取影响电网主变负载的因素。

1.2 改进灰狼算法搜索主变负载影响因素

按照设置的挖掘规则，采用改进灰狼算法搜索主变负载影响因素。

该算法以独立的灰狼个体为基础，划分两种不同的搜索模式：跟踪搜索和自主搜索。因此假设每头狼都能使用跟踪搜索和自主搜索模式；每头狼都按照设置的关联数据挖掘规则，确定自身的搜索模式。当狼群采用跟踪搜索模式时，依据原始灰狼算法更新灰狼个体位置，指引自己进入最优解区域；当狼群采用自主探索模式时，此时该算法获取等级高于自身和自身的所在位置信息，同时以随机变向的方式[6-7]，实时更新自身位置。

由于灰狼算法会根据自身的等级来转换搜索模式，为此，本文改进的灰狼算法通过上述四组位置更新规则，搜索主变负载影响因素，也就是说，按主变负载影响因素适应度值的优劣，为构建自动风险评估模型提供原始数据，将候选解按照4个等级进行划分，其中最优解记为a，且该解的等级为1；次优解记为b，该解的等级为2；第三优的解记为c，等级为3；最后的选解为d，设置其等级为4。假设算法共使用了i头狼，则当搜索时间为t时，第i头狼的等级为wi(t)，则存在下列方程组：

wi(t)=1,wi(t)=2,wi(t)=3,wi(t)=4

(3)

上述四组计算公式，分别表示t时刻下，第i头狼在群体中的所属等级为分别为1级、2级、3级以及4级。利用决策因子QFi(t)标记所有灰狼个体的等级，则：

(4)

公式中：D表示狼群的总等级，也就是4。根据上述公式可知，当灰狼的等级为1时，则决策因子的值同样为1；当灰狼等级为2时，则决策因子的值为0.67；当灰狼等级分别为3和4时，此时的决策因子分别为0.33和0。在算法的整个迭代任务中，一个候选解都会都存在一个随机数λ0，该值的取值范围在(0,1)之间。当存在λ0≤QGi(t)的条件时，该算法在第t时刻就会转换成自主探索模式[8-11]，若不满足上述条件，则算法会一直维持跟踪搜索模式。由于λ0的值恒小于或等于1，所以a灰狼只能采用自主探索模式；而d灰狼的决策因子为0，所以d灰狼只能采用跟踪搜索模式。针对上述分析设置不同等级灰狼的位置更新方式，其中a灰狼的位置更新通过下列公式实现：

(5)

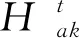
(6)

(7)

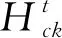
(8)

公式中：H3s来源于公式(7)，即t与n为3时。依次迭代，可获取灰狼的实时位置。

1.3 计算负载相关因子

根据获得的主变负载影响因素发现，电网在主变重载以及过载过程中，会出现告警或故障现象，因此模型为了监测主变负载风险的变化情况[12-16]，计算各个负载相关因子。负载相关因子的计算公式如下：

F=∏ifi

(9)

公式中：F表示负载相关因子；fi表示不同的因子类型，包括老化因子、缺陷因子、告警因子、历史重载以及过载因子等。当电网主变设备投运年限不断增加时，老化因子的取值可按照0～5年、5～10年、10～20年、20～30年以及30年以上进行划分。

缺陷因子产生于本体、绕组、铁芯、箱壳等与电网设备相关的部位，不同的缺陷表象，可根据一般、重大、紧急、其他四个类别，划分为不同的缺陷等级；告警因子主要包括油色谱、油温和绕温等[17-19]，其中油色谱可以通过四比值法获得，产生此项告警的原因包括正常劣化、导线过热、悬浮电位引起的连续火花、绕组环流、有工频续流的闪络以及局部放电等；而导致油温和绕温告警因子各包括四类，分比为上层油温、绕温低于85℃；上层油温、绕温大于等于85℃小于95℃；上层油温、绕温大于等于95℃小于105℃；上层油温、绕温大于等于105℃；历史重载以及过载因子是过去发生的影响因子值，按照不同的统计数据，可划分成历史过载总次数小于50、历史平均负载率小于40%；历史过载总次数大于等于50小于200、历史平均负载率大于等于40%小于60%；以及历史过载总次数大于等于200、历史平均负载率大于等于60%，以此类推划分负载率等级。利用公式(9)计算上述提到的负载相关因子，为构建评估模型提供衡量指标[20-24]。

2 基于负载相关因子的自动化风险评估模型

已知电网主变负载事件发生概率，与造成的严重程度，是模型评价风险的基本要素[25]，而两个参数的乘积就是评价事件风险的指标，模型根据指标自动化评价电网的安全性[26-27]。因此假设事件风险指标为Risk，风险事件发生的概率以及导致的后果严重程度分别为Probability和Severity，则风险指标的取值通过下列公式获得：

Risk=Probability×Severity

(10)

而其中的Probability作为负载风险发生的概率，可通过下列计算公式获得：

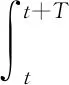
(11)

公式中：T表示主变负载率的时间区间；β(t)表示t时点的负载率，Ft表示t时点的相关负载因子。根据RBSA(基于风险理论的电力系统安全评估方法)的研究成果可知，构建的评估模型需要具备如下性能：均衡分析安全性、指示电网工作系统状态、组合风险、累加风险。因此，综合考虑上述分析结果，根据负载风险发生概率Probability，构建自动化风险评估模型：

(12)

公式中：Xt、Xt+1分别表示t时刻以及下一时刻，电网系统的运行状态；Ei表示可能发生的第i个事件。根据模型得到的风险值评估结果R(Xt)，确定电网主变负载风险程度[28-29]。至此，基于改进灰狼算法，实现电网主变负载自动风险评估模型的构建。

3 仿真实验

3.1 算法测试

为了验证改进灰狼算法在电网主变负载自动风险评估模型中的稳定性，以某供电局110kV某变电站电网主变电器#1变压器为例，评估其2021年8月份的负载风险值，其96点时间序列的负载率数据，数据样例如图2：

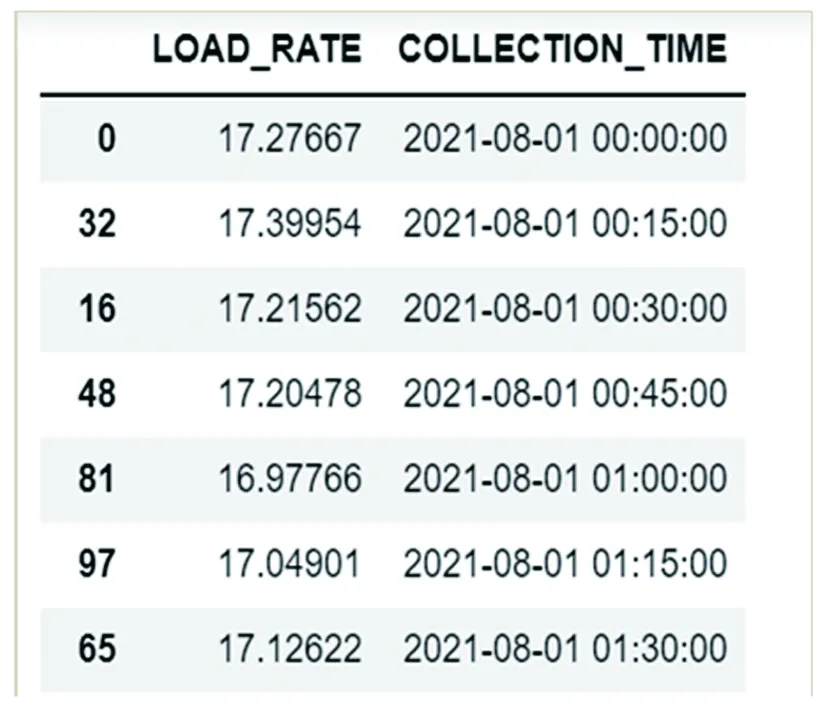
图2 负载率时间序列数据Fig.2 Load rate time series data

设备缺陷将影响主变负载风险值，因此需要查询#1主变当前所有未消缺的缺陷数据1条，数据如表1所示：

表1 主变实际未消缺数据Tab.1 Actual uncancelled data of main transformer

该主变的计算风险值R为49.54，各负载风险因子值如表2：

表2 负载风险因子值Tab.2 Load riskfactor value

根据表2综合考虑该设备的风险特点，投运年限较长，存在未消缺的缺陷，低水平运行风险值处于正常范围，但在运行过程中应重点关注其负载变化，可能会由于负载变大导致风险快速升高。

基于以上实际数据，通过6组电网主变负载风险测试函数，检验改进灰狼算法与灰狼算法、三组常规模型算法(文献[2]模型、文献[3]模型、文献[4]模型)之间的差异性。设置文中模型算法为实验组，三组常规模型算法分别为对照A组、B组以及C组，灰狼算法模型为D组。为了防止测试结果存在唯一性，让五组算法分别运行50次，计算平均值得到如下表3、表4、表5、表6及表7所示的测试结果。

表3 改进灰狼算法函数测试结果Tab.3 Test result of improved gray wolf algorithm function

表4 对照A组算法函数测试结果Tab.4 Compared with the test result of Group A algorithm function

表5 对照B组算法函数测试结果Tab.5 Compared with the test result of Group B algorithm function

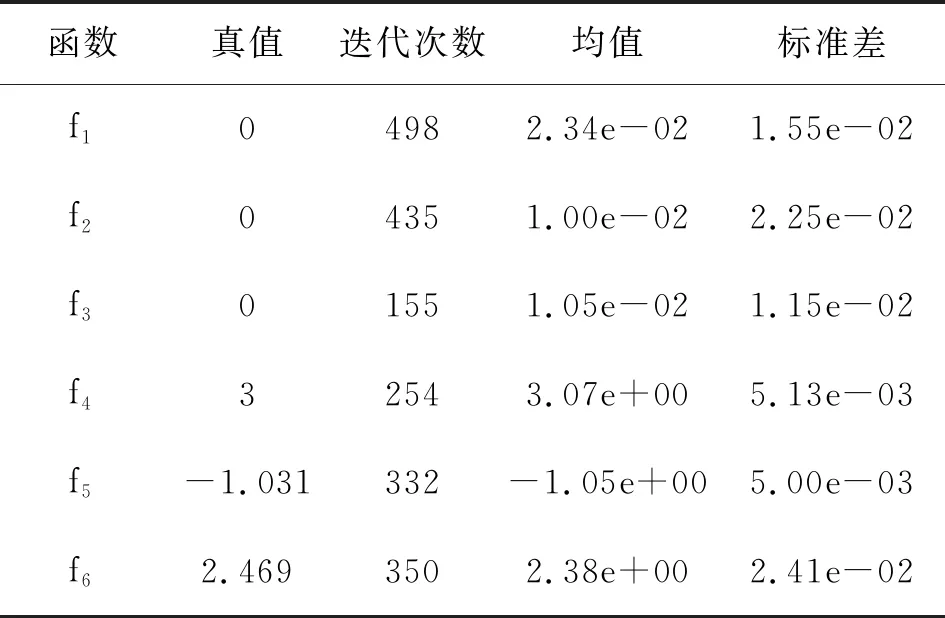
表6 对照C组算法函数测试结果Tab.6 Control Group C algorithm function test results

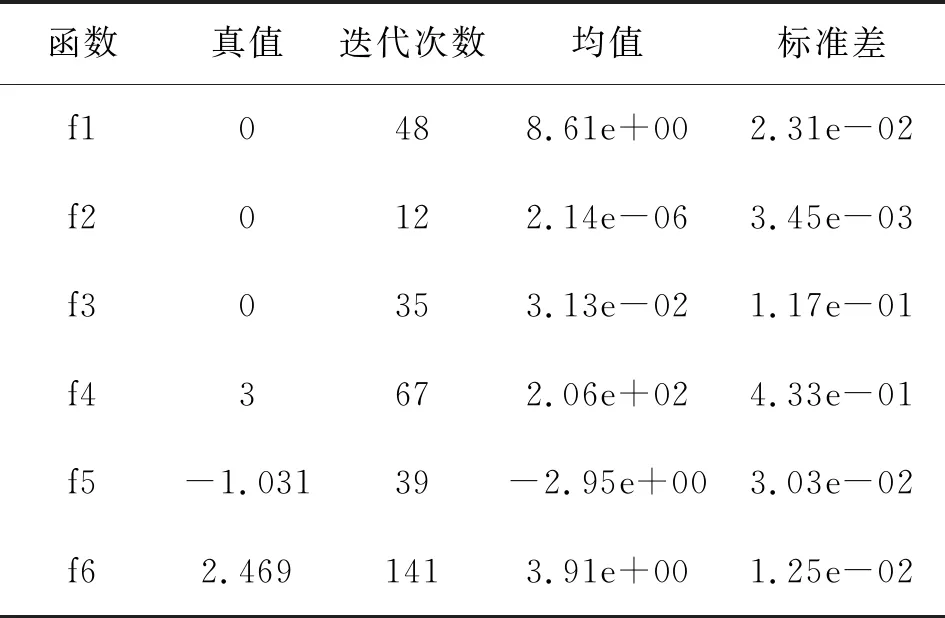
表7 对照D组算法函数测试结果Tab.7 Compared with the test result of D group algorithm function

根据表4-表7中显示的测试结果可知，五组算法均可以解决有约束条件和无约束条件的问题。与对照A组、对照D组和对照C组模型算法相比，对照B组模型算法的均值，更接近测试函数真值，且准差上更小，平均迭代次数最少。根据不同测试数据可知，对照组模型算法容易陷入局部极值，而根据表3中改进灰狼算法函数测试结果可知，该算法与其他四组模型算法相比，该算法的收敛速度更快、更稳定，且不容易出现局部极值的情况。

3.2 搜索路径测试

根据上述分析结果，在同样的测试环境中，利用四组模型搜索某供电局110kV电网主变负载风险数据。

利用现有的实际栅格模型，构建一个规格为10*10的测试环境，一共有100个独立的小栅格。设置每个栅格的边长均为1，保证独立小栅格规格完全相同后，设置每一个小栅格的编号，按照1～100的顺序排列。实验测试任务在下图3所示的环境中进行。

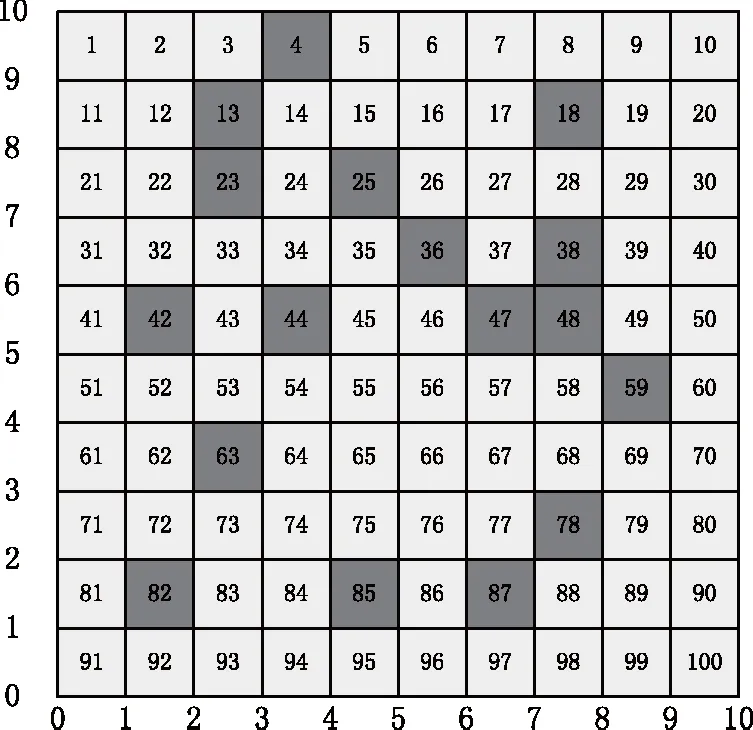
图3 实验测试环境Fig.3 Experimental test environment

负载风险评估模型基于对异常负载数据的搜索，因为异常负载即是风险，搜索出异常数据，即为评估电网风险。因此验证五组模型的负载风险评估效果，可以通过对异常负载风险数据的搜索效果体现。为了便于比较搜索线路与影响因子，对负载风险评估模型评估效果的影响，测试环境中利用浅色栅格表示电网所有正常主变负载数据，利用深色栅格表示异常负载数据。分别利用五组模型搜索图3中的异常负载数据，以评估负载风险，得到的测试结果，如图4所示。

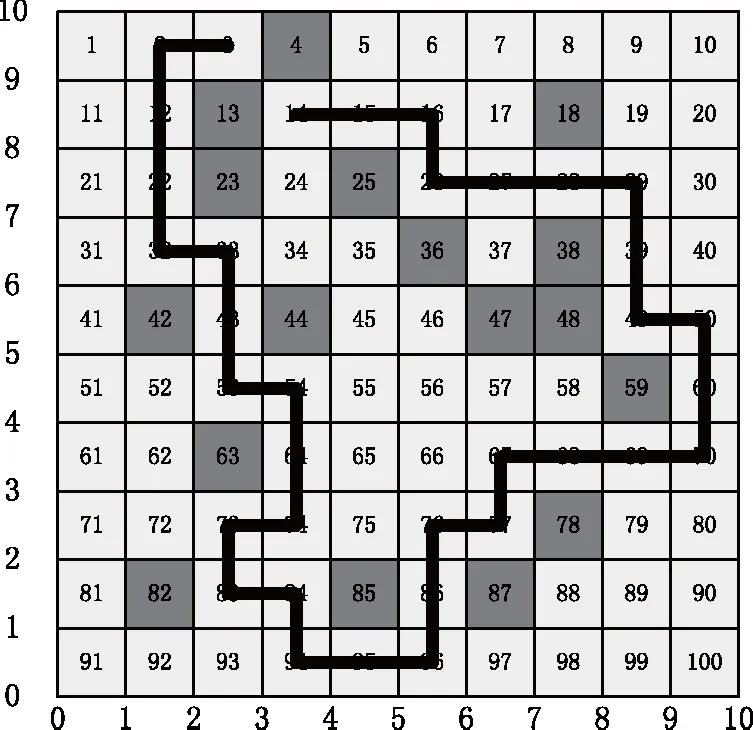
(a)实验组(a) Experimental group

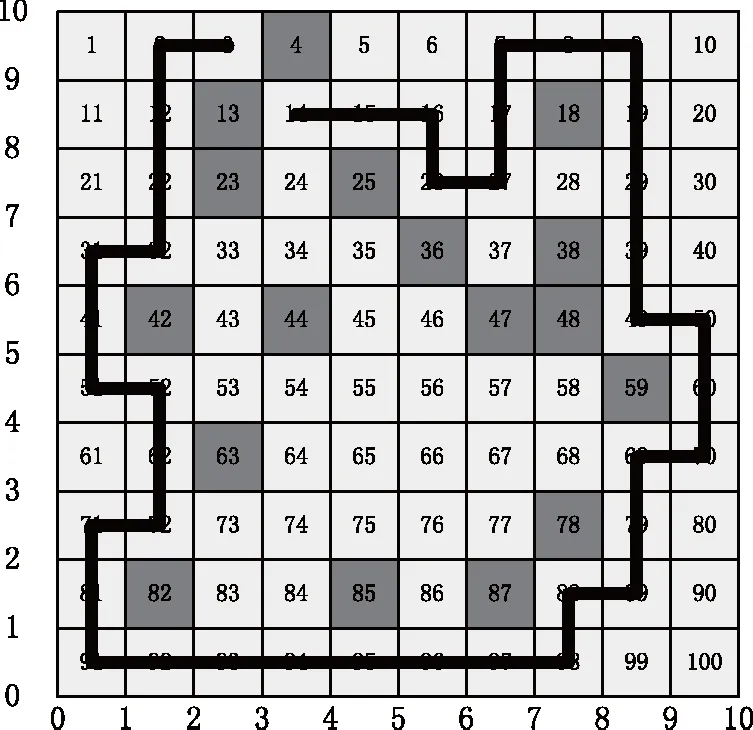
(c)对照B组(c) Reference group B

(d)对照C组(d) Reference group C

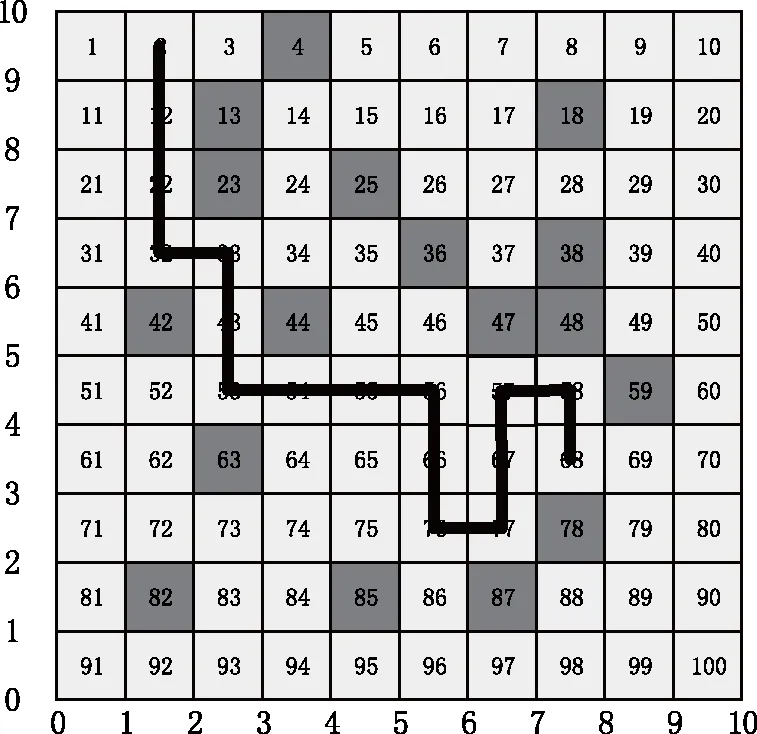
(e)对照D组(e) Reference group D图4 模型搜索路径对比Fig.4 Model search path comparison

根据图4显示的测试结果可知，面对同样的测试环境时，实验组模型搜索到了每一个异常栅格；综合上述实验测试结果，可以看出，对照A组、对照C组、对照D组模型只得到了部分存在风险的栅格；对照B组模型尽管扩大了搜索范围，但并没有获得全部存在风险的栅格。

基于灰狼改进算法的模型，自动化评价风险时，能够获得电网主变负载全部异常数据，即获得电网主变的全部负载风险，证明了模型风险评估的有效性。而其他三组模型的搜索线路不是最优，导致风险评估结果受到影响。

4 结束语

此次研究利用改进灰狼算法加强模型自动化搜索能力，根据相对支持度和置信度建立关联数据挖掘规则。基于改进的灰狼算法，设置跟踪搜索和独立搜索两种模式，计算相关负荷因素，定义风险指标以完成自动风险评估，其评估过程的收敛速度更快更稳定，且不容易出现局部极值的情况，且搜索到了每一个异常栅格，为风险评估提供更加可靠的数据。

所提方法针对数据质量、多源数据融合等问题，该方法没有过多说明，因此在使用该模型评估电网主变负载风险时，可能存在一些计算误差，因此，今后将研究重点放到数据质量检测以及多源数据融合上，为其提供更可靠的技术支持。