基于BP神经网络的电网故障定位

张繁斌，范英乐，刘宝童，刘璐，李贝贝，李熙

(国网江苏省电力有限公司徐州供电分公司，江苏 徐州 221000)

电网发生复杂故障后，调控中心在短时间内将会收到系统采集的及监控人员汇报的各种信息，多类信息从各方面反映了故障情况。极端情况下故障发生伴随通道退出，将有大量信息无法上传或存在畸变，这就要求调控人员利用积累的经验快速确定故障元件，但这非常依赖调控人员的经验图谱，在发生复杂故障时，各类不正确的信息会对调控员的正确决策造成干扰，对电网安全运行造成一定隐患。国外曾发生过多次严重电网故障，因不能快速准确诊断，使得电网恢复时间很长，造成了很大的损失，例如2016年一次强台风天气袭击了南澳大利亚州，导致风电机组大规模脱网，最终导致了全州大停电事件[1]。2018年3月，巴西北电南送的特高压直流输电直流通道阻断，引起巴西电网大范围潮流转移，系统振荡，区域电网网间联络线的失步、距离和过电压等保护动作跳闸，巴西电网解列为北方、东北和南方3个独立运行电网[2]。2020年8月，由于罕见高温引起的负荷增长以及区域间电力协调能力不足，同时应对新能源波动的灵活调节能力不足，引起了美国加州大停电事件[3]。另外巴西发生的大停电事故，荷兰的变电站由于失压故障引发的大面积停电事件，以及日本由于地质灾害地震海啸引发的大停电事件等在全球造成了极其恶劣的影响[4-7]。这些大停电事件的发生都是由于某个故障发生不能及时判断处理而引起的连锁反应。若是能在故障发生后快速准确识别故障区域，那么调控人员便可在短时间内根据故障区域及影响范围制定合理事故处理方案，便可减轻因电网事故产生的恶劣影响，这也正是本文研究故障定位的重要意义。但是在短时间内正确甄别上传的正确信息是有一定难度的，正是基于这点，利用人工智能技术的非线性处理能力便可以很好解决这个问题。

1 故障定位方法及神经网络结构

1.1 故障定位方法

目前故障元件定位方法有很多人工智能方法，其中神经网络方法最为适用，有的已应用在调控运行中[8-12]。其中专家系统过多依赖于其在专业领域积累的经验，且维护烦琐；Petri网当在其处理复杂问题时会出现组合爆炸的情况，对电网拓扑变化不能及时反应，且容错能力较弱。神经网络等人工智能方法在电网应用喝多，文献[13]分析了电网发展新特点和调度控制面临的挑战，进而按照人工智能与现有技术体系深度融合的思路,开展电网调控领域人工智能应用技术框架研究，提出了总体思路及目标。文献[14]提供了一种基于长短期记忆(long short term memory,LSTM)网络的电网动态轨迹趋势预测方法。文献[15]利用粒子群算法和列文伯格-马夸尔特算法对神经网络进行优化改进，建立了基于粒子群算法优化的BP神经网络负荷预测模型。文献[16]运用机器学习算法构建了塔筒倾覆故障模型，可以反映设备状态，检测模型特征值的变化趋势，实现塔筒倾覆状态的在线检测和劣化过程的早期预警。

针对复杂电网的故障元件定位，神经网络因其具有强大的非线性处理能力，在应用中取得了很好的效果。本文利用BP神经网络对故障发生时的各类信息进行筛选，自动弱化畸变信息，强化有用信息，通过内部机理的非线性运算，通过神经网络输出层输出量化结果，便可以迅速定位故障元件。

电网的调控中心是电网运行指挥中枢，而调控人员的决策则是指挥中枢的核心。目前事故后的调度决策大部分仍以人工分析为主，主要依靠调控人员以往的处理经验，当遇到一些特殊情况，例如发生信息缺失或畸变，根据已有繁杂信息无法及时推断故障工况时，便会在一定程度上加大了调控人员的工作难度和工作压力，给准确快速恢复供电增加了难度。若在电网发生故障后，利用BP神经网络处理非线性问题的能力，通过对以往电网的历史运行数据进行学习，首先对各类上传的信息进行判断筛选，由此再获得相应的故障区域，以辅助调控人员的运行决策，为其准确快速处理故障恢复正常供电提供支撑，同时能缩短调控运行及检修人员的判断时间，提高处理效率，以致在短时间内消除故障，保证电网安全运行。

1.2 神经元模型

单个神经元模型是神经网络最基本的组成单元，也是用来处理非线性映射的最基本单元，其中ANN应用于电网技术是在20世纪80年代后期，便形成了BP神经网络诊断方法。BP神经网络由若干人工神经元连接而成，它是一种处理非线性问题、并可自动调整拟合的智能系统，在处理复杂问题时具有独特的优势[17-22]。

神经网络由单个神经元模型组成，由它来构成各种不同形式的神经网络，包含3个基本模型：连接权值、求和单元、激活函数。其基本结构如图1：

图1 单个神经元模型Fig.1 Single neuron model

连接权值即连接强度，其正负代表了激活和抑制状态，对应生物中的“突触”的连接强度，是非线性拟合的重要组成部分；输入信号是外界的输入量，是在求和单元进行线性计算；激活函数用来进行非线性计算，并且用于限制输出振幅，一般在(0,1)之间。可用下列公示表示:

(1)

yk=f(uk+bk)

(2)

上两式中，xi(i=1,……,m)代表输入信号；wik(i=1,……,m)是连接权值；uk则是经过求和单元之后的输出；bk为阈值；f(·)为激活函数；yk为输出信号。

1.3 BP神经网络结构

神经网络按照连接形式，最经典的网络结构就是前馈型和反馈型。BP神经网络属于前馈型，前馈型是指数据由上至下单向传递，只从输入层传递到输出层，没有反馈过程。图2则为多层前馈型的拓扑结构，其中xi(i=1,……,N)代表输入信号，yi(i=1,……,N)代表输出信号。信号的处理方向为，输入数据通过输入层进入神经网络，通过若干隐含层的非线性处理后，再通过输出层输出结果。

图2 前馈型网络结构模型Fig.2 Feedforward network structure model

2 BP神经网络传播原理

神经网络有多类算法，其中反向传播算法是一种易于理解且可行的迭代方法[23-28]，适用于电网故障定位中。BP(Back Propagation)神经网络是根据误差反向传播算法训练的。误差反向传播算法有两个过程：数据的正向传递与反向传递。其应用在电网故障定位时，首先设置一个神经网络的目标值，将各类上传的信息(例如保护装置及开关状态)通过一定规则转换为数字量，这些量值依次通过输入层、隐含层和输出层。隐含层的作用是在内部通过激活函数和连接权值对数据进行非线性计算，然后将结果在输出层输出；如果输出结果与预期目标有差距，且偏差达不到目标值，则将偏差进行反向传递，按照梯度下降算法继续迭代来更新新的权值，最终以使得误差满足所设定的目标值，此时通过迭代形成的权值就是固定问题所需要的值，将所需要诊断的信息通过一定规则转换为数字量后，通过已经固化权值的神经网络的非线性运算后，便可得到最终的计算数据，将其按照一定规则进行转换，便可以得到本文故障定位的结果。

2.1 训练函数

BP神经网络中常用的训练函数有log-sigmoid型函数logsig、tan-sigmoid型函数tansig以及纯线性函数purelin。同一训练函数在不同情境下的效果也不相同的，训练函数主要用来全局调整权值和阈值，用于达到整体误差最小。logsig及其tansig型函数的输出范围分别为(0,1)与(-1,1)。图3为logsig型函数:

图3 logsig函数模型Fig.3 Logsig function model

2.2 反向传播算法

误差反向传播，即从输出层反向逐层计算每层误差，不断更新权值、阈值，不断迭代直至满足目标的要求。

若训练样本包含P(1-P)个样本，误差的二次型准则函数为：

(3)

网络对P个训练样本的总体误差函数为：

(4)

2.3 反向传播算法流程

BP神经网络的动态运算流程的非线性映射能力强，具有以任意精度逼近目标值的计算能力。以“黑匣子”模式将输入变量与输出目标值联系起来，可运算较复杂的问题。但也存在着例如容易陷入局部极小值，隐含层节点数的选择没有严谨的数学依据等。针对以上问题的改进方法有附加动量法、自适应学习速率法等。BP算法流程主要包含参数初始化、输入训练样本、计算各层的输出值、计算各层的信号误差、调整权值和阈值等过程，直至满足总体训练误差的要求，如下：

图4 BP算法流程图Fig.4 Flow chart of BP algorithm

3 电网故障定位算法

3.1 电网拓扑结构

图5 配电网拓扑结构Fig.5 Distribution network topology

本系统划分成为了五个故障区域，分别为Sec1、Sec2、Sec3、Sec4、Sec5；断路器为QF1、QF2、QF3、QF4、QF5；并且均配有过电流保护CO1、CO2、CO3、CO4、CO5；Sec1和Sec3区域分别装有距离保护RR1和RR3，为过流保护的后备保护，其中RR1为Sec2～Sec5提供后备保护，RR3为Sec4和Sec5提供后备保护。

为了验证BP建模方法对电网故障定位的有效性，本小节以图5所示的电网结构为例说明分析。

3.2 故障决策表的构建

故障决策表是用来作为设神经网络输入和输出的，通过1或0来表示是否动作，并根据电网结构和保护情况来构建的表即为故障决策表。例如区域二(Sec2)发生故障，过流保护(CO2)便会动作，则在决策表中，QF2和CO2的值便是1，其余为0。故障决策向量可以写为[QF1-QF5；CO1(RR1)-CO5；区域]。其中保护及断路器状态信息作为输入向量，五个故障区域(Sec1～Sec5)用作神经网络的输出向量，若干个输入量对应一个输出量。本算例中设置一组向量，根据保护及开关情况，一组向量中共13组状态量，其中有12个为判断条件，1组为决策结果，12个判断条件对应一个结果，判断条件即为训练神经网络的输入量，结果即为输出量。以故障区域2为例，其向量为[0 1 0 0 0 0 0 1 0 0 0 0；S2 ]。根据故障区域的不同(五个故障区域，一个无故障区域)，构建13组用于BP神经网络训练的向量，即训练样本，用此样本来训练BP神经网络，最终得到符合要求的网络结构。

3.3 故障信息的获取

故障信息即为故障样本，用以检验训练好的神经网络是否具备诊断功能。与故障决策表不同的是此中信息不尽是正确数据，此外还含有错误动作信息。在故障信息向量中，表示方法为括号外为真实数据，括号内数据表示为没有信息畸变时的正确信息。例如仍以故障区域2为例，构造一故障信息向量[0 1 0 0 0 0 0 1 1(0)0 0 0；S2]，代表“CO3”数据发生了畸变，本身CO3没有动作，但是上传信息过程中发生了畸变，误传为动作。

3.4 BP神经网络建模

BP神经网络建模包含输入层、输出层、隐含层以及训练函数等主要因素的确定，其中以隐含层的确定最为重要。

输入层的确定：输入层节点的确定和样本有关，需要根据特定样本来选择，其中样本提取出的故障决策表决策元素的数量便是BP神经网络输入层节点的数量，本案例中判断条件有12个，故输入层节点数为12。

输出层的确定:输出层节点的确定和诊断区域有关，其数量代表着待诊断的元件或者区域的数量，即元件或区域的数量与输出节点的数量相等。本案例中输出有6个(5个故障区域以及1个无故障区域)，故输出层节点数为6。

隐含层节点数的确定:隐含层的节点数目前的应用一般根据经验公式得到。

根据经验公示：

(5)

上式中，m为输入层节点数，n为输出层的节点数，而结果l则为隐含层的节点数，d为0-10之间的整数，易知m为12，n为6，则根据上式可以得到隐含层节点数在4-14之间。通过经验公式只能得到一个大致的范围，并不能确定某一具体的层数。所以为了选取最合适的隐含层，本文提出一种选取最佳隐含层节点数的方法：设定目标误差0.001，学习速率0.01，记录达到目标误差产生的训练误差，选择最小的即为最合适的节点数。

表1 隐含层节点数与训练误差、迭代次数Tab.1 Number of hidden layer nodes, training error and iteration times

下图为根据表1绘制的误差关系图：

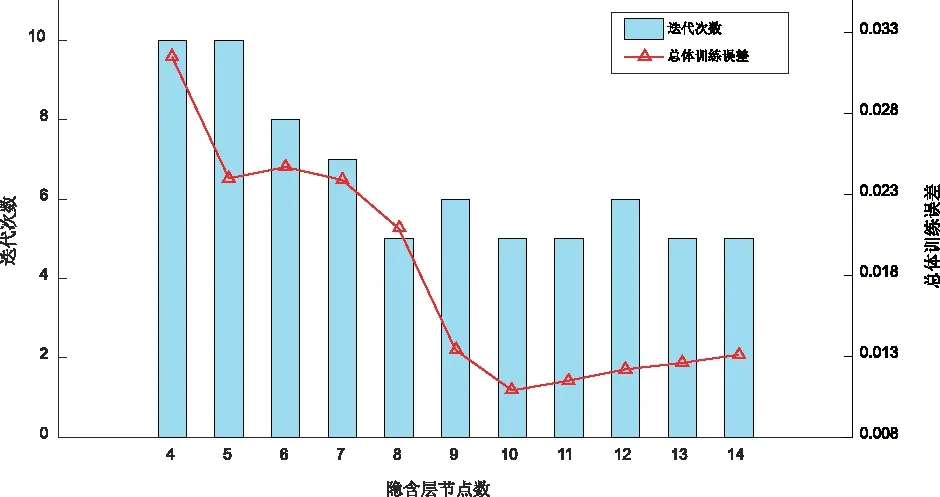
图6 隐含层节点数与总体训练误差、迭代次数关系Fig.6 Relationship between the number of hidden layer nodes and the overall training error and the number of iterations

根据图6可以，迭代次数最小的隐含层节点数有8、10、11、13、14，而根据误差训练曲线图可知，当隐含层节点数为10或11时，误差较小，综合迭代次数及训练误差，本文选择隐含层节点数为10。训练算法则选用trainlm算法。

4 实例分析

根据图5电网拓扑结构，首先通过构建好的故障决策表(13组向量)，根据已经确定的BP神经网络参数对其进行训练，在达到所设定的目标值时便停止迭代，得到一个训练结束参数固化的BP神经网络，用此神经网络结构再对不含于初始训练样本的数据进行计算，来达到故障定位的目的。训练过程中的误差曲线如下：

图7 训练误差曲线Fig.7 Training error curve

为了能够客观评价此神经网络对电网故障定位的作用及效果，用此网络对含有畸变量的故障信息表进行诊断，进而得出诊断结果进行判断，诊断结果如下：

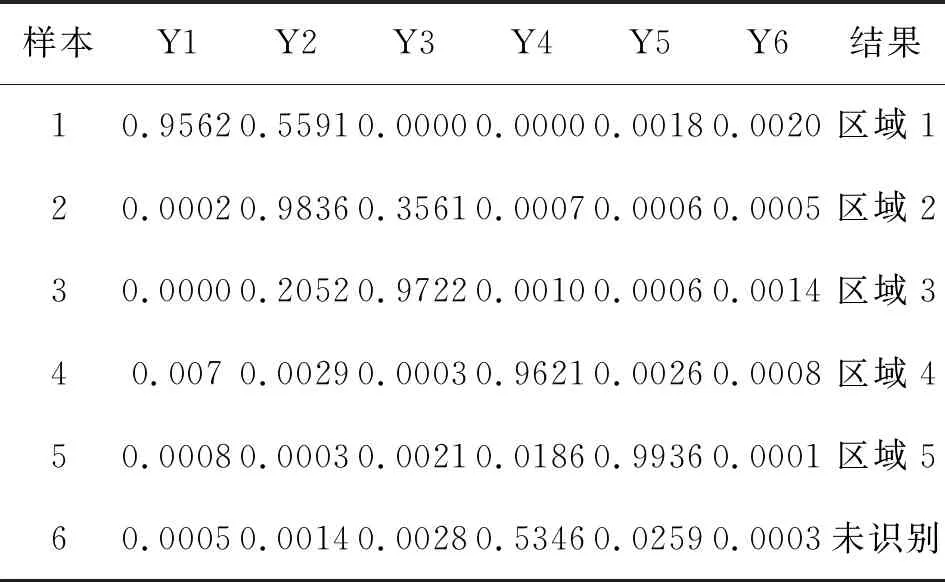
表2 诊断结果Tab.2 Diagnostic results

如表2中的数值，用(0，1)范围内的数值来代表诊断结果，数值越大越接近于1，说明诊断为本区域；数值越小越接近于0，说明故障区域为本区域的可能越小。从诊断结果可以看出，对于样本1-5可以正确诊断出故障区域，对于样本6(复杂故障)未能准确识别。说明BP神经网络用于电网故障元件的定位是有效的，在发生信息畸变的时候，利用其容错性强的能力可以正确识别故障区域，达到了预期目标。应用在电网调控运行时，可以在发生故障第一时间从各类上传的警告及动作信息中判断出故障区域，帮助调控运行人员准确判断，从而辅助决策，正确处理电网故障，有利于电网安全运行。

5 结论与展望

本文提出了一种基于人工智能技术进行电网故障诊断的新思路，详细给出了利用BP神经网络进行电网故障定位的算法流程，以及各项参数的确定方法，包含输入层、输出层以及隐含层节点数的确定方法，给出了具体计算步骤和分析过程，最后通过算例分析说明了其有效性和准确性。结果表明：

(1)BP神经网络非线性拟合能力强，利用BP神经网络其容错性强的特点，模拟人脑非线性拟合的功能，可以看出对于复杂的问题的判断具有很好效果，将其应用在电网故障定位中是可行且有效的，有助于电网安全运行。

(2)利用BP神经网络进行电网故障区域定位，可以很好甄别畸变信息，当电网发生单一故障时，能够自动过滤掉畸变无用信息，准确地定位故障区域，得出诊断结果，有助于调控运行人员准确快速处理电网故障，保障电网安全运行。

(3)在面对非常复杂的故障，或所诊断的状态信息畸变率比较高时，诊断结果存在一定的局限性，因此未来对于这种局限性可以融合它类人工智能技术进行改进。