多阶段垄断竞争的动态博弈分析
朱 捷,王生喜
(1.广东科技学院,东莞523083; 2.厦门大学嘉庚学院,漳州 363100)
垄断竞争是产业组织理论研究的重要内容.Stackelberg于1934年建立的双头垄断动态模型成为这一研究领域博弈分析的标准版本.Selten[1]于1965年引入了子博弈完美均衡的概念.文献[2-6]深入研究和发展了Stackelberg模型.文献[7-8] 将逆向归纳的思想延伸到一般的扩展式博弈.在非合作博弈的经典文献中,对双头垄断动态博弈模型都有详尽讨论[9-15].
从博弈论的角度出发,Stackelberg模型是一个完全信息的二阶段双人博弈问题.在现实经济活动中,下述现象并不鲜见:若干个领导企业首先选择行动(决定产量或价格),一定数量的跟随者随后采取行动,跟随者的后面还有跟随者,如此等等.系统研究这类多阶段、多人参与的垄断竞争模型将会为产业组织的理论研究提供更加丰富的分析工具.本文在上述现实背景下建立了一个多阶段,多企业参与的不完美信息动态模型,在一般条件下讨论了子博弈精练解的存在性,并在线性需求函数的条件下给出该博弈的解析解.
1 基本模型

支付函数ui=ui(Q)=ui(q1,…,qk1,qk1+1,…,qk2,…,qkm-1+1,…,qn)T足条件:
1)对每个qj∈R+,ui单调递减;


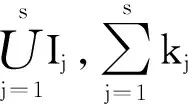
本文构造的上述模型简称为MMS模型.
2 子博弈精练解的存在性


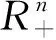
定理2 MMS模型的子博弈精练解存在且唯一.
证明:设juj表示支付函数uj(Q)=uj(Qkj,Q-kj)关于Qkj的梯度向量,即

第一步:对第n组(即最后一组)共km个企业Im={km-1+1,km-1+2,…,km}来说,支付函数为uj=uj(Qkm,Q-km)(j=km-1+1,km-1+2,……,km).

(1)

qj=hj(q1,q2,……,qkm-1)(j=km-1+1,j=km-1+2,……,km)
(2)
式(2)恰好是Im内的局中人对其余局中人选择的反映函数.其向量形式记为:
Qkm=hm(Q-km)
(3)
易知hm为连续且可微的km维向量函数.

uj=(Q-km,hm(Q-km))(j=km-2+1,km-2+2,……,km-1)
再记Q-km=(Qkm-1,Q-km-1),注意本段中的(Qkm-1,Q-km-1)是对向量Q-km的划分,向量Qkm-1的补Q-km-1是(n-km-km-1)维向量.Im-1内诸企业的选择满足极大化问题
一阶条件
(4)
与第一步的讨论类似,方程组(4)有如下形式的向量解:
Qkm-1=hm-1(Q-km-1)
(5)

uj=uj(Qkm-1,Q-km-1,hm(Qkm-1,Q-km-1))=
uj(Qkm-1,hm-1(Q-km-1),hm(Q-km-1,hm-1Q-km-1))=
Uj(Q-km-1)=Uj(Qkm-2Q-km-2)
(j=km-3+1,km-3+2,……,km-2)
(6)

uj=Uj(Qkm-t+1,Q-km-t+1)(j=km-t+1,km-t+2,……,km-t+1)

Qkm-t+1=hm-t+1(Q-km-t+1)
(7)


uj=Uj(Qkm-j,Q-km-j,hm-j(Qkm-j,Q-km-j))
(j=km-j-1+1,km-j-1+2,……,km-j)
第m步 :对第(m-m+1)组 (第1组)的k1个企业I1={1,2,…,k1},其支付函数具有如下k1维形式
uj=Uj(Q-k2)=Uj(Qk1)j=(1,2,……,k1)


(8)

(9)
将式(9)逐步回代到式(7),(5),(3)中得
…… …… …… ……
由上述m步的推导,博弈MMS的子博弈逆向递归解为
(10)
3 基于利润目标的子博弈精练解
3.1 线性需求函数下解的形式
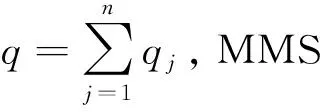
(11)

仿照定理2的证明过程,对最后一组km个企业,其一阶条件为:
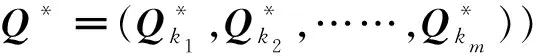
(12)
式(12)的规范形式如下:
(13)
式(13)的m阶系数矩阵为
右端向量记为bm(Qkm-1)
显然行列式|Am|=km+1,故Am非奇异,以下称Am为LMMS第m阶段的反应矩阵.式(13)的矩阵形式记为AmQkm=bm(Qkm-1),从而Im中企业的反应向量函数为
其中
j=1,2,…,km-km-1+1≤ks≤km
(14)
式(14)即为Im中企业对其他企业所做选择的最优反映.这组反映函数表明,Im中企业的选择除受到本组企业的影响外,还受到Im之外的所有企业的产量选择、边际成本以及本组成员数量km的多重影响.
将式(14)代入Im-1内企业的支付函数,整理得到
(i=km-2+1,km-2+2,…,km-1)
(15)
不难得到式(15)对应的反映矩阵Am-1.由定理2(解的唯一性)知Am-1非奇异.以此类推,其余各阶段的反应矩阵Am-2,Am-3,……,A2,A1均非奇异.由此我们不难总结出下述结果.
定理3 在LMMS模型中设各阶段的反应矩阵为Am,Am-1,……,A2,A1,各阶段反应函数组(规范形式)的右端向量为bm,bm-1,……,b2,b1,其中bt为Qkt-1的函数.该博弈的子博弈精练解为:
3.2 二阶段博弈的显式解
由对称性知
(16)
将式(16)代入第一组企业的支付函数,其一阶条件
记
(17)
式(17)即为第一组企业的最优产量选择,第二组企业的最优产量选择为

当k=1时,LMMS即为Stackelberg模型.
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

