北京地铁双超列车运行图编制方法
宿帅,刘旭,王学楷,唐涛,曹源
(1.北京交通大学,a.轨道交通控制与安全国家重点实验室,b.电子信息工程学院,北京100044;2.北京地铁运营有限公司,北京100044)
0 引言
重大疫情给乘客密集的地铁运营带来了重大挑战,为使疫情下地铁系统乘客密度满足公共卫生服务要求,北京地铁决定大幅提升所有线路运力,旨在降低既有巨大客流出行时列车车厢内的满载率,减少公共运输体系中疫情传播的可能性。为此,北京地铁在大多数线路运用“超常”条件下的“超强”运行图(“双超”运行图),并实施增加车次,多交路运行,减少列车运行间隔,大站快车等措施。利用有限的车辆资源,在既有的线路条件下,实现对客流时空规律的精准分析,线路资源的精准运用,运力的精准投放,以及列车满载率的实时精准监测,降低列车满载率。
(1)精确挖掘线网客流的时空分布规律。分析各条线路客流在空间、时间等多个维度的分布特征,分析乘客在换乘站的换乘方向和换乘时间,作为精准配置运力的基础。
(2)精准运用和配置网络资源。运用有限的网络配线资源和车辆基地,依据客流分布规律,通过多交路行车,双向不平衡行车,大站快车,越行快车,以及减少停站时间等措施,提高线网资源配置的精确性和效率。
(3)精准匹配运力、运量。按照运力与运量精准匹配原则,根据网络客流时空分布规律,因地制宜,采取不同的措施组合,编制网络化列车运行图,使图定运力与实际运量相匹配。
(4)精准监测运行列车实时满载率。搭建专用平台,实时监测和分析各线路中各车站的出入站乘客数、换乘乘客数及列车满载率信息;通过相应的应急机制,在适当时刻调整行车,使提供运力与实时客流精确匹配。
在面向乘客服务的列车运行图优化编制研究中,CANCA 等[1]以最小化乘客等待时间为优化目标,提出一种考虑动态乘客需求的MINLP(Mixed Integer Non-linear Programing)模型并运用GAMS(General Algebraic Modeling System)软件求解问题。ZHU等[2]以列车运营追踪间隔为决策变量,降低乘客等待时间和旅行时间为优化目标,提出运行图优化的双层规划模型,并采用GA(Genetic Algorithm)方法作为问题优化算法。NIU 等[3]以最小化乘客等待时间为目标,提出一种适用于列车跳停场景的运行图优化方法,建立MINLP 模型并用GAMS 软件对问题进行求解。以上研究均针对单交路模式下的运行图优化编制问题,在多交路模式研究中,李正洋等[4]以不同交路列车的编组数及发车频次为决策变量建立MINLP 模型,通过优化降低了乘客等待时间和运营成本。SANDER 等[5]基于列车多交路运行场景,通过运行图优化降低了乘客等待时间和取消的计划车次数。JI等[6]建立马尔可夫模型并设计启发式方法求解问题,模型中优化目标是最小化乘客等待时间、乘客旅行时间和运营成本。许得杰等[7]提出的优化模型以增加满载率均衡性和乘客等待时间、列车总运行时间和走行公里为优化目标,并采用受控随机搜索求解问题。
“双超”运行图的重要目的是降低列车满载率,使其满足防控要求。但以往针对多交路运行图的优化编制研究尚未考虑这一特殊条件下的优化指标。因此,本文依据“双超”运行图的编制流程,提出面向车厢低满载率的“双超”运行图优化编制方法,建立开行方案和列车运行图双层规划优化模型,并用CPLEX软件求解问题。相比以往方法,该优化模型的创新点在于可在车辆资源有限的前提下,根据客流信息优化列车运行图,使车厢满载率最低。
1 “双超”运行图双层规划模型
本节基于图1所示的“双超”运行图编制流程,建立面向车厢低满载率的双层规划模型,对列车开行方案及列车运行图进行优化。
在双层规划模型中,上层模型以降低平均满载率为目标,在基于时空分布规律确定的交路方案基础上得到列车开行方案中运行各交路的列车数;下层模型在上层模型优化结果的基础上,优化得到满足列车运行约束的运行图参数;上层模型再基于下层模型优化结果对列车开行方案参数进行优化。通过迭代优化得到面向车厢低满载率的列车运行图。
1.1 上层模型
在上层模型中,根据客流时空分布规律确定交路方案。设β={1,2,…,S} 为地铁线路中的车站集合,上行、下行站台共2S个。可作为折返站的车站集合θ⊂β,共有T个。则线路中共有条可选交路,需从中选取若干条作为实际列车运行交路。确定交路方案的过程中,先分析客流的时空特征,利用客流在时间维度上的不均衡特性,将全日行车时间分成平峰、高峰时段;利用空间不均衡特性确定交路方案。具体地,根据客流信息计算客流时间不均衡系数,并将时间不均衡系数大于1.5 的时段设为高峰时段,再计算高峰时段的客流空间不均衡系数。若各区间的空间不均衡系数均小于1.5,则采用单交路运行;否则,开行大、小交路,小交路包含全部空间不均衡系数大于1.5的区间,并尽量包含该系数大于1的区间。

图1 “双超”运行图的基本编制流程Fig.1 Basic process for designing train timetable in epidemics
基于交路方案,对列车开行方案进行优化。不失一般性,以下述交路方案为例介绍模型:运行交路集合为ε={1,2} ,其中,r=1 为大交路,包含车站集合β1=β,区间集合φ1;r=2 为小交路,包含车站集合S2={1,2,…,s(turn)},其中,折返站s(turn)∈θ,区间集合φ2。
第n次迭代的决策变量是运行大、小交路的列车数I1(n)和I2(n),需要满足可用车底总量约束条件,即

式中:I为可用列车数。
设第n-1 次迭代得到各交路的全周转运行时间为Fr(n-1),∀r∈ε。则运行大、小交路列车的平均发车间隔时间为

因此,小交路和小交路外区域内行车提供的运力Y1、Y2分别为

式中:Yv、nv分别为车厢定员和列车编组数。根据客流和运力计算上行各区间的列车满载率为

式中:j为线路中区间的索引;为区间j内上行方向的断面客流量。
同理可得下行各区间的列车满载率。式(4)为非线性函数,为便于后续求解,采用分段仿射方法将该函数近似转换为线性函数[9]。
为满足疫情防控要求,尽量使各区间的列车满载率低于50%,因此,上层模型的优化目标为

式中:为全线各区间上、下行方向列车满载率超出满载率指标的平均值;J为线路区间总数。
1.2 下层模型
在第n次迭代时,下层模型在上层模型得到的各交路开行列车数I1(n)和I2(n)的基础上,对列车运行图参数进行优化求解。
首先,为保障列车运行安全,运行交路为r∈ε的列车在各站的发车间隔需满足
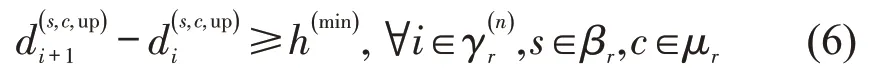
式中:γr(n)为第n次迭代时交路r中运行列车的集合;为上行方向运行列车i在第c个运行周期内,从车站s发车的时间;h(min)为最小发车间隔。
其次,在小交路各车站中,会存在运行不同交路的列车相邻的情况,因此还需要满足安全约束条件为


在列车运行中,运行交路为r∈ε的列车在各区间的运行时间需满足

式中:T(s,s+1,up,min)、T(s,s+1,up,max)分别为最小区间运行时间和最大区间运行时间;为列车i在上行方向运行到第c个周期内,到达车站s+1的时间。
在“双超”运行图中,列车停站时间可以根据客流数据计算获得,本文采用经验公式[8]计算上行方向列车在车站s的停站时间D(s,up),即

此外,列车折返时间需要满足约束条件为

式中:B(1,min)、B(S,min)分别为列车在大交路折返站1和S处的最短折返时间;B(sturn,min)为列车在小交路折返站s(turn)处的最短折返时间。
在折返站s∈θ处,列车最短折返时间B(s,min)的计算公式为

式中:Ba(s)、Bd(s)、Bb(s)分别为清人时间、转台时间和上人时间;Bi(s,front)、Bo(s,front)、Bi(s,back)、Bo(s,back)分别为列车在站前、站后折返时的入库及出库时间;二元变量δ(s)判断列车在折返站s采用的折返方式,若采用站前折返方式,δ(s)=1 ,否则,为站后折返,δ(s)=0。
运行交路r∈ε的列车全周转运行时间为

全周转运行时间需要满足约束条件为

式中:Fr(min)为交路r的最短全周转时间。
综上所述,面向车厢低满载率的双层规划线性模型为
优化目标:式(5)
约束条件:式(1)~式(4),式(6)~式(14)
本文基于双层规划线性模型,运用CPLEX 软件对问题进行求解。
2 仿真结果分析
基于亦庄线实际数据,通过仿真对提出的“双超”运行图优化编制方法的有效性进行验证。
亦庄线某日上行、下行方向的分时断面客流量如图2所示,其中,亦庄火车站-宋家庄方向为上行方向,按该方向将车站依次编号为1~14,将区间依次编号为1~13。
根据客流数据计算得到客流时间不均衡系数,如图3(a)所示,早高峰时段为7:00-10:00,晚高峰时段为18:00-19:00。其中,全日最大断面客流出现在8:00-9:00,该时段内客流空间不均衡系数如图3(b)所示。
该时段有3 个区间在至少一个方向上的空间不均衡系数大于1.5,因此,需开行大小交路,且小交路应包含这些区间。同时有2 个空间不均衡系数大于1 的区间。结合实际运营,亦庄火车站、同济南路、旧宫、宋家庄(序号分别为:1,5,11,14)这4个车站具备折返条件,得出小交路折返站分别为同济南路和宋家庄。
基于双层规划模型求解早、晚高峰列车开行方案和列车运行图,图4为优化后的早高峰运行图。

图2 北京地铁亦庄线全日分时断面客流量Fig.2 Passenger flow for each hour in Beijing Metro YIZHUANG line
表1为优化后开行方案和运行图参数与当前未优化列车运行图的对比结果。

图3 客流不均衡系数Fig.3 Unbalanced factor of passenger flow

图4 早高峰时段运行图Fig.4 Train timetable in morning peak
表1结果表明,在运行图优化后全部22列列车上线运行,新增3列运行列车,运行大交路、小交路的列车分别为13 列和9 列。优化后在小交路中行车提供的运力比未优化时提升33.3%(设全列定员为1440人),进而使优化后上行、下行列车的最大满载率分别降低21.1%和16.6%,更接近列车满载率低于50%的防疫要求。
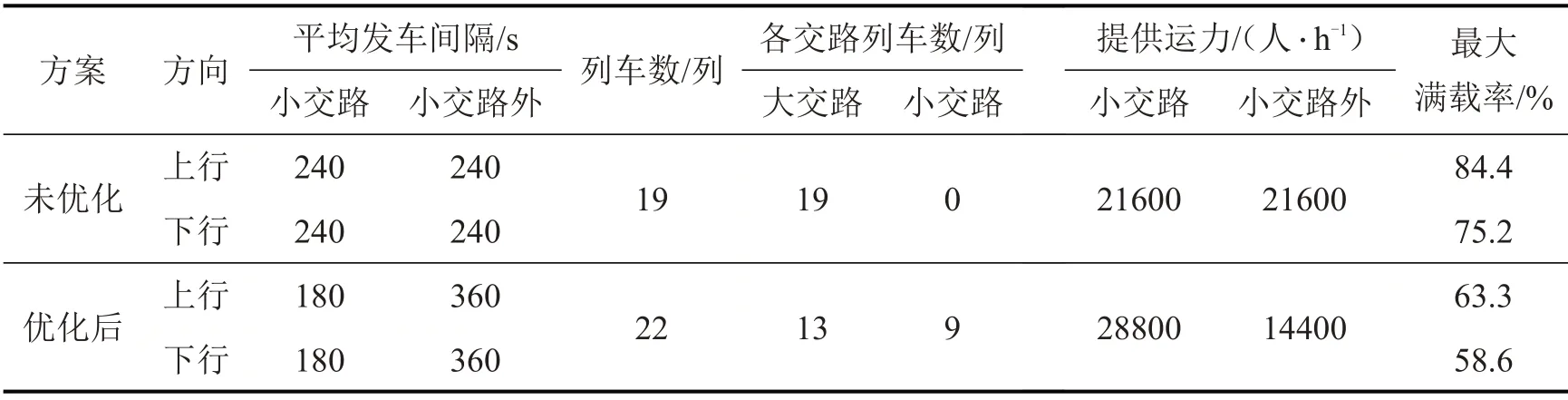
表1 优化前后早高峰开行方案和运行图参数Table 1 Parameters of operation plan and timetable in morning peak
优化后列车最大满载率下降的原因主要有两个方面:首先,运行列车数的增加使全线列车可提供的运力增加,整体上降低了列车满载率;其次,在列车数一定的前提下,通过开行大交路、小交路对运力进行优化配置,在客流较大的小交路中提供更多运力,为其他客流较少的区间提供相对较低的运力。该方法使运力得到更高效的利用,通过迭代优化开行方案和运行图使各断面的满载率更均衡,降低最大满载率,使“双超”运行图防疫效果更佳。8:00-9:00 时段优化前后各断面满载率如图5所示。
图6为优化后晚高峰运行图,表2为优化前、后的开行方案和运行图参数。表2结果表明:晚高峰运行图优化后,运行大交路、小交路的列车分别为13列和9列,在小交路中行车提供的运力比未优化时提升66.7%;优化后上行、下行列车的最大满载率分别降低21.1%和16.6%,满足列车满载率低于50%的防疫要求。列车最大满载率下降原因同样是运行列车数的增加使整体运力增大,以及优化配置运力使各断面满载率更均衡。图7为优化前、后的各断面列车满载率。

图5 优化前后8:00-9:00时段各断面列车满载率Fig.5 Load factor for each segment in 8:00-9:00 before and after optimization

图6 晚高峰运行图Fig.6 Train timetable in evening peak

表2 优化前、后晚高峰开行方案和运行图参数Table 2 Parameters of operation plan and train timetable in evening peak

图7 优化前、后18:00-19:00各断面列车满载率Fig.7 Load factor for each segment in 18:00-19:00 before and after optimization
3 结论
为降低病毒在乘客间传播的可能性,本文基于疫情下“双超”列车运行图的优化编制流程,提出一种面向车厢低满载率双层规划模型,用于优化列车开行方案及列车运行图。该方法可在车辆资源有限的前提下,根据客流信息优化获得使车厢满载率最低的“双超”运行图。优化后,早、晚高峰中小交路列车运行所提供的运力分别增加了33.3%和66.7%,全线最大列车满载率分别降低了21.1%和23.2%。因此,所提方法可有效降低列车满载率,进而减少疫情在公共运输体系中传播的风险,为疫情下城轨运输体系提供了良好地支撑。

