基于空铁联运OD可达性的高铁时刻表优化模型

可钰，聂磊*，袁午阳,2

(1.北京交通大学，交通运输学院，北京100044；2.中国铁道科学研究院集团有限公司，运输及经济研究所，北京100081)

0 引言

高速铁路和航空的快速发展为航空-铁路联合运输提供发展契机。空铁联运作为比高铁更快、比飞机更经济的运输方式，可以满足日益增长的中、长途旅客出行需求。其优势之一在于可以覆盖更多的客流起讫点(Origin-Destination，OD)，为机场辐射的周边地区提供更多的出行选择机会，使旅客可以往返更多的目的地。如果高铁时刻表不能与航空时刻表有效衔接，尤其当空铁联运换乘枢纽的高铁服务频率较少时，将直接影响空铁联运的OD可达对数，可供旅客出行的选择受限，进而降低服务水平。因此，通过优化高铁时刻表提升空铁联运OD可达性的研究具备现实意义。

国内外学者研究空铁联运的内容主要有：LI等[1]以京广运输通道为背景，基于Logit模型分析空铁联运旅客的选择行为，预测市场分担率，并进行敏感度分析，发现旅行时间是影响空铁联运分担率的最重要因素；SOCORRO 等[2]针对机场具备能力约束和无能力约束两种情况，通过理论模型分析空铁联运的社会和环境影响，为决策者提供评估空铁联运在不同假设场景中潜在影响的依据；CLEWLOW等[3]针对美国机场拥堵情况，研究铁路如何作为短途支线服务为长途航空服务提供支持，并从4个角度研究航空和高铁的连通性；KE等[4]以提高空铁联运服务的同质性为目标，对高铁列车运行图进行优化调整。

列车时刻表衔接优化问题也是当前的研究热点。郭根材等[5]建立面向周期列车运行图的接续约束生成模型，说明列车之间在接续时存在耦合关系，并提出消解冲突的破圈法。陈垚等[6]通过压缩末班车区间运行时间与非换乘站停站时间、延长换乘站停站时间，建立网络末班车时刻表优化模型。温芳等[7]通过优化各线路末班车的发车时刻，构建以各间隔起始时刻的关键OD 可达对数之和最大为目标的优化模型。胡倩芸等[8]分析铁路出站乘客转乘地铁的行为特征与客流规律，以衔接车站乘客总候车时间最小为目标，建立城市轨道交通发车时刻优化模型。

为充分发挥空铁联运的优势，本文面向空铁联运关键OD，基于固定的航空时刻表及既有高铁时刻表的开行方案，提出空铁联运OD 可达性约束，量化列车在空铁换乘枢纽的到发时刻、接续变量与可达性变量之间的关系，建立可达OD 数量最大、时刻表调整最小的双目标优化模型，并以石家庄正定机场为背景进行案例分析。

1 问题描述

近年来，可达性的概念被广泛应用于交通规划、土地利用等领域.由于研究对象和研究方法不同，既有研究对可达性给出不同的定义。可以表示利用特定的交通系统从一个地点到达任何土地使用活动的便利性[9]，或是在指定时间范围内从一个起点到达研究城市的数量[10]，也可以描述线网内可达的OD数量[7]。本文从高铁列车时刻表编制层面，以铁路和航空线网中的可达OD数量描述可达性。

空铁联运的OD 可达性关键取决于高铁列车和航班的接续关系。由于涉及到高铁和航空两段行程，旅客必须通过换乘才能完成一次完整的空铁联运出行。高铁和航班的接续时间既要大于旅客完成换乘的最短时间，又不能太长以免降低出行服务水平。满足以上时间要求，列车和航班才存在接续关系，完成空铁联运服务。如果旅客通过某高铁列车从出发车站到达空铁换乘枢纽，完成换乘过程，再通过接续航班到达目的机场，则称出发车站所在地和目的机场所在地组成的OD是“可达”的；类似地，旅客通过某航班从出发机场到达空铁换乘枢纽，完成换乘后，再通过接续高铁列车到达目的车站，则称出发机场所在地和目的车站所在地组成的OD是“可达”的。

针对高铁换乘至航空的空铁联运服务，考虑一条单线铁路的空铁联运OD可达性问题，车站和机场分布如图1所示。高铁线路包括车站A、B、C，其中，车站C位于空铁换乘枢纽；有3个机场，为机场C、M、N，机场C 位于空铁换乘枢纽。在该线路中运行2列列车，列车1始发于车站A，终到于车站C；列车2 始发于车站A，经停车站B，终到于车站C；有3 个离港航班，均始发于机场C，其中，航班1 和航班3 的目的地为机场M，航班2 的目的地为机场N。旅客在空铁换乘枢纽内可以接受的换乘时间范围为1.5～4.0 h。图1(a)为高铁时刻表优化前的空铁联运可达OD分布，列车1在8:00到达车站C，可以与航班1 接续，其接续时间为3.5 h，该列车与航班为OD 对AM 提供空铁联运服务；列车2 在12:00到达车站C，与航班3 接续，其接续时间为1.5 h，可以为OD对AM和BM提供空铁联运服务。基于当前高铁时刻表的空铁联运可达OD 数量为2 个，分别为AM和BM。优化后的高铁时刻表如图1(b)所示，列车2 于11:30 达到车站C，额外增加列车2 和航班2 的接续，可达OD 数量为4 个，分别为AM，AN，BM和BN，较优化前增加2个可达OD。

2 模型构建

2.1 问题假设

为简化模型，建立以下假设：

(1)高铁列车的开行方案已知。

图1 空铁联运可达ODFig.1 Illustration of OD accessibility AH intermodality

(2)航空的时刻表已知。

(3)仅考虑一次换乘。

(4)从接续的角度将空铁联运分为两类服务，分别为“高铁接续航空”(H-A接续服务)，“航空接续高铁”(A-H接续服务)。

(5)两类接续时间的时间窗已知。

(6)一列高铁可以服务多个车站，并通过空铁换乘枢纽与多架航班实现接续，可达性接续关系中的数量关系为多车站对应多机场。

2.2 参数定义

(1)模型中的参数

①列车和车站

I为列车集合，其中，I(T)为在空铁换乘枢纽停站的列车集合，I(N)为在空铁换乘枢纽不停站的列车集合，I(T)⋃I(N)=I；i,j分别为列车标识；为在空铁换乘枢纽停站，且在s站停站的列车集合。S为车站集合，s为车站标识，h为空铁换乘枢纽车站，Si为列车i经过的车站集合，为列车i的始发站，为列车i的终到站，为列车i和j共同经过的第一个车站，为列车i和j共同经过的最后一个车站，S(H-A)为H-A 接续服务中的车站集合，S(A-H)为A-H接续服务中的车站集合。

②航班和机场

F(L)为离港航班集合，p为离港航班标识，为航班p的离港时间，W为离港航班的终到机场集合，w为离港航班的终到机场标识，为终到机场是w的航班集合；F(O)为进港航班集合，q为进港航班标识，为航班q的进港时间，U为进港航班始发机场的集合，u为进港航班始发机场标识，为始发机场是u的航班集合。

③其他参数

ei,s表示列车i在车站s是否停车，取值为1 表示停车，取值为0 表示不停车；ri,s为列车i在区间[s,s+1] 的最小运行时间；αi,s和βi,s分别为列车i在区间[s,s+1] 的起、停附加时分；γi,s为列车i在区间[s,s+1] 的冗余运行时分；为列车i在车站s最小停站时间，为列车i在车站s最大停站时间；ψs为s站的列车最小到达追踪时间间隔，ζs为s站的列车最小出发追踪时间间隔；t(H-A-low)和t(H-A-up)分别为高铁接续航空的最小换乘时间和最大换乘时间，t(A-H-low)和t(A-H-up)分别为航空接续高铁的最小换乘时间和最大换乘时间；为原始时刻表中列车i在车站s的出发时刻，为原始时刻表中列车i在车站s的到达时刻；v为列车在始发、终到站偏移原始时刻表的时间窗。

(2)决策变量

为列车i在车站s的出发时间；为列车i在车站s的到达时间；φi,j,s为0-1 变量，当列车i在车站s早于列车j出发时其数值为1，否则为0；对于H-A 接续服务，为0-1 变量，当列车i与离港航班p接续成功时其数值为1，否则为0，为0-1 变量，当车站s所在地与机场w所在地组成的OD 可达时其数值为1，否则为0；对于A-H 接续服务为0-1变量，当进港航班q与列车i接续成功时其数值为1，否则为0，为0-1 变量，当机场u所在地与车站s所在地组成的OD可达时其数值为1，否则为0。

2.3 目标函数

模型第1个目标为最大化可达OD的数量。空铁联运包括两类接续服务，故目标函数Z1涉及到两类OD可达性变量，即

在优化空铁联运OD 可达性时，为保持运行图的稳定性，减少对既有时刻表的调整，以最小化时刻表调整作为第2 个目标Z2。以优化前和优化后列车在经停站的出发时间之差的绝对值之和作为调整量，即

2.4 约束条件

2.4.1 列车运行约束

每列列车i在各个区间[s,s+1]的运行时间需要考虑运行过程中的最小运行时间ri,s、起车附加时分αi,s、停车附加时分βi,s+1和冗余时间γi,s，即

每列列车i在中间站s的停站时间需要在规定的最小值和最大值之间，如果列车在车站无停车要求，相应的停站方案ei,s取0，即可保证列车的停站时间为0。停站约束为

在既有的原始时刻表中，列车的始发时间和终到时间已知。给定调整时间窗v，每列列车i在始发站的出发时间需要在规定的时间窗之内，同时在终到站的到达时间需要在规定的时间窗之内，其始发、终到时间约束为

2.4.2 列车安全约束

所有列车需要满足区间安全约束，既要满足列车出发追踪间隔约束和到达追踪间隔约束，同时在运行区间不能发生越行，故安全约束为

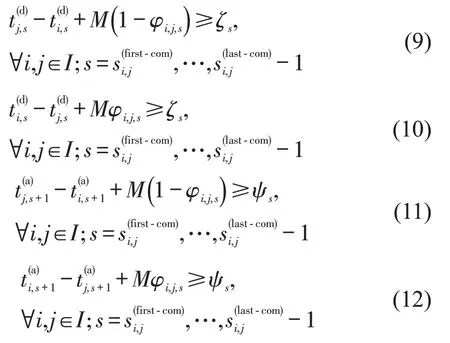
式中：M为一个数值很大的系数。

2.4.3 逻辑约束

所有列车在每个运行区间的逻辑关系约束为

2.4.4 空铁联运OD可达性约束

分别从两类空铁联运接续服务建立OD 可达性约束。

(1)H-A接续服务

当列车i∈I(T)在空铁换乘枢纽能够与离港航班p∈F(L)接续，即接续变量1，则说明两者的接续时间(离港航班p的出发时间与列车i在换乘站h的到达时间之差)大于等于最小的换乘时间t(H-A-low)，且小于等于旅客可容忍的最大换乘时间t(H-A-up)；否则，0。因此，存在约束为

车站s所在地与机场w所在地组成的OD若可达需要满足3 个条件：①由在空铁换乘枢纽停站，且在s∈S(H-A)停站的列车i∈Is(T)服务；②由终到机场是w的航班p∈Fw(L)服务；③列车i∈Is(T)与航班p∈Fw(L)的接续时间满足式(14)。所以，同时满足上述3 个条件的列车i和航班可以保证取值为1。OD 可达性变量与接续变量之间的关系为

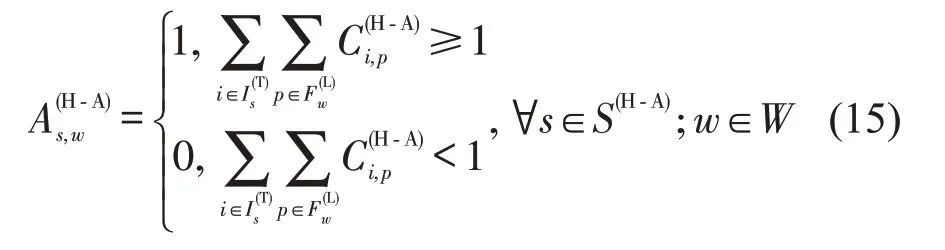
因目标函数为最大化可达OD 数量，式(15)等价于

对式(14)进行线性化处理，得到

(2)A-H接续服务

类似于H-A接续服务，当进港航班q∈F(O)与列车i∈I(T)接续，即1，则说明两者的接续时间(列车i在换乘站的出发时间与进港航班q的到达时间之差)大于等于最小的换乘时间t(A-H-low)，且小于等于旅客可容忍的最大换乘时间t(A-H-up)；否则，0。故存在约束为

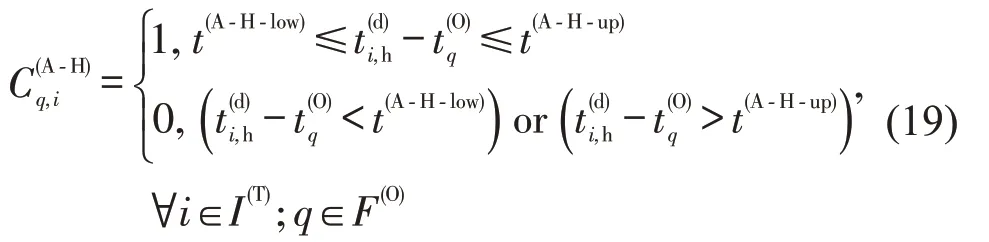
机场u所在地与车站s所在地组成的OD若可达需要满足以下3个条件：①由始发机场是u的航班q∈服务；②由在空铁换乘枢纽停站，且在s∈S(A-H)停站的列车i∈服务；③航班q∈与列车i∈的接续时间满足式(19)。可达变量与接续变量之间的关系为

式(20)等价于

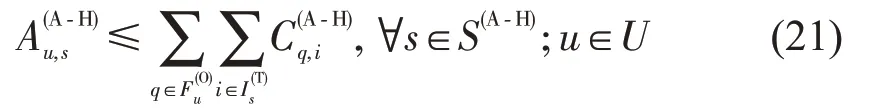
同理，对式(19)进行线性化得到

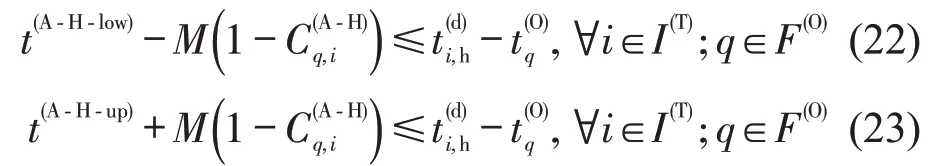
2.4.5 求解方法

模型为多目标整数规划模型，区别于普通时刻表优化模型，考虑列车与航班的接续关系和可达关系，增加了问题的复杂度。求解思路是基于分层优化思想，将多目标问题转化为单目标问题，单目标问题采用商业软件ILOG CPLEX求解。首先，计算在空铁换乘枢纽停站列车I(T)的时刻表，即以最大化Z1为目标，以式(3)～式(13)，式(16)～式(18)和式(21)～式(23)为约束，使用ILOG CPLEX求解列车I(T)的时刻表；然后，计算在空铁换乘枢纽不停站列车I(N)的时刻表，即在列车I(T)时刻表固定的前提下，以最小化Z2为目标，以式(3)～式(13)为约束，使用ILOG CPLEX求解列车I(N)的时刻表。

3 实例分析

3.1 相关参数

以石家庄正定机场及其高铁站作为空铁换乘枢纽研究对象，优化调整京广运输通道中北京-郑州区段下行方向高铁时刻表。选择2018年7月28日7:00-21:00间112列高铁的时刻表数据，其中，经停正定机场高铁站的列车数量为16 列，其他列车数量为96列。本文以关键OD作为研究对象，不考虑客流需求较少的车站和机场；同时，结合空铁联运优势运距，不考虑短途航班。因此，该案例中关键空铁联运OD 涉及10 个车站，96 个离港航班，36个目的机场，71个进港航班，26个始发机场。其他相关参数如表1所示。使用MATLAB R2015b调用ILOG CPLEX 12.5 求解器在8 G 内存、Intel i5 3.0 GHz的环境下进行编程测试案例。

3.2 优化结果

优化前，关键空铁联运可达OD 为160 个，H-A接续服务OD 数量为76 个，A-H 接续服务OD 数量为84 个。优化后，关键空铁联运可达OD 为181个，比优化前增加21 个可达OD，提高13.13%。其中，H-A 接续服务OD 数量为89 个，A-H 接续服务OD 数量为92 个。增加的可达OD 对如表2所示。总调整时间为1681 min，每列高铁在每个经停车站的平均调整出发时间为3.27 min。其中，列车I(T)平均调整出发时间为18.18 min，列车I(N)平均调整出发时间为0.90 min。ILOG CPLEX 总运算时间为4287 s。

3.3 灵敏度分析

对不同始发、终到时间窗进行灵敏度分析，测试时间窗的宽度和空铁联运可达OD 数量之间的关系。不同时间窗宽度取值结果如图2所示。

表1 相关参数Table 1 Parameters

表2 优化后增加的可达OD 对Table 2 AH intermodality accessible OD after adjustment of timetabling

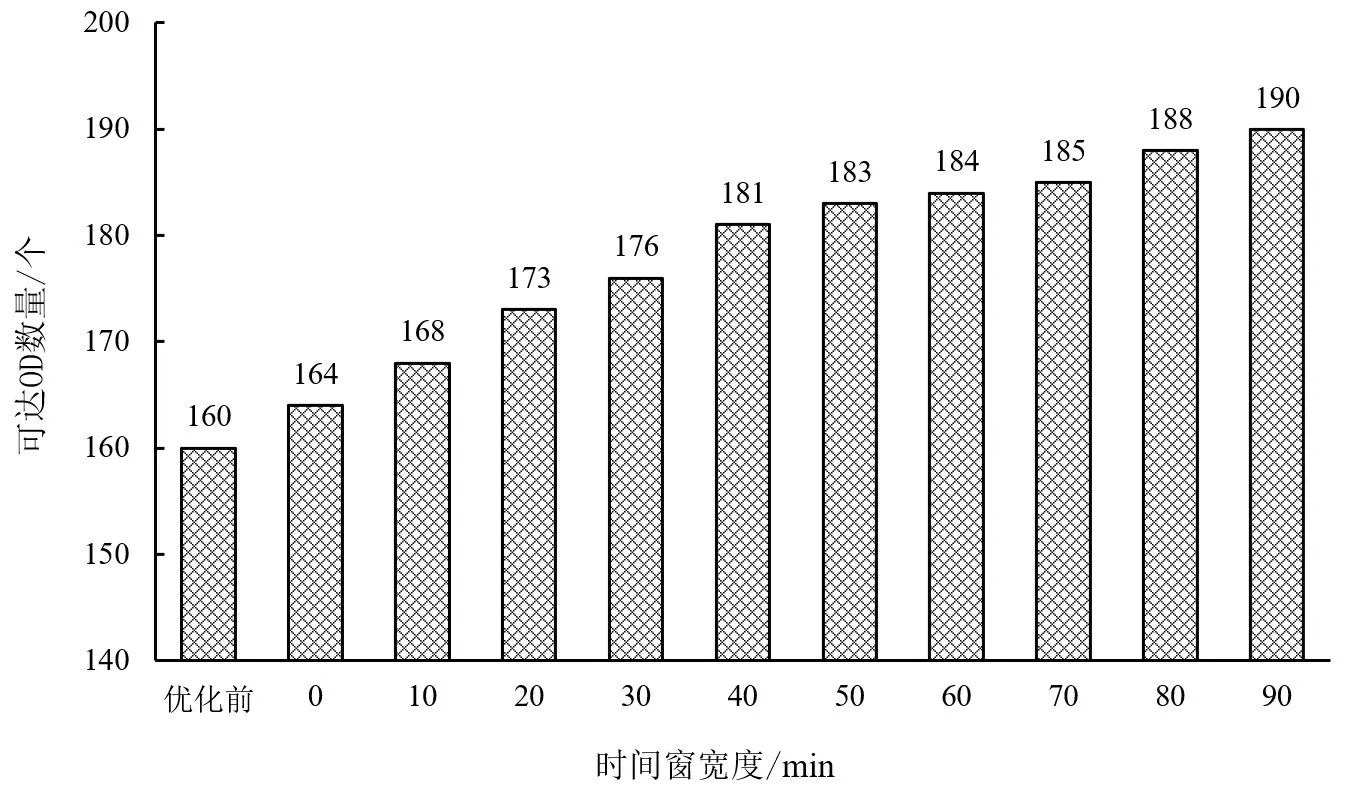
图2 不同始发、终到时间窗宽度对应的空铁联运可达OD 数量Fig.2 Number of AH intermodality accessible OD for different time window

由图2可知，随时间窗宽度增加，即随着列车可偏移原时刻表的时间范围增大，空铁联运可达OD的数量在不断增加。当时间窗宽度为0 min 时，即仅通过调整列车在不同车站的停站时间及运行时间，便可增加4个可达OD；当始发、终到时间窗扩大到90 min时，可达OD数量增加到190个，比优化前的时刻表增加30个。但是，时间窗的增加意味着调整后的时刻表比原有时刻表的偏移程度增加，一方面过大的偏移可能导致动车交路的改变，从而增加列车运行成本；另一方面可能影响原有已经培养的客流乘车习惯，进而影响客流量。

4 结论

为提高空铁联运服务质量，本文提出空铁联运OD 可达性约束，建立面向关键空铁联运OD 可达性的高铁时刻表优化模型。以石家庄正定机场为案例，利用ILOG CPLEX 在可接受的时间范围内求出最优解。结果表明，在始发、终到时间窗为40 min 的前提下，关键可达OD 数量增加21 个，比既有时刻表提升13.13%，时刻表总调整时间为1681 min，平均每列列车在每个停站的出发调整时间为3.27 min，说明模型在保证列车稳定性的同时能够有效提升空铁联运可达性。分析不同始发、终到时间窗灵敏度发现，空铁联运可达OD数量随着时间窗的扩大而显著增加，但有必要平衡增加可达OD数量与由此产生的运行成本之间的关系。