基于路段间转移概率的最优路径预测方法
李军,郭育炜,叶威
(中山大学,智能工程学院,广州510006)
0 引言
传统最优出行路径多是根据路段的交通阻抗计算获取,且城市道路中路段交通阻抗最具代表性的指标为出行时间,但出行时间极具不确定性。虽然交通大数据技术为道路阻抗的估算提供了支撑,但获取路段阻抗特别是交通拥堵状态下的阻抗仍有较大困难。另一方面,由于交通状态的复杂性,出行者的实际出行路径往往与利用阻抗计算出的路径有较大差异。因此,直接利用数据驱动的方式寻找最优出行路径逐渐成为研究热点[1]。
出行者位置转移的选择通常可以描述出行者在出行过程中的实际选择行为[2]。基于出行者位置转移的研究当中,基于Markov 及其改进模型的研究是较新型的方法,主要思想是以路网中的节点或路段为状态空间,出行者的行驶过程为状态间的转移,从而构建全局最优路径预测方法[3-6]。这些研究采用数据驱动方法,实现对出行者下一个位置的预测,取得了较高的精度;大多数研究利用较繁杂的机器学习过程,对寻找最优路径而言,其实现效率往往较低。城市中,人们对出行环境较熟悉,可假设历史出行数据当中隐含出行者对最优路径的选择,因此有学者基于特定条件下的历史出行轨迹,获取其转向规律并进行最优路径规划[7-8]。这些方法通过历史出行轨迹的某些规律或指标分析,实现路径预测。但在实际应用当中,存在有效轨迹选取方式不合理的问题:一是不同出行时段内的交通状况存在较大差异,对最优路径预测结果具有一定影响,应将其纳入考虑;二是数据样本量不足,并非所有车辆均可提供相应轨迹数据,且起点、终点数量众多,针对特定的起点和终点,完全匹配的路径数量不多,再考虑出发时刻的匹配,其数量更少,样本量不足以统计分析。
考虑城市道路拥挤网络多为通勤时段,出行者多会选择最优路径出行,考虑出行者认知的随机性,认为所面临的路网状态为“随机用户均衡(SUE)”,即在所有出行者均认为自身已选择最优路径的前提下,依据历史出行数据为特定起点与终点间的出行进行最佳路径的规划。城市出租车出行中,司机对道路网络都较为熟悉,可以假设历史行程当中被选择频率最高的就是最优路径。因此,本文提出一种基于路段间转移概率的最优路径预测方法,一方面避免路段阻抗的计算,另一方面考虑不同交通状况存在的影响,以及解决历史数据量不足的问题。包括有效轨迹集的构建,路段间转移概率的计算,以及最大概率路径求解算法的设计,并将最大概率路径作为最优出行路径的预测结果。最后通过广州市某个区域的出租车轨迹数据作为案例,验证方法的合理性。
1 基于路段间转移概率的最优路径预测建模
考虑典型的出行路径选择问题,在一个道路网络给定出行起点r与终点s,以及出发时刻,本文利用数据驱动方式,为出行者寻找最优的出行路径。通过计算路段间的转移概率,构建出行者对路段选择的Markov过程,计算路径被选择的概率,将最大概率路径作为最优路径的预测结果。最优路径的预测主要包括两个部分:一是从历史数据中提取有效轨迹,统计获取路段间的转移概率;二是设计基于路段间转移概率的最优出行路径预测算法。
1.1 有效轨迹提取及转移概率计算
选取有效轨迹时面临两方面问题。其一,不同时间段中,路网存在不同程度的拥堵状况,交通特性与路段阻抗具有不同变化,并非所有历史数据与现时的最优选择一致;其二,在多数情况下,起点r与终点s间的轨迹数量极少,不足以进行分析。
对于出行时段问题,根据城市路网交通特性,将一天中的时间划分为早高峰、晚高峰与非高峰(早晚高峰除外的其他时段)这3个时段。根据出行时间点,选取对应时段的轨迹集。为解决历史数据不足问题,将历史数据的选择从给定的点扩展到其出行小区,认为同一个交通小区中所产生的出行具有相似特性,通过区域划分扩大轨迹数据的选取范围,将起点所在区域前往终点所在区域的轨迹作为轨迹集。
具体步骤为:将研究范围内的交通路网划分为若干个区域,并判断起点r与终点s所在区域,分别记为区域O与区域D,如图1所示。

图1 区域划分示意图Fig.1 Diagram of area division
在所有轨迹中,提取同时满足出行时段与出行区域条件的历史轨迹:①轨迹行程所处时段与给定的出行时间所处时段一致;②轨迹行程由区域O前往区域D。将筛选所得轨迹构建为有效轨迹集,记为ΓOD。数据虽未能覆盖总体样本,但其数据具有代表性。其一,通过从时间、空间两个维度上扩大范围获取更多数据量,不影响方法有效性的验证;其二,本文采用的数据为城市出租车,出租车司机是对交通路网熟悉程度较高的群体,其选择具有代表性;其三,采用数据跨越时段较长,同时按照不同时段对数据进行划分,大量浮动车数据具有随机性,短时间采样不均匀性造成的误差,可以通过长时间的历史数据来弥补。
将路网表示为网络图G=(V,A),其中,A表示网络中的路段集合,A={al|l=1,2,…,Ia},al表示一个路段,Ia为网络中路段数量;V表示网络中的节点集合,V={vi|i=1,2,…,Iv},vi表示一个节点,Iv为网络中节点数量。若路段al分别以vi1、vi2为起点、终点,i1,i2∈[1 ,Iv] ,记为al=(vi1,vi2)。
将网络中的路段作为Markov 链的状态空间,路段间转移概率定义为Markov链的转移概率。统计ΓOD中的轨迹,获得路段间转移概率及起始路段的选择概率。
假设两个路段al1与al2,l1,l2∈[ ]1,Ia,则路段al1到al2的转移概率为

式中:Fl1为路段al1的所有下游路段集合;为轨迹集ΓOD中,先后依次经过路段al1与路段al2的轨迹数量;为轨迹集ΓOD中,经过路段al1的轨迹数量。
因轨迹起点是点而非路段,故需要计算从起点r出发,选择每个起始路段al(l∈[1 ,Ia])的概率为

式中:为轨迹集ΓOD中,先后依次经过r与路段al的轨迹数量;NrOD为轨迹集ΓOD中,经过r的轨迹数量。
如图2所示,假设由起点r出发的起始路段有a1、a2、a3且由ΓOD统计得到先后依次经过节点r与各路段的轨迹数量比例为0.2 、0.7 、0.1,则;假设路段a2的下游路段有a5、a6、a7且由ΓOD统计得到先后依次经过路段a2与各下游路段的轨迹比例为0.4 、0.5 、0.1,则
1.2 最优出行路径预测方法
对r与s间的某一条路径,定义其选择概率为:起点r的起始路段概率与每相邻两个路段间转移概率的乘积。假设L:r →al1→al2→…→alx-1→alx →s()al1,al2,…,alx∈A是r与s间的一条路径,则L的选择概率pL为

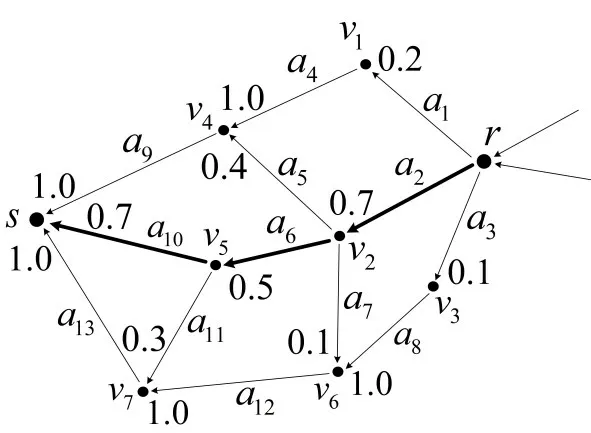
图2 路段间转移概率Fig.2 Link-to-link transition probability
例如,图2中路径L1:r →a2→a6→a10→s的选择概率为

依据上述定义,在r与s之间的所有路径中,必然存在一条选择概率最大的路径。本方法将r与s之间概率最大的路径作为最优预测路径。参照Dijkstra 算法求解最短路径问题的过程,设计最大概率路径求解算法如下(此处只以求解r与s两点间的最大概率路径为目标)。
定义算法涉及符号:Τ(vi)为节点vi的临时标号,表示r到vi的临时性最大概率;Ρ(vi)为节点vi的永久标号,表示r到vi的确定性最大概率;SΤ为具有临时标号的节点集合;SΡ为具有永久标号的节点集合;λ(vi)为从r到节点vi的最大概率路径上,vi的前一个节点。
Step 0 初始化。令SΤ=V,SΡ=∅;对每一个vi∈V,令Τ(vi)=0,λ(vi)初始时为空值。
Step 1 寻找每个节点vj(j∈[1,Iv])满足(r,vj)∈A;记(r,vj)=aj′,令vj的临时标号
Step 2 在SΤ中寻找节 点vq(q∈[1,Iv])满足,为vq赋予永久标号Ρ(vq)=Τ(vq),并令SΡ=SΡ⋃{vq} ,SΤ=SΤ-{vq} 。
Step 3 如果vq=s,进入Step 5;否则,进入Step 4。
Step 4 记[λ(vq),vq]=aq′。寻找vq的每个下游节 点vt(t∈[1 ,Iv] 且满足(vq,vt)∈Fq且vt∈SΤ),若,其中,at′=(vq,vt),则更新Τ(vt)的 值 为,且 令λ(vt)=vq;若,则不更新Τ(vt)和λ(vt);若不存在vt满足(vq,vt)∈Fq′且vt∈SΤ,则令Τ(vq)=0 。返回Step 2。
Step 5 由s向r回溯,依次搜索节点vj1,vj2,…,vjy(j1,j2,…,jy∈[1 ,Iv])满足vj1=λ(s)、vj2=λ(vj1)、…、vjy=λ(vjy-1)、r=λ(vjy),则最大概率路径为:r →vjy →vjy-1→...→vj2→vj1→s。
2 案例分析
以广州市为例验证预测路径的合理性。为全面验证方法合理性,考虑区域划分大小,不同时间段,起终点位置3 个因素的影响,分不同情况进行实验。①对划分区域的粗化与细化分别验证,共2种情况;②对早高峰、非高峰、晚高峰时段分别验证,共3种情况;③交换起点r与终点s的位置分别验证,共2 种情况。针对3 方面因素不同情况的组合,进行12次验证。
随机给定位于广州市天河区的一对起终点(相距约5 km)。依据以下规则对区域进行粗划分与细划分:不分割城市行政区界,行政区界内不分割主要道路、公路和河流等地理交通要素,并综合考虑所获取数据量的充足性,图3为区域划分结果,其中,r与s所在区域分别记为O、D。早高峰、非高峰、晚高峰时段分别为7:00-9:00、12:00-14:00、17:00-19:00。在2014年2月24日-3月21日的工作日提取与出行时间相对应时段内的出租车历史轨迹,选取由区域O前往区域D的轨迹,得到有效轨迹集ΓOD。
统计轨迹集ΓOD,得到轨迹所包含的路段,r的起始路段选择概率,路段到路段的转移概率,建立路径选择的Markov过程。根据最优出行路径预测方法,求解得到r与s之间的最大概率路径。
2014年2月24日-3月21日期间工作日内与出行时间相对应时段的出租车轨迹当中,选取r与s之间的轨迹,作为验证轨迹。对验证轨迹按照被选择的频率大小进行排序,此处仅统计频率最高的4条轨迹。12 次实验的预测路径与相应的验证轨迹如图4所示,每一次实验结果如表1所示。
由表1可得,预测路径有7 次实验与频率最高的轨迹一致,有4次实验与频率第2的轨迹一致,有1 次实验与频率第4 的轨迹一致。实验4 只预测出频率第4的轨迹,这是因为该次实验中验证轨迹样本量不足(只有20多条)。频率第2的轨迹数量仅比频率第4 的轨迹多1 条,说明验证数据量不足导致结果出现较大偶然性。

图3 区域划分Fig.3 Division of areas

图4 路径编号Fig.4 Identifier of routes
本文以区域之间数据预测起终点的最优出行路径,本身为基于数据驱动的估算方法,计算结果为频率第2轨迹属正常结果。表1结果说明,本方法对所采集数据产生的结果而言具有显著的有效性。
除验证预测结果的总体准确性,同时比较分析单方面因素产生的影响,如表2所示。
由表2可知,单方面因素影响如下:
(1)区域划分大小不同,预测准确性均较高、差异较小,表明区域划分大小对预测准确性影响较小。
(2)时间段不同,非高峰、晚高峰时段的预测结果准确性较高,早高峰时段略低,表明不同时间段内的预测准确性具有一定差异。
(3)起终点位置不同,预测准确性均较高,差异较小,表明不同起终点位置对预测准确性影响较小。

表1 预测路径与验证轨迹比较Table 1 Comparison between predicted route and verified trajectory
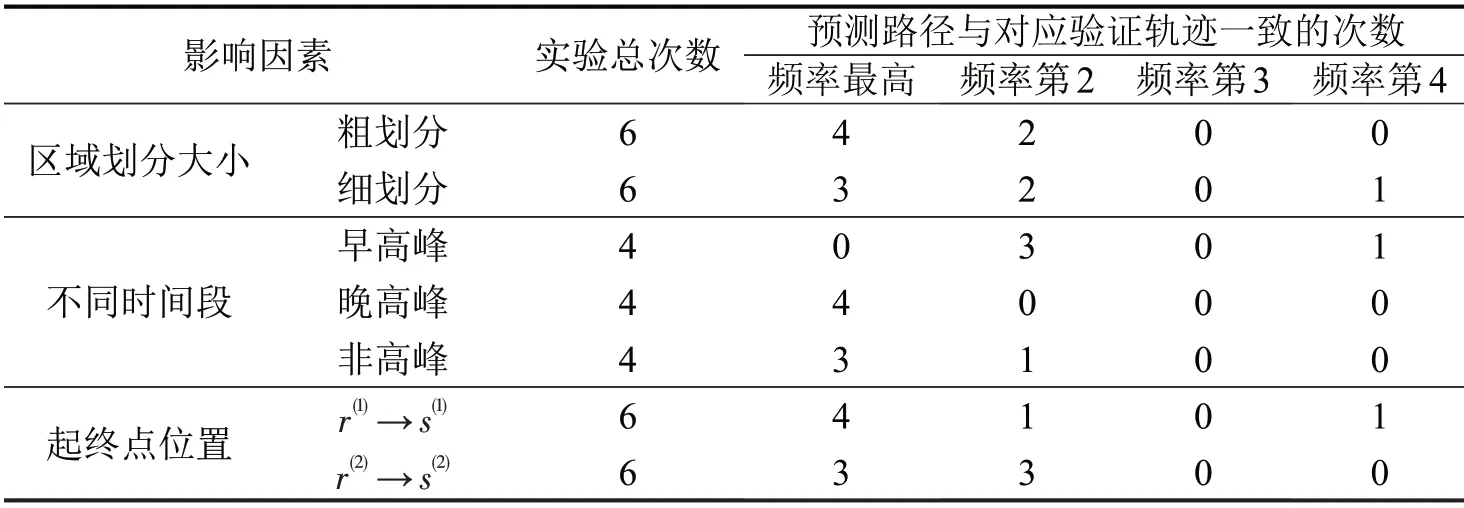
表2 单方面因素结果比较Table 2 Comparison of one-sided factors
3 结论
本文提出将数据驱动、出行时段与出行区域划分相结合的最优出行路径预测方法,解决了路段阻抗计算困难和数据量不足的问题,结果总体准确性高,且具有数据易获取,执行过程简便的优点,体现出在已有采集数据情况下的有效性。此外,分析各方面因素的结果表明,不同区域划分大小和不同起终点位置对预测准确性影响较小,不同出行时间段对预测准确性具有一定的差异性影响。因此,利用本文方法预测最优出行路径时,应注意时间段的合理划分,而对于区域划分则可适当扩大,以获取较充足的数据量。
另外,从“系统最优”层面来看,本文便于理解出行者的行为,挖掘出行者出行规律,对交通管理与规划的实行措施具有一定价值。

