基于特征优选和GA-SVM的滚动轴承智能评估方法

周建民， 王发令， 张臣臣， 张 龙， 尹文豪， 李 鹏

(华东交通大学 载运工具与装备教育部重点实验室，南昌 330013)

轴承是机械结构中的关键部件，状态监测和故障诊断是保证机械设备正常运行的关键。轴承故障诊断过程主要包括故障特征提取和故障分类[1]。当轴承发生故障时，振动信号的频带能量会发生变化。如果能够提取出轴承的频带信号特征，就可以进行轴承故障分类。因此，有效地提取故障特征是故障诊断的关键。

滚动轴承故障研究主要以振动信号的研究为主，振动信息具有非线性和非平稳特点[2]，尤其是运行中萌生的早期故障，特征信息微弱，同时受到机械设备产生的强噪声干扰，给故障诊断带来困难[3]。

Gai等[4]利用经验模态分解(empirical mode decomposition，EMD)对已知状态下的轴承振动进行分解，再通过奇异值分解(singular value decomposition，SVD)获得固有模态函数(intrinsic mode function，IMF)分量的奇异值作为特征向量，提出了基于EMD-SVD和模糊神经网络的轴承退化评估方法，有效地分析轴承的性能退化情况。Malik等[5]结合EMD和人工神经网络(artificial neural network，ANN)建立轴承故障诊断模型，比较EMD特征输入到不同ANN分类器的效果，最后得出了不同ANN模型在轴承故障诊断中的性能特点。但EMD分解过程中存在过包络、欠包络、模态混淆、端点效应等问题[6]。

为了解决EMD的问题，Wu等[7]引入噪声辅助分析，提出集成经验模态分解(ensemble empirical mode decomposition，EEMD)，有效地抑制了模态混叠等问题。EEMD作为一种新型自适应、近似正交的分解方法，同时适用于非线性、非平稳信号的分析。Chen等[8]利用EEMD将信号分解为固有模态函数(intrinsic mode functions，IMFs)，然后利用希尔伯特平方解调(hilbert square demodulation，HSD)对选定的IMFs进行解调，用于风力机齿轮箱故障诊断。陈法法等[9]将EEMD和信息熵结合，用EEMD能量熵来提取轴承故障特征，有效获得轴承振动信号的特征分布类型。鉴于EEMD在信号分析中优越性和早期弱信号的检测能力，本文将其与信息熵结合，通过EEMD分解轴承振动信号获得IMF，计算IMF的能量熵比作为特征，充分刻画轴承振动信号的细节信息。

基于人工智能(artificial intelligent，AI)的早期故障诊断作为一种新兴的工业应用和故障识别的有效解决方案，越来越受到学术界和工业界的重视。其通过机器学习技术，可以有效地克服对研究人员专业知识要求较高的局限性。在基于AI的早期故障诊断方案中，最常用的模型有隐马尔可夫(hidden markov model，HMM)、支持向量数据描述(support vector data description，SVDD)、支持向量机(support vector machine，SVM)、高斯混合模型(gauss mixture model，GMM)和ANN。

Wang等[10]利用SVM做分类器，通过EMD-SVD求解轴承振动信号特征，输入到SVM模型中获得故障分类结果。Zhang等[11]利用特征空间中簇间距离优化SVM，对电机轴承进行故障类型分类，得到良好的分类效果。陈龙等[12]提出基于单层稀疏自编码器学习和SVM的轴承性能退化评估方法，成功得到性能退化趋势。上述对轴承进行故障诊断或性能退化评估的研究都取得了良好的结果，但是其研究内容仅局限于仿真故障数据而忽略了实际轴承损坏的各种工况。因此本文提出基于SVM的智能评估方法，使用轴承真实数据进行测试，既能诊断不同的轴承故障类型，也能对轴承进行性能退化评估，判断早期故障点。

本文使用EEMD提取轴承全寿命周期数据的特征，利用信息熵处理IMF分量，获得IMF分量能量熵比。为了充分提取轴承的有效特征，使用常用的时域计算方法提取数据的时域特征。利用相关性、单调性和鲁棒性有效的选择退化特征，得到最终的特征向量。采用遗传算法(genetic algorithm，GA)优化SVM参数，将三种不同类型故障轴承分为正常、退化和失效样本，输入模型中训练并获得最优参数。通过定义新的退化指标，评估轴承性能退化状态，确定轴承早期故障点。通过未使用的失效数据验证方法在实时监测中的应用。最后通过对比验证确定方法的有效性和优越性。

1 特征提取及选择

1.1 时域特征提取

准确评价轴承性能退化特征提取的概念是实现轴承状态在线监测平台的关键。研究了从滚子轴承振动信号中提取的各种原始特征。传统的统计特征是表征轴承振动信号发生故障时变化的有力工具。当轴承发生故障时，振动信号的时域特征会随着故障的位置、大小而发生变化，因此时域特征可用于表征轴承的工况。本文选取的时域特征如表1所示。

表1 时域特征计算公式Tab.1 Calculation formula of time-domain features

1.2 集成经验模态分解

EMD是Huang等[13]提出的一种新的自适应方法，适用于非线性分析和非平稳信号处理。在EMD中，一个信号可以分解为多个IMF和一个残差。但在实际应用中，由于其固有的模态混叠等问题，大大的限制了其实用性能。因此，Wu等和Huang等提出的集成经验模态分解，有效抑制消除EMD中的模态混叠，得到的IMF分量更加真实客观的反映信号的物理信息。具体算法过程见参考文献[14]。

分解所得最终原始振动信号表示为

(1)

式中：cj(t)为EEMD分解后所得的第j个IMF分量;si(t)为分解所得残差和的均值。

1.3 EEMD能量熵

信息熵作为系统不确定性程度的描述已经在特征提取和信号处理方面得到广泛的应用。当系统中的不确定性信息越多，则对应的熵值越大。用信息熵描述定量信号不确定性与复杂程度的统计特性具有稳定性好、抗噪能力强的特点。故障轴承的振动信号的频率成分和各频率段内信号的幅值能量会发生变化，因此结合EEMD和信息熵理论可以更为详细的解剖轴承信号的退化信息。构造EEMD 能量比的具体步骤见参考文献[15]。

EEMD能量熵的计算公式为

(2)

式中：Hen为第i个 IMF分量的能量熵;pi=Ei/E为第i个IMF分量占总能量的百分比。

由其他轴承诊断研究可知，EEMD特征提取考虑的IMF分量个数越多，后面的IMF分量对轴承诊断的作用越小。因此，本文只考虑前10个IMF分量。

1.4 特征选择

上述所提取的一些退化特征可能与轴承的退化现象无关，因此，他们可能无法在轴承发生故障之前指示变化。为了提高性能退化评估的准确性和有效性，需从提取的退化特征中进行选择，并通过融合所选择的退化特征来构建轴承性能的健康指数。

合理的退化特征与轴承退化处理具有良好的相关性，单调递增或递减，对异常值的鲁棒性都是轴承特征选择考虑的条件[16]。对提取的退化特征的单调性、鲁棒性和相关性进行估计，得到退化特征子集。退化特征的选择过程如下。

(1)采用平滑法将提取的退化特征分解为均值趋势和随机部分

fea(t)=feaT(t)+feaR(t)

(3)

式中：fea(t)为t时刻的退化特征值；feaT(t)为趋势部分的数值；feaR(t)为随机部分的数值。

(2)特征选择指标的计算公式为

(4)

(5)

(6)

(3)相关性是特征与时间线性关系的度量；单调性评价特征变化趋势的一致性；鲁棒性反映特征对异常值的容忍度。由式(4)～式(6)可知，三个指标均在[0,1]内，与特征的性能呈正相关。为了综合考虑三个指标，提出加权线性组合作为退化指标选择准则，计算公式为

Cri=ω1Corr+ω2Mon+ω3Rob

(7)

式中:ω1=0.2,ω2=0.5,ω3=0.3为指标的权重，这是由指标对轴承退化的贡献程度决定的[17]。

由于退化指标的尺度不一致，数据直接融合造成很大的失真，容易导致特征的错误选择。因此，需要对得到的各个指标的数据进行标准化。标准化计算为

(8)

2 GA-SVM

2.1 遗传算法理论

遗传算法是一种全局优化概率搜索算法[18]，因其具有鲁棒性强、适用性广，操作简单等优点而得到广泛的应用。其主要思想是选择合适的适应度函数，先产生初始种群，通过编码产生染色体，仿照自然界的淘汰机制对个体进行选择、交叉和变异等操作。最后得到满足条件的个体进行反编码得到最优解。

2.2 支持向量机理论

SVM是一种小样本分类方法，这种方法通过构建最优超平面，使得超平面两侧的不同类样本的距离最大化。因其在解决非线性高维空间问题上的优越性而被广泛应用于模式识别、函数逼近、概率密度估计、故障诊断等领域。支持向量机的分类模型为

(9)

2.3 GA优化SVM实现过程

使用SVM处理离散变量和引入核函数中需要确定惩罚因子c和核函数参数g，两者的选择直接影响了SVM的分类精度和泛化能力。惩罚因子c与数据的拟合程度成正比关系，c取值越大则数据拟合程度越高。核函数参数g决定分类效果，g的取值过大则会降低分类效果。

SVM参数确定往往是通过交叉验证思想下使用网格法寻找最优惩罚因子和核函数参数。为了克服网格法在大范围内寻找最优参数的局限性，采用遗传算法来搜索最优参数。优化具体步骤见参考文献[19]，其中，c∈[0,100]，g∈[0,100]。

3 试验及结果分析

3.1 试验介绍

实验数据采用美国辛辛那提大学智能维护系统中心轴承疲劳寿命试验台数据[20]。试验台如图1所示。

图1 滚动轴承加速疲劳寿命试验台Fig.1 Rolling bearing accelerated fatigue life test bench

试验台的主轴上装有4个型号为Rexnord ZA-2115的双列滚子轴承，如图2所示，轴承每排包含16个滚子，节圆直径71.5 mm，滚筒直径为8.4 mm，接触角15.17°。通过对轴和轴承施加径向载荷约为2 721.6 kg。转速保持在2 000 r/min。采用NI DAQ-6062E数据采集卡，采样频率为20 kHz，间隔10 min采集一次数据，每次采集时间为1 s，采样长度为20 480个点。加速度传感器型号为PCB353B33，分别安装在主轴的水平方向和垂直方向。

图2 Rexnord ZA-2000轴承系列Fig.2 Rexnord ZA-2000 bearing series

每次试验有4个轴承进行测试，当某一个轴承损坏时，停止实验，保留实验数据。整个数据集描述的数据内容为轴承从健康运行到失效的整个实验振动信号变化过程。测试结束后在轴承的磁性插头上发现大量的金属碎片，证明轴承已损坏。失效的轴承部件如图3所示。

图3 失效轴承部件图片Fig.3 Pictures of failedbearings parts

选择三种不同部件失效的轴承作为样本：第一种为外圈失效样本，样本总数为984个，其中最后两个样本波形已失真，因此样本总数为982个；第二种为内圈失效样本，样本总数为2 156个；第三种为滚子失效样本，样本总数为2 156个。

将样本分为正常样本(H)、外圈退化样本(DOR)、外圈失效样本(FOR)、内圈退化样本(DIR)、内圈失效样本(FIR)、滚子退化样本(DR)、滚子失效样本(FR)。样本总数为5 294，其中正常样本临近退化样本之间会有重叠部分，轴承出现故障是缓慢形成的，而不是一次性出现大的缺陷，因此存在这一重叠带。同理，退化样本临近失效时也会存在重叠部分，为了避免模型在这一重复地带之间判断失误，去掉重叠带数据，将样本总数减少到3 334个。各类样本设置的SVM标签和样本数如表2所示。

表2 样本个数及SVM标签Tab.2 Number of samples and SVM tags

3.2 特征选择结果分析

按表1所列的顺序提取时域特征，编号为1～11，同时提取EEMD能量熵总和作为编号12，提取IMF分量能量熵比作为编号13～22。

分别提取三种不同故障的轴承特征，计算各特征的相关性、单调性和鲁棒性分别如图4所示，图4中曲线代表三种不同故障的轴承在同一个特征下的均值。

图4 三种不同故障的轴承的特征分析图Fig.4 Feature analysis of three bearings with different faults

在相关性对比当中，外圈失效轴承会有相对较高的相关性，所提取的时域特征和EEMD能量熵都有个别较高的相关性系数存在。在单调性中时域特征占大的优势，但单调性值的波动区间远小于相关性和鲁棒性值的波动区间。除了第4个特征和第22个特征之外，其余特征都具有较高的鲁棒性。综合考虑三个指标，计算综合指标Cri，并进行标准化，结果如表3所示。

表3 不同特征的综合指标Cri值Tab.3 Comprehensive Cri values of different features

为了选择最优特征子集，设置选择特征的阈值为0.6，对综合指标进行排序，如图5所示。选择特征综合指标Cri>0.6的特征，特征编号分别为01，15，07，12，06，11，13，16，03，14，02。保留所选的特征作为最优特征子集。

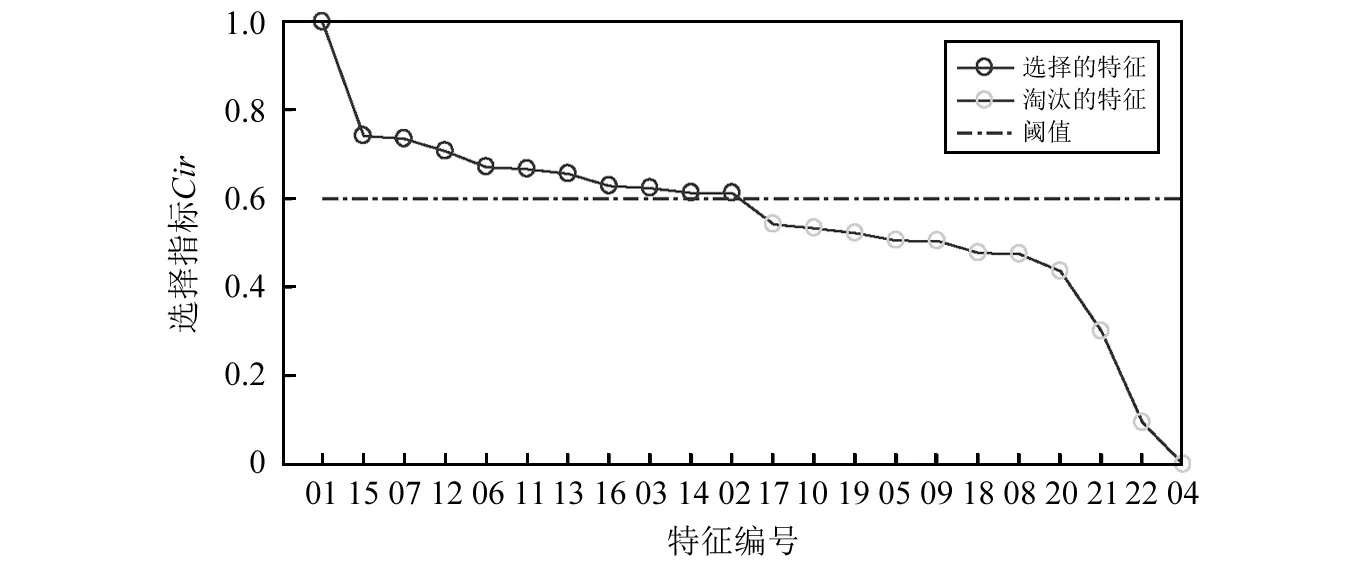
图5 特征综合指标选择Fig.5 Selection of comprehensive index of features

3.3 基于SVM的早期在线检测模型及结果分析

GA优化结果得出最优参数为c=23.85，g=1.787 5，保留最优参数，输入SVM中作为测试模型的参数。检测轴承的性能退化情况，使用退化指标(degradation index, DI)来评估轴承的退化状态。退化指标的具体计算方法如下：

步骤1获取轴承全寿命数据。

步骤2提取数据的特征并进行特征选择。

步骤3将特征分为训练样本和测试样本，训练样本训练SVM模型并通过遗传算法找到最优的参数。

步骤4定义退化指标Di(1)=0。从第二个样本开始，当SVM输出标签为1时，判断轴承属于健康状态Di(i)=Di(i-1)+0；否则Di(i)=D(i-1)+1；Di为0表示健康状态，Di越大则故障越严重。其中，i为全寿命周期样本数据的第i个时刻数据。

通过计算模型分类精度评估模型分类的准确性，其中，模型分类精度计算公式为

使用三种不同故障类型的轴承全寿命周期数据进行测试，故障智能评估模型可通过标签智能识别出故障的类型。再根据退化指标定义，绘制出轴承性能退化评估曲线，测试结果如图6～图9所示。

由图6可知，外圈故障检测早期故障点为第533个样本，即第5 330 min，而第533个样本到第911个样本为轴承退化阶段，第911个样本之后，样本标签发生变化，轴承为严重退化至失效阶段。在该阶段轴承已经无法使用。通过评估图形可对比，早期曲线为直线，模型输出标签为1，第533开始出现标签2，后期在接近800时出现直线情况，输出为标签1，即诊断失误情况，但并不影响曲线整体上升的趋势，通过模型输出标签与实际故障情况对模型分类精度进行计算，可得外圈故障分类精度为98.07%。

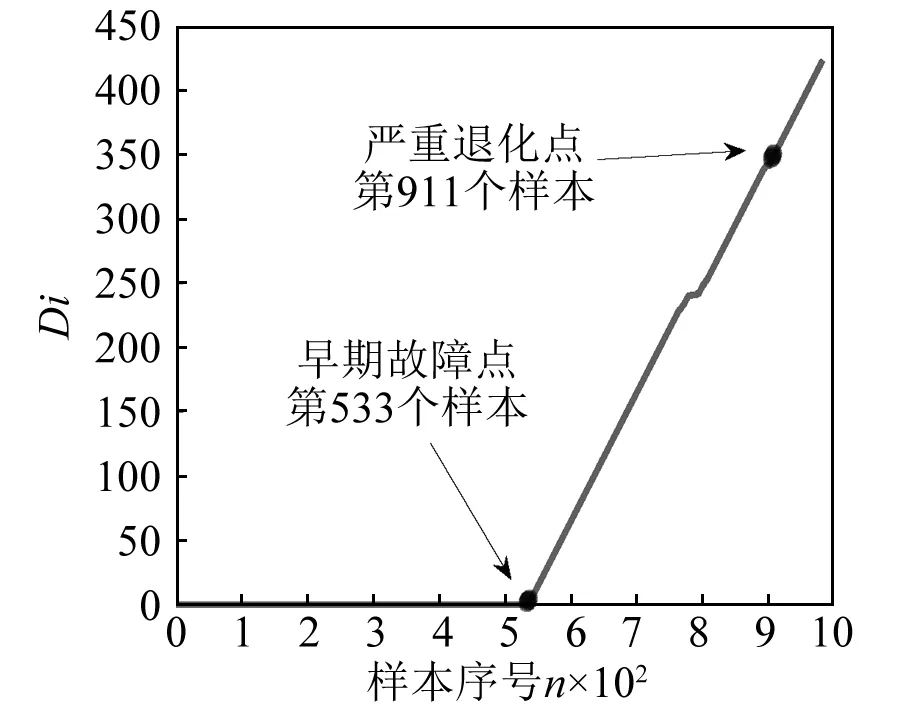
图6 轴承外圈故障数据评估结果Fig.6 Failure data evaluation results of bearing outer ring

从图7可得，内圈故障的早期故障点为第1 635个样本，即第16 350 min，轴承退化阶段为样本1 635～2 084。第2 048个样本之后，轴承严重退化。同理，通过对模型分类精度进行计算，内圈故障分类精度为96.29%。

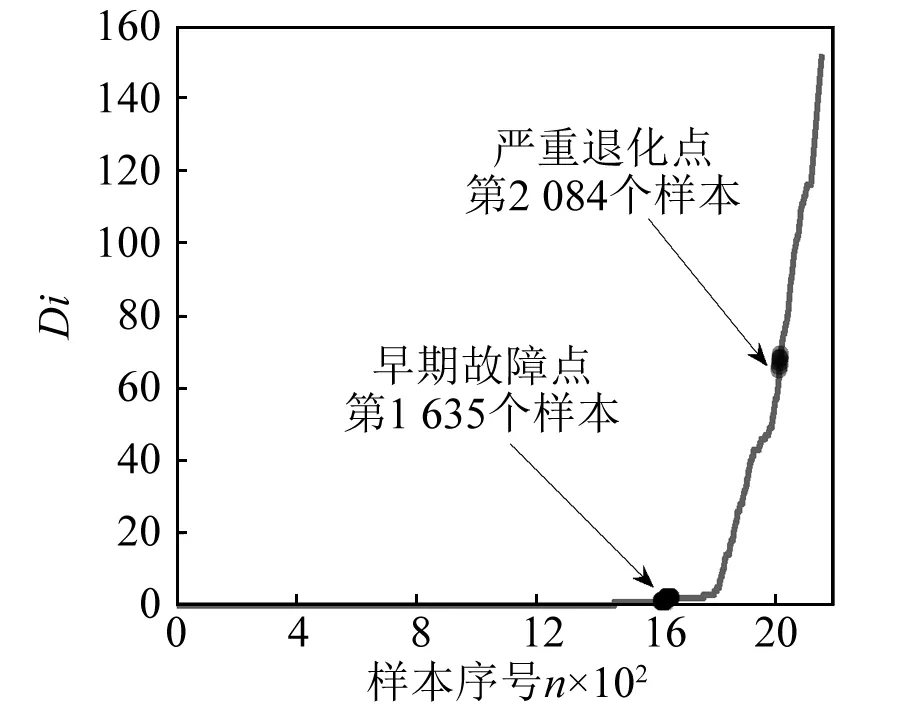
图7 轴承内圈故障数据评估结果Fig.7 Failure data evaluation results of bearing inner ring

由图8分析可得，轴承滚子故障数据的早期故障点为第1 438个样本，轴承退化阶段为1 438～2 105，轴承严重退化至失效阶段为2 105～2 155。滚子故障数据分类精度为98.7%。

图8 轴承滚子故障数据评估结果Fig.8 Failure data evaluation results of bearing rollers

在实际工程应用中，方法的使用需要基于数据驱动，因此需要获得同类轴承的历史全寿命周期失效数据。通过历史失效数据训练模型后，可直接在工程中实时监测轴承的性能退化状态。为了进一步评估，以辛辛那提大学提供的第三套数据作为测试样本，轴承与训练的轴承为同类轴承，数据样本共6 324个，轴承振动信号采集原始图如图9(a)所示，最终失效结果为轴承内圈故障。本文方法所得的评估结果如图9(b)所示，早期退化点为第6 163个样本，这与振动信号振幅增大所在位置相近。严重退化点为第6 244个样本。所得样本标签为内圈退化和失效，与实际失效结果一致，这一结果证明了该方法在实际工程监测中的有效性和方法的鲁棒性。

图9 测试数据评估结果Fig.9 Evaluation results of test data

3.4 结果对比与验证

为了验证本文提出的智能评估方法的优越性，对比其他方法如表4所示。

表4 方法对比Tab.4 Method comparison

通过对比可得，本文所用方法在同类型文章中具有更高的平均分类准确率，且能判断轴承的退化状态。而其他文章在有高故障诊断率的同时，无法评估轴承退化状态，其主要缺点是采用仿真数据进行试验，通过加工不同直径和深度的轴承故障来进行测试，但在实际工业中轴承的故障是反复磨损，逐渐扩大的。本文使用反映轴承动态响应的真实数据进行测试，测试结果更符合工程应用。

对比方法的性能退化评估的优越性与早期故障检测的准确性，以轴承外圈故障数据为例。峭度是工程中常用的监测参数，其曲线突变能及时反映轴承的状态，因此能判断早期故障点。基于峭度的轴承性能退化评估曲线如图10所示。

由图10可得，轴承的峭度曲线在第566个样本有小的突变，后缓慢上升，直到第647个样本之后才有一个大的突变。而不论是第566个样本还是第647个样本的判断，都比基于GA-SVM的智能评估模型判断的早期故障点要晚，这在工业的决策中是不允许的。而在第970个样本后峭度曲线直线上升，表示轴承失效，比实际判断晚了59个时刻，即590 min。

图10 外圈故障轴承全寿命周期内峭度曲线Fig.10 Kurtosis curve of the outer ring fault bearing life cycle

由前期研究成果可得该外圈故障数据的包络谱分析结果如图11所示。

图11 早期故障样本与无故障样本包络解调图Fig.11 Envelope demodulation diagrams of early fault and faultless samples

分析图11可知，在第533个样本中，谱峰出现在230 Hz,461 Hz和691 Hz，与ZA-2115轴承外圈故障特征频率236 Hz相近，谱峰所在频率与轴承外圈特征频率存在差异的根本原因为存在滑移效应[22]。而在第532个样本中则没有相应的峰值，对第532个样本之前的样本进行包络谱分析得出同样的结果，因此可确定第533个样本为早期故障点出现的样本。因此基于GA-SVM的滚动轴承智能评估方法得出初始故障结果与验证结果一致。

4 结 论

提出了一种基于特征优选和GA-SVM的智能评估模型，能准确识别故障类型，输出轴承性能退化指标，判断早期故障点，为设备的维护提供理论依据。

(1)相对于EMD特征提取方法，EEMD解决了EMD所面临的模态混叠、端点效应等问题，结合EEMD和信息熵能更加精确地提取轴承的退化特征。

(2)结合考虑相关性、单调性和鲁棒性的特征选择指标，可以有效剔除与轴承退化现象无关的特征，通过加权线性组合融合指标，最终确定综合指标大于0.6的特征为选择的特征。

(3)使用GA参数优化SVM参数，获得惩罚因子c和核函数参数g最优值。实验结果表明，基于GA-SVM的轴承故障智能评估方法的平均分类准确率达到97.69%。

(4)定义新指标，在智能识别故障的同时，能确定轴承早期故障点，绘制分析轴承性能退化评估曲线。通过三套不同故障类型的轴承全寿命数据和一套未使用的失效数据验证方法的可行性。