拉-弯-剪复合作用下型钢混凝土柱抗震性能研究及损伤量化分析

邓 宇， 孙仁中， 张 鹏， 李真真

(广西科技大学 土木建筑工程学院，广西 柳州 545006)

国内外学者对型钢混凝土的各种良好受力性能进行了广泛研究，从目前来看研究主要针对型钢混凝土抗弯性能、抗剪性能、以及节点的抗震性能[1-5]。但在拉弯剪复合受力状态下型钢混凝土柱的抗震性能，在各国文献中少有提及。我国《建筑抗震设计规范》[6]通过最大位移角把结构进行了抗震性能破坏等级划分，但缺乏更为详细的型钢混凝土受拉构件的量化指标。本文参考相关文献[7-10]，基于能量守恒原理分析了拉弯剪复合受力状态下型钢混凝土柱的损伤特性，利用损伤指数更为直观的对其进行破坏等级划分。

在地震荷载作用下，建筑物中受拉构件的轴心将与拉力作用点产生一定的偏心距，因此出现偏心受拉的情形，并且在此情况下，其通常是复合受力状态。比如：型钢混凝土桁架转换层受拉腹杆受水平地震作用时，轴向拉力作用点将与截面中心产生偏心距，同时构件还受弯矩和剪力的影响，为拉弯剪复合受力状态，并且相对于受压腹杆，受拉腹杆更易产生损伤。因此，鉴于上述在拉弯剪复合受力情况下的型钢混凝土柱的抗震性能及损伤量化评定是一项亟待解决的基础性问题。

从目前国内外研究情况来看，Minami等[11]通过把轴拉比、锚栓强度和锚栓的锚固方法等作为试验的研究参数，对非埋入式型钢混凝土柱脚在拉弯作用下进行试验研究，证明在试验极限抗弯承载力计算中累加强度法的合理性。孙建渊等[12]通过对9个后张预应力钢骨混凝土拉弯梁进行静力模型试验研究，得到挠度曲线等力学性能指标，为制定有关规范提供了参考。邓宇等[13]对15根预应力型钢混凝土柱进行单调加载试验，得到了其承载力计算公式及影响因素。上述可知，国内外缺少对拉弯剪复合受力情况下的型钢混凝土柱的抗震性能及损伤量化评定，因此有必要在此方面展开研究。

在地震作用下，普通混凝土构件受偏心拉力时，受拉区易出现裂缝。通过加入型钢形成型钢混凝土构件，可以有效的提高构件的延性减少裂缝的产生，增强其抗震性能[14]。研究表明，型钢混凝土能够充分发挥型钢的抗拉性能。为此，本文以剪跨比，轴拉比，偏心距为主要设计参数，设计并制作了13根型钢混凝土柱试件，并对其进行抗震试验，研究其破坏特征，滞回性能，刚度特性，延性以及耗能能力，并提出基于损伤的量化评定。

1 试验概况

1.1 试件设计

本次试验共设计并制作13个型钢混凝土受拉试件，所设计的参数有剪跨比、轴拉比及偏心距。型钢采用Q235的I10普通热轧工字型钢；在工字钢的翼缘外侧通长单排布置螺杆直径为10 mm、长度16 mm的栓钉，其间距为100 mm；通过拉力的中心点与杆件截面的重心点间距离来判定试件是否偏心,试件详细设计参数如表1所示。

表1 试件设计参数Tab.1 Design parameters of specimens

试件具体尺寸及详细配筋图如图1所示。型钢以及钢骨架均焊接在底部250 mm×400 mm×20 mm钢板上，型钢顶部与加载端板焊接。

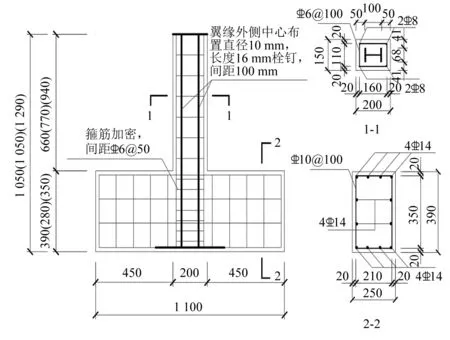
图1 试件几何尺寸及配筋示意Fig.1 Geometry size and reinforcing bars of specimens

试件均采用C40混凝土浇筑，并一同浇筑3组(9个)150 mm×150 mm×150 mm的混凝土立方体试块及1组(3个)150 mm×150 mm×300 mm混凝土棱柱体试块，在常温下实测所得混凝土立方体抗压强度fcu为41.7 MPa，棱柱体抗压强度fc为28.4 MPa，混凝土受力性能指标如表2所示。实测所得钢筋实际弹性模量、屈服强度、极限强度以及伸长率，见表3。

表2 混凝土受力性能指标Tab.2 Mechanical properties of concrete

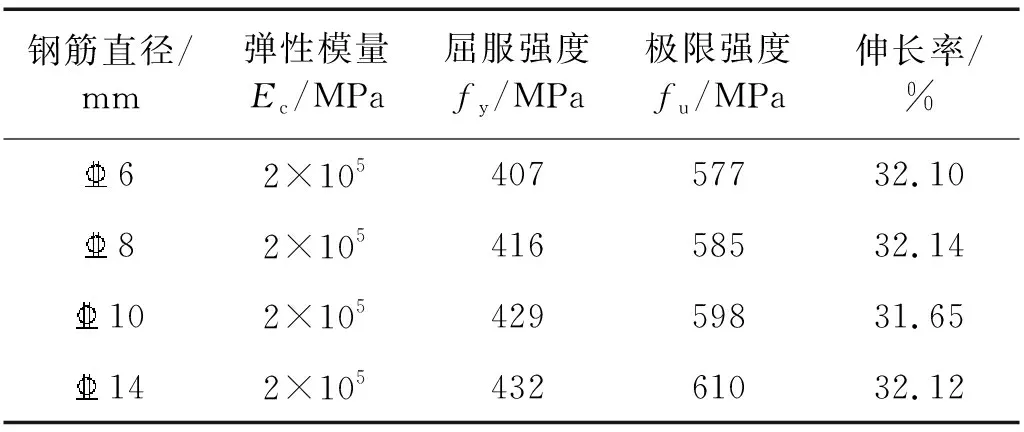
表3 钢材受力性能指标Tab.3 Mechanical properties of steel

1.2 加载方案及测点布置

目前国内外对于轴向拉力低周反复弯剪加载装置比较少见，且并没有统一的标准，本次试验结合实验室条件，并参考文献[15-16]设计了试验装置，制作了加载系统如图2所示。竖向MTS底部加载端板一端用4根高强螺栓与竖向MTS底部连接，另一端与轴心或偏心试件的钢骨顶部加载端板用一根高强螺栓进行连接，如图2所示，形成铰支座以此来实现竖向拉力的施加，轴心、偏心试件顶部加载端板尺寸以及竖向MTS底部加载端板尺寸，如图3、图4所示。水平MTS作动器通过4根高强螺栓与两块钢板与试件相连，并确保水平加载端中心与作动器力臂中心对齐，以此实现水平反复荷载的施加。由于在施加低周反复荷载时，竖向力会存在一定转角，因此在MTS编入程序使竖向力产生转角时其分力能保持不变，以此来控制轴拉比以及偏心距的不变。

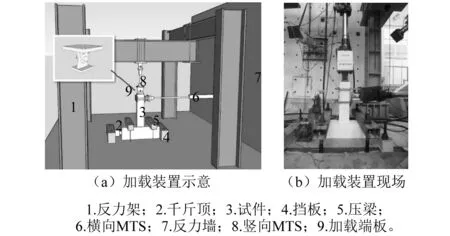
图2 试验加载装置Fig.2 Test set-up

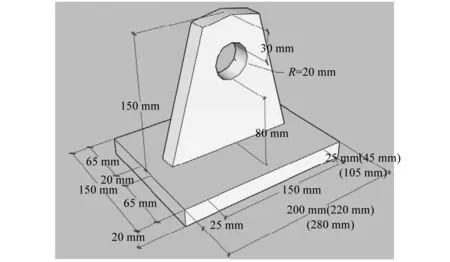
图3 型钢顶部加载端板Fig.3 The top loading plate of steel

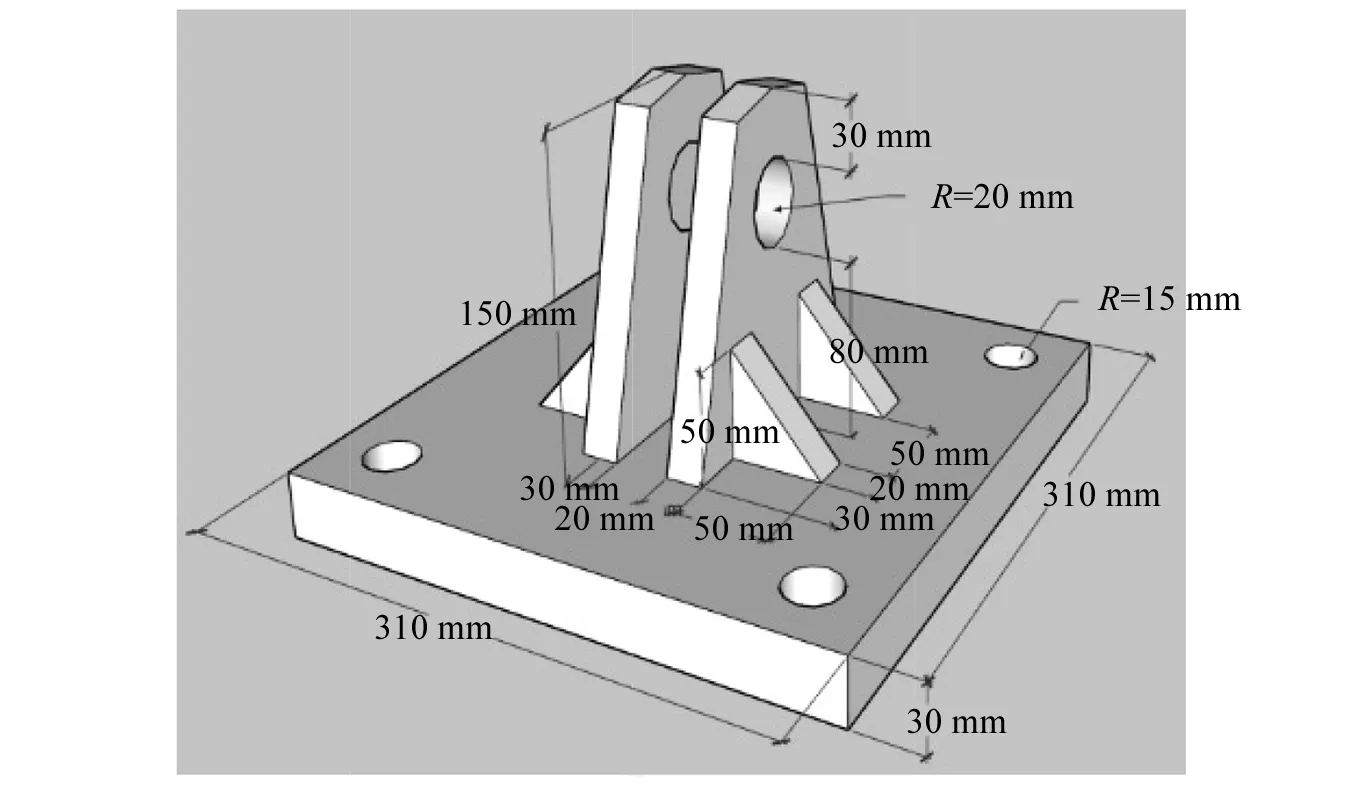
图4 竖向MTS底部加载端板Fig.4 The bottom loading plate of MTS

试验时先在柱顶用竖向作动器施加竖向荷载至指定值，再通过水平作动器施加水平反复荷载。初始以荷载控制，5 kN为一级进行加载，每级循环一次，在试件出现裂缝之后采用10 kN为一级进行反复加载。试件屈服后，改为位移控制进行加载，以屈服位移大小为级差进行加载，并在相同位移下反复循环三次，直到构件水平承载力下降到最大承载力的85%为止。图5为低周反复加载制度示意图，位移计布置以及应变片布置如图6、图7所示。

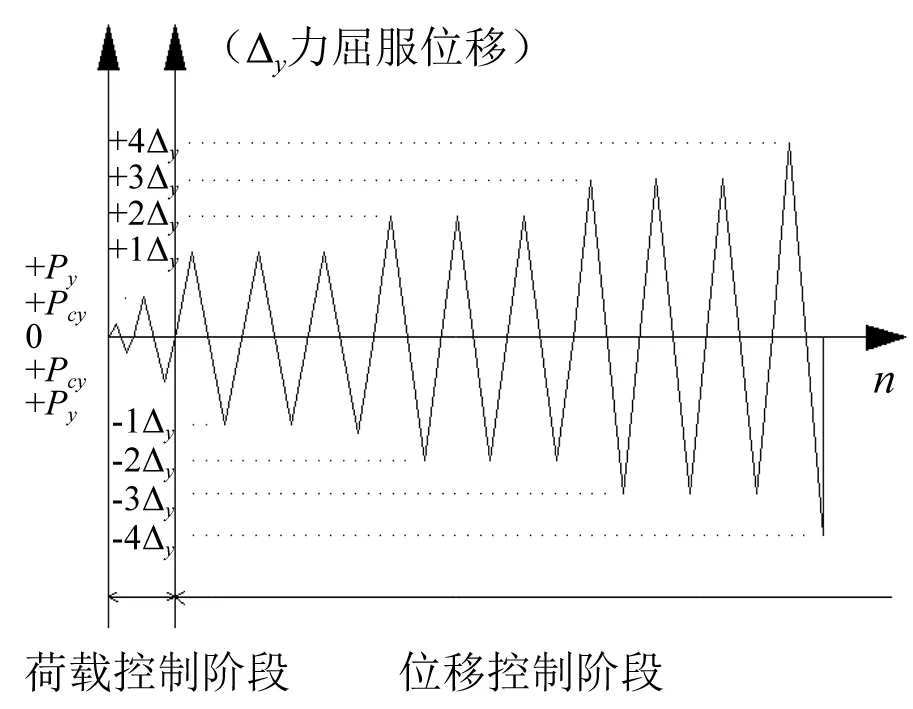
图5 荷载和位移加载控制示意图Fig.5 Loading procedure of test

图6 位移计布置Fig.6 Displacement meter layout

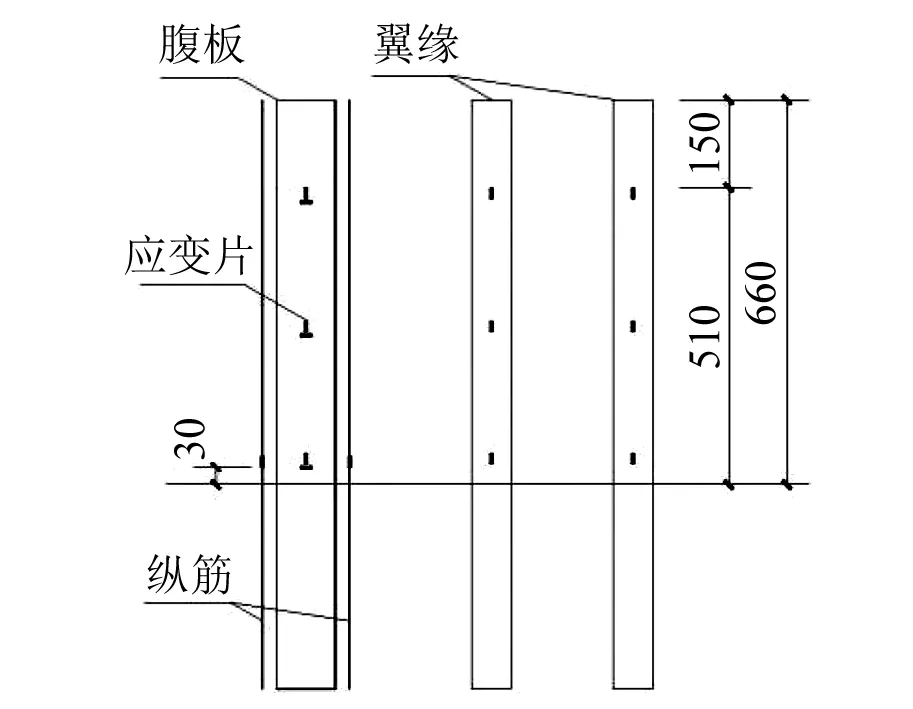
图7 应变片布置Fig.7 Strain gauge layout

1.3 试验数据修正

在低周反复荷载过程中，试件顶端产生水平位移，试件轴线与竖直方向存在转角，竖向拉力作用方向与竖直方向也存在偏角，因此试件上的轴向拉力和水平力需要通过修正后得到[17]。如图8所示，试件受力后试件轴线与力轴线之间的几何关系得

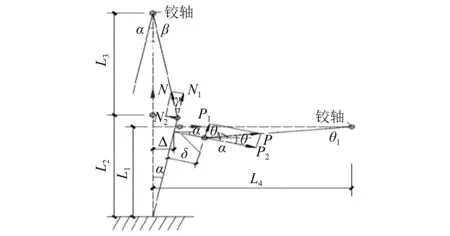
图8 构件变形下受力示意图Fig.8 Force schematic of specimens under deformation

sinα=Δ/L1

(1)

sinβ=ΔL2/L1L3

(2)

(3)

θ=α+θ1

(4)

因此，根据不同加载阶段得出试件实际受力情况

N=N1+P1

(5)

M=P2L2-P1δ-N2L2

(6)

(7)

式中：α为轴线与竖直方向的转角；β为竖向拉力作用方向与竖直方向的偏角；L1为水平力作用点到试件底部距离；L2为竖向力作用点到试件底部距离；L3为竖向力作用点到竖向铰轴的距离；L4为试件轴线到水平铰轴的距离；Δ为水平力作用点处的水平位移；δ为水平力作用点到试件轴线的距离；θ1为水平铰轴与水平面的偏角；θ为α与θ1之和；N为实际竖向拉力；N1为竖向拉力延试件方向的分力；N2为竖向拉力垂直于试件方向的分力；M为试件顶端实际所受弯矩；P为实际水平拉力；P1为水平力垂直于试件方向的分力；P2为水平力延试件方向的分力。

试验结果分析主要通过：轴拉试件分析，偏拉试件分析以及轴拉试件与偏拉试件相对比进行分析。

2 试验结果及分析

2.1 试验过程及破坏

拉弯剪复合作用型钢混凝土柱破坏形态大致分为三类：弯曲破坏、拉弯破坏、弯剪破坏，如图9所示。

图9 试件破坏形态Fig.9 Failure patterns of specimens

弯曲破坏：当试件n=0,e=0 mm时发生弯曲破坏。以试件SCRTM1为例，当荷载达到0.22Pm(Pm为峰值荷载)时，试件根部250 mm范围内出现多条水平裂缝；随着荷载增大，水平裂缝增多，少量水平裂缝受型钢翼缘约束的影响，向腹部斜向延伸；当荷载到达0.83Pm时，试件屈服，水平裂缝较斜裂缝发展迅速，柱下侧角部混凝土被压碎；Pm之后，试件承载力缓慢下降，最终以混凝土大面积剥落，柱根部纵筋外露产生屈曲而试验结束。

拉弯破坏：当试件n≥0.2,e=0 mm时发生拉弯破坏。以试件SCRTM4为例，当荷载达到0.24Pm时，试件上部，中部，底部均有水平裂缝产生；随着荷载逐渐增大，试件各部位水平裂缝增多且大致呈等距分布，底部少量横向裂缝斜向发展；当荷载到达0.67Pm时，试件屈服，水平裂缝不断发展，柱根部水平裂缝宽度发展迅速；Pm之后，混凝土不断剥落，柱根部与地基梁受拉而脱离，试件结束。

弯剪破坏：当试件n=0.2,e≥20 mm时，试件发生弯剪破坏。以试件SCRTM12为例，当荷载达到0.19Pm时，试件根部出现斜裂缝及少量水平裂缝；随着荷载增大，试件斜裂缝增多，腹部斜裂缝交叉形成交叉斜裂缝，且原有水平裂缝逐渐向腹部斜向发展；当荷载达到0.83Pm时，试件屈服，斜裂缝较水平裂缝发展迅速；Pm之后，偏拉侧混凝土局部剥落，钢筋屈服，荷载下降到85%Pm时试件破坏。

通过试验现象，试验可概括为3个阶段：①未裂阶段，试件处于弹性阶段，混凝土、钢筋以及型钢共同承担外力；②带裂缝工作阶段，受拉区混凝土逐渐退出工作，试件外力由钢筋与型钢共同承担，试件内部剪应力发生重分布，混凝土承担的剪力将逐渐传递给型钢以及箍筋；③破坏阶段，未屈服的箍筋以及型钢翼缘对核心区混凝土还存在一定约束作用，试件水平荷载仍可增大，混凝土裂缝宽度与长度迅速增加，峰值荷载后，水平荷载逐渐下降，试件破坏。

2.2 滞回曲线

图10为各试件在低周反复荷载作用下水平荷载P与柱顶位移Δ的滞回曲线，对比各曲线可得：

如图10(a)、图10(b)所示，对于轴拉试件，随着轴拉比从0增大到0.6，滞回曲线饱满程度呈下降态势，试件极限位移逐渐减小，后期荷载下降速率增大，表明耗能性能逐渐降低。如图10中SCRTM2，SCRTM4以及SCRTM13所示，随着剪跨比从1.80增大到3.20，滞回曲线饱满程度增大，水平荷载下降减缓，抗震性能增强。

如图10(d)、图10(e)所示，对于偏拉试件，随着偏心距的增大，滞回曲线饱满度降低，极限变形也随之减小，延性及耗能能力逐渐降低，表明抗震性能逐渐减弱。

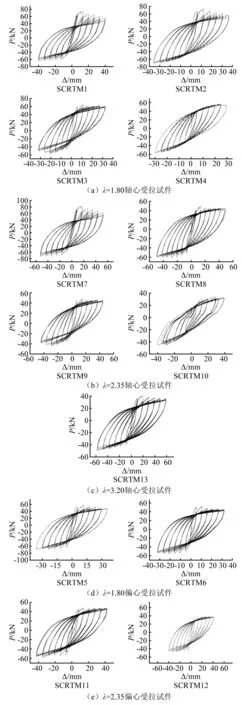
图10 试件滞回特性曲线Fig.10 Component hysteretic characteristic

轴拉试件与偏拉试件相比，相同点：各试件滞回曲线大致均呈梭形形状，表明其具有良好的抗震性能。不同点：偏拉试件曲线饱满程度较低，极限位移较小，刚度退化趋势较快，主要是由于试件偏拉侧在反复荷载作用下损伤较大导致。

2.3 骨架曲线、承载力及延性

试件骨架曲线如图9所示，各特征点的承载力与位移以及试件延性系数汇总如表4、表5所示。

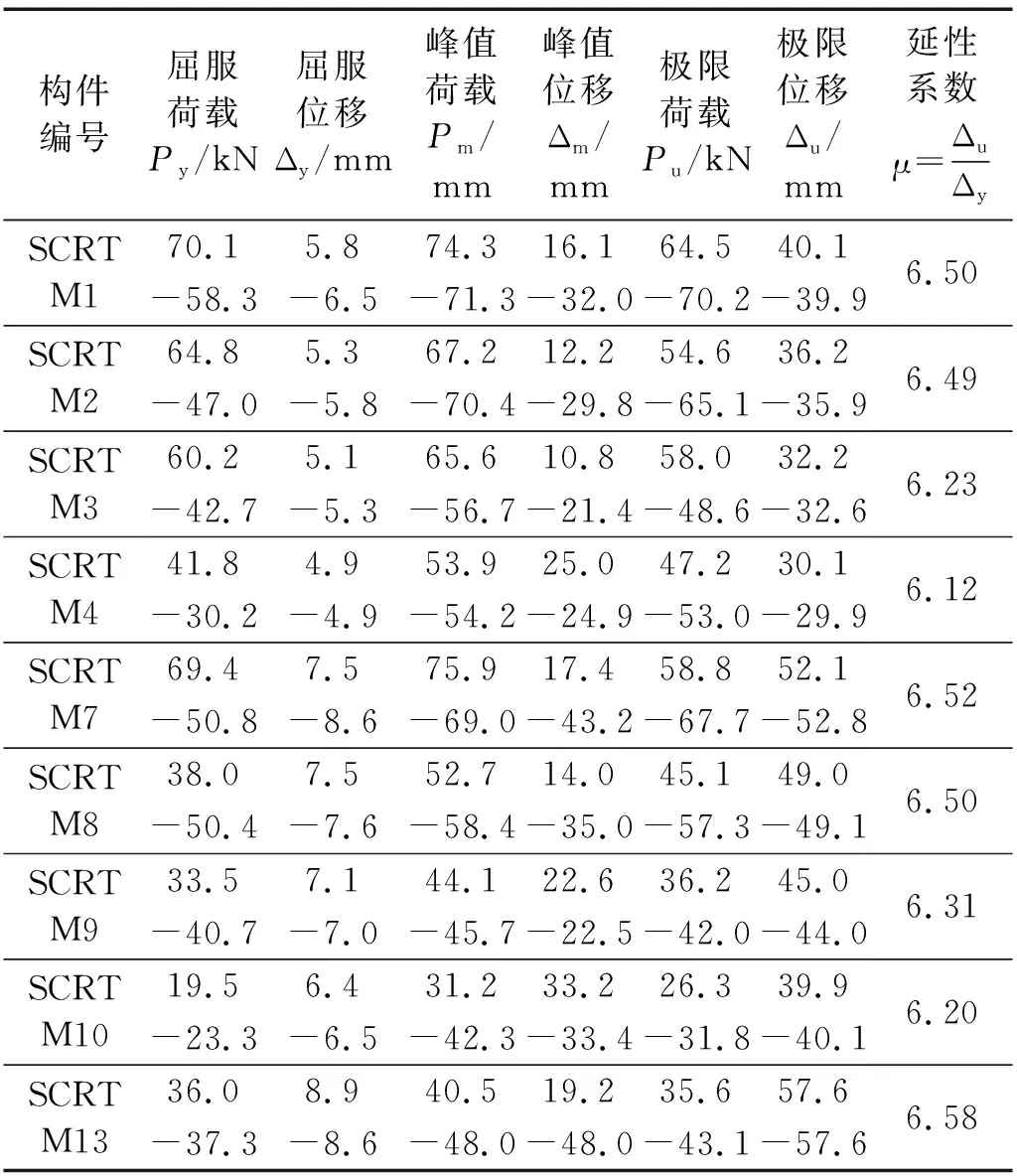
表4 轴拉试件试验结果Tab.4 Shaft pull specimens experimental results

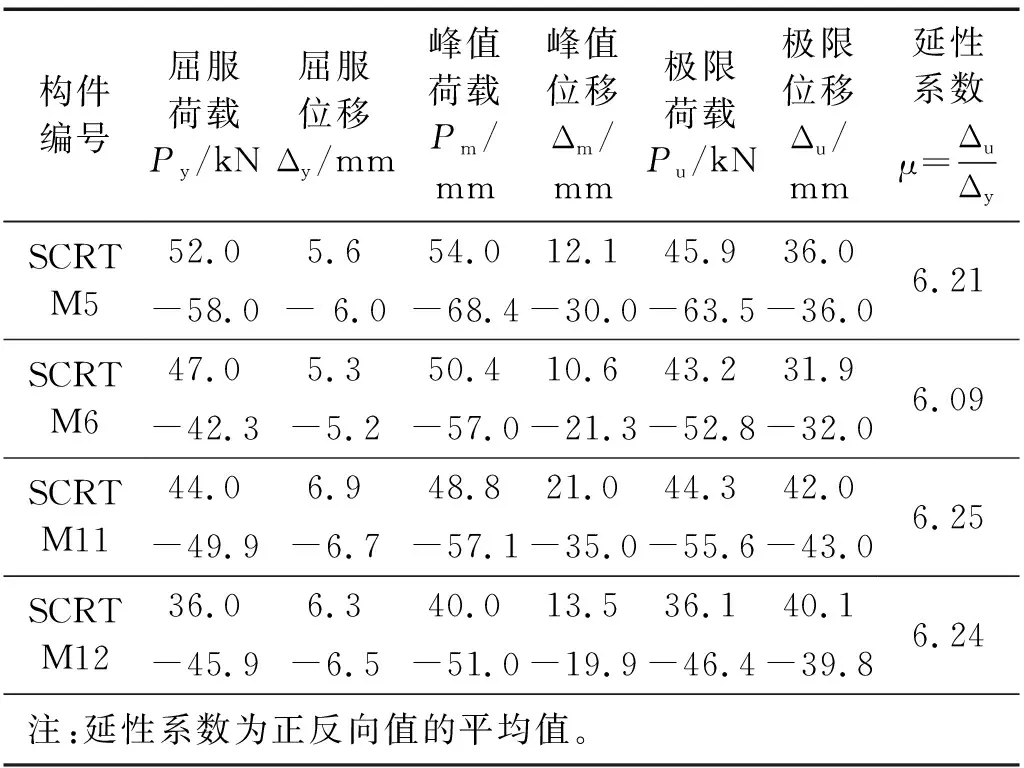
表5 偏拉试件试验结果Tab.5 Partial pull specimens experimental results

如图11(a)、图11(b)所示, 对于轴拉试件，随着轴拉比的增大，峰值荷载逐渐减小，降低幅度在5.49%～49.28%，刚度退化加快，试件延性能力降低，最大降低幅度为5.84%。如图11(c)所示,随着剪跨比的增加，峰值荷载逐渐减小，曲线下降段越平缓，延性及耗能能力增强，试件SCRTM13与试件SCRTM2相比峰值荷载降低35.68 %，延性系数增大1.39%。

如图11(d)、图11(e)所示,对于偏拉试件，随着偏心距的增加，峰值荷载以及延性系数均呈下降态势，试件SCRTM6与试件SCRTM5相比峰值荷载降低12.25%，试件SCRTM12与试件SCRTM11相比峰值荷载降低14.07%。

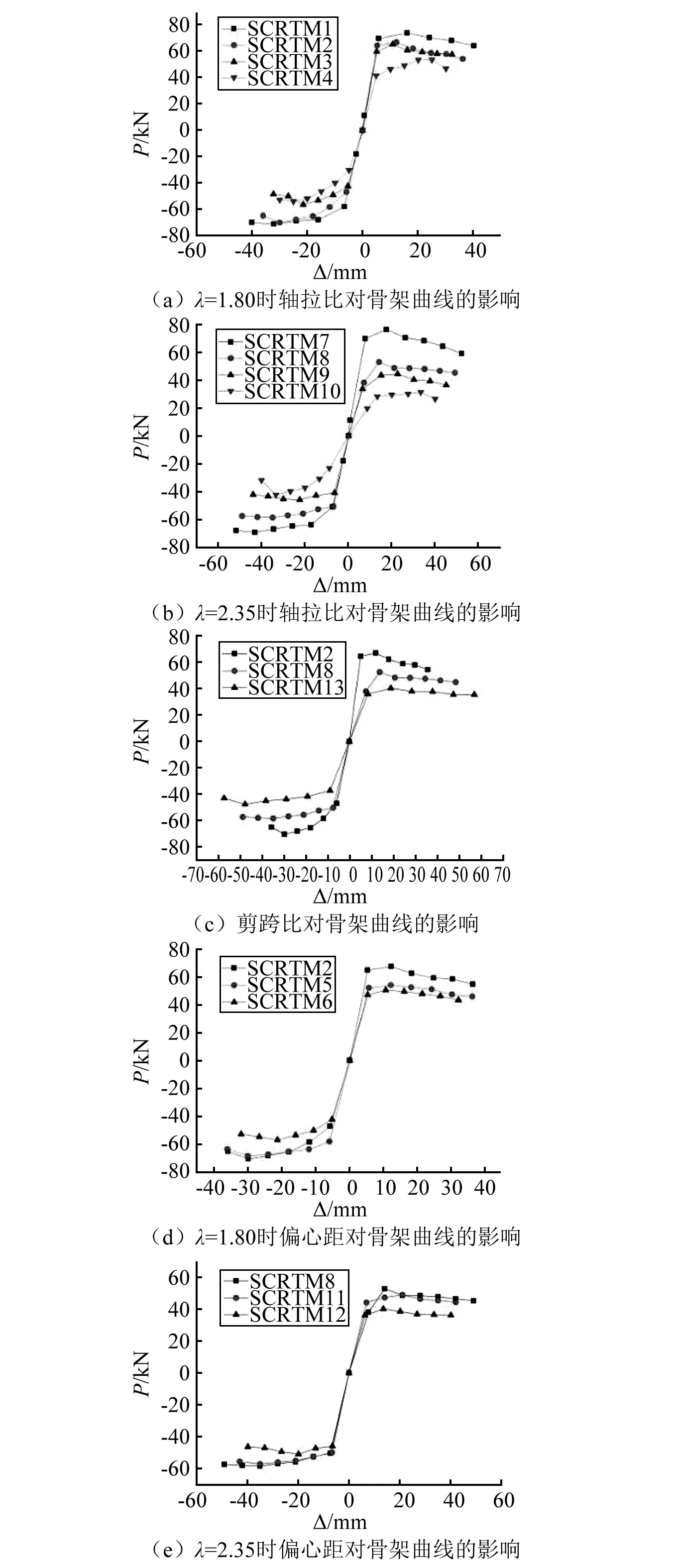
图11 试件的骨架曲线Fig.11 Skeleton curves of specimens

轴拉试件与偏拉试件相比，相同点：试件延性系数均大于6，表明试件屈服后承受变形的能力较强，在其完全破坏之前，型钢的塑性得到充分发展。不同点：轴拉试件比偏拉试件峰值荷载高18.09%～21.95%，延性系数大3.85%～6.16%。

导致两类试件骨架曲线、承载力以及延性有所不同的原因为：偏心受拉试件由于偏心距的存在，导致试件受拉侧与受压侧差别较大，受拉侧比受压侧承载力相对较弱，下降态势快，延性变形能力相对较低。

2.4 耗能能力

本文采用等效粘滞阻尼系数he来表征试件的耗能能力，可按式(8)计算得到

(8)

式中：SABCD为试件加载滞回环面积；SBOE+DOF为试件加载滞回环上下顶点相对应的三角形面积之和，如图12所示，试件等效黏滞阻尼系数如表6所示。

表6 试件等效黏滞阻尼系数Tab.6 Equivalent viscous damping coefficients of specimens

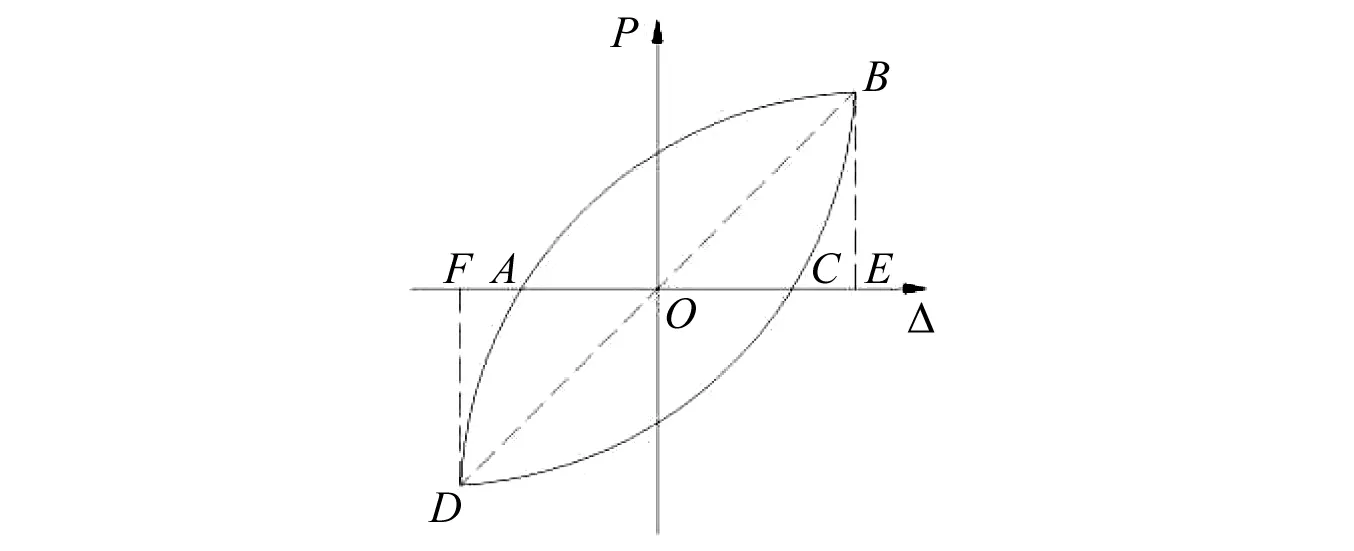
图12 滞回曲线示意图Fig.12 Schematic diagram of hysteresis curve

对于轴拉试件，随着轴拉比的增大，试件等效阻尼系数均降低，表明试件耗能能力逐渐减弱。随剪跨比的增大，试件等效黏滞阻尼系数逐渐增大，试件SCRTM13比SCRTM2破坏点等效黏滞阻尼系数增大14.47%。

对于偏拉试件，随着偏心距的增加，等效粘滞阻尼系数逐渐降低，降低幅度在3.41%～3.52%。

轴拉试件与偏拉试件相对比，相同点：等效阻尼系数均大于0.1，表明试件具有良好的耗能能力。不同点：试件SCRTM6与SCRTM2相比破坏点等效阻尼系数降低28.93%，试件SCRTM12与SCRTM8相比破坏点等效阻尼系数降低14.91%，因此可得，轴拉试件比偏拉试件耗能能力强，但随剪跨比的增大，等效阻尼系数下降趋势逐渐减缓。

导致两类试件耗能能力有所不同的原因为：偏心距的增大导致试件滞回环饱满程度呈下降态势，包含面积逐渐减小。

2.5 刚度退化

试件刚度退化采用式(9)进行计算，图13给出了各试件刚度退化趋势

(9)

式中：Ki为割线刚度；Fi为第i次峰值点的荷载；Xi为第i次峰值点荷载对应的位移。

如图13(a)所示，对于轴拉试件，随着轴拉比的增大，刚度退化趋势逐渐加快。主要由于轴拉比越大，在循环加载时试件裂缝越多所产生的损伤累积增大，致使试件刚度退化速率加快。随着剪跨比的增大，试件初始刚度逐渐减小，且刚度退化速率变缓慢，表现出较好的抵抗循环荷载作用的能力。

如图13(b)所示，对于偏拉试件，随偏心距的增大，初始刚度逐渐减小且刚度退化曲线逐渐陡峭，刚度退化速率逐渐增大。

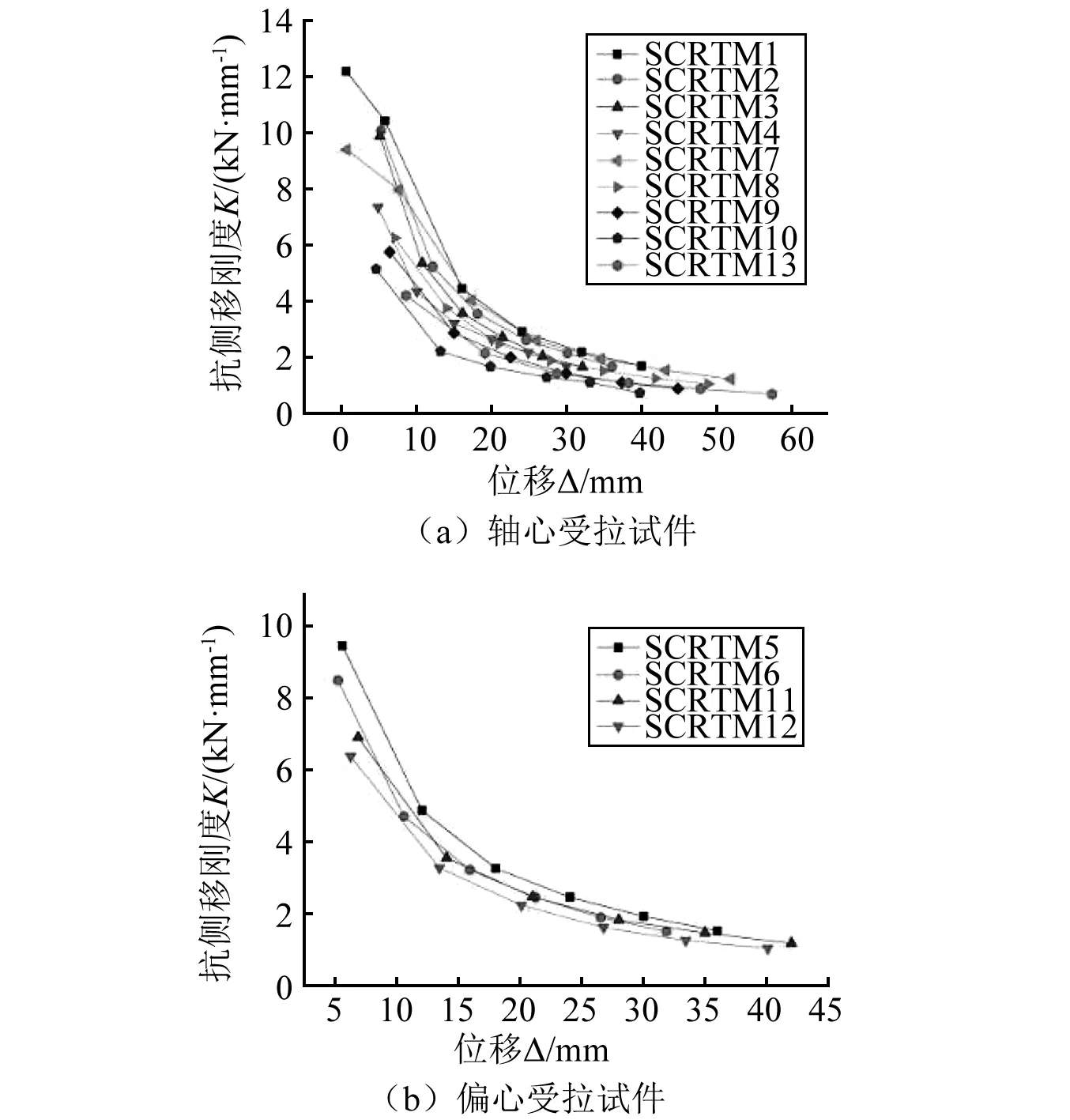
图13 试件刚度退化曲线Fig.13 Stiffness degradation of specimens

轴拉试件与偏拉试件相比，相同点：各试件的刚度退化曲线均较为平缓，表明试件在循坏荷载作用后期仍具有一定的刚度，损伤发展较平稳。不同点：轴拉试件刚度退化曲线较为平缓，退化速率较慢，而偏拉试件刚度退化速率较快，偏心距越大，这种趋势越加明显。

导致两类试件刚度退化速率有所不同的原因为：反复荷载作用下偏拉试件累积损伤较大且偏拉侧刚度退化速率较快。

3 损伤量化分析

结构在低周反复荷载下产生的损伤一般采用损伤指数D反映其损伤程度。基于能量守恒定律, 把试件当作为一个独立的系统, 当系统所处状态产生变化时, 系统所产生的内能增量等于变化过程中外界对其所做的功以及吸收热量之和。

如图14所示，在理想无损伤情况下，第i次循环试件所作的功Wi为SOAB与SO′A′B′面积之合，加载路径正向按直线OAB进行，负向按直线OA′B′进行，为

(10)

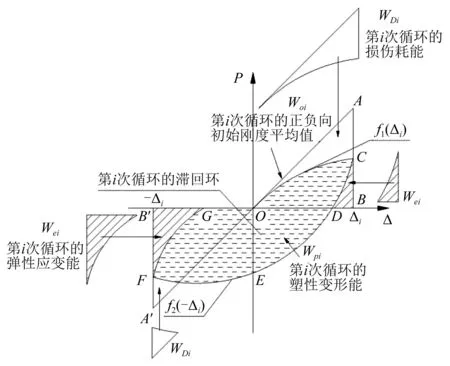
图14 某级循环能量耗散示意图Fig.14 Cumulative energy consumption of hysteretic loop under a circle

式中：Wi为第i次循环下理想无损伤时外力所做功；K0i为第i次循环下试件正反向初始加载刚度平均值；Δii为第i次循环下试件的最大位移。

非理想状态下，第i次循环加载路径应按曲线OCDEFG进行，荷载卸为零后，产生了残余变形，累积损伤因此而产生。此循环下外力所做的功可分为三部分：Wei为第i次循环的弹性变形能，即SBCD与SB′FG面积之合；Wpi为第i次循环的塑形变形能，即面积SOCDEFG，表示的含义为系统吸收与耗散的能量；WDi为第i次循环的损伤耗散能，即外力所作的功为

Wi=Wei+Wpi+WDi

(11)

其中，

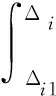
(12)

式中：Δi1为第i-1次循环反向卸载为零时的残余变形;Δi2为第i次循环正向卸载为零时的残余变形；f1(Δi)为第i次循环正向加载函数；f2(-Δi)为第i次循环反向加载函数。

即损伤指标D表示为

(13)

如表7、表8所示，在拉弯剪复合作用下型钢混凝土柱破坏时损伤指数处于0.804～0.963。

如表7所示，对于剪跨比为1.80与2.35的轴拉试件，破坏时损伤指数随轴拉比的增大而增大，增大幅度在1.33%～14.37%。其主要是由于轴拉力的增大，试件裂缝分布逐渐增多且开展越充分，试件内部损伤程度增大。随剪跨比的增大，试件的损伤指标逐渐降低，试件SCRTM13与试件SCRTM2相比破坏时损伤指数减小了11.55%。

如表8所示，对于偏拉试件，随偏心距的增加，试件损伤指标逐渐增大。主要由于偏心距的影响，试件受拉侧更加容易产生损伤。试件SCRTM6与试件SCRTM5相比破坏时损伤指数增大了0.42%，试件SCRTM12与试件SCRTM11相比破坏时损伤指数增大了5.17%。

轴拉试件与偏拉试件相比较，相同点：在试件开裂时损伤指数相差不大，试件开裂后损伤指数增长加快。不同点：试件SCRTM6与试件SCRTM2相比破坏时损伤指数增大了4.62%， SCRTM12与试件SCRTM8相比破坏时损伤指数增大了11.44%。由此可得，偏拉试件更易产生损伤。

根据表7、表8试件主要阶段累积损伤指数值提出了表9拉弯剪复合作用下型钢混凝土柱不同破坏阶段的损伤量化值，可供该类试件的性能评定以及修复提供参考。

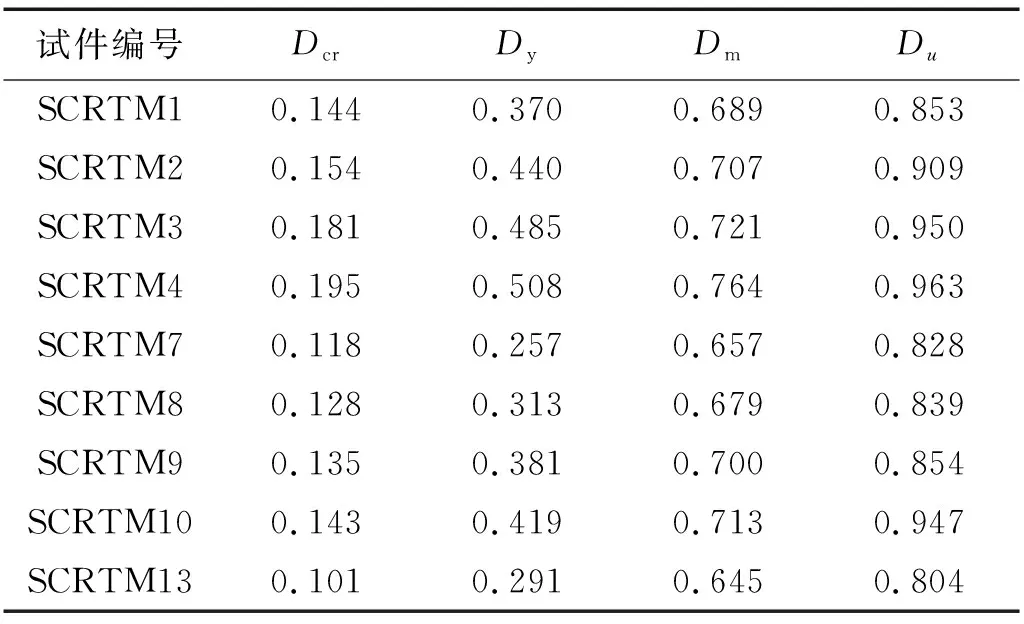
表7 轴拉试件各主要阶段累积损伤指数Tab.7 Result of cumulated damage index of shaft pull specimens in main stage

表8 轴拉试件各主要阶段累积损伤指数Tab.8 Result of cumulated damage index of partial pull specimens in main stage

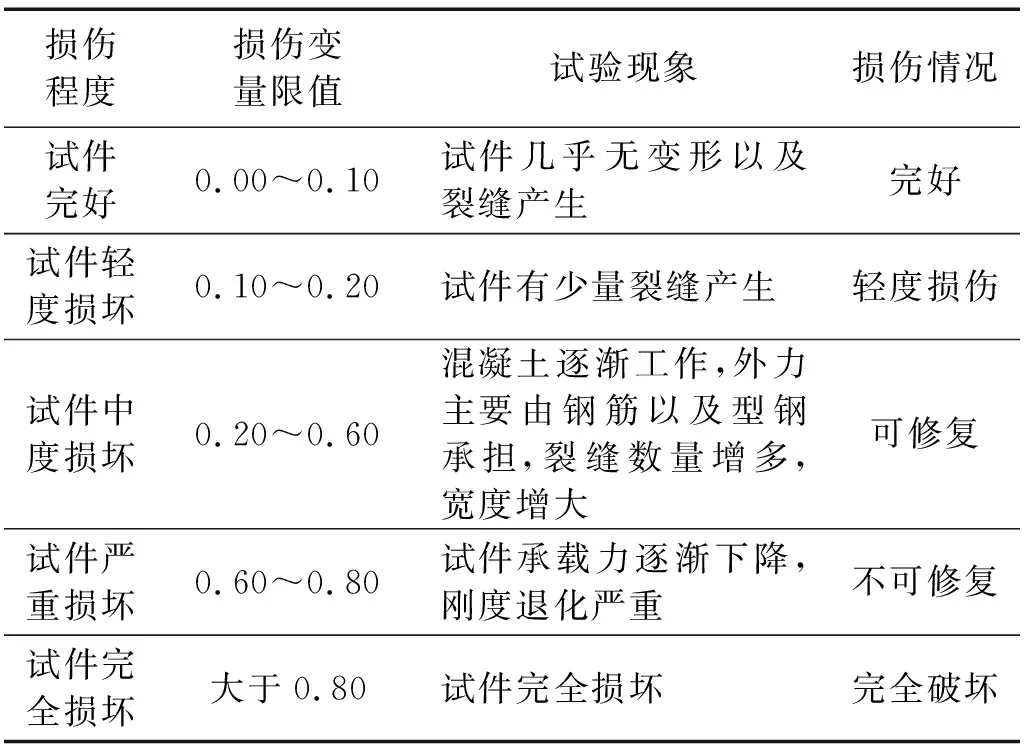
表9 拉弯剪复合作用下型钢混凝土柱的损伤量化Tab.9 Damage quantization of steel reinforced concrete columns subjected to constant tension and cycled flexure-shear

4 结 论

通过13个不同的轴拉比、剪跨比、偏心距的型钢混凝土柱在拉弯剪复合作用下的抗震试验可得到以下几点结论:

(1)拉弯剪复合作用下型钢混凝土柱在轴拉比、剪跨比、偏心距不同的影响下，破坏形态主要有受弯破坏、拉弯破坏以及弯剪破坏。

(2)拉弯剪复合作用下型钢混凝土柱试件位移延性系数均超过6，表明试件的变形能力较大。

(3)所有试件处于弹性阶段时损伤指标接近于0，随着荷载的增大，损伤指标不断增大，破坏时试件的损伤指标介于0.804～0.963。

(4)轴拉试件滞回曲线饱满，最大承载力以及位移延性较好，抗震性能良好。随轴拉比的增大，滞回曲线饱满度呈下降态势，延性变形能力、水平承载能力以及损伤指标逐渐降低，抗震性能逐渐减弱。随剪跨比的增大，滞回曲线饱满度以及位移延性增加，但最大承载力以及损伤指标逐渐下降。

(5)偏拉试件随偏心距的增大，滞回曲线饱满度呈下降态势，最大承载力及位移延性逐渐下降，刚度退化加快，损伤指标不断增加，抗震性能逐渐减弱。

(6)轴拉试件与偏拉试件相对比，轴拉试件滞回曲线更加饱满，承载力以及位移延性相对较高，耗能能力较强，刚度退化较为缓慢，损伤指标相对较小，因此，抗震性能要优于偏拉试件。