基于流固耦合的重载飞艇副气囊形态分析与试验研究

艾科热木江·塞米， 袁行飞， 陈务军， 王雪明， 张大旭

(1. 浙江大学 空间结构研究中心，杭州 310058；2. 上海交通大学 空间结构研究中心，上海 200240； 3. 中航工业特种飞行器研究所，湖北 荆门 448035)

飞艇是一种依靠气囊中浮力工质气体提供静浮力，依靠发动机和螺旋桨提供推力的飞行器。软式飞艇由直接作为外蒙皮的主气囊，以及产生内外压差来保持艇体外形的副气囊组成。重载飞艇和平流层飞艇内置气囊采用的浮升气为氦气[1]。氦气囊在不同高度、巡航阶段呈现不同的充盈度和形态，氦气囊充盈度将决定浮力的大小、浮心位置变化，进而影响飞艇姿态控制[2-3]，目前主要是基于经验考虑，尚难定量分析，但是针对新型重载飞艇或大型平流层飞艇，建立有效数值模拟方法尤为必要。针对氦气囊或者囊体非稳定形态的研究较少，文献[4]结合Abaqus软件和FLUENT软件，对飞艇外气囊与周围空气流场进行流固耦合分析。文献[5]研究飞艇主气囊的模态特性及试验验证模态分析方法。文献[6]针对飞艇非保形升空时囊体非保形的形态进行模拟分析。文献[7]以正高斯曲率氦气囊为对象，采用CFX软件分析不同仰角下的非饱和形态。重载飞艇内置氦气囊构型复杂，升空和循环过程形态变化和力学行为复杂，包括大变形、褶皱、接触干涉等非线性，以及内部氦气和外部空气及与囊体耦合作用，然而相关理论与数值分析鲜有报道。

流固耦合[8]问题最初在航空航天领域被提出之后，多种分析理论和计算方法在交叉学科领域中取得了快速发展。文献[9]提出了基于交错积分的弱耦合方法，文献[10]进一步研究了基于同步迭代的弱耦合方法，这些方法将固体域和流体域控制方程分开求解后进行CSD(computational structural dynamics)/CFD(computational fluid dynamics)之间数据传递。文献[11]研究了在同一控制方程中求解所有变量的强耦合方法。然而此方法对复杂边界的适应性低，计算工作量大等原因，大部分主流的CFD分析软件采用基于弱耦合理论的双向流固耦合分析方法。

向量式有限元(vector form of intrinsic finite element，VFIFE)[12-14]是基于向量式固体力学和有限元的数值计算方法。在研究几何、材料、边界非线性以及结构静动力问题比传统有限元法具有优越性。基于有限元法的计算流体力学计算方法对气囊形态变化中可能出现的任意几何形状的适应性很好，对复杂边界流域可以实现高阶离散精度，因此非常适用气囊的形态分析问题。

本文将向量式有限元擅长解决强非线性问题以及流体力学有限元法适用于任意几何边界条件的特点结合起来，采用双向流固耦合理论分析飞艇内置氦气囊的不稳定形态变化。同时开展缩尺比例模型试验，与数值分析结果加以对比，验证了本文提出的分析方法的适用性和准确性。

1 向量式有限元

氦气囊是由聚酰胺纤维薄膜制作而成，本文采用常应变三角形膜单元进行气囊建模。以下简单介绍向量式有限元膜单元基本理论[15]。

1.1 质点运动方程

向量式有限元首先将结构分解为一组离散的空间点组成的质点群，相邻质点之间的参数用一组标准化的内插函数表示，从而避免了有限单元法用微分形式的连续函数描述结构。其次，用一组时间点组成的控制方程描述空间点的运动过程。控制方程中的质点间相互作用力仅与相对位置中的纯变形有关，因此使结构作虚拟逆向运动，从总位移中扣除刚体运动分量得到纯变形，进而求解单元内力，得到结构的内力分布。质点运动的控制方程为牛顿第二定律方程式，即

(1)

竖向压力按气囊内外气体的密度差随高度呈线性分布，同一高度气体环向压力近似认为处处相等，如图1所示。气囊在不稳定形态变化中，某一高度下的内外压强相等，称之为零压面。由于氦气密度比空气小，气囊在零压面以上处于膨胀(超压)状态，而零压面以下则处于收缩(负压)状态。考虑到几何形状、流场变化以及外界因素等将对实际压力梯度产生较大的影响，因此模拟分析中先按假设的压力梯度求出节点位移后接着通过流体力学计算获得真实压力分布，并修正节点外力矩阵。

图1 压力梯度示意图Fig.1 Schematic diagram of pressure gradient

1.2 边界非线性

气囊在泄气过程中将产生褶皱和碰撞接触等复杂力学行为，因此单位时间内需检测接触单元并对其进行碰撞响应处理。碰撞检测是整个边界非线性问题中最耗时的工作，本文首先对整体空间域进行较粗略的全局检测，然后对各个子空间域进行精确的局部检测。全局检测是把整个囊体所在空间域划分成若干大小相等的子域之后，确定所有节点和单元所属子域，单元可按形心点坐标划分所属子域。然后存储每个子域所包含的节点和单元编号。由于向量式有限元时间步长非常小，假设单元只可能与所在子域及周围3×3×3子域内的节点发生碰撞，从而大大减小了搜索计算量。局部检测是前后两个时刻的节点位于单元两侧，以及穿透点位于单元内部时可认为发生碰撞，此时两个三角形的接触可转化为点-三角形接触问题。

确定发生碰撞的节点和单元之后，计算虚拟接触力进行碰撞响应处理。本文采用罚函数法[16]计算法向排斥力和切向摩擦力，然后将该力反向施加到发生碰撞的节点和单元，修正节点力矩阵并重新求解质点运动方程。

2 流体力学有限元法

流体力学有限元法的基本思想是将流体域划分成有限个离散的子区域，对于各子域按照一定规则构造基函数，对整个单元区域进行积分得出单元有限元方程，从而使用各子域差分方程的近似解逼近微分方程的精确解[17]。

2.1 离散方程

流体力学基本方程主要包括连续方程、动量方程、能量方程等，按研究对象的复杂程度可以考虑理想气体状态方程、组分方程和湍流方程使总控制方程闭合。使用φ表示通用变量，则离散化的单元矩阵[18]可表示为

[Te+Ae+De]{φe}={Se}

(2)

式中：T为瞬态项；A为对流项；D为扩散项；S为源项。将单元权函数We代入式(2)中的各项，在单元内积分表达式为

(3)

(4)

(5)

(6)

式中：ρ,Ω,Γ,v分别为单元密度、体积、扩散系数和速度；矢量符号div为散度； grad为梯度。

2.2 CFD求解

ANSYS Flotran是Mechanical APDL内部基于有限元法的流体力学计算模块。与Fluent，CFX等主流流体计算软件相比，Flotran具有以下特点：

(1) Flotran采用有限元法，而Fluent，CFX等软件采用有限体积法。在本文流固耦合计算中，需要跟踪单元网格上各节点的速度、压强等变量信息。有限元法中的离散方程定义明确，与向量式有限元结合运用，使流固耦合计算更简便。

(2) Flotran和MATLAB基于Fortran语言开发，而Fluent，CFX等软件基于C语言开发。由于本文中向量式有限元采用自编MATLAB程序，因此与Flotran配合可使编程语言统一化，计算更简便。

另外，Flotran不需要进行人机交互式界面操作，容易实现程序化模块并被其他程序调用，因此本文采用ANSYS Flotran进行CFD求解。

Flotran的CFD求解过程是首先假定一个初始流速分布以求解压力方程，得到速度和压力后代入组分传输方程和湍流方程，然后用求出的湍流动能k和湍流动能耗散率ε更新有效黏度，进入下一步迭代直至各自由度收敛。

3 流固耦合分析

3.1 映射网格

在固体域中单元变形和节点位移远小于流体域中的变化量，因此固体网格比流体网格更稀疏。此时需要插值函数将固体网格和流体网格上的节点力、位移建立映射关系，为CFD/CSD之间的数据交换起桥梁作用。本文采用一种基于薄板样条(thin plate spline，TPS)函数[19]的插值方法。us,uf分别为固体网格和流体网格上的节点位移，则

uf=Hus

(7)

式中，H为插值矩阵。同理，Ps,Pf分别为固体网格和流体网格节点上的荷载，由虚功原理得出

δW=δufPf=δusPs

(8)

将式(7)代入式(8)可得

Ps=HTPf

(9)

3.2 双向流固耦合

基于流固耦合的氦气囊形态分析具体步骤如下：

步骤1将初始模型导入到固体模块，设置材料属性、几何参数、约束条件等；同时将初始模型导入到流体模块，进行前处理、设置边界条件。

步骤2固体模块按照氦气充盈度和囊体体积确定零压面高度，计算压力梯度和初始节点外力矩阵。

步骤3中央差分法计算节点位移，更新节点坐标。若发生接触碰撞，计算接触力并修正节点力矩阵，重新计算节点位移。

步骤4从节点位移依次计算各单元的纯变形、应变、应力和内力，最后反作用于节点上得到节点内力。

步骤5由重力和压力梯度计算节点外力，集成节点力矩阵。

步骤6重复步骤3～步骤5，直至模型趋于平衡，然后将步骤3得到的节点位移通过映射网格传送到流体模块。

步骤7更新流体模块中的节点坐标，依次求解N-S方程、组分传输方程和湍流方程直至各自由度收敛。

步骤8得到的节点压力分布通过映射网格传送到固体模块修正压力梯度，回到步骤5。

步骤9重复步骤6～步骤8，直至该模型趋于稳定。

步骤10改变充盈度，回到步骤2，重新计算气囊形态；如果出现发散即结束程序并调整初始参数。

具体计算流程如图2所示，图中左边区域为固体模块，在自编MATLAB程序中进行；右边区域为流体模块，在ANSYS软件的Flotran模块中进行。

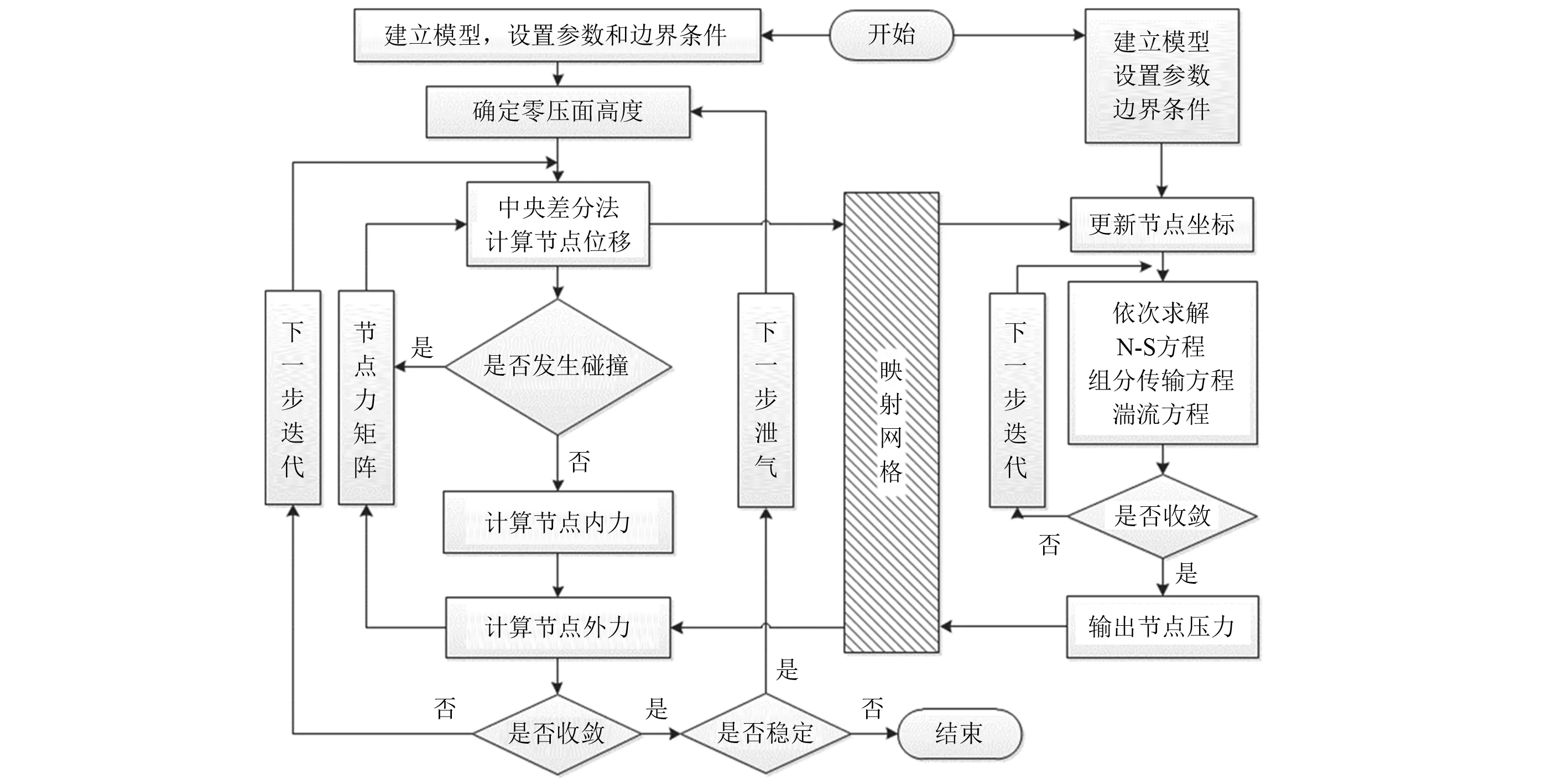
图2 双向流固耦合流程图Fig.2 Flow chart of two-way fluid-solid coupling

4 试验设计与数值分析

为了研究气囊随氦气充盈度变化导致的形态变化规律，本文采用飞艇内置气囊专用聚酰胺纤维材料制作了一20∶1比例仿真模型进行泄气试验，并采用本文建立的双向流固耦合方法进行数值模拟，最后将模型试验和数值模拟结果进行对比。

4.1 试验设计

试验设备主要包括囊体、氦气瓶、导气管、真空泵和固定装置。囊体初始几何模型如图3(a)所示。囊体前、后、侧面均布置用于位移测量的靶点。囊体在泄气过程中，如约束数量不够，会出现一直晃动而影响靶点的位移测量。因此本试验布置了囊体上的18个xyz方向全约束的固定点：顶部区域共三排固定点，每排三个；三角网处共计 9 个固定点沿三角线分布，如图3(b)所示。

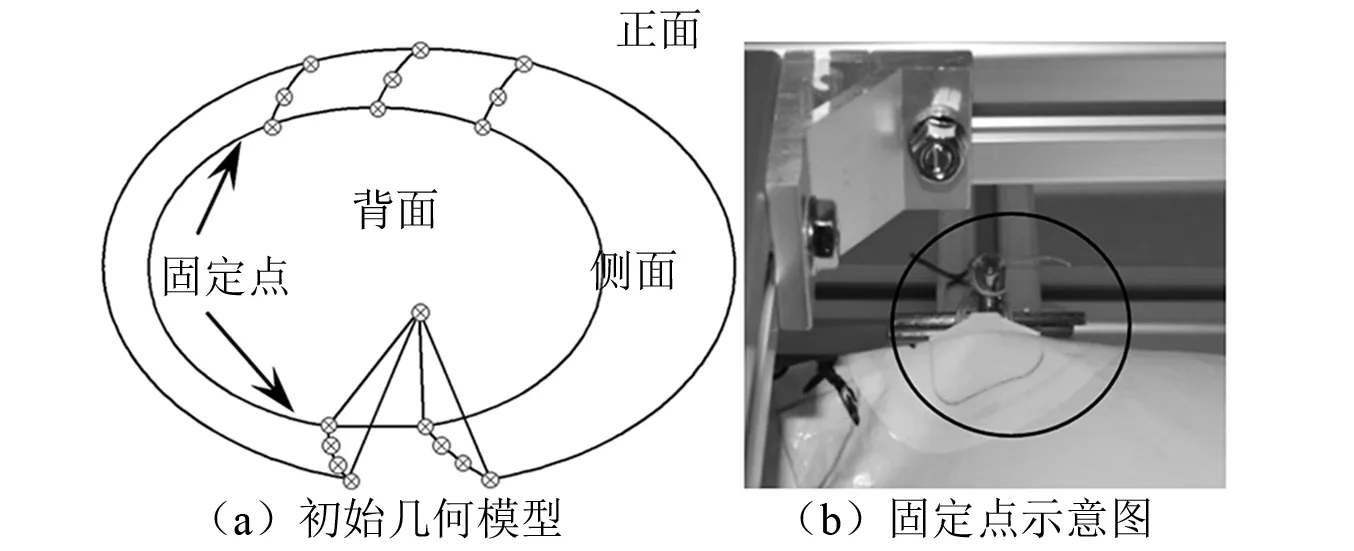
图3 初始几何模型与固定点示意图Fig.3 Schematic diagram of initial geometric model and fixed points

本试验中分别在气囊正面、背面和侧面上选取若干靶点作为控制点：正面-7，8，9；背面-21，23，30；侧面-27。试验模型及控制点布局如图4所示。

图4 试验模型及控制点Fig.4 Test model and control points

采用三台照相机对囊体同一个面上的靶点分别从三个角度进行拍摄，最后通过计算处理得到靶点相对标定面的实际空间位置。依照该方法可以得到囊体表面在不同泄气状态下相对同一标定面(即同一空间直角坐标系)的空间位置。对比初始泄气状态下的空间位置，可以得到不同泄气状态下的靶点的空间位移，从而得到囊体在不同氦气充盈度下的形态位移变化。

本试验中，首先将氦气囊充气至初始几何参考模型的1.25倍，即125%充盈度，然后通过预设的固定点固定住氦气囊进行泄气试验，测量气囊上的控制点在不同氦气充盈度下的位移，得到囊体随着氦气充盈度减小的形态变化规律。

囊体的泄气采用真空泵抽出氦气，由于本试验设计的氦气囊囊体气嘴处于囊体顶部，氦气密度远小于空气，抽气过程中囊体内剩余氦气始终聚集于囊体顶部区域，因此最后囊体内的氦气可以被真空泵抽取完。试验中采用分级泄气控制方案，将氦气囊从125%充盈度状态抽气直到抽干为止，一共分19级泄气，第一次抽气时间为5 min，其余各级抽取时间为3.6 min。泄气试验过程如图5所示。

图5 泄气试验过程Fig.5 Process of deflation experiment

4.2 数值模拟

固体模块采用向量式有限元理论在自编MATLAB程序中计算。每次泄气计算时间0.5 s；时间步长1×10-4s；各充盈度下的循环步数5 000；应力应变输出步数100；碰撞检测步数10；褶皱处理步数1；虚拟阻尼100。气囊的材料参数如表1所示。

表1 气囊膜材料参数Tab.1 Material properties of membrane

流体模块采用流体力学有限元法的ANSYS Flotran求解器中计算。泄气时间和时间步长与固体模块一致。氦气域和空气域均采用Fluid 142单元进行计算。将初始模型划分网格后总单元数量为165 988个，其中气囊为3 928个，氦气域为32 069个，空气域为129 991个。时间步长为1×10-4s，计算时间为0.5 s。气囊的泄气过程属于瞬态问题，打开大变形和动网格ALE开关。假设不可压缩气体，系统与外界没有热量交换，因此不考虑能量守恒方程。由于气囊内部氦气与外界空气之间存在质的交换，考虑组分守恒方程。本文采用湍流模型中的RNG模型，相应的计算参数取FLOTRAN给定的默认值。为了加快收敛速度，采用快速近似求解器求解压力和速度方程。为了保证求解稳定性，人工黏度取0.2以及压力松弛系数取0.8。

4.3 对比分析

基于本文建立的双向流固耦合方法计算得到的氦气囊形态变化趋势与本文试验结果基本保持一致。氦气从顶部区域的气嘴抽出时，囊体的收缩凹陷首先发生在下部区域，继而发生褶皱，相反，氦气囊顶部区域附近仍处于充盈状态；随着氦气的持续抽出，囊体的整体充盈度不断降低，囊体下部收缩凹陷程度不断增加，褶皱增多，形成复杂不规则的收缩凹陷，同时囊体下部区域的收缩凹陷状态逐渐扩展到上部区域，使得部分中、上部区域也产生收缩、凹陷和褶皱。在囊体的泄气过程中，其固定点处由于受到近似固端约束始终处于绷紧状态，其区域附近位移相对很小。

由于篇幅限制，本文仅给出充盈度分别为125%，80%，40%时，向量式有限元得到的氦气囊位移云图、ANSYS Flotran模块得到的压力云图以及模型试验拍摄的氦气囊形态，如图6～图8所示。将不同氦气充盈度下的氦气囊模型试验与数值分析结果相比较，得出泄气过程中的气囊形态变化规律是一致的，从而验证了本文提出的双向流固耦合方法的适用性和准确性。

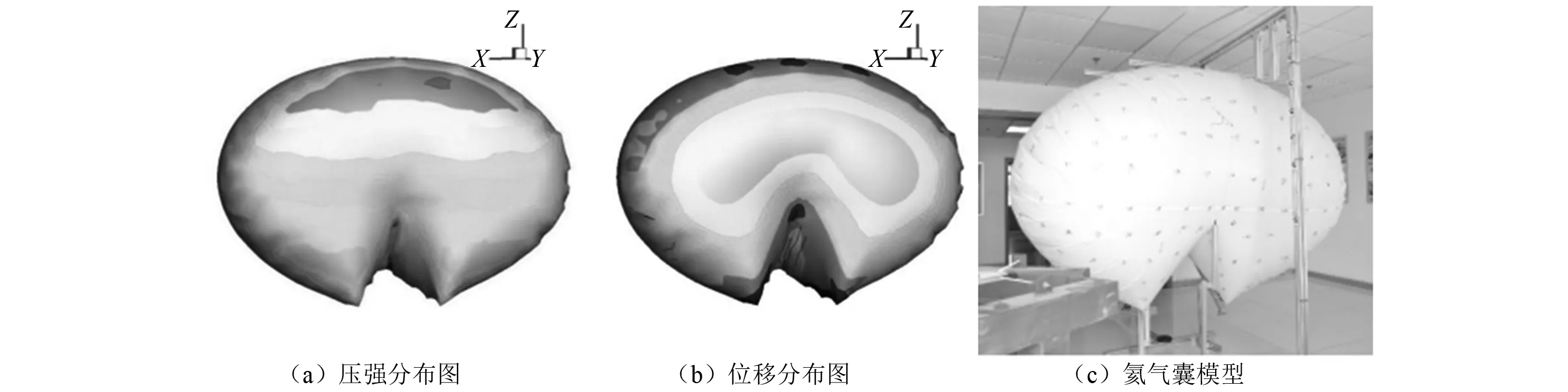
图6 充盈度为125%时流固界面传递信息Fig.6 Flow-solid transferred data at the filling ratio of 125%

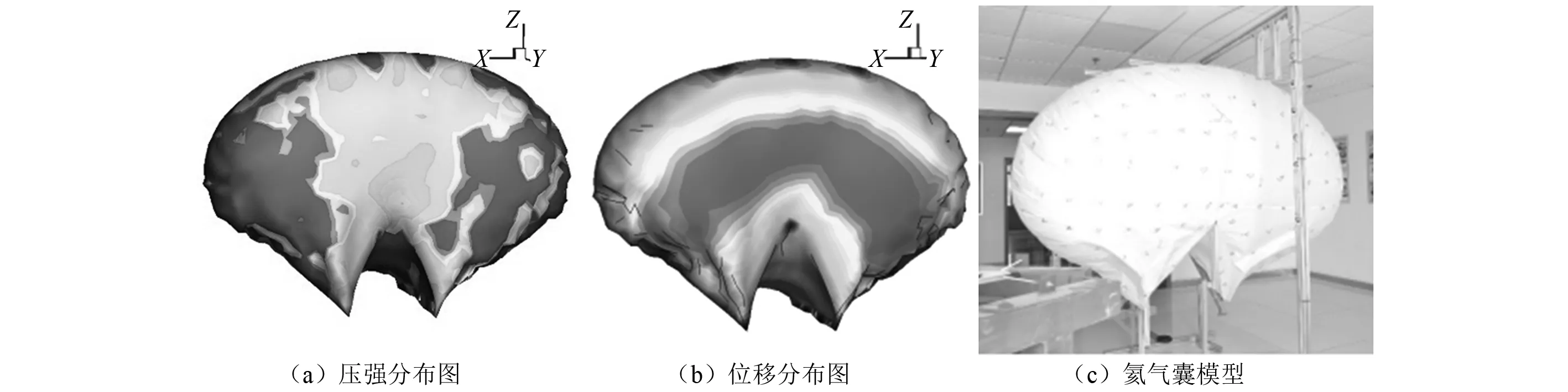
图7 充盈度为80%时流固界面传递信息Fig.7 Flow-solid transferred data at the filling ratio of 80%

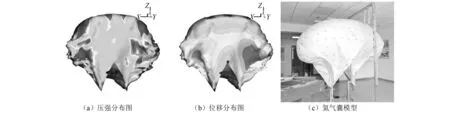
图8 充盈度为40%时流固界面传递信息Fig.8 Flow-solid transferred data at the filling ratio of 40%

图9(a)～图9(c)为三个靶点面(正、背、侧面)上选取的控制点相对初始状态的距离在泄气过程中的变化曲线。下横坐标是数值模拟结果中的氦气充盈度，而上横坐标是模型试验中的泄气序号。由于向量式有限元中的充盈度是根据每一步泄气时初始零压面的高度确定的，而迭代循环结束后的零压面高度往往发生微小变化，因此得到的氦气充盈度有±3%以内的误差。在模型试验中，理论上根据真空泵的流量(5 m3/h)可以算出抽取一定量的氦气需要的时间，从而控制每级泄气抽出的氦气体积。但是随泄气程度增大，抽气所需时间变长，利用真空泵的流量计算抽取出来的氦气体积的误差越来越大。因此模型试验和数值模拟的计算时刻不能一一对应。但是在同一张时间-位移图中可以看出，所有控制点随着氦气囊泄气程度的增大，其相对初始状态的距离变化趋势基本上保持一致，从而证明了本文提出数值模拟方法在研究气囊随氦气充盈度变化导致的非稳定形态变化规律的适用性。

图9 控制点相对初始状态的距离在泄气过程中的变化曲线Fig.9 Displacement of control points from initial state at different filling ratio

5 结 论

本文为揭示重载飞艇氦气囊力学行为，采用向量式有限元CSD和ANSYS Flotran的CFD，通过映射实现流固界面数据传递，考虑囊体大变形、褶皱、接触非线性和氦气浮力效应，建立了副气囊流固耦合数值模拟方法。对氦气囊泄气过程进行了数值模拟，得到了氦气囊在不同氦气充盈度下的形态变化规律，囊体底部区域随泄气首先发生收缩凹陷，顶部区域附近变形较小；随着泄气量增加，囊体沿高度方向从下至上依次收缩凹陷，凹陷之间产生挤压继而形成褶皱；囊体表面控制点随泄气程度的增大，其相对初始状态的距离呈现增大趋势，部分控制点在泄气过程中相对初始状态的距离会有小幅度的降低。同时开展了氦气囊的缩尺比例模型试验，对囊体在泄气过程中得到的位移测量值与数值模拟结果进行对比。结果表明，氦气囊在不同充盈度下的形态变化与双向流固耦合数值分析结果一致，证明了本文提出的数值模拟方法可有效用于气囊随氦气充盈度变化导致的非稳定形态变化规律的研究。