基于刚性块体模型的近-远场崩落矿岩流动特性

孙 浩，陈帅军，高艳华，金爱兵✉，覃 璇，巨 有，尹泽松，李木芽，赵增山

1) 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083 2) 北京科技大学土木与资源工程学院，北京 100083 3) 北京城市学院城市建设学部，北京 100083 4) 中国安全生产科学研究院，北京 100012 5) 鲁中冶金矿业集团公司，济南 271100

✉通信作者，E-mail：jinaibing@ustb.edu.cn

崩落采矿法尤其是自然崩落法的特点是连续回采，覆岩下放矿，以崩落覆岩充填采空区的方式管理地压，属于低成本、高效率的大规模采矿方法，在国内外金属矿山广为应用[1-2]. 依据崩落矿岩层高度或放矿高度的不同，可将地下金属矿山放矿问题划分为近场放矿(Near-field draw)与远场放矿(Far-field draw)两大类. 通常而言，将放矿高度小于100～200 倍矿岩颗粒平均粒径的放矿问题视为近场放矿，而将放矿高度大于100～200 倍矿岩颗粒平均粒径的放矿问题视为远场放矿[3].

目前，国内外学者针对金属矿山中近场放矿问题的室内试验、数值计算与理论研究等较为充分. 其中，在近场放矿理论研究方面，已形成椭球体理论[4]、类椭球体理论[5]、随机介质理论[6]、倒置水滴理论[7-8]等多种放矿理论，有力地促进了放矿理论和技术在金属矿山中的发展与完善. 而室内放矿试验手段受到众多学者青睐，在放矿领域研究中一直占据不可或缺的重要地位. 针对近场放矿问题，Čssr[9-10]、Janelid 和Kvapli[11]、Laubscher[12]、Power[13]、Castro 等[14]、陶干强等[15]、王洪江等[16]和Jin 等[8]在内的诸多学者利用不同相似比（1∶30 与1∶100）的物理模型，探究了颗粒粒径、矿岩层高度、放矿口尺寸和垂直应力等不同因素影响下的崩落矿岩运移规律. 王云鹏和余健[17]、邵安林[18]、徐帅等[19]、Castro 和Pineda[20]以及孙浩等[21]在内的诸多学者基于分段高度、进路间距、崩矿步距和端壁倾角的不同组合，开展了程潮铁矿、首云铁矿、金厂沟梁金矿、加拿大Agnico Eagle 金矿和梅山铁矿等崩落法金属矿山的采场结构参数优化试验研究. 此外，随着计算机技术和放矿理论的不断发展，数值模拟方法将在放矿问题研究中发挥更为关键且不可或缺的作用，其中基于颗粒离散元的PFC 软件因其能够从细观角度分析矿岩散体介质的移动规律，适用于放矿问题研究[22-23]. 目前，国内外学者已基于PFC 软件在金属矿山近场放矿问题研究中取得诸多成果. Hashim[24]通过室内放矿试验量化了放出体(Isolated extraction zone，IEZ)与松动体(Isolated movement zone，IMZ)内的剪切应变，并利用PFC 程序研究了颗粒形状、块度分布等因素对小粒径颗粒穿流特性的影响. Song 等[25]利用PFC 软件研究了颗粒形状对放出体形态的影响. 胡建华等[26]采用正交数值仿真和盈利因子评价函数，进行分段高度、进路间距、崩矿边孔角、截止贫化率的四因素三水平正交数值模拟，探究矿岩颗粒流动规律，确定了最优采场结构参数组合. 孙浩等[27-29]基于PFC 程序中的球形颗粒研究三类边界条件下的矿岩颗粒移动规律，实现了放出体、矿石残留体形态变化过程的可视化.

目前，如南非的Cadia Valley 铜金矿、中国的普朗铜矿等国内外自然崩落法矿山的矿岩层高度均已超过200～300 m，属于典型的地下金属矿远场放矿问题. Castro 等[30]利用室内试验手段研究了远场放矿中不同放矿方式下底部结构所承受垂直应力的变化规律. Rafiee 等[31]利用离散元数值模拟手段研究了远场放矿前不同因素影响下的矿岩可崩性，发现：原位应力和水力半径是自然崩落法中影响矿岩可崩性的主要因素. 然而，无论是现行放矿理论、室内试验还是数值模拟研究，对于远场中松动体、放出体形态演化规律尚未形成统一认识，崩落矿岩运移机理研究尚不深入，这也导致放矿理论与方法的发展相对缓慢，一定程度上限制了崩落采矿法尤其是自然崩落法在我国地下金属矿山中的应用. 因此，本文综合利用放矿物理试验、数值模拟以及理论分析等手段，探究基于刚性块体模型的金属矿山近-远场矿岩颗粒流动特性，为崩落法矿山结构参数优化以及矿产资源的安全高效开采提供理论与技术支持.

1 近场放矿试验

1.1 近场放矿模型构建

本文首先通过对比近场条件下放矿物理试验与数值试验结果，检验近场放矿模拟的可靠性，分析近场条件下的矿岩颗粒流动特性，为远场放矿研究奠定基础.

（1）近场放矿模型设计.

本次近场室内试验采用如图1（a）所示自主研制的能够满足不同相似比的大型三维放矿物理试验平台，材质为PVC 和有机玻璃. 模型最大高度为2.5 m，模型内可装填尺寸为长×宽×高=0.8 m×0.8 m×2.0 m. 本次试验设计为相似比1∶25 的单口底部放矿试验（模拟实际50 m 的放矿高度），放矿口位于模型底部中心位置，其尺寸为0.12 m×0.12 m.

图 1 三维放矿物理与数值模型. （a）放矿物理试验平台；（b）放矿数值模型Fig.1 3D physical and numerical draw models: (a) physical draw test platform; (b) numerical draw model

本次近场放矿数值模型为原位模型（图1（b）），与物理试验模型呈几何相似，即数值模型尺寸较物理模型尺寸扩大了25 倍. 模型底部中心位置的红色墙体为出矿结构，放矿模拟开始前将其删除即可形成放矿口.

（2）近场放矿试验材料.

因本次研究问题为矿岩散体流动特性，故物理试验中散体材料及标志颗粒均选用密度相对较小且易得的建筑用石灰石颗粒（图2（a））.

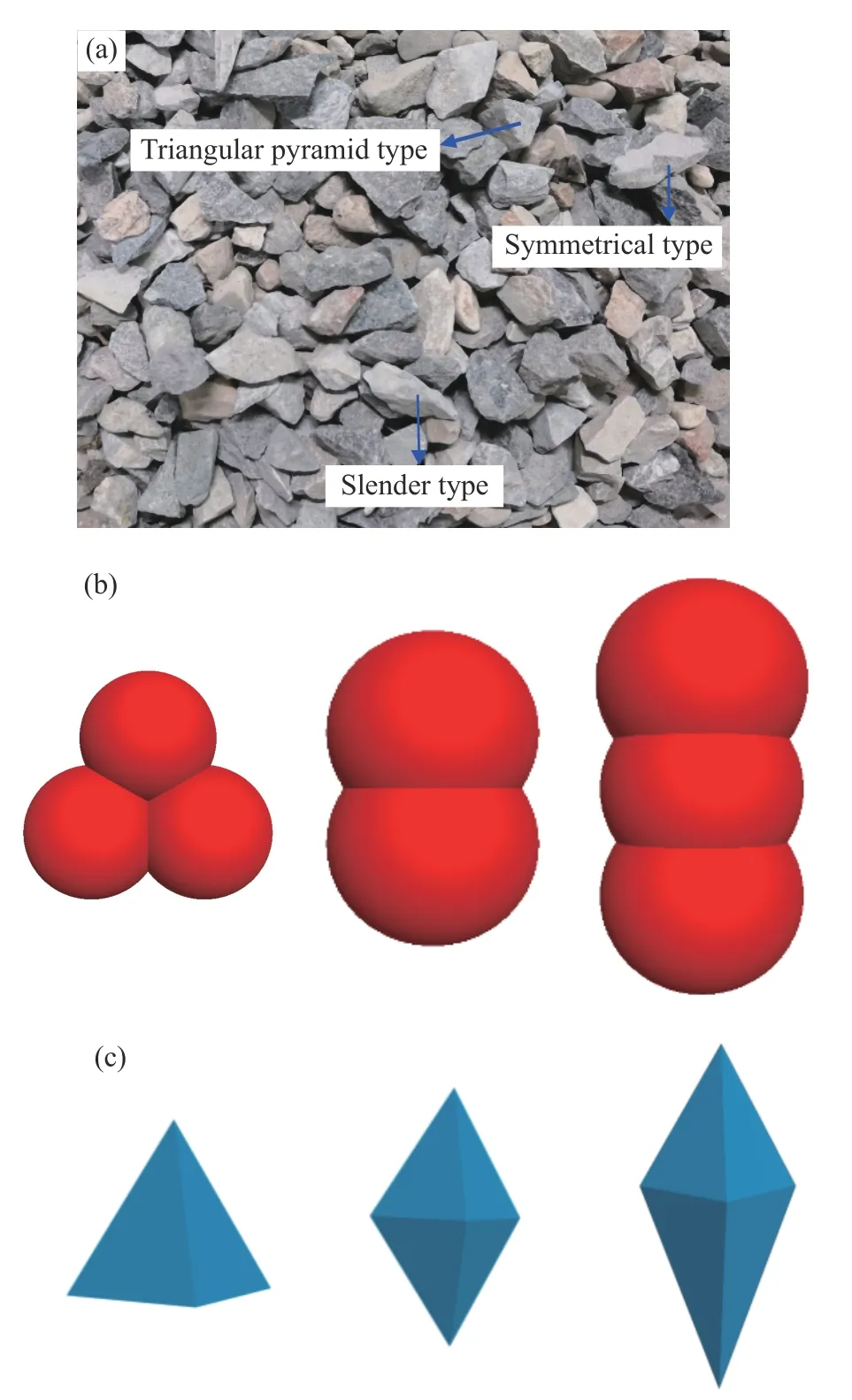
图 2 物理与数值试验中的三维颗粒形状. （a）物理试验中存在的颗粒形状；（b）过往数值模拟中选用的颗粒形状；（c）本次数值模拟中选用的颗粒形状Fig.2 3D particle shapes used in physical and numerical draw tests: (a)particle shapes in the physical test; (b) particle shapes used in previous numerical simulations; (c) particle shapes used in these numerical simulations

在过往基于PFC、EDEM 等颗粒离散元软件研究放矿问题时，通常采用球形颗粒或由若干球形颗粒组成的颗粒簇(Clump)（图2（b））模拟真实矿岩，但球形颗粒因其表面过于光滑而无法提供颗粒间足够的内锁力，从而无法定量、准确表征放出体与松动体形态及其变化规律. 若不能有效提高放矿模拟结果的可靠性，后续将难以进一步定量分析崩落矿岩运移演化规律及其力学机理. 因此，本次数值试验采用PFC 软件中的刚性块体模型(Rigid block model)[32]构建如图2（c）所示的三种不同长宽比的不规则块体模拟三棱锥型、对称性和细长型等真实矿岩形状. 此外，除了提升矿岩散体形状模拟的准确性，与颗粒簇模型相比，基于刚性块体模型开展放矿问题研究的另一优势为计算效率的提升：在PFC 中，每一个刚性块体或球形颗粒均可视为1 个独立的组元(Piece)，即与其他组元之间仅存在1 个接触(Contact)，而由N 个球形颗粒组成的颗粒簇与其他组元之间则存在N 个接触.因此，颗粒或块体间接触数目的大幅减少可有效提高放矿模拟效率.

放矿物理试验和数值试验中的颗粒级配曲线如图3 所示. 其中，物理试验中散体材料粒径为3～45 mm，平均粒径为19.2 mm，筛分后的不同粒径石灰石散体如图4 所示；数值试验中的颗粒粒径分布与物理试验一致，两者间的相似比同样为1∶25，且所用的三种不同形状刚性块体（图2（c））的数量相同，各占总块体数量的1/3.

（3）近场放矿试验过程.

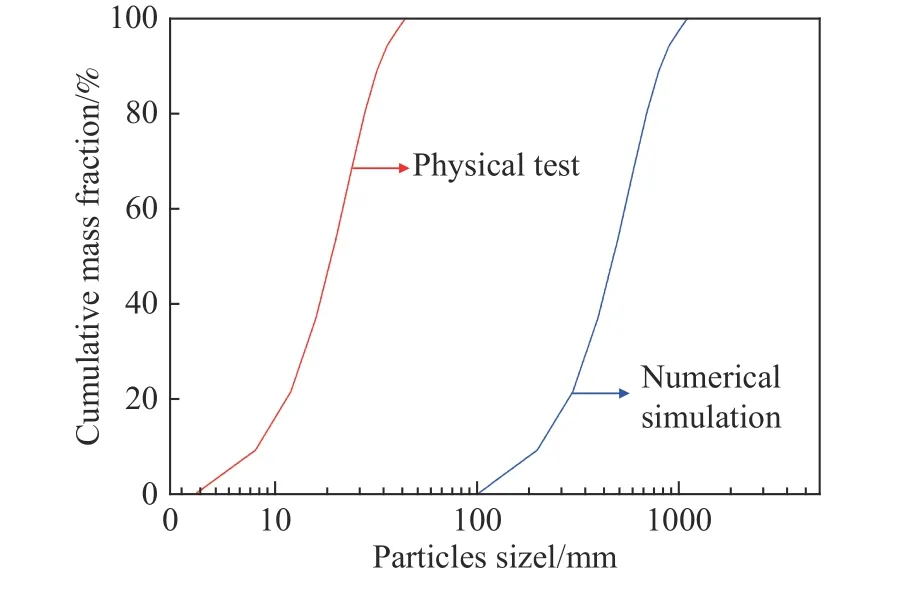
图 3 物理与数值试验中的颗粒级配曲线Fig.3 Particle size distribution curves in physical and numerical draw tests

本次物理试验中散体材料的装填高度为2.0 m，并在模型内垂直方向上每隔0.1 m 布设一层标志颗粒（图5），采用标志颗粒法[8]圈定放出体形态.试验中通过在模型顶部补充散体材料的方式，保证放矿过程中矿岩层高度不变，当放矿高度达2.0 m时停止出矿. 由于三维物理模型内部的矿岩颗粒运移过程难以直接观测，故本次放矿物理试验中并未测量和圈定松动体形态.

图 4 筛分后所得不同粒径的石灰石散体. （a）3～8 mm；（b）8～16 mm；（c）16～25 mm；（d）25～45 mmFig.4 Limestone particles with different sizes after sieving: (a) 3-8 mm; (b) 8-16 mm; (c) 16-25 mm; (d) 25-45 mm

图 5 标志颗粒布设图Fig.5 Layout of labeled markers

本次近场放矿数值试验过程与物理试验保持一致，当放矿高度达50 m 时停止出矿. 首先通过编译程序记录每个刚性块体在放矿开始前的初始空间坐标，在放矿模拟过程中通过反演某一时刻全部已放出块体的初始位置即可形成该时刻下的放出体形态. 由于后续研究中仅需关注放出体的整体高度、宽度及形态演化规律，并不关注单个放出刚性块体的形状和空间排布形式，因此，为了提高运算效率，本次模拟中反演所得放出体均由与不规则刚性块体等体积的球形颗粒组成. 而放矿过程中由空间位置发生变化的矿岩散体组成的空间形态即为松动体，故本次模拟所得松动体均由不规则刚性块体组成. 此外，放矿数值试验中墙体和刚性块体的细观力学参数取值如表1 所示. 其中，若墙体和刚性块体的法向与切向刚度过小，则块体-块体间以及块体-墙体间均会产生过度的相互重叠量，过大的话则影响运算时步(Timestep)，从而显著降低计算效率；此外，墙体刚度需略大于块体刚度，以避免出现块体“穿墙”的错误. 刚性块体密度与物理试验中所用石灰石散体的密度一致，取2620 kg·m-3. 通过对比自然安息角[33]物理试验与数值试验结果，确定本次放矿模拟中墙体及刚性块体的摩擦系数均取0.5.

表 1 墙体及刚性块体细观力学参数Table 1 Meso-mechanical parameters of walls and rigid blocks

1.2 近场放矿试验结果分析

放出矿岩散体在崩落矿岩初始堆积体系中所占空间位置组成的形态为放出体，而崩落矿岩堆积体系中所有发生移动的矿岩散体组成的空间形态为松动体[34]. 统计放出散体总质量和放出标志颗粒的位置信息，基于插值法圈定如图6（a）所示的物理试验所得不同高度的放出体；图6（b）和图6（c）分别为数值试验所得高度为50 m 的放出体和松动体. 由图6 可知：物理试验与数值试验所得放出体、松动体形态均呈倒置水滴形[8]，即从定性角度证明了刚性块体模型在放矿数值研究中的适用性.

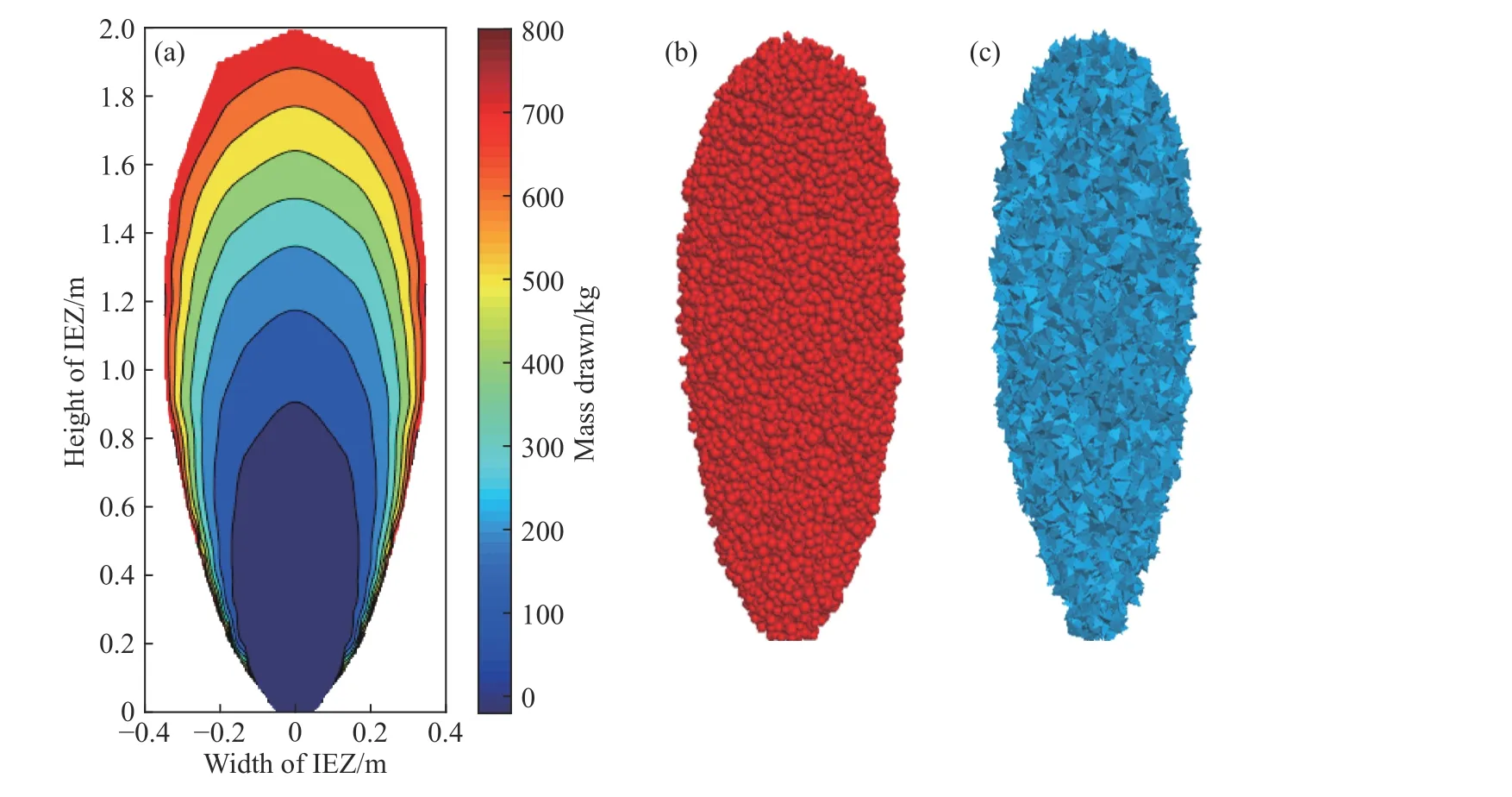
图 6 放矿物理与数值试验中的放出体与松动体形态纵剖面图. （a）物理试验中的放出体；（b）数值模拟中高度50 m 的放出体；（c）数值模拟中高度50 m 的松动体Fig.6 Longitudinal profiles of the IEZ’s and IMZ’s shapes in physical and numerical draw tests: (a) IEZ in the physical test; (b) IEZ with a height of 50 m in numerical simulation; (c) IMZ with a height of 50 m in numerical simulation

统计物理试验与数值试验中不同高度时放出体与松动体的最大半径（最大宽度的一半），得到如图7 所示的放出体、松动体高度与其最大半径的拟合曲线.

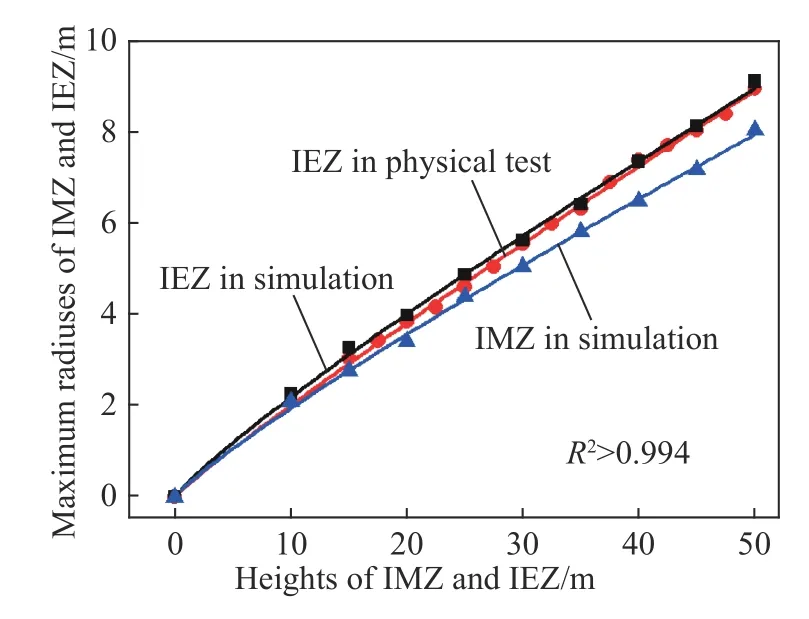
图 7 放出体、松动体高度与最大半径关系的近场放矿物理与数值试验结果对比Fig.7 Comparison of relationship between the height and maximal radius of IEZ/IMZ in near-field physical and numerical draw tests

由图7 可知：近场条件下物理试验与数值试验所得放出体与松动体的高度与其最大半径之间均满足倒置水滴理论[8]所述幂函数关系（式（1）），三条曲线的拟合优度R2均大于0.994：

式中，rmax为放出体/松动体的最大半径，H 为放出体/松动体的高度，a 和b 为拟合常数.

如图7 所示，同一放出体高度时，数值试验与物理试验所得放出体最大半径基本一致，即从定量角度证明了刚性块体模型在放矿数值研究中的可靠性. 此外，同一高度时，松动体的最大半径明显小于放出体的最大半径. 这是由于松动体一直被视为放出体的先驱(Precursor)[35]，即松动体与放出体的形态变化规律一致，且同一高度时的松动体比放出体的产生时刻要早，如本次数值试验中当松动体高度达50 m 时，放出体高度仅达23.7 m.随着放矿过程的不断推进，矿岩颗粒体系结构愈加松散，故同一高度时松动体的最大宽度小于放出体的最大宽度.

2 远场放矿数值试验研究

在近场放矿物理试验与数值试验研究的基础上，进一步开展基于刚性块体模型的远场放矿数值试验研究，分析远场条件下的矿岩颗粒流动特性.

2.1 远场放矿数值试验设计

采用与近场放矿数值试验中相同的三种刚性块体形状（图2（c））、级配曲线（图3）和细观力学参数（表1），构建如图8 所示的长×宽×高=60 m×60 m×105 m 的放矿数值模型，模型高度约为刚性块体平均粒径（0.48 m）的220 倍，符合远场放矿要求[3]. 在模型内不同位置布设如图8 所示的直径6 m的9 个测量球域，监测放矿过程中不同空间位置块体所受水平与垂直应力的变化过程. 其中，1、4、7 号测量域分别布设于离底部放矿口正上方20、55 和90 m 处，即放矿模型中轴线穿过上述三个测量球域的球心；而同一高度相邻测量域的布设间距为12 m. 综合考虑松动体与放出体形态变化规律的一致性以及计算时间问题，本次远场放矿数值试验仅模拟至松动体高度达105 m，分析整个松动体的形态变化规律并基于应力监测结果分析远场条件下矿岩颗粒流动特性及其力学机制.

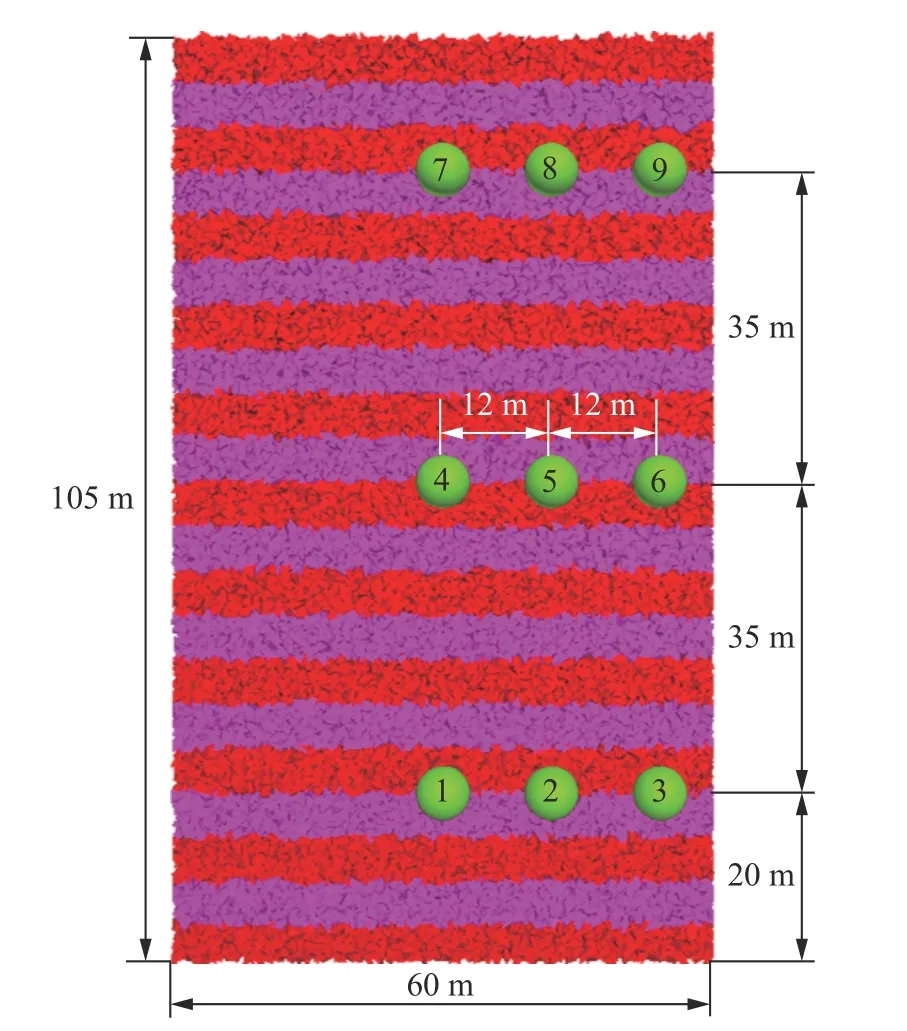
图 8 远场放矿数值模型纵剖面图和应力测量域布设Fig.8 Longitudinal profile of the far-field numerical draw model and layout of stress measurement regions

2.2 远场放矿数值试验结果分析

统计远场放矿数值试验中不同高度时松动体的最大半径，得到如图9 所示的松动体高度与其最大半径的拟合曲线，以及35、65 和95 m 等不同高度时的松动体形态. 由图9 可知：远场条件下的松动体形态依然符合倒置水滴形，且松动体高度与最大半径之间亦满足倒置水滴理论所述幂函数关系（式（1）），其拟合优度R2为0.996. 在放矿初始阶段即松动体顶部距放矿口较近时（＜25 m），放矿口对松动体形态变化的影响较为显著[27]，松动体最大宽度随高度增大而快速增加；在之后的放矿阶段尤其是远场放矿过程中，松动体形态变化主要受矿岩颗粒自身物理力学性质和整个矿岩颗粒体系应力状态的影响，松动体最大宽度随高度增大而近似线性增加. 因此，针对放矿高度较大（＞100 m）的大型自然崩落法矿山，远场条件下松动体高度与最大宽度间的近似线性关系更有利于放矿口间距等采场结构参数的设计与优化.

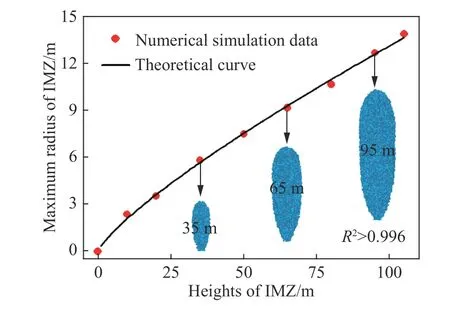
图 9 松动体高度与最大半径关系的远场放矿数值模拟数据和理论曲线对比Fig.9 Comparison between the data of far-field numerical draw test and theoretic curve for the relationship between the height and maximal radius of IMZ

统计整个放矿过程中如图8 所示的9 个不同空间位置测量球域内刚性块体所受水平与垂直应力的变化过程. 其中，图10 为第1、4、5、6、7 号测量域内垂直应力变化过程. 在放矿初始阶段，如图10 中第1、4、7 号曲线所示，上覆矿岩层越高的刚性块体所受垂直应力越大；而如图10 中第4、5、6 号曲线所示，同一高度水平的刚性块体所受垂直应力无明显差距. 此外，当矿岩散体松动范围未波及相应测量域时，其垂直应力无明显变化（6 号曲线）；反之，相应空间位置的垂直应力均出现明显降低.

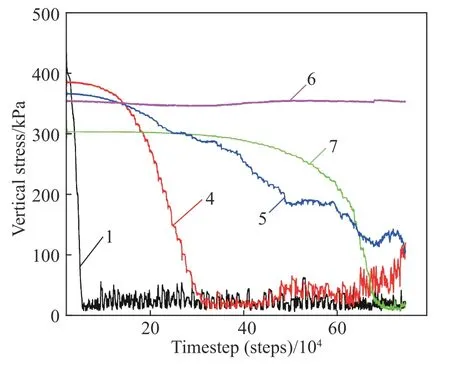
图 10 第1、4、5、6、7 号测量域内的垂直应力变化过程Fig.10 Variations of vertical stresses within measurement regions Nos.1, 4, 5, 6, and 7

图11 为位于模型中轴线上不同高度的第1、4、7 号测量域内水平应力变化过程. 如图11 所示：① 在放矿初始阶段，当矿岩散体松动范围尚未发展至第1 号测量域所在高度前，模型内某处上覆散体越厚，该处矿岩颗粒所受水平应力越大；②当矿岩散体松动范围未达第4 号或第7 号测量域所在高度前，其水平应力无明显变化；③ 当矿岩散体松动范围依次达到第1、4、7 号测量域所在高度时，其水平应力均出现如图11 中绿色圆圈所示的急剧增大；④ 当矿岩散体松动范围依次超过第1、4、7 号测量域所在高度后，即所在高度的矿岩颗粒已处于较松散状态时，其水平应力均出现急剧下降.

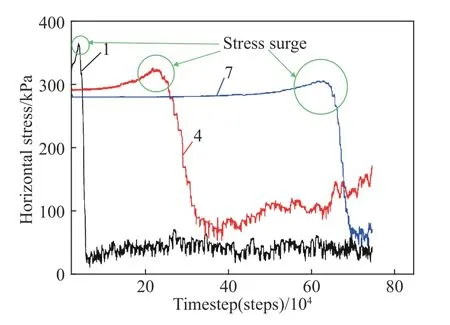
图 11 第1、4、7 号测量域内的水平应力变化过程Fig.11 Variations of horizontal stresses within measurement regions Nos. 4, 5, and 6

侧压力系数能够反映矿岩颗粒体系内不同空间位置水平应力与垂直应力的相互关系. 鉴于松动体内垂直应力较小，考虑到图片的直观性，故本次分析取侧压力系数的倒数，即垂直应力与水平应力之比. 图12 为第4、5、6 号测量域内侧压系数倒数的变化过程. 如图12 所示，当矿岩散体松动范围未达第4 号测量域所在高度前，其垂直应力与水平应力之比明显减小；随后，第4 号测量域所在位置进入松动体范围内，其垂直应力与水平应力之比呈波动变化的趋势. 当矿岩散体松动范围逐步波及第5 号测量域所在位置时，其垂直应力与水平应力之比逐渐增加；随后，第5 号测量域所在位置进入松动体范围内，其垂直应力与水平应力之比呈明显降低的趋势. 此外，第6 号测量域在整个放矿过程中均处于非松动区域，其垂直应力与水平应力之比呈逐步增大的趋势.

3 讨论

放矿过程中矿岩颗粒流动体系内存在明显的拱结构(Arch structure)，即颗粒体系能够通过相互支撑的方式形成稳定结构的现象[36]. 形成拱结构的矿岩散体间可承受一定应力而处于稳定状态，因此，拱结构亦可称为应力拱(Stress arch). 应力拱的形成、演化与崩塌会主导崩落矿岩的运移过程[3,35].针对上述分析所得松动体形态变化规律和应力演化规律，从应力拱与应力转移（图13）角度对其力学机制作如下讨论：

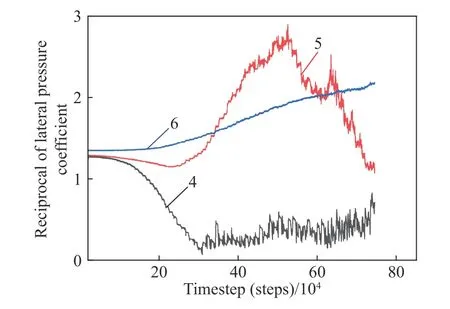
图 12 第4、5、6 号测量域内侧压系数倒数的变化过程Fig.12 Variations of reciprocal of the lateral pressure within measurement regions Nos. 4, 5, and 6

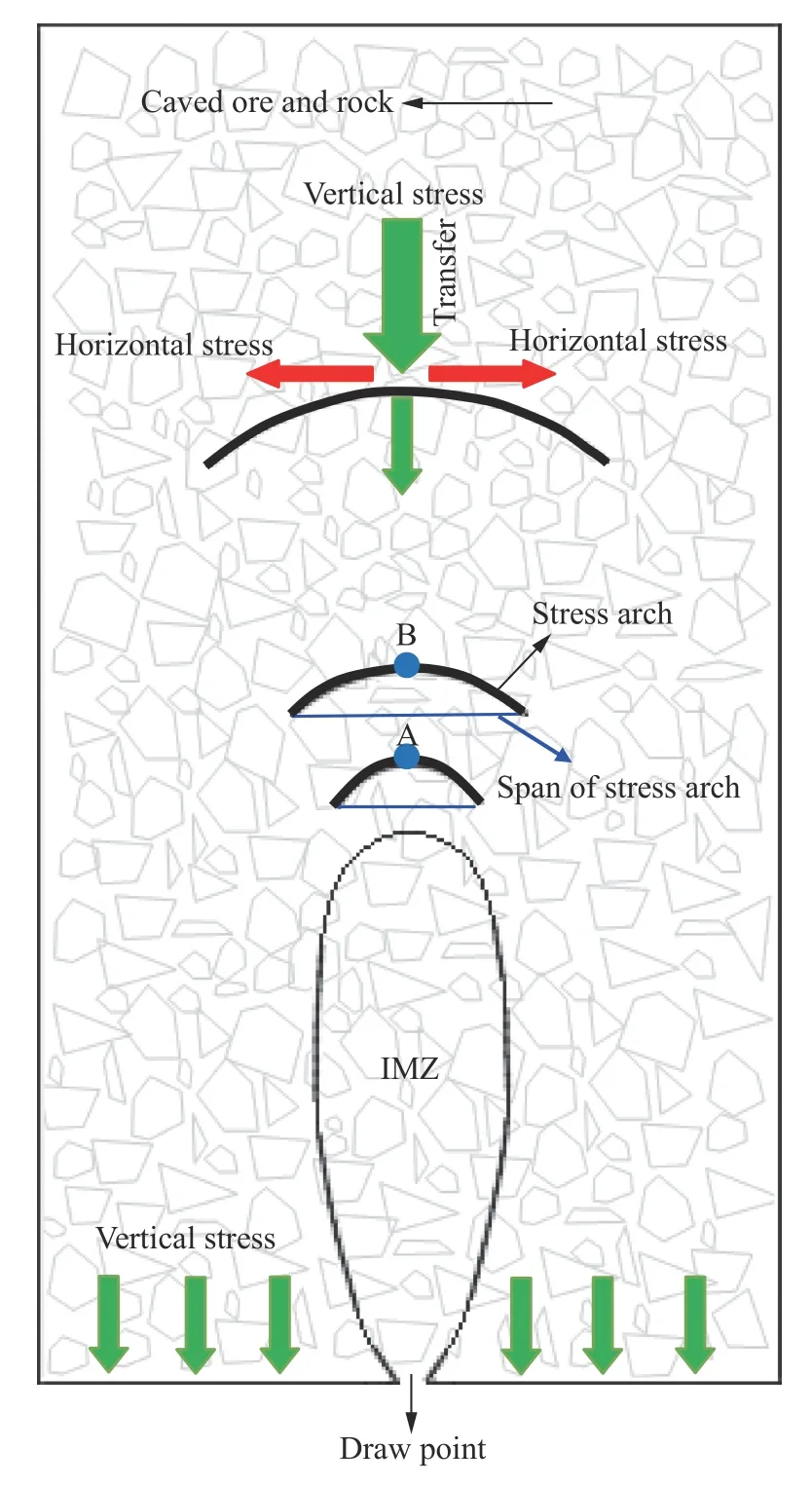
图 13 矿岩颗粒流动体系内应力拱和应力转移示意图Fig.13 Schematic of stress arch and stress transfer within the particle flow system of caved ore and rock

（1）对于无限边界条件下的单口放矿问题而言，放矿开始前模型底部不同位置所受到的由上覆矿岩自重产生的垂直应力基本相同. 随着放矿过程的开始，放矿口的存在将导致模型底部垂直应力向放矿口两侧区域转移并逐渐加强，从而在放矿口上方一定高度范围内形成若干应力拱. 如图13 所示，应力拱的存在致使A 点的垂直应力并非其全部上覆矿岩自重，而是相邻两应力拱间（AB 两点间）矿岩散体自重产生的垂直应力. 随着A 点上方应力拱的不断形成与加强，A 点的垂直应力出现如图10 所示不断减小的现象；与其同时，A 点上方垂直应力经由应力拱（散体间接触力链）向两侧转移，从而致使A 点的水平应力不断增大，尤其当松动体顶部接近A 点时，该点的水平应力出现如图11 所示的应力激增现象. 如图12 所示的不同位置垂直应力与水平应力之比的不断变化即证明矿岩颗粒流动体系内应力转移现象的存在.

（2）当图13 中A 点应力超过该处应力拱的承载极限时，组成该应力拱的矿岩散体间的关键接触出现断裂，应力拱崩塌，A 点矿岩散体随之进入松动区域，松动体因而不断向上发展. 随着松动区域不断扩大，松动体上方的应力拱跨度随之不断增大，即组成该应力拱的矿岩散体间的最大宽度不断增大，上述矿岩散体将在应力拱崩塌后发生移动，从而逐渐形成倒置水滴形的松动体形态.Čssr[9-10]和Janelid 等[11]最初以砂子作为介质进行放矿物理试验，发现放出体与松动体形态近似一个椭球体. 然而，与砂子相比，矿岩散体的粒径与形状具有明显不均匀性，从而导致颗粒间的内锁力更大，崩落矿岩流动过程中的应力拱效应更为显著，因此形成的松动体形态更接近倒置水滴形而非椭球体.

后续作者将利用室内试验与数值模拟等手段，进一步探究矿岩颗粒流动体系内接触力链、应力状态与拱形结构等力学状态量的演化规律，并利用流变学与统计力学相关原理，从宏-细观角度分析矿岩颗粒流动体系的结构非均匀性特征和颗粒间动力学行为，从力学角度揭示矿岩颗粒流动体系结构的形成机理.

4 结论

（1）通过放矿物理试验与数值模拟结果的对比分析，证明了刚性块体模型在崩落矿岩流动特性研究中的可靠性与优越性. 该模型可用于后续更复杂条件下矿岩颗粒流动体系的结构特征及形成机理研究.

（2）近-远场条件下的松动体形态变化均符合倒置水滴理论. 在放矿初始阶段，松动体最大宽度随高度增大呈幂函数形式快速增加；随后，松动体最大宽度随高度增大而近似线性增加. 因此，远场条件下松动体高度与最大宽度间的近似线性关系更有利于指导大型自然崩落法矿山的采场结构参数优选.

（3）崩落矿岩流动过程中存在明显的应力拱效应. 随着矿岩散体松动范围不断扩大，松动体外围一定范围内的垂直应力均呈明显下降趋势，水平应力逐渐增大并在松动区域到达前出现激增现象；而松动体内的水平应力与垂直应力则急剧下降至较低水平.