Medical Treatment Process Modeling Based on Process Mining and Treatment Patterns

Liqin Yang,Guosheng Kang,Liang Zhang

1 School of Computer Science,Fudan University,Shanghai 200438,China

2 Shanghai Key Laboratory of Data Science,Shanghai 200438,China

3 Institute of Intelligent Electronics and Systems,Shanghai 200438,China

4 Computer Teaching and Research Section,Shanghai University of Traditional Chinese Medicine,Shanghai 201203,China

5 School of Computer Science and Engineering,Hunan University of Science and Technology,Xiangtan 411201,China

Abstract: Clinical practice guidelines (CPGs) are statements relating to evidence-based and economically reasonable medical treatment processes(MTPs)for certain clinical circumstances.The executable MTPs in healthcare information systems can assist the clinical processes.In our previous work,several treatment patterns and their modeling proposals were proposed to reduce the effort spent in modeling MTPs.However,given a CPG document,all the process elements are modeled manually.Besides, business process mining can extract MTP models automatically from execution logs.However, the existing process mining algorithms focus on the control-flow of structured processes.This paper proposes an integrated framework for modeling executable MTPs based on process mining and treatment patterns,taking both the efficiency of mining and the quality of modeling into account.In this framework,an execution log processing approach is presented to identify the subsequences and decision points conforming to the treatment patterns and represent them with abstract activities.Experiments on a synthetic log of the non-secondary hypertension MTP and empirical findings demonstrate the effectiveness of our approach.The results show that the process mining in our approach framework can automatically generate more accurate MTP models,and the subprocess models based on treatment patterns make the models easy to understand.

Keywords:business process modeling;medical treatment processes; treatment patterns; clinical practice guidelines

I.INTRODUCTION

Clinical Practice Guidelines (CPGs) are systematically developed statements that describe evidencebased and economically reasonable medical treatment processes(MTPs),aiming at improving the quality of care, limiting unjustified practice variations and reducing healthcare costs [1].Developing an information system based on such MTPs will support medical workers carrying out CPGs more effectively.Business process modeling technologies have been utilized to model MTPs that will be directly executed by workflow engines [2–4].Different from general business processes, MTPs are usually flexible (i.e.including unstructured process segments) [5] and knowledgeintensive [6] (i.e.including quite a lot of diagnosis decision logic and time constraint medical activities).These characteristics result in complicated MTP models.Thus modeling MTPs becomes a difficult and demanding task.To reduce the effort spent in modeling,a treatment pattern based modeling approach is proposed for modeling MTPs in a CPG document [7].Treatment patterns are generic process segments of frequent behaviors in MTPs.Modelers can apply the treatment patterns as templates and configure them to form process model segments conveniently.However,the number of MTPs included in a CPG document is very large,and each process may contain a lot of medical activities, so modeling all process elements in a CPG document manually will affect the efficiency.

Business process mining can extract MTP models automatically from CPG compliant execution logs[8–10].The existing process mining algorithms focus on the control-flow perspective of structured business processes.Business rules(e.g.detailed decision logic)are covered by the control-flow so that the generated MTP models cannot be directly executed by workflow engines.Besides, if an MTP includes unstructured process segments, a spaghetti-like model may be obtained that is difficult to understand and maintain.To deal with the flexibility of MTPs, instances(also referred to traces) in logs are divided into different groups using clustering techniques, and then a process mining algorithm is performed on each group to generate a relatively simple process model[11,12].However,each MTP model corresponding to a sublog just reflects a partial process about one aspect.

To improve the efficiency of treatment pattern based modeling and address the limitations of process mining,this research proposes an integrated MTP modeling approach based on process mining and treatment patterns.Firstly, structured parent MTP models are mined from abstracted logs automatically.Then,subprocesses included in the parent models are modeled using treatment patterns as templates in accordance with CPGs.Specifically, the novel contributions of this research are as follows:

• An integrated framework for modeling executable MTPs based on process mining and treatment patterns is proposed that uses process mining to obtain structured parent MTP models from logs automatically and configures the treatment patterns to model the corresponding subprocesses according to CPGs.The semi-automatic modeling approach integrates the advantages of process mining and treatment pattern based modeling,taking both efficiency and quality into account.

• This work presents an execution log processing approach for simplifying logs so that process mining algorithms will be performed on the simplified logs to get structured parent MTP models.The approach identifies subsequences and decision points conforming to treatment patterns and represents them with abstract activities.The process mining algorithms will grain better results on such simplified logs.

• Experiments performed on a synthetic log of the non-secondary hypertension MTP validate the effectiveness of our approach.Feedback from interviewed physicians shows that the behaviors expressed in the resulted MTP model are in accordance with the expressions described in CPGs.

The rest of this paper is organized as follows.Section II introduces the related work of this research.Section III presents the MTP modeling framework based on process mining and treatment patterns.The detailed treatment pattern descriptions and their realizations are presented in Section IV.Section V exposes the log processing approach based on treatment patterns.Section VI reports the evaluations of our approach,followed by the conclusion in Section VII.

II.RELATED WORK

There are many attempts to apply business process mining and modeling technologies to obtain MTP models.Because of the characteristics of MTPs,adoption of these technologies on MTPs is faced up with new challenges.In this section,we present the related research on MTP mining and modeling respectively.

2.1 Business Process Mining for MTPs

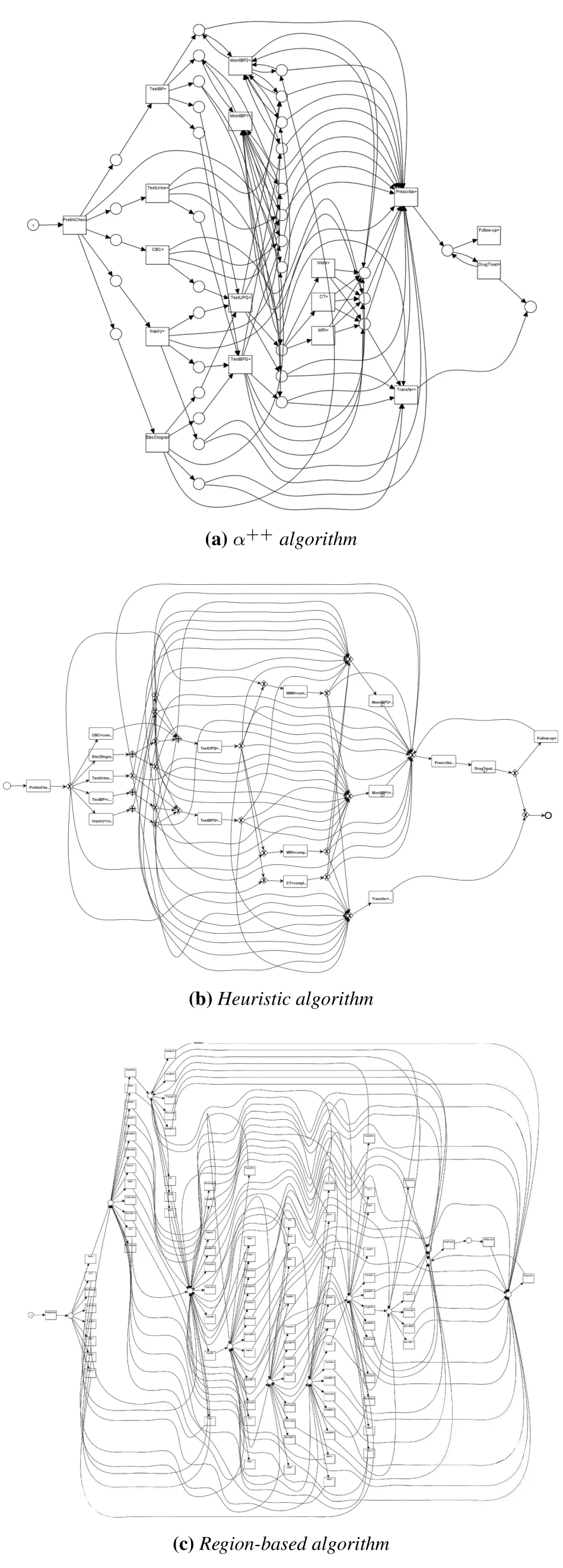
Business process mining is a methodology to discover business process models from event logs that record their executions.One important aspect is control-flow discovery, i.e.automatically constructing a process model describing the causal dependencies between activities.Many process mining algorithms [8–10, 13]have been developed in nearly two decades,and each of them has its own advantages and limitations.Due to the flexibility and diversity of MTPs,any single algorithm directly performed on clinical data will not produce ideal MTP models.Martin et al.[9] evaluated the performance of seven traditional process mining on clinical data.The result showed that none of them could produce an ideal MTP model because of the complexity of clinical data.The work in [5] utilized Heuristic Miner[10]in ProM framework[14]to recognize the typical path for 627 gynecological oncology patients.It got a spaghetti-like model from the billing data,which was difficult for understanding.

To deal with the flexibility of MTPs, one kind of approach is to divide logs into different groups using clustering techniques,and then a process mining algorithm is performed on each group to generate a relatively simple process model.Ghattas et al.[11]organized process instances into different groups according to their similarity of paths and outcomes.Zhang et al.[12] utilized hierarchical clustering based on the longest common subsequence distance to group instances of chronic kidney disease into six subgroups.However, each MTP model corresponding to a subgroup just reflects a partial process about one aspect.Another kind of approach is to package correlate events into new units to reduce the number of activities in the log for further mining.Perer et al.[15]used Apriori algorithm to find frequent itemsets of clinical events in the log.All the events in one set are considered as a“super event”,and then they continued to use Apriori algorithm to get a higher level of“super event”for the simplified log.Jin et al.[16]proposed a twolevel packing strategy based on conditional probability to construct clinical-event-packages with correlate events.However, these correlate events are just discovered based on logs so that they do not necessarily express meaningful business behaviors.The treatment patterns [7] of our approach are meaningful business behaviors relating to medical domain,because they are extracted directly from various MTP models.

2.2 Business Process Modeling for MTPs

Business process modeling is a methodology to represent an MTP model with some business process modeling language.Among the, the BPMN (Business Process Modelling Notation) [17] is becoming more popular in clinical settings as recent literature shows[2, 3].Most of these works agreed in emphasizing that BPMN is easy to use and to understand by all stakeholders.However, BPMN is not capable of describing the highly flexible and variable medical treatment processes.Therefore, the Object Management Group (OMG) published the CMMN (Case Management Model and Notation)[18]to complement BPMN with capabilities for constructing weakly structured processes influenced by the information flowing into the case.CMMN models possible activities and the limits on activities.It models when the activities may take place,when they must take place,and when they must not take place.Moreover, complex diagnostic decision logic represented through control-flow structures results in extremely complex models that are difficult to understand.The OMG published DMN(Decision Management Notation) [19] in 2015 providing decision tables and decision requirement diagrams to support the complex decision making in the medical domain.Works in [20–22] agreed that medical treatment process models represented with the combination of BPMN, DMN and CMMN are easy to understand and maintain.A complete treatment process is represented as a BPMN model, and the included Task and Subprocess [17] elements can be modeled with BPMN, DMN or CMMN.Specifically, a DMN model can be invoked by a Business Rule Task[17];a CMMN model can be invoked by a Call Task [17]; a BPMN model can be embedded in a Subprocess element.Camunda[23]provides an integrated modeling platform and execution engine supporting these three languages simultaneously.

Given a CPG document, modeling all the medical treatment processes is not a straightforward task.To alleviate the burden for modeling, applying patterns helps human modelers in establishing a set of modular components for generating process models [24].Russell et al.proposed workflow patterns[25]to support general process modeling.However, some common medical process patterns needed for medical domain are not included.For supporting modeling of CPGs, works in [26, 27] defined linguistic patterns which are applied as a preprocessing step in the development of CPG models.Yang et al.[7]presented several treatment patterns and their modeling proposals (using BPMN, DMN or CMMN) in order to provide guidance in modeling the executable MTPs.Different from the linguistic patterns that are in text leval,the treatment patterns are process-oriented,frequently used in CPGs for all kinds of diseases.Although the treatment pattern based modeling can reduce the effort spent in modeling to some extent, all the process elements are modeled manually.This paper proposes an integrated MTP modeling approach that can generate the structured parent MTP models automatically.

III.MTP MODELING FRAMEWORK BASED ON PROCESS MINING AND TREATMENT PATTERNS

Hospital information systems record event logs by executing MTPs.If the MTPs conform to CPG specifications,business process mining algorithms can be directly performed on the logs to extract structured MTP models.However,they will not always output the appropriate MTP models that can be directly executed by workflow engines.Behaviors of time constraint activities, unstructured subprocesses, and diagnosis decisions cannot be extracted appropriately from logs using process mining algorithms but can be modeled by configuring treatment patterns [7].This section presents a semi-automatic MTP modeling approach that divides the modeling process into two stages: the first stage is to mine the structured parent MTP models from logs automatically,and the second stage is to model the subprocesses included in the parent models using treatment patterns as templates according to CPGs.Next, we introduce the MTP modeling approach framework at first.The details of the treatment patterns will be described in Section IV.

The integrated MTP modeling approach framework based on process mining and treatment patterns is shown in Figure 1.Given an event log of an MTP execution,an executable MTP model will be modeled with the following steps.Step 1: The subsequences and decision points conforming to treatment patterns are identified and represented with abstract activities.Specifically,the subsequences conforming to the time constraint patterns and the unstructured patterns are identified in each trace and replaced with abstract activities.The decision points conforming to the decision making patterns are identified and the decision abstract activities are inserted right there.Step 2:A process mining algorithm (e.g.SoFi) [28] is performed on the abstracted log to get a structured parent MTP model represented by BPMN.Step 3: The subprocesses represented by the abstract tasks in the parent model are modeled by configuring the corresponding treatment patterns using our implemented platform according to CPGs.They are invoked by the corresponding abstract tasks.Step 4: All data attributes processed by execution instances are added to the BPMN model as global variables to get the executable MTP model.

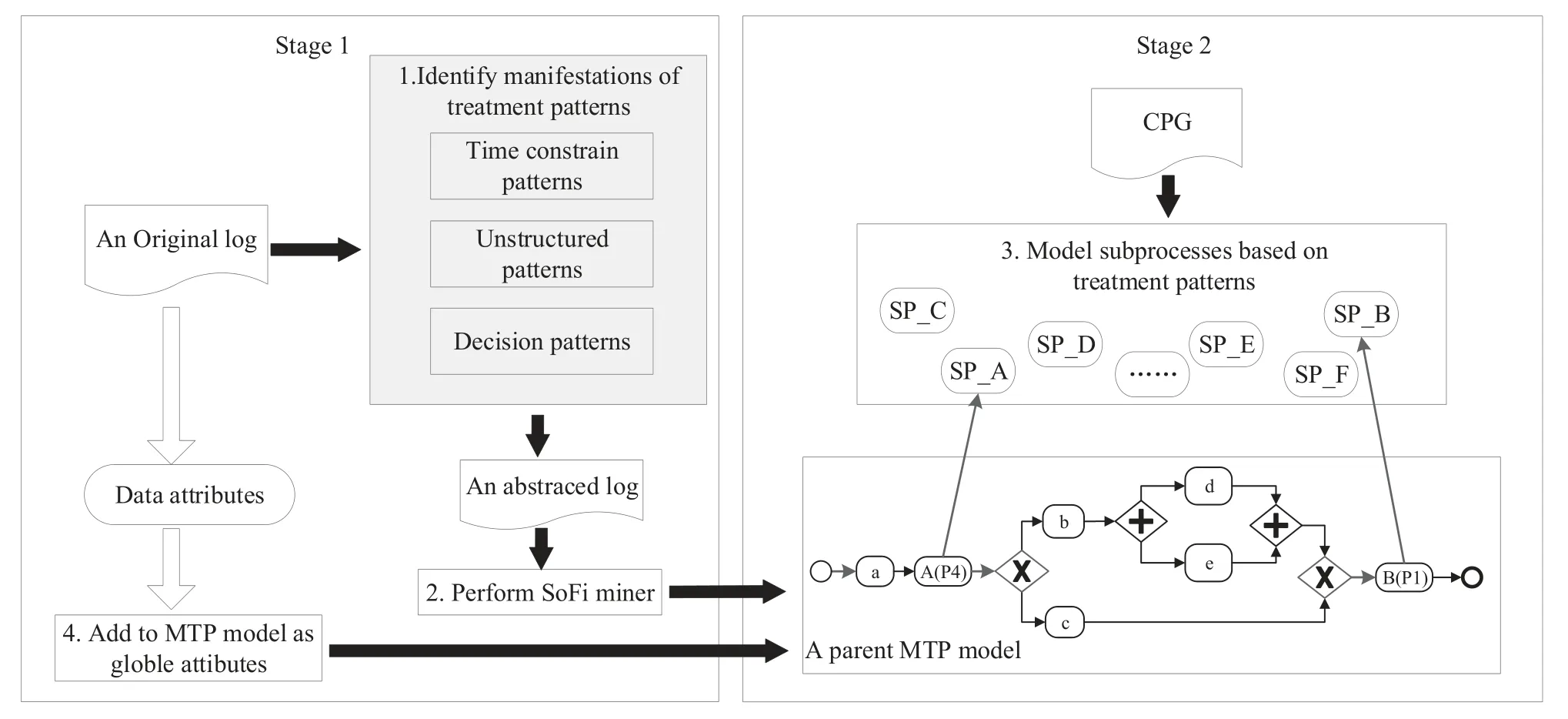
Figure 1. MTP modeling approach framework based on process mining and treatment patterns.

The order of pattern abstracting in Step 1 does not affect the processing result.The patterns of a category whose subsequences contain the most events in the log are usually abstracted first, because this will immediately reduce the log complexity largely in current processing.Based on the simplified log, the efficiency of abstracting other patterns will be improved.In addition, the identified subsequences or decision points conforming to the same patterns do not necessarily reflect the same behavior.Therefore, the processing in Step 1 not only identifies the subsequences conforming to the patterns, but also groups them by behavior type and determines the pattern type for each group.Subsequences in the same group are replaced by the same abstract activity.The processing not only identifies the decision points but also distinguishes their decision behavior types.The decision points with the same decision behaviors are inserted with the same decision abstract activity.SoFi algorithm [28] and the subprocess modeling with treatment patterns [7] are our previous work,so just steps in the shaded parts of the framework are described in the following sections.

IV.TREATMENT PATTERNS

In our approach framework, treatment patterns are used to capture their manifestations in logs at first,and subprocesses of these manifestations are modeled with the help of the generic models of these patterns later.We have extracted five treatment patterns[7]from 96 MTPs of different CPG documents, as listed in Table 1.These patterns are classified into three categories.Category I is used to describe activities with time constraints.Category II is used to describe unstructured process segments.Category III is used to describe diagnosis decision making logic.They are realized with process modeling languages, i.e.BPMN, DMN or CMMN.Each pattern represents different business behavior in medical domain.Some(all)of them may be contained in one MTP model, which depends on the specific business.Next,we introduce the treatment patterns and give some examples to explain them.

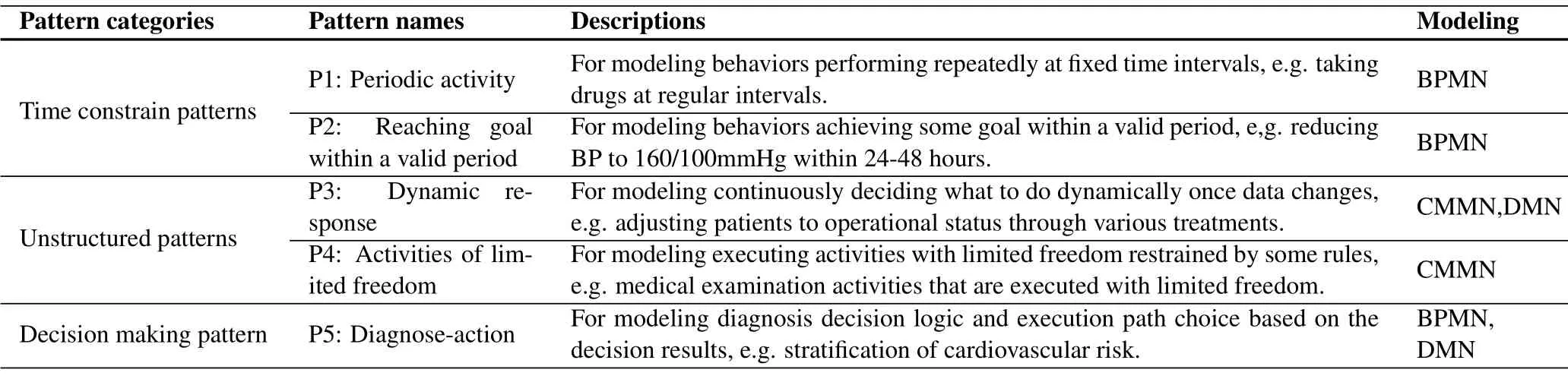
Table 1. Profiles of treatment patterns.

4.1 Time Constraint Patterns

Pattern P1 represents that an activity(or activities executed in sequence) is repeatedly performed at fixed time intervals.That will be interrupted by the expiration of time or interrupting conditions.

Definition 1.(P1: Periodic Activity) P1 =(Act,StartTime,TimeInterval,Interrupt Time,InterruptCondition),where Act is a sequential process of activities, StartTime is a timestamp when the Act starts at the first time, TimeInterval is a time interval between the occurrences of Act,InterruptingTime is a time duration the periodicactivity lasts,and InterruptingCondition is a set of conditions interrupting the execution of Act.

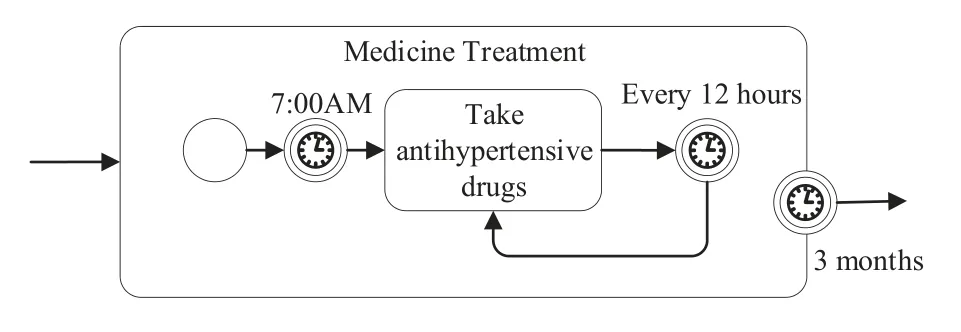
Figure 2. A medical treatment subprocess illustrating pattern P1.

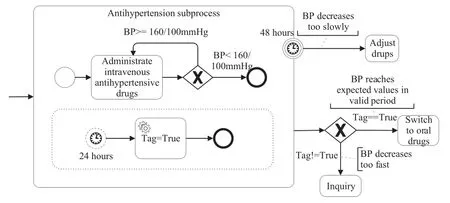
Figure 3. Antihypertension within a valid period illustrating pattern P2.

An instance of this pattern is illustrated by an expanded subprocess of BPMN, as shown in Figure 2.Task (also referred to an activity) “take antihypertensive drugs”is executed at a recent“7:00 AM”,and will be repeatedly executed at“every 12 hours”.The task will be interrupted after 3 months.Here, Act is configured as a single activity that is a special sequential process of just one activity.

Pattern P2 represents that an activity (or activities executed in sequence) is performed to achieve some goal within a valid period.

Definition 2.(P2: Reaching Goal within a Valid Period) P2 = (Act,GL,V alPeriod,Av,Af,As),where Act is a sequential process of activities.GL is a set of conditions that comprise a goal.V alPeriod=(EarlTime,LatTime)is a tuple where EarlTime and LateTime represent the earliest time and the latest time of a valid period respectively.Av is an activity executed when reaching the goal within the valid period.Af is an activity executed when reaching the goal before the earliest time.As is an activity executed when not reaching the goal within the valid period.

An instance of this pattern is illustrated by a subprocess of BPMN,as shown in Figure 3.Task“administrate intravenous antihypertensive drugs” is executedrepeatedly,the goal is“BP≤160/100mmHg”,and the valid period is 24 hours to 48 hours after“antihypertension subprocess”starts.If BP(Blood Pressure)reaches the goal within the valid period, the patient will switch to oral drugs.If BP decreases too fast,the patient should be inquired if he can tolerate this level of BP.If BP decreases too slowly,drugs are adjusted.

4.2 Unstructured Patterns

Pattern P3 represents that activities will be executed once patient data changes and meets the corresponding conditions.

Definition 3.(P3: Dynamic Response) Let C={c|c= (attr,op,val)} be a set of conditions, where attr is an attribute name,val is an attribute value and op is a relation operator.P3 = (AS,EC,F,Ru)is a tuple, where AS is a set of activities, EC is a set of entry criteria,F is a set of criterion associations,and Ru is a set of diagnosis rules.EC={ec|ec ⊆C},each entry criterion is a set of conditions.F ⊆(EC×AS)∪(AS×EC)is the set of associations that connect activities with entry criteria.The activity is executed once its entry criterion is specified to True.Let V={v|v=}be a set of attribute-value pairs.Ru={(Cond,OutP)|Cond ⊆C,OutP ⊆V}.If each condition in Cond of a rule is satisfied,then the rule is satisfied and the attribute in OutP is assigned the corresponding value.

An instance of this pattern is illustrated by aCase-PlanModel[18] of CMMN, as shown in Figure 4.It expresses the preparations for cataract surgery.Tasks of“application eye drops”,“loosening blockade”,“expanding with temporary implants”and“application of dilating liquids” are executed according to the output values of the task “evaluate patient status” (EPS) dynamically.EPS task invokes a DMN model of which a decision table realizes the diagnosis rules based on patient data.Each rule (also referred to each row in decision table) contains conditions and output of this rule.The decision results will be used to decide the next activity.The detailed decision table for this example is described in[7].

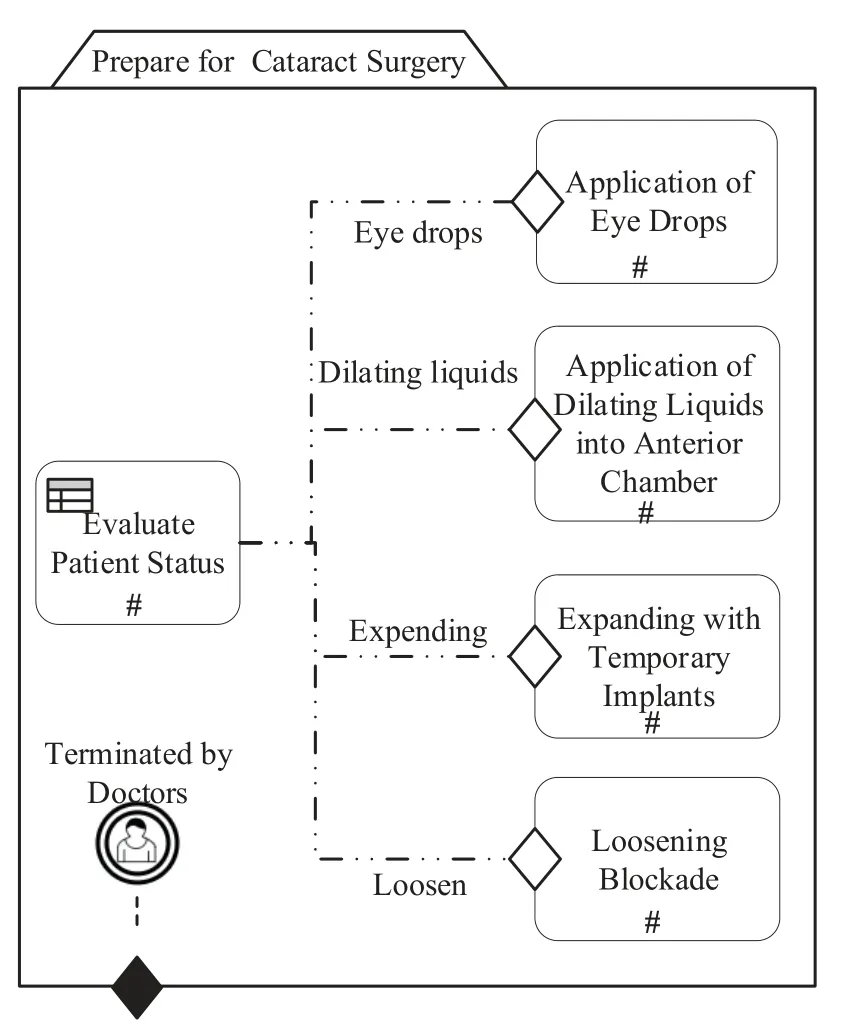
Figure 4. The preparations for cataract surgery illustrating pattern P3.

Pattern P4 represents that activities are executed with limited freedom restrained by rules in CPGs.

Definition 4.(P4: Activities of Limited Freedom)Let C={c|c=< attr,op,val >}be a set of conditions,P4=(AS,E,EC,F,αt)is a tuple,where AS is a set of activities,E is a set of directed edges,EC is a set of entry criteria, F is a set of criterion associations.E ⊆AS × AS is the set of edges connecting twoactivities which means an activity is executed after another.EC={ec|ec ⊆C} is a set of conditions.F ⊆(EC×AS)∪(AS×EC)is the set of associations that connect activities with entry criteria.αt:AS →{BasicActivity,ConditionedBasicActivity,Dis cretionaryBasicActivity,DiscretionaryActivity}associates each activity a specific type.Basic activitiesshould be performed on all patients,conditioned basic activitiesshould be performed with special entry criteria,discretionary basic activitiesshould be planned at points of care based on the outcome of preceding tasks,anddiscretionary activitiesshould be planned by doctors according to their experience.

An instance of this pattern is illustrated by aCase-PlanModelof CMMN, as shown in Figure 5.It expresses an unstructured process of several examination activities.Tasks of “blood biochemistry” and “complete blood count” (CBC) are basic items performed on all patients of suspected hypertension.Task“quantitative analysis of urinary albumin” is a conditioned basic item,compulsory for patients with diabetes mellitus.Task “postprandial sugar level test” is a discretionary basic item, planned based on the outcome of CBC (i.e.FBS >6.1mmol/L).Tasks of “TC”,“MRI”, “brain function” and “cardiac function” are discretionary items,planned according to the doctor’s individual experiences.

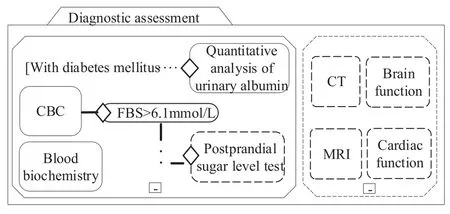
Figure 5.The unstructured examination process illustrating pattern P4.

4.3 Decision Making Patterns

Pattern P5 represents making diagnosis decisions and then determining which activities should be carried out next according to the decision results.

Definition 5.(P5: Diagnose-Action) Let C={c|c= (attr,op,val)} be a set of conditions, P5 =(Act,Cond,F,Ru) is a tuple consisting a set of activities Act, a power set of conditions Cond, a set of associations F, and a set of diagnosis rules Ru.Let Cond={cd|cd ⊆C},F ⊆(Cond×Act)∪(Act×Cond)is the set of associations that connect condition sets with activities.If each condition in a set is satisfied,the corresponding activity is executed.Ru is defined as the same as that in P3.

An instance of this pattern is illustrated by a BPMN model segment, as shown in Figure 6.Task “stratification of cardiovascular risk” (SCR) makes the diagnosis decision before reaching a gateway with three alternative paths.It invokes a DMN model of which a decision table realizes the diagnosis rules based on patient data.If each condition of a rule is satisfied,the rule is satisfied and the decision result contains the output of this rule.The decision results are labeled on the outgoing paths flowing into corresponding activities,thus determining the next treatment activities.Patients of“high or super high risk”results should be treated with medicine immediately, whereas patients of“medium or low risk”results monitor BP for one or three months respectively.The detailed DMN model of this example is described in[7].

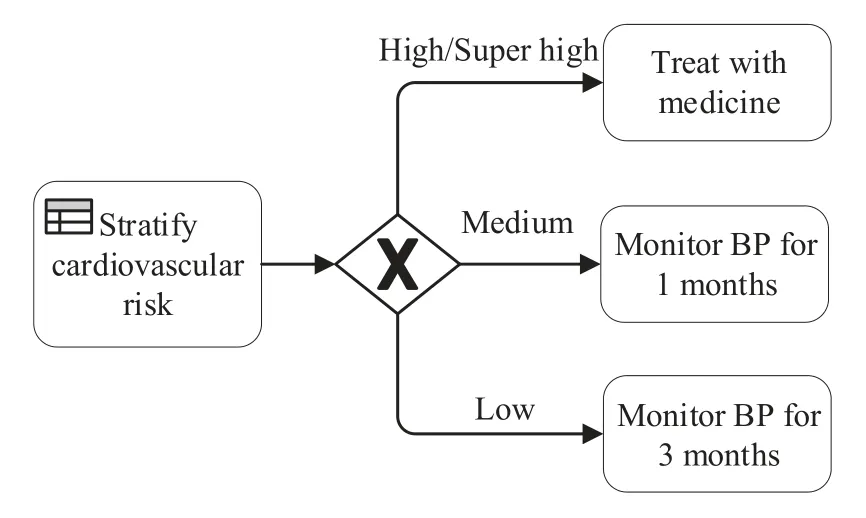
Figure 6. Stratification of cardiovascular risk illustrating pattern P5.

V.ABSTRACT MANIFESTATIONS OF TREATMENT PATTERNS

In our modeling framework, manifestations matching treatment patterns are captured and represented by abstract activities first.A process mining algorithm is then exploited on the abstracted log to obtain a structured parent MTP model.In this section, we introduce the abstracting methods in the order in which the experiment log is processed.Subsection 5.1 presents how to identify the manifestations of time constraints patterns,i.e.P1(Definition 1) and P2(Definition 2).Subsection 5.2 presents how to identify the manifestations of unstructured patterns, i.e.P3(Definition 3)and P4(Definition 4).Subsection 5.3 presents how to identify the decision points of the decision pattern,i.e.P5(Definition 5).The input of our framework is the execution logs of MTPs.Assume that it is possible to record events sequentially such that each medical event refers to a medical treatment activity and the occurring timestamp of the event.We first define the concepts of event,trace,and log.

Medical Event:LetAbe a finite set of treatment activities, andTthe time domain (set of timestamp primitives).A medical eventeis a paire= (a,t)wherea ∈Aandt ∈T.Formally, we usee.actande.time to denote the activity type, and the occurring timestamp of a medical eventerespectively.

Medical Trace:LetEbe the domain of medical events, a medical trace is a non-empty sequence of medical events, i.e.σ=〈e1,e2,...,en〉whereei ∈E(1≤i ≤n) is a particular medical event.The order of events inσusually respects the temporal order of their timestamps.We useσ(i,j)denotes the subsequence from theithposition to thejthposition in the traceσ,σ(i,j).actdenotes the activity sequence ofσ(i,j).

Medical Event Log:LetCbe the set of all possible medical traces.A medical event logLis a set of medical traces,i.e.L ⊆C.

5.1 Subsequences Conforming to Time Constraint Patterns

An activity sequence constituting a loop manifests itself in a tandem fashion in a trace,so the tandem arrays occurring in traces are first identified based on which subsequences conforming to time constraint patterns are further identified.

5.1.1 Identify Maximal Primitive Tandem Array

Tandem Array (TA):A tandem array in a traceσis a subsequenceσ(i,j) whose activity sequenceσ(i,j).actis the formαkwithk ≥2 whereαis a sequence of activities that is repeatedktimes.The activity sequenceαis called atandem repeat type.We denote a tandem array by the triple(i,α,k)where the first element corresponds to the starting position of the tandem array, the second element corresponds to the tandem repeat type,and the third element corresponds to the number of repetitions.

Maximal Tandem Array (MTA):A tandem arrayσ(i,α,k)in traceσis called a maximal tandem array if there are no additional copies ofαbefore or afterσ(i,α,k).

Primitive Tandem Repeat Type (PTRT):A tandem repeat typeαis called a primitive tandem repeat typeiff αis not a tandem array.

Maximal Primitive Tandem Array (MPTA):A maximal tandem arrayσ(i,α,k) is called a maximal primitive tandem arrayiff αis a primitive tandem repeat type.

Assume the traceσ=pqabcabcabcabcf.σ(3,abc,4),σ(3,abcabc,2) are both the MTAs.The corresponding tandem repeat types areabc,abcabcrespectively.The primitive tandem repeat type isabc.

5.1.2 Determine The Pattern Type

According to the definition of patterns,a subsequence that conforms to pattern P1 or P2 is an MPTA, and the pattern type depends on the time intervals between the activities.They can be represented formally as follows.

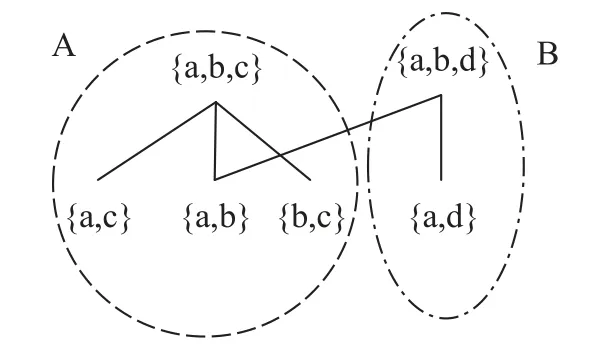
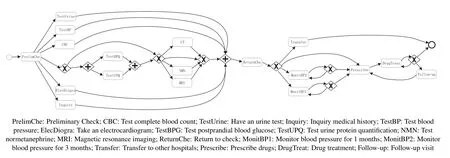
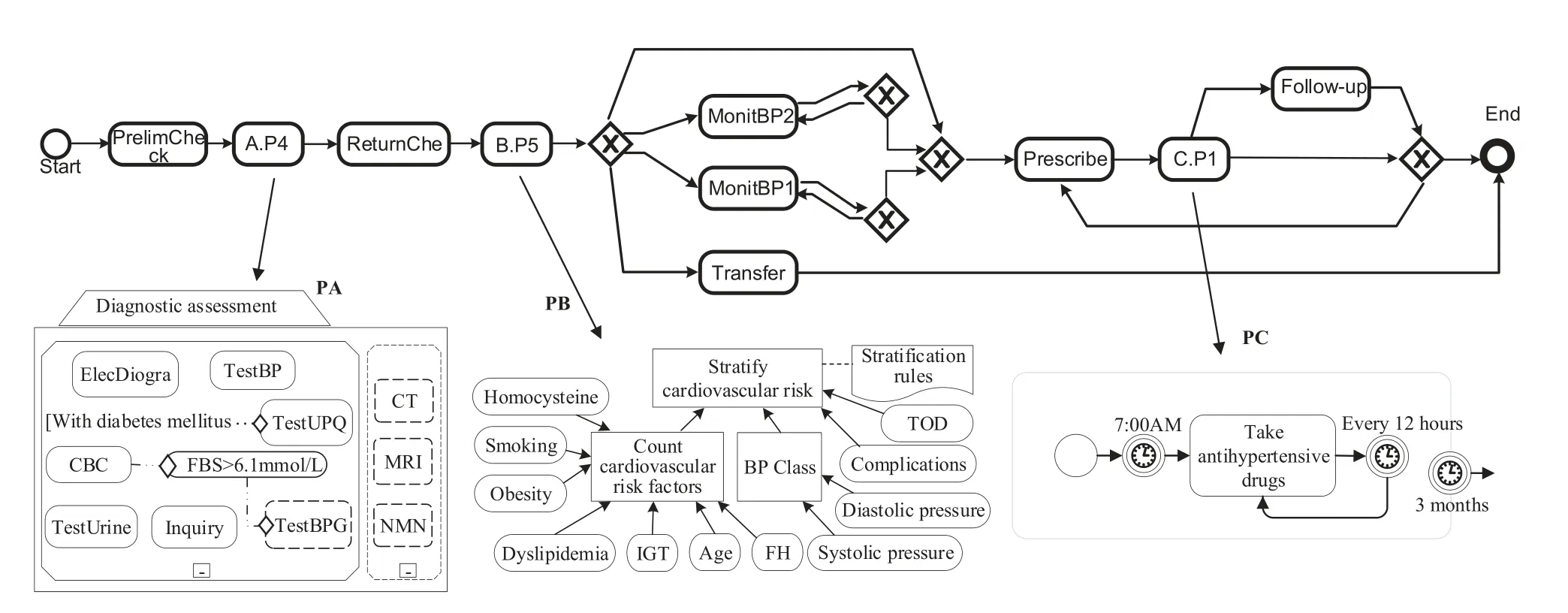
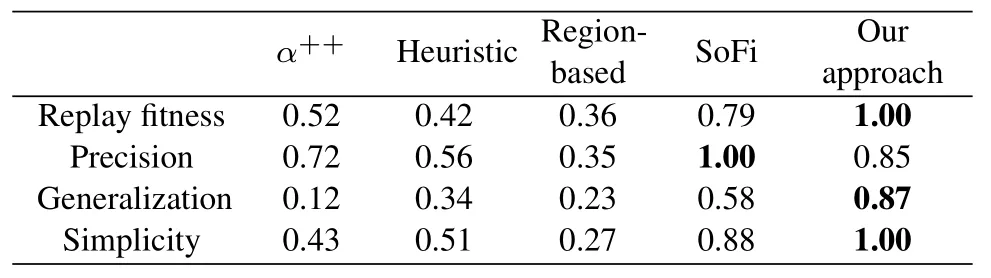
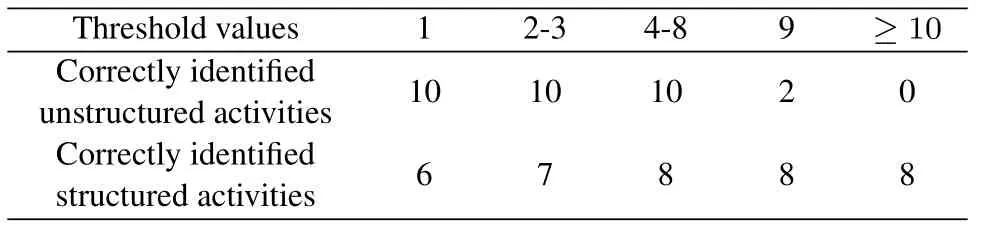
Subsequence of Pattern P1:Letσ(i,α,k) be an MPTA,σ(i,α,k)conforms to pattern P1,iff σ(i+p∗|α|).time−σ(i+(p−1)∗|α|).time=s(1≤p

Assume the traceσ=pqabcabcabcabcf,σ(3,abc,4) is an MPTA.Ifσ(3),σ(6),σ(9),σ(12)are performed at a fixed time intervals,σ(3,abc,4)conforms to pattern P1.

Subsequence of Pattern P2:Let [β] ={σ(i,α,k)| σ ∈L,α=β,σ(i,α,k) is an MPTA but doesn’t conform to P1}be the set of all MPTA with primitive tandem repeat typeβ.Let [β]•={σ(i+k∗|β|).act|σ(i,β,k)∈[β]}be the successors to [β].A subsequenceσ(i,α,k)∈[β] conforms to pattern P2,iff |[β]•|=3,and∀a,b ∈[β],a#Lb[8].

Algorithm 1. Identify subsequences of time constrain patterns.Input: L={c1,c2,...,cm}//ci is a medical trace Output:L′//Abstracted log 1: L′ = L;R = ∅;RType = ∅; //Initialize abstracted log L′, set of MPTA R, set of PTRT RType 2: for each trace c in L′ do 3: Identify all MPTA in c,Let R′ denote the set of MPTA,Let RType′ denote the set of PTRT 4: R=R ∪R′;RType=RType ∪RType′5: end for 6: Let B be a set of abstract activities.Define f :RType×{P1,P2}→B be the function that assigns to each PTRT of each pattern type an abstract activity.//Replace subsequences of pattern P1,P2 with abstract activities.7: for each trace c in L′ do 8: for each trace r in R do 9: if r.cid=c.cid then 10: j =r.i+r.k ∗|r.α|−1;11: if r has fixed time interval then 12: c.replace(r.i,j,f(r.α,P1));13: end if 14: if r hasn’t fixed time interval and|[r.α]•|=3 and ∀a,b ∈[r.α],a#Lb then 15: c.replace(r.i,j,f(r.α,P2));16: end if 17: end if 18: end for 19: end for 20: return L′

Subsequences with the same PTRT and pattern type can be considered as the same behavior,which are replaced by the same abstract activity in the log.The pseudo-code of the processing algorithm is shown in Algorithm 1.The input of this algorithm is the event logL,and the output is the abstracted logL′in which the subsequences of Pattern P1 and P2 are replaced.Line 2 to 5 gets the set of MPTA and the set of PTRT.A linear time algorithm [29] based on suffix trees is used to discover tandem repeats.In lines 7 to 15,the subsequences with the same PTRT that conform to pattern P1 are replaced with the same abstract activity.In lines 16 to 23, the subsequences with the same PTRT that conform to pattern P2 are replaced with the same abstract activity.Assuming that there areNtraces in the log and the number of MPTA isK,the time complexity isO(KN).

5.2 Subsequences Comforming to Unstructured Patterns

Unstructured subprocesses in an MTP tend to allow a large degree of flexibility: it is left to physicians to decide when or whether to execute a medical activity according to patient individual conditions as long as they don’t violate clinical rules.In an MTP model,such subprocesses are suitable contained in separate subprocesses modeled with our unstructured treatment patterns.This subsection continues to process the subsequences conforming to the unstructured patterns to further simplify the log.Firstly,we use a context analyze technique[30]to distinguish an activity as structured (occurring in a structured subprocess) or unstructured (occurring in an unstructured subprocess).This is based on the number of predecessors and successors that the activity has.Then, the unstructured subsequences consisting of successive events with unstructured activities are extracted.Next, find the abstractions of the unstructured subsequences and determine the pattern types of them.Finally, unstructured subsequences with the same abstraction and pattern type are replaced with the same abstract activity.

5.2.1 Identify Unstructured Subsequences

LetAbe a finite set of treatment activities,L={c|c=< e1e2...en >}be a medical event log, we define the predecessors and successors of an activitya ∈Aas follows.

Predecessors:∀a ∈A, a set of activities executed directly precedingais the predecessors ofa,denoted as•a={ei−1.act|ei.act=a,〈ei−1ei〉is the subsequence ofc,2≤i ≤|c|,∀c ∈L}.

Successors:∀a ∈A, a set of activities executed directly behindais the successors ofa, denoted asa•={ei+1.act|ei.act=a,〈eiei+1〉is the subsequence ofc,1≤i<|c|,∀c ∈L}.

We consider an activity to be unstructured when it has a large number (bigger than a threshold) of both predecessors and successors.An activity with a small number of predecessors or a small number of successors is considered to be structured.The reasoning behind these cases is as follows: if an activity has a high number of predecessors and a high number of successors,there are few rules constraining when exactly the activity can occur.We then consider it likely to fit well into an unstructured subprocess.Similarly, if an activity has only a small number of predecessors and a small number of successors,it is probably more easily modeled procedurally,for example,as a sequence or a choice from a low number of options.In the case that an activity has a small number of predecessors, but a large number of successors, we consider it likely that the activity is either the last element in a structured part of process, which is followed by an unstructured part of process, or that the activity is followed by a choice from a large number of options.In both cases it makes sense to consider this as a structured activity.Similarly, in the case that an activity has a small number of successors,but a large number of predecessors we consider it likely that the activity is either the first element in a structured part of process,which was preceded by an unstructured part of process, or that the activity joins a choice from a large number of options.In both cases it seems fitting to consider this as a structured activity.

5.2.2 Find Abstactions of Unstructured Subsequences

Unstructured subsequences are extracted by combining successive events associating to unstructured activities.All the unstructured subsequences compose an unstructured log.Different unstructured sequences sharing the same or similar activity set may be generated from the common unstructured subprocess.In this subsection,we propose the concept of abstraction to identify unstructured subsequences of the common unstructured subprocess.

Subsequence Alphabet:LetL′be the set of unstructured subsequences,σ ∈L′,subsequence alphabet Γ(σ)is the set of activities that appear inσ.

Assuming there are three unstructured subsequences of events whose activity sequences are〈acca〉,〈apqef〉,〈apeqf〉, the corresponding subsequence alphabets are{a,c},{a,e,f,p,q},{a,e,f,p,q}respectively.Different unstructured subsequences can share a common alphabet.In this example,subsequences〈apqef〉and〈apeqf〉share the same alphabet{a,e,f,p,q}.

Unstructured subsequence abstractions can be discovered by considering a partial ordering on the subsequence alphabets.Subsumption is used as the cover relation.A subsequence alphabetσ1covers another alphabetσ2ifσ2⊆σ1.Consider two unstructured subsequences of events whose activity sequences are〈abcd〉and〈acd〉.It is most likely that they pertain to a common unstructured subprocess, because they capture the variations of an unstructured subprocess execution, i.e.bis not executed in the second subsequence.Therefore, by defining a partial order on the subsequence alphabets and generating a Hasse diagram, one can form abstractions by considering the maximal elements in the poset.

Unstructured Subsequence Abstraction:LetL′be the set of unstructured subsequences,σ ∈L′,Γ(σ)be the subsequence alphabet onσ,[X] ={σ|Γ(σ) =X,σ ∈L′}be the set of unstructured subsequences sharing a common subsequence alphabetX.LetP={X|X= Γ(σ),σ ∈L′}be the set of subsequence alphabets onL′,be the poset onP,,Zis the abstraction of[X].Zis the maximal element on.

A partial ordering on the subsequence alphabets is depicted as a Hasse diagram, as shown in Figure 7.{a,b,c}and{a,b,d}are two maximal elements of the partial ordering.Let us denote these two maximal elements (also referred as abstractions) with abstract activitiesAandBrespectively.Alphabets that contribute to more than one maximal element can be put in one of the maximal elements.Let us assume that the alphabet{a,b}is assigned to the maximal element{a,b,c}.With this abstraction,all unstructured subsequences with alphabets{a,b},{b,c},{a,c}and{a,b,c}are represented by abstract activityA, while the unstructured subsequences with alphabets{a,d}and{a,b,d}are represented by abstract activityB.

If an abstraction doesn’t cover any subsequence alphabet in a Hasse diagram,the subsequences with the abstraction could be the observations of a concurrent structure.They can be regarded as the observations of a concurrent structure if there are enough different activity subsequences,because they can be mined automatically.Assuming there are N activities in a concurrent subprocess,at leastN(N−1)different activity sequences are needed to mine the concurrent structure[28].Therefore,if there are more thanN(N −1)different activity subsequences,the subsequences are regarded as the observation of a concurrent structure.

Figure 7. A hasse diagram over unstructured subsequence alphabets.

Figure 8. Three MTP models by performing classic process mining algorithms on the original log.

5.2.3 Determine The Pattern Type

Next, we determine the pattern type for the unstructured subsequences sharing the common abstraction.

Subsequence of Pattern P3:LetL′be the set of unstructured subsequences,be the poset of subsequence alphabets,Zbe the maximal element on, Let [[Z]] ={σ|Γ(σ) =be the set of unstructured subsequences sharing a common abstractionZ.[[Z]] conforms to pattern P3iff ∀r ∈[Z],there are repetitive activities occurring inr.

Subsequence of Pattern P4:LetL′be the set of unstructured subsequences,be the poset of subsequence alphabets,Zbe the maximal element on, Let [[Z]] ={σ|Γ(σ) =be the set of unstructured subsequences sharing a common abstractionZ.[[Z]] conforms to pattern P4iif ∀r ∈[Z],there are no repetitive activities occurring inr.

Unstructured subsequences with the same abstraction and pattern type can be considered as the same behavior,which are replaced by the same abstract activity in the log.The pseudo-code of the processing algorithm is shown in Algorithm 2.The input of this algorithm is the event log LandL′including unstructured subsequences extracted fromL.The output of this algorithm is the abstracted logL′′′in which the subsequences of unstructured patterns are replaced.Line 2 to 6 gets the set of abstractions inL′.For each abstraction,all the subsequences of the same abstraction are divided into the same group in lines 9 to 14.Line 15 to 17 excludes the concurrent subsequences.The pattern type of the subsequences is determined in lines 18 to 24.In lines 25 to 29,the subsequences with the same abstraction and pattern type are replaced with the same abstract activity.Assuming that there areNsequences inL,Msequences inL′, and the number of abstractions isK,the time complexity of the algorithm isO(K(M+N)).

Algorithm 2. Identify subsequences of unstructured patterns.Input: L = {c1,c2,...,cm},L′ = {c′1,c′2,...,c′n}Output:Abstracted log L′′′1: L′′′ = L;AB = ∅; //Initialize L′′′ and the set of unstructured alphabets AB 2: Get the set of unstructured alphabets AB on L′;Find maximal elements MaxAB on AB 3: Let C be a set of abstract activities.Define f :MaxAB ×{P3,P4} →C denote the function that assigns to each abstraction of each pattern type an abstract activity;4: for each trace M in MaxAB do 5: L′′ =∅;6: for each trace c′ in L′ do 7: if the alphabet of c′ is subsumed by M then 8: L′′ =L′′∪{c′};//Put subsequences of the same abstraction in L′′9: end if 10: end for 11: if L′′ has enough different sequences and M doesn’t cover any subsequence alphabet then 12: Exit for;13: end if 14: for each trace c in L′′′ do 15: if there exits trace θ in L′′ and θ has multiple activity and i=c.find(θ)>0 then 16: c.Replace(i,i+|θ|−1,f(M,P3));17: Exit for;18: end if 19: c.Replace(i,i+|θ|−1,f(M,P4));20: end for 21: end for 22: return L′′′

5.3 Decisions Conforming to Decision Making Patterns

The diagnosis decision process within an MTP cannot be extracted from the log using process mining algorithms,because the decision process does not leave a trace in the log.According to the modeling guidance of the decision making pattern (i.e.pattern P5),a diagnosis decision subprocess realized with a DMN model is invoked by a single decision activity in the structured parent MTP model.Therefore, we want to identify the decision points in traces, and insert decision abstract activities right there, i.e.leave decision impresses in the log.Performing a process mining algorithm on the processed log, the abstract tasks in the MTP model represent decision subprocesses which will be modeled by configuring the decision making pattern later.In this subsection, we continue to exposes the approach to identify the decision points conforming to pattern P5.

Algorithm 3. Identify decisions of decision making patterns.Input: L={c1,c2,...,cm}Output:L′//Abstracted log 1: L′ =L;D =∅;//Initialize L′ and the set of decision types D 2: for each trace c in L′ do 3: Identify the decision points in c, let d(c,i) denote a decision point in c,let ei denote the event in front of d(c,i).4: D =D ∪{(ei.act)•};5: end for 6: D is clustered by similarity of the elements,let D be the clusters of decision type.7: Let D denote a set of abstract activities.Define f : D →D be the function that assigns to each decision type cluster an abstract activity.8: for each D in D do 9: for each trace c ∈L′ do 10: if there exists a decision point d(c,i)in c and the decision is complex then 11: c.insert(i,f(D));12: end if 13: end for 14: end for 15: return L′

5.3.1 Identify Decision Points

An activity with some successors is possibly followed by a choice if there are not any direct succession relations between these successors.We define the position following an event as a decision point.

Decision Point:LetL={c1,c2,...,cn}(n ∈N)be an event log,eibe an event in a traceck,ck ∈L.ais the activity ofei, i.e.ei.act=a.Letθbe the threshold use for unstructured subsequences.The position subsequently behind the eventeiis a decision pointiff |•a| ≤θ,∀s,t ∈a•,s#Lt, denoted asdec(ck,i).

5.3.2 Determine The Decision Behavior Type

Decision points of the same decision behavior will be inserted with the same decision abstract activity.Letdec(c,i)be a decision point in tracec,eibe the event in front of the point, the decision behavior type ofdec(c,i) depends on the successors ofei.act.Decision points with the same or similar decision type entail the same decision behavior.The similarity of decision type can be defined in multiple ways.LetX,Ybe the decision types of two decision points.They are considered to be similar provided they share a set of common elements above a particular threshold and also when the difference between them is less than another threshold.In other words,Xis similar withYif|X ∩Y| ≥δs,|(X −Y)∪(Y −X)| ≤δd.δscorresponds to the threshold on the number of common elements,whileδdcorresponds to the threshold on the number of differences betweenXandY.They can either be a fixed constant or a fraction of the cardinality of the decision type elements.The decision types are clustered according to the similarity.Decision types in the same cluster represent the same decision behavior.

5.3.3 Determine The Pattern Type

Decisions in MTPs cannot necessarily be modeled using Diagnose-Action pattern (i.e.pattern P5).Only the complex decision related to business rules(e.g.diagnosis rules)should be modeled with pattern P5.The decision abstract activities should be inserted at the decision points entailing complex decisions.

Decision of Pattern P5:LetL={c1,c2,...,cn}(n ∈ N) be an event log,Dthe set of decision points with the same decision behavior type.The decision point inDconforms to pattern P5iffthere exists a complex decision at the point.

The complex decision can be determined in multiple ways.LetLbe an event log,Dbe a set of decision points with the same decision behavior type.For each decision pointdec(c,i)∈D,c ∈L,leteibe the event in front of the point,letATTR(ei)be the data properties at the eventei.Next,ATTR(ei)is considered as an input of the decision,ei+1.actis considered as a result of the decision.Based on all the inputs and results of decision points inD, a machine learning method can be used to determine the complexity of the decision.If a decision tree is constructed based on the data properties and results, the deeper the decision tree is,the more complex the decision is.

The decision points conforming to pattern P5 with the same decision type are inserted with the same decision abstract activity.The pseudo-code of processing algorithm is shown in Algorithm 3.The input of this algorithm is the event logL.The output of this algorithm is the logL′in which the decision abstract activities are inserted.Line 2 to 5 identifies the decision points inLand gets a set of decision types.In lines 8 to 14,decision abstract activities are inserted at the decision point if the decision is complex.Assuming that there areNtraces in the logLand the average length of each trace isM,then the time complexity of the algorithm isO(MN).

VI.EVALUATION

The evaluation is separated into two parts.First, we implement the log processing approach in java and conduct three experiments on a synthetic log of nonsecondary hypertension MTP described in Chinese hypertension CPGs [31].Then, we gather the feedback from physicians in a Shanghai hospital to analyze the conformance between behaviors expressed by the resulted MTP model and the corresponding expressions described in Chinese hypertension CPGs [31].This MTP includes behaviors conforming to three types of patterns described in Section IV.We compare the MTP models generated by process mining approaches on the original log with that generated by the modeling approach proposed in this paper.The selected process mining algorithms areα++[32], Heuristic [10],Region-based[33]and SoFi[28].Theα++algorithm is able to adequately deal with non-free-choice behavior.Heuristic algorithm takes into account the frequency of a relation, so it is robust to noise.Regionbased algorithm aims at producing a process model that is similar to a transition system.Each algorithm has its own pros and cons.SoFi is an integrated approach based on genetic algorithm (GA), which integrates the advantages of the three algorithms.We apply the ProM to perform these algorithms on the log and transform the resulted models of different algorithms into BPMN representation.These models are compared specifically with respect to the understandability and the quality criteria[8]in terms of replay fitness,precision,generalization and simplicity as well.

6.1 Experiments and Results Analysis

6.1.1 Design of Experiments

We create a set of BPMN models of the non-secondary hypertension MTP with Camunda modeler[23].Each one contains one of the variations of the unstructured process segment in it.PLG (Process Log Generator)tool [34] is applied to generate a log on each of the models.All the logs are gathered to form the synthetic log of the non-secondary hypertension MTP, which contains 5000 instances, 67106 events in all.It can be downloaded from Github .Next, we applyα++,Heuristic,Region-based,SoFi and our proposed modeling approach to produce MTP models respectively.We design the experiments as follows.

(1) We performα++,Heuristic and Region-based algorithms on the original log respectively to produce three MTP models.

(2) We directly utilize the integrated mining approach SoFi to produce an MTP model.The original log is divided into three sublogs according to the cardiovascular risk.Three algorithms in the 1st experiment are used to prepare the initial population.For overall fitness measurement in SoFi,the weight coefficients on four quality dimensions[8]i.e.replay fitness,precise,generalization and simplicity are 0.3, 0.3, 0.1, and 0.3.The mutation and crossover rates are 0.1 and 0.5.The mining process ends when reaching maximum number of generations as 1000.

(3) We utilize our proposed modeling approach to generate a MTP model.SoFi miner is performed on the abstracted log to produce a structured parent MTP model.The subprocesses represented by abstract tasks in the parent model are modeled with the corresponding treatment patterns in accordance with CPGs and are invoked by the abstract tasks.Parameter settings are the same as those in the 2nd experiment.

6.1.2 Experimental Result Analysis

Three models of the 1st experiment are like spaghettilike shapes, shown in Figure 8.They are too complicated to understand and cannot be used in practice obviously.This is due to the medical examination subprocess in the MTP.Examinations in this subprocess can be performed in almost any order just restrained by some rules.Three algorithms applied in the 1st experiment can’t deal with the flexibility of the unstructured subprocess.The resulted model of the 2nd experiment is shown in Figure 9,which is much simpler than those in the 1st experiment.However, the resulted model does not contain all the compliant medical behaviors in the log, i.e.some behaviors in the log are not expressed in the model,because the SoFi miner still cannot deal with the unstructured subprocess well.In addition, the decision process after examinations is not contained in the model, because the SoFi miner cannot deal with complicated decision logic.The resulted model of the 3rd experiment is shown in Figure 10.The abstract tasks are represented by capital letters and pattern names labeled in it.“A.P4”means that the subprocess represented by the abstract task A conforms to pattern P4.The subprocesses represented by abstract tasks in the parent model are modeled with the corresponding treatment patterns in accordance with CPGs.PA is a subprocess model of diagnostic assessment,PB is a subprocess model of cardiovascular risk stratification,and PC is a subprocess model of drug treatment.These subprocesses are invoked by the corresponding abstract activities(such as PA,PB)or embedded in the parent model (such as PC).The subprocess PA contains all the compliant examination behaviors in the log, and the subprocess PB expresses the diagnosis decision logic.In addition, the modular structure of the model to some extent helps to understand the MTP more easily.

Next,we calculate the quality of the models in terms of replay fitness, precision, generalization and simplicity.The values are shown in Table 2,ranging from 1 (best) to 0 (worse).As can be seen, the replay fitness values of the MTP models generated in the 1st and 2nd experiments range from 0.36 for the Regionbased miner to 0.79 for the SoFi miner, which means that some traces in the log cannot be replayed by the mined process models.This is because these four process mining algorithms cannot deal with the unstructured subprocess well.The replay fitness value of the MTP model generated by our approach in the 3rd experiment equals to 1,which means all the traces in the log can be replayed by the mined process model.This is because the unstructured subprocess in the model is modeled with our proposed unstructured pattern (i.e.Pattern P4), thus the model contains all the compliant behaviors in the log.The precision value of the MTP model generated by our approach equals to 0.85,just lower than that(equals to 1.00)generated by SoFi miner.Although we create the variations of the unstructured process segment as many as possible for generating the log,not all the compliant behaviors are included in the log.Therefore,some traces in compliance with the model in Figure 10 are not in the log,so the precision value of this model is less than 1.00.A model with high precision may be overfitting,which is related to generalization criterion.The generalization value(equals to 0.87)of the model in Figure 10 is the best.It indicates that the discovered model can generalize the behavior seen in the log more appropriately,so that it will be less possible to be invalidated by the next set of observations than those discovered by the other four algorithms.Therefore, the process mining in our approach framework can automatically generate more accurate MTP model, and the subprocess models based on treatment patterns make the model easy to understand.

Figure 9. Non-secondary hypertension MTP model by performing SoFi miner on the original log.

Figure 10. Non-secondary hypertension MTP model using the proposed modeling approach.

Table 2. Values of three criteria for the generated parent models.

6.1.3 Parameter Analysis

In the modeling framework, an activity is considered to be unstructured when it has a large number(larger than a thresholdθ) of both predecessors and successors.To analyze the effect of the threshold values on the identification result, we test the threshold values from 1 to 10 in the 3rd experiment.There are altogether 18 medical activities in the experimental log.They are exhibited as the atomic task in Figure 9.Among them, ten activities are unstructured and eight activities are structured.The identification results for different threshold values are shown in Table 3.All the activities are correctly identified if the thresholdθis set from 4 to 8.If the threshold is set very large, such asθ ≥10, all the structured activities are correctly identified, but all the unstructured activities are treated as structured, because the minimum number of the predecessors or successors of an unstructured activity is no more than ten.When the threshold is set as 9,two out of ten unstructured activities are treated as structured, because they have nine predecessors or successors.If the threshold is set very small,all the unstructured activities are correctly identified,but some structured activities may be treated as unstructured.In the experiment, when thresholdθis set as 2 or 3, one structured activity is treated as unstructured.It has ten predecessors and four successors.Actually, it is followed by a choice from four options.Although this does not influence the resulted model too much,it is better explained as structured to result in a more precise model.Ifθis set as 1,another structured activity is also treated as unstructured.It actually has two predecessors and successors.Therefore,the threshold in the 3rd experiment is eventually set as 4.

Table 3. Identified activities for different threshold values.

6.2 Empirical Findings

To gather empirical evidence supporting the effectiveness of our proposed approach, we analyze the conformance between behaviors expressed by the resulted non-secondary hypertension MTP model and the corresponding expressions described in Chinese hypertension CPGs [31].We interviewed 26 physicians working in the cardiology or geriatrics department in Putuo hospital affiliated to Shanghai University of Traditional Chinese Medicine, and explained the behaviors expressed by this MTP model to them.CPGs have been implemented in this hospital for several years.The profiles of these physicians are listed in Table 4.Then,they were asked to answer a questionnaire.The questionnaire was designed to subjectively evaluate the MTP model according to two measures:CorrectnessandCompleteness.Questions designed for both measures are listed in Table 5.They were defined on four-point Likert scales,from 1(completely disagree)to 4(completely agree).

Table 4. Profiles of the interviewed physicians.

Table 5. Questionnaire for evaluating the resulted MTP models.

We calculated the percentage frequencies of responses for all options on the questions.100% interviewed physicians considered that no behaviors expressed by the MTP model violate the expressions described in Chinese hypertension CPG (Correctness).76.9%physicians answered“completely agree”on the question of completeness.23.1% physicians answering“generally agree”on this question considered that contents in the Chinese hypertension CPGs are more comprehensive,for instance,the detailed drug instructions and the interpretations of professional terms are included.However, because this kind of content is not process-related, we consider they needn’t be expressed in the MTP model.Findings from the feedbacks show that the behaviors expressed in the resulted MTP model are in accordance with the expressions described in CPGs.

VII.CONCLUSIONS

This paper presents an integrated MTP modeling approach framework based on process mining and treatment patterns.It divides the modeling process into two stages:the first stage is to mine structured parent MTP models from abstracted logs automatically, and the second stage is to model subprocesses included in the parent models using treatment patterns as templates in accordance with CPGs.In this framework, we propose a log processing approach to identify the manifestations of the three types of treatment patterns and represent them with abstract activities.The proposed approach integrates the advantages of process mining and treatment pattern based modeling,taking both ef-ficiency and quality into account.The process mining in our approach framework can generate more accurate parent MTP models from abstracted logs.The subprocess models based on treatment patterns make the MTP models easy to understand.

ACKNOWLEDGEMENT

The work is supported by Chinese National Key Research and Development Program (No.2017YFB1400604).

The authors are thankful for the positive support received from the Putuo hospital affiliated to Shanghai University of Traditional Chinese Medicine as well as to all medical staff involved.