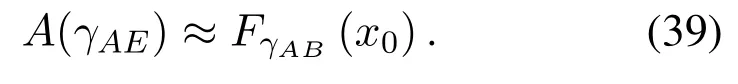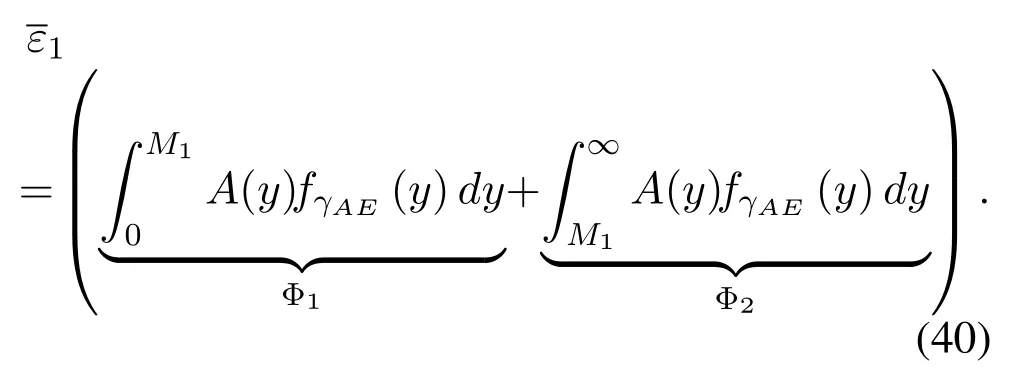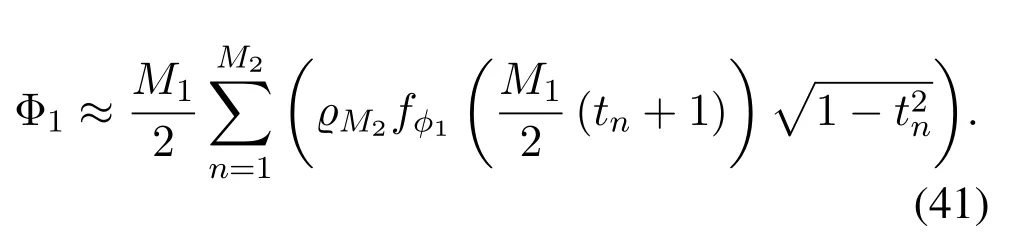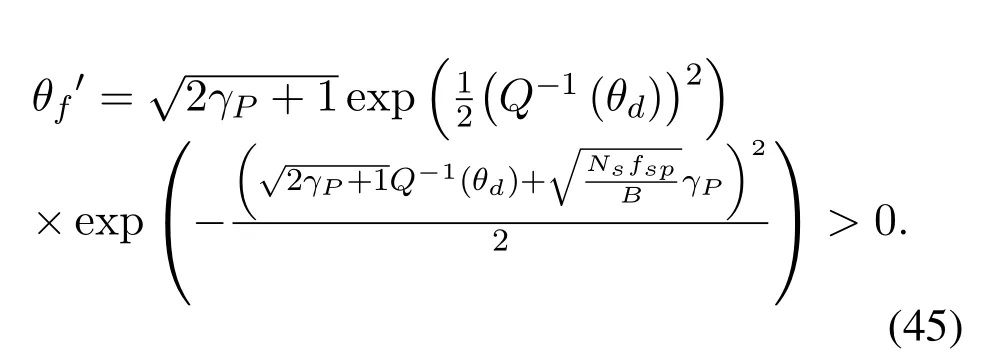Relay-Assisted Secure Short-Packet Transmission in Cognitive IoT with Spectrum Sensing
Yong Chen,Yu Zhang,,*,Baoquan Yu,Tao Zhang,Yueming Cai
1 College of Communication Engineering,Army Engineering University of PLA,Nanjing 210007,China
2 The Sixty-third Research Institute,National University of Defense Technology,Nanjing 210007,China
Abstract: Cognitive Internet of Things(IoT)has attracted much attention due to its high spectrum utilization.However, potential security of the shortpacket communications in cognitive IoT becomes an important issue.This paper proposes a relay-assisted maximum ratio combining/zero forcing beamforming(MRC/ZFB) scheme to guarantee the secrecy performance of dual-hop short-packet communications in cognitive IoT.This paper analyzes the average secrecy throughput of the system and further investigates two asymptotic scenarios with the high signal-to-noise ratio (SNR) regime and the infinite blocklength.In addition, the Fibonacci-based alternating optimization method is adopted to jointly optimize the spectrum sensing blocklength and transmission blocklength to maximize the average secrecy throughput.The numerical results verify the impact of the system parameters on the tradeoff between the spectrum sensing blocklength and transmission blocklength under a secrecy constraint.It is shown that the proposed scheme achieves better secrecy performance than other benchmark schemes.
Keywords:cognitive Internet of Things;short-packet communications; physical layer security; spectrum sensing
I.INTRODUCTION
1.1 Background
The Internet of things (IoT) extends the communication from the service for people to the service for devices [1, 2].Vast IoT applications introduce massive data into the network,which requires massive wireless spectrum resources.However,there is very little special spectrum allocated to IoT devices due to scarcity of spectrum resources.Fortunately,the application of cognitive IoT can greatly reduce the demand for spectrum resources[3].
However, the communication security problem in IoT is gradually exposed when people enjoy the services of cognitive IoT.Some critical IoT applications,such as cloud monitoring and unmanned combat e often subject to illegal eavesdropping and attacks [4].The traditional secure communication based encryption algorithms is not suitable for cognitive IoT.This is because these devices in cognitive IoT are limited by their computing power, storage space, and battery power.Complex encryption methods are not friendly to these IoT devices [5].Therefore, it is necessary to design a lightweight security mechanism to support the cognitive IoT.It should be noted that, physical layer security exploits the random nature of wireless channels to ensure communication security, and can avoid complex secret key generation,distribution,and management.This just meets the security and lightweight requirements of critical IoT applications,so it is necessary to study the physical layer security in the cognitive IoT[6,7].
Most existing works about physical layer security assume the packets are long,and the Shannon formula can be adopted to analyze the secrecy performance.However, the data gathering, inference and control transmitted by these devices in cognitive IoT is usually very short[8].In this case,the information transmission is more likely to interrupted or leaked,the traditional physical layer security scheme has limitations in short-packet communications, so it is necessary to study new secrecy schemes for short-packet communications[9].Correspondingly,short-packet theory is exploited to analyze and optimize the secrecy performance in this paper[10].
1.2 Related Work
Considering the limited hardware and significant energy constraints in cognitive IoT,we can use relays to expand coverage and assist secure transmission.Some existing works investigated the relay-assisted secure transmission scheme in the cognitive network.The work in[11]derived the closed-from expression of the secrecy outage probability for a dual-hop multiantenna cognitive system.Fan et al.studied a secure switch and stay combining protocol in a relay-assisted underlay cognitive network, and analyzed the secrecy outage probability of the system[12].The authors in[13]evaluated the secrecy performance of a cognitive relay system with multiple eavesdroppers, and derived the closed-form expression of the achievable secrecy rate.In addition, Wang et al proposed a secure transmission scheme for an energy harvesting based cognitive multi-relay network[14].
However, the above works adopted the Shannon formula to investigate the secure transmission performance.Considering the short-packet characteristic of IoT, it is necessary to investigate the secure shortpacket communications.In [15], the authors investigated the secrecy capacity under the constraints of secrecy,error probability,and information leakage from the information theory point of view.In practice, the secrecy capacity cannot be guaranteed successfully and securely, thus optimizing secrecy throughput is more important in this sense.The authors in[16,17]investigated the secrecy throughput in the IoT, and proposed secrecy performance analysis frameworks from the condition taht the channel state information available or unavailable, respectively.Furthermore,non-orthogonal multiple access (NOMA) and uplink massive multiple-input-multiple-output(MIMO)technologies have been applied in IoT to ensure the secure transmission of information,e.g.,[18–20],in response to different communication requirements.
Nevertheless, the above secrecy schemes are difficult to be directly applied in cognitive IoT.For the secure communication in the cognitive IoT, whether the IoT devices can accurately sense the channel occupation not only affects the degree of interference to the primary user, but also affects the secrecy performance in cognitive IoT.When the transmission packet is short, the sensing blocklength cannot be neglected,and the perfect sensing assumption is not realistic[21].In this case, the sensing blocklength has a significant impact on the communication performance of the IoT devices, and the traditional secrecy performance optimization method based on perfect sensing assumption is not applicable.Hence, it is essential to design new schemes for secure short-packet communications in cognitive IoT.
1.3 Motivation and Contribution
Based on the above analysis, this paper investigates relay-assisted secure short-packet communications in cognitive IoT with spectrum sensing.Considering the impact of spectrum sensing time and decoding error probability on system security,the secrecy throughput is thoroughly analyzed and optimized.The contributions of this paper are described as follows:
• This paper designs a relay-assisted secure transmission scheme, named maximum ratio combining/zero forcing beamforming (MRC/ZFB), for short-packet communications in cognitive IoT.The closed-form approximation for the secrecy throughput is derived.
• The tradeoff between the spectrum sensing blocklength and transmission blocklength under a secrecy constraint is analyzed.In particular, the optimal secrecy throughput can be obtained by jointly designing the spectrum sensing blocklength and transmission blocklength.
• Numerical and simulation results verify the correctness of the derivation.Comparing with other benchmark schemes,it can be found that the proposed secure transmission scheme can achieve better secrecy performance.
The remaining parts of this paper is organized as follows.In Section II,the system model is proposed.In Section III,the secrecy performance and optimization scheme of the system are studied.In Section IV, the numerical results and discussions.Finally, a conclusion is made in Section V.
II.SYSTEM MODEL
Figure 1 shows a dual-hop wiretap network in cognitive IoT, which consists of a secondary transmitter(Alice), a relay (Relay), a secondary receiver (Bob)and a primary user(PU).There is a passive eavesdropper (Eve) overhearing to the information in this network.Assuming there is no direct link between Alice and Bob due to shadow fading.Specifically, secondary transmitters (Alice and Relay) need to sense the idle spectrum of PU to access.In the first transmission slot, Alice sends the signal to Relay.In the second transmission slot,Relay uses decode-and-forward(DF)method to forward the signal to Bob.In this process, Eve eavesdrops on the information in the two transmission slots.We consider the scenario where IoT devices(Alice,Bob and PU)with a single antenna are limited by energy and computing power.Due to the strong energy and computing power, the Relay is equipped withKRantennas.Considering the worst case,Eve withKEantennas has strong eavesdropping ability.For many cognitive IoT applications,e.g.data gathering, inference and control, the typical form of data is short packets.Secondary transmitters sendTbbits in each short-packet transmission slot.
In the system, we define all channel coefficient of links follow independent identically distributed(i.i.d.)Rayleigh fading.hAR, hRB, hAE, hREdenote the channel matrix between Alie and Rlay,Relay and Bob,Alice and Eve, Relay and Eve, respectively.Specifically, the channel gainsE=λX,X ∈{AR,RB,AE,RE}, whereE[·] denotes the expectation operation.The channel is a flat fading channel in each transmission slot and the additive white Gaussian noises(AWGN)at receivers(Relay,Bob and Eve) all obey distributionCN(0,σ2).The interference caused by PU follows a Gaussian distribution obeyingCN(0,γPσ2)[21], whereγPis the signalto-noise ratio (SNR) of primary signals at secondary receivers.
2.1 Frame Structures
Figure 1 shows the frame structures of both primary and secondary users.Due to the use of short packets,we assume that only one frame is transmitted in each transmission slot.The blocklength of each frame is denoted asNchannel uses, which can be characterized as time and spectrum used to transmit information.In each frame,the licensed spectrum has two states: idle or busy.In addition, we assume that the secondary transmitters must perform sensing and data transmission in each transmission slot.Furthermore, the secondary user send signals only when the spectrum is idle.Each fame of secondary users is assumed to be synchronized with PU and consists of two successive phases,i.e.,spectrum sensing phase with the duration of blocklengthNsand data transmission phase with the blocklengthN −Ns.
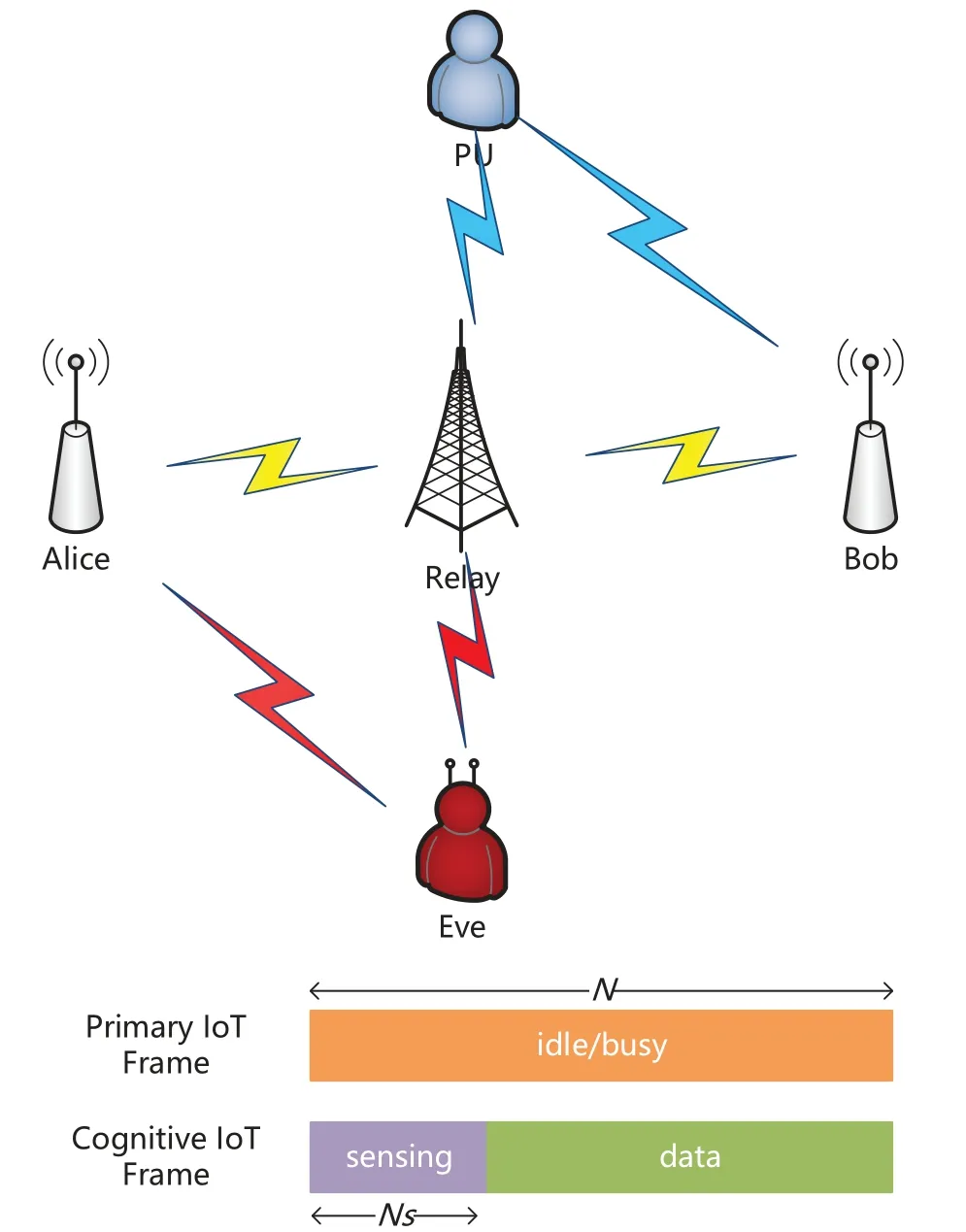
Figure 1. System model.
2.2 Spectrum Sensing Model
In each spectrum sensing phase,secondary transmitter needs to determine whether the spectrum of PU is idle or busy.Here, we denoteH0andH1as the idle and busy states of the target licensed spectrum,and denoteθH0andθH1as the prior probabilities ofH0andH1,respectively.Due to imperfect sensing,the sensing result may be incorrect.Then,the relationship between the detection probabilityθdand the false alarm probabilityθfby energy detector is[21]
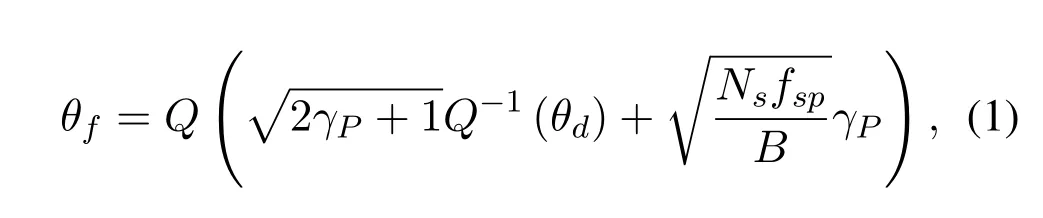
wherefspis the sampling frequency at secondary receivers,and is the tail distribution function of the standard normal distribution.θdandθfare determined byNs.In the rest of this paper, we will useθd(Ns)andθf(Ns)instead ofθdandθf,respectively.
2.3 Physical Layer Security Scheme
In order to protect private information in the cognitive IoT, we design a secure transmission scheme.In this system, DF mode is used to transmit information in the second transmission slot.In the first slot, Relay and Eve receive the signal from Alice.Due to Relay equipped with multiple antennas,the MRC scheme is adopted to strengthen the signal detection.
In the second transmission slot, Relay encodes the signal using the linear processing scheme, namely ZFB.The ZFB scheme means that the Relay sends decoded signals through zero-forcing Eve.According to the ZFB strategy, the optimal wZFis the solution of the following optimization problem:
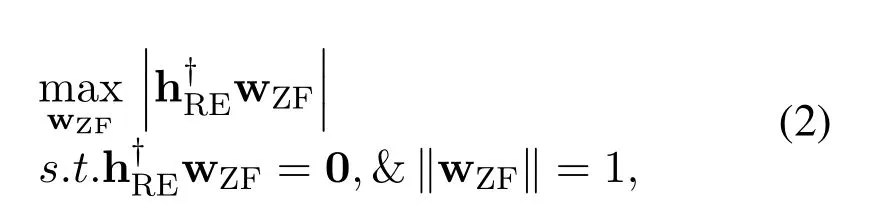
where†is the conjugate transpose operator.
With the help of the projection matrix theory,we can get the weight vector wZFas
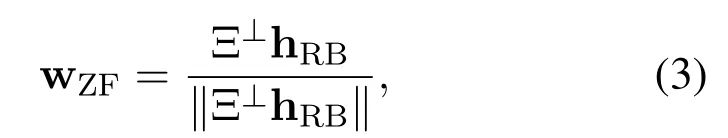
where Ξ⊥=is the projection idempotent matrix with rankKR −KE −1.To satisfy the ZFB strategy, it should satisfyKR >KE.
2.4 Achievable Transmission Rate With Finite Blocklength
According to the classic Shannon information theory,the information communication rate can reach the Shannon upper bound.However, the decoding errors will inevitably occur at the receiver in actual shortpacket communications when the blocklength is finite.According to [15], the achievable secrecy rate in short-packet communications is different from traditional physical layer security system.For a given blocklengthNof each frame and the blocklengthNsof the spectrum sensing phase,under the decoding error probabilityεand the information leakageδconstraints,the secrecy rateRsis given by
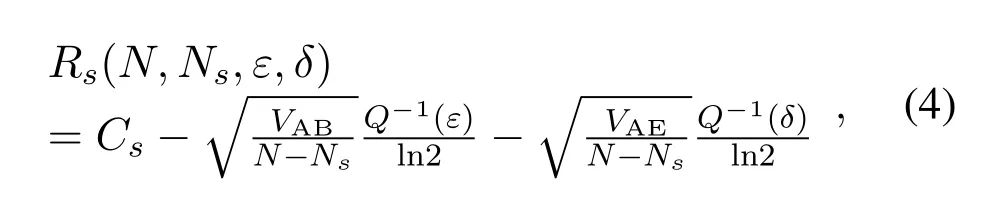
whereCs=log(1+γAB)−log(1+γAE)is the secrecy capacity, which denotes the traditional secrecy capacity,andVX=1−(1+γX)−2,X ∈(AB,AE)is the channel dispersion,whereγXis the SNR in linkXat the reciever.In(4),by the definition ofCs,Cs ≥0,i.e., it has to satisfy conditionγAB > γAE.Assuming that the amount of informationTbtransmitted is fixed, the transmission time increases with the blocklength.In cognitive IoT, lower delay can be guaranteed by shorter blocklengthN[22].
III.SECRECY PERFORMANCE ANALYSIS
In this section, we investigate the average secrecy throughput in cognitive IoT.First, we find a closedform approximate expression of the average secrecy throughput.Then, the average secrecy throughput is studied in the high-SNR regime and infinite blocklength, respectively.Finally, a Fibonacci-based alternating optimization method is proposed to design optimal blocklengthNand spectrum sensing blocklengthNsto maximize the average secrecy throughput.
3.1 Secrecy Throughput Approximation
The average secrecy throughput is defined as the average secrecy rate at which data packets can be reliably transmitted under certain secrecy constraints.Specifically,it means that Alice transmitsTbinformation bits for each short-packet transmission, and the blocklength actually can be used to measure the transmission latency [23], which is equivalent to a given transmission rateWhenγAB > γAE, and the limitation with the information leakage probability constraintδ, the decoding error probabilityεis given by
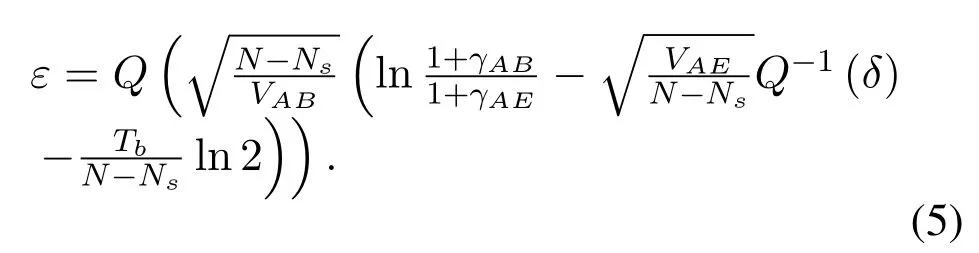
WhenγAB < γAE,Cs= 0.Therefore,we setε=1.
For a fixed transmission informationTbbits with blocklengthNand spectrum sensing blocklengthNs,the average achievable secrecy throughput measured in bits per channel use (BPCU) is formulated in [15]as
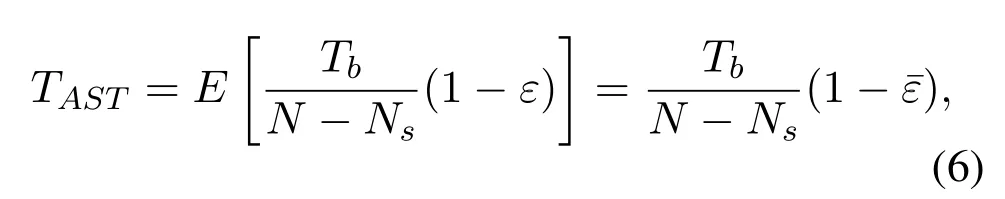
Furthermore,due to the imperfect spectrum sensing,there are two cases that secondary transmitters may transmit cognitive data in each transmission slot.In the first case, the idle licensed spectrumH0is correctly detected.In the second case, the busy licensed spectrumH1is considered to be idle.In particular,we assume that the two transmission slots are detected independently, and there will be four cases, which are(1−θf(Ns))2,θH0θH1(1−θf(Ns))(1−θd(Ns)),θH1θH0(1−θf(Ns))(1−θd(Ns)),θH1θH1(1−θd(Ns))2,respectively.Thus,the average decoding error probability can be derived as

where1,2,3,4}means the four cases.Besides, the received SINR at receivers underHj(j ∈{0,1}) iswhereX ∈{AR,RB,AE}.Thus, the instantaneous signal to interference plus noise ratio(SINR)at Relay,Bob and Eve can be given by

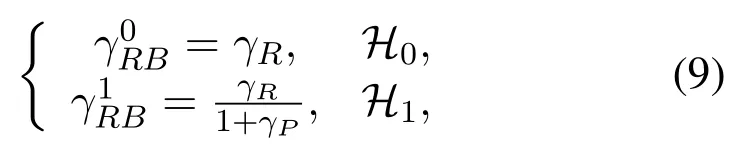
and

The steps of the proposed analytical framework for the secrecy throughput are given as follows:
Step 1:In order to solve(6), we can first solve for the average decoding error probability in(7).Considering the imperfect spectrum sensing,secondary transmitters may transmit cognitive data when the idle licensed spectrum is correctly detected or the busy licensed spectrum is considered to be idle in two transmission slots, respectively.Therefore, we can divide the average decoding error probabilityin (6) into four cases to obtainandin (7), respectively.
Step 2:In the first case, Alice and Relay transmit data when the idle licensed spectrum is correctly detected.Thus,γAR=,γRB=andγAE=Due to the DF forwarding scheme,the instantaneous SINR from Alice to Bob is

The average decoding error probability of the first case in(7)can be derived as
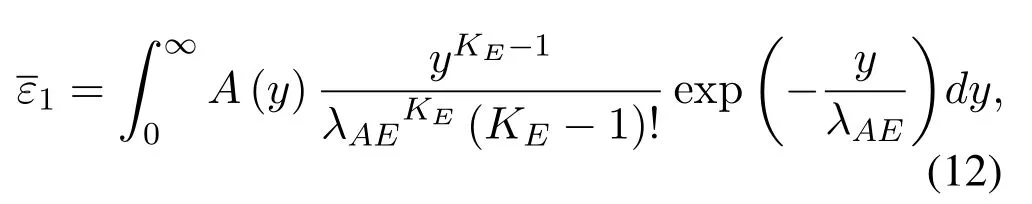
where
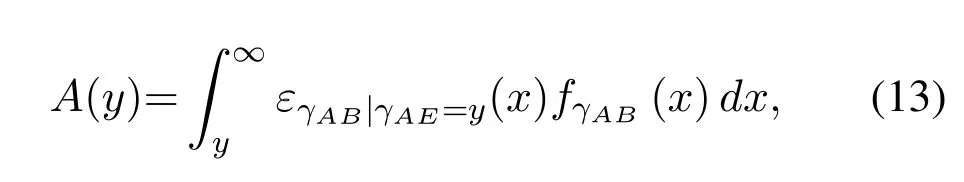
whereεγAB|γAE=y(·) defines the conditional decoding error probability whenγAE=yandγAB=x.The main difficulty of solving the average decoding error probability in (12) is the solution ofA(y) in(13), where the functionεγAB|γAE=y(·) has the form ofQfunction.To solve this problem,we approximateεγAB|γAE=y(·).
With the help of [16] and [24], the first-order approximation ofεγAB|γAE=y(x)can be expressed as
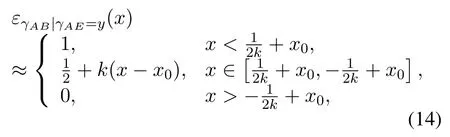
where
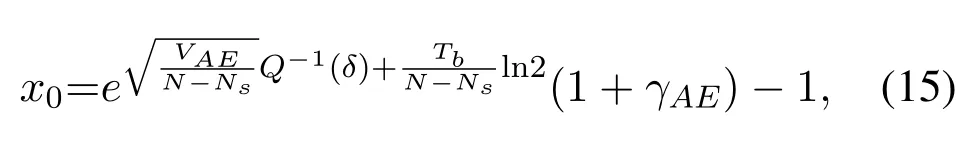
and
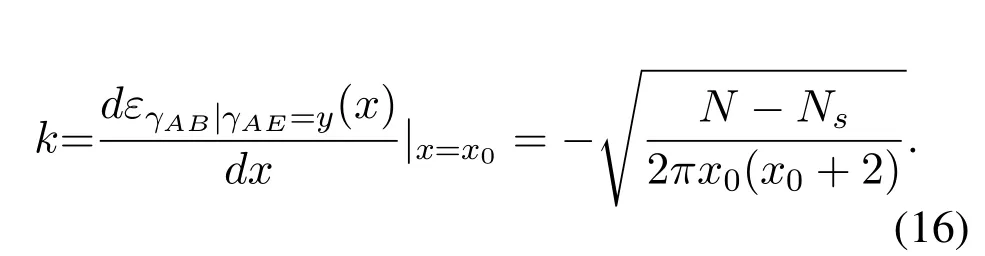
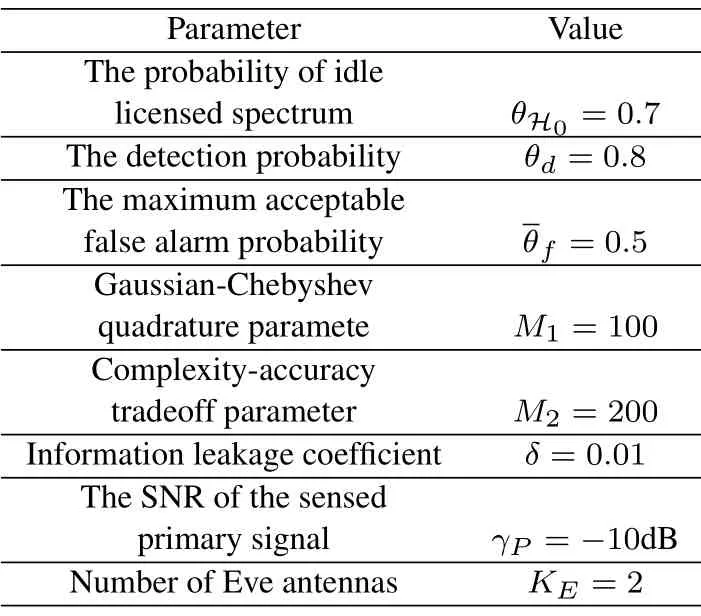
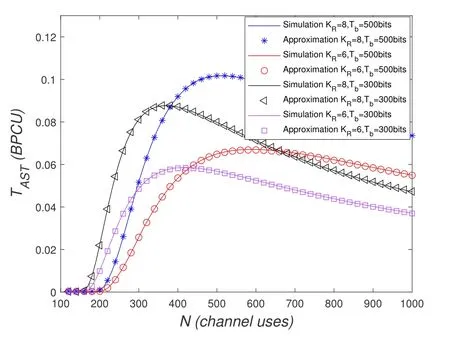
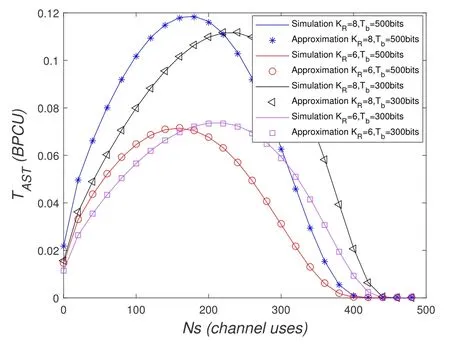
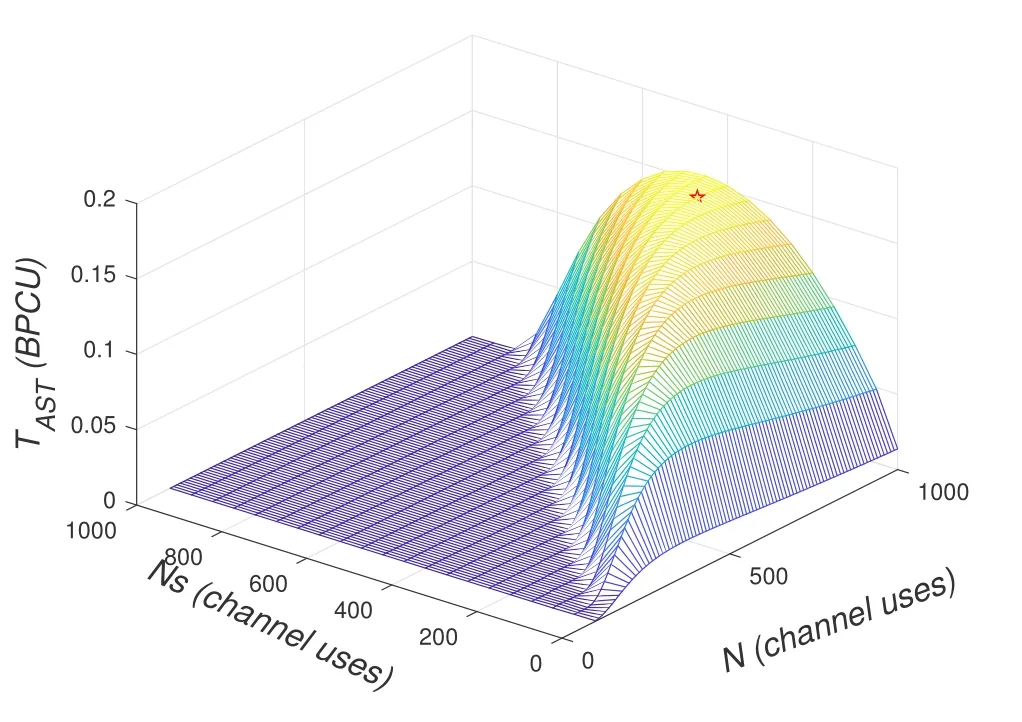
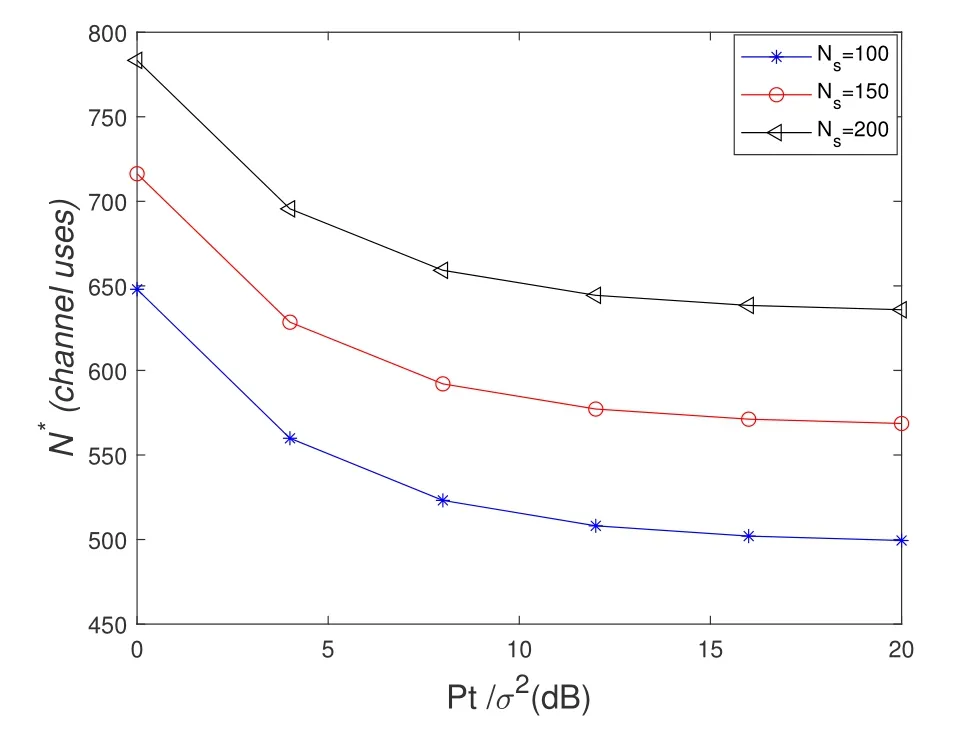
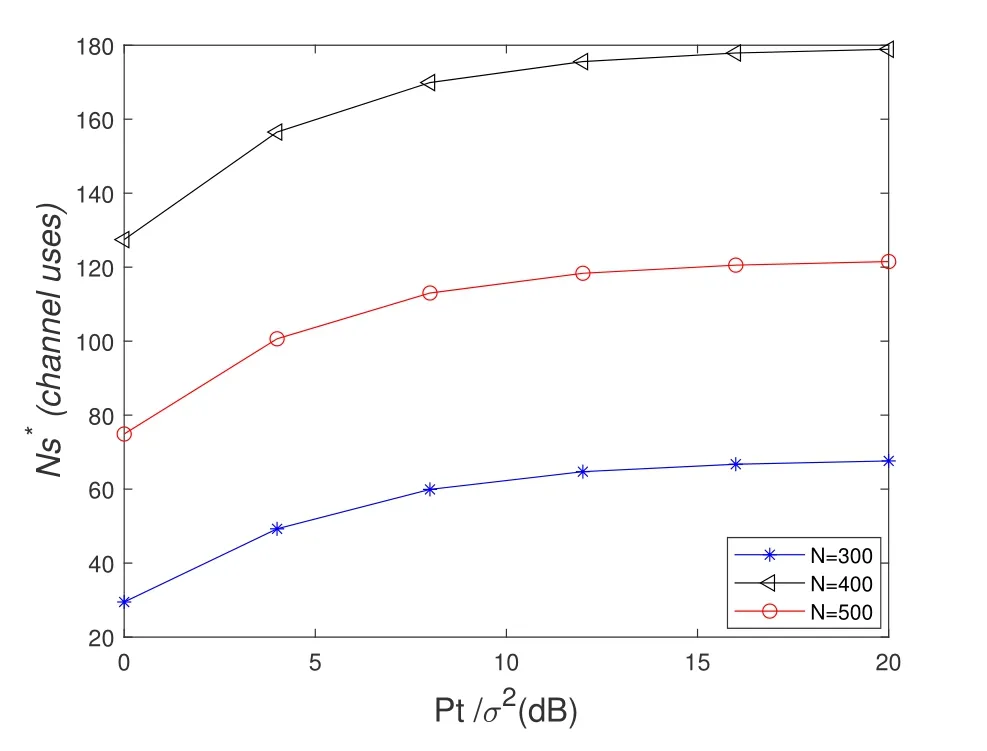
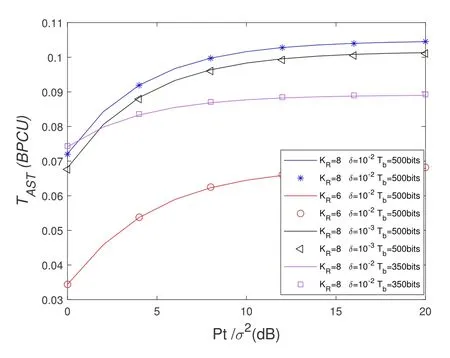
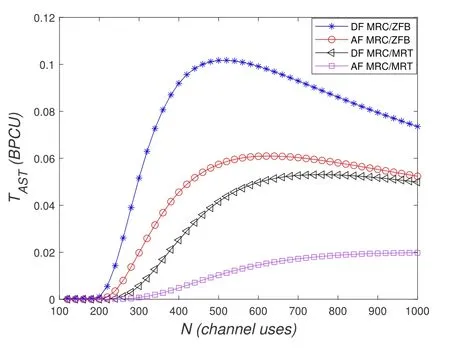
To solveA(y)in(12),the lower limit of the integral in (13) can be changed fromyto 0 based on the fact thatεγAB|γAE=y(x)>1/2 whenx The integralA(y) is approximated as (17) by the above approximate transformation. To investigate more insights about the secrecy throughput, some approximations in the moderateblocklength regime, i.e., 102< N <103, will be carried out.It is worth noting that the case of 102 Step 3:Next, the cumulative distribution function(CDF)of Bob’s SNR and the probability density function(PDF)of Eve’s SNR can be given by,respectively and Then, substituting (19) and (20) into (12), the secrecy throughput under finite blocklength is approximated as where where Φ2is shown as(23) andM1is a sufficiently large parameter to ensureVAE ≈1 whenγAE > M1,M2is a parameter for the complexity-accuracy tradeoff,withx0(z) =x0|γAE=z,fϕ1(z) =A(x0(z))fγAE(z),tn= cosandϖ1=The detailed derivation of(21)is shown in Appendix A. Step 4:In the same way,the values ofandcan be obtained in Appendix A.Then,we can substitute,andinto(7)to get the result. The analytical framework for the average secrecy throughput and obtaining a closed-form expression for short-packet communications in cognitive IoT is summarized in Table 1. Table 1. The analytical framework for the average secrecy throughput. We analyze the approximative secrecy throughput of cognitive wiretap channels under∞.In this case,the interference caused by PU can be ignored.Thus,TASTin the high-SNR regime is given by the average decoding error probability cannot decrease to zero as the transmit power approaches infinity,since both the SNRs at Bob and the Eve increase at the same time. For the classical case with infinite blocklength, whenN →∞, the decoding error probabilityε →0 as long asγAB > γAE.Thus, with infinite blocklength,the secrecy throughput defined in(6)can be expressed as Moreover, whenN →∞and→0, we can degenerate it into a model that generally does not consider the blocklength.At this point, we can analyze the secrecy performance of the system by solving Pr(γAB >γAE), which represents non-zero secrecy capacity [25].By solving Pr(γAB >γAE), we can get the expression for the probability of the non-zero secrecy capacity as follows. where In this subsection, we optimize the spectrum sensing blocklengthNsand the frame blocklengthNto maximize the average secrecy throughput. Considering the constraints of minimum detection probability and maximum false alarm probability, the optimization problem is given by Before solving (P1), we have the following Lemma 1. Lemma 1.The objective function TAST decreases with θd. Proof.See Appendix B. Then, the optimization problemP1can be transformed into ConsideringNandNsare coupled with each other,the optimization problem is difficult to solve directly.In this regard, we apply the primal decomposition method to optimize the spectrum sensing blocklength and packet blocklength,respectively. whereN(τ)andare the optimal packet blocklength and sensing blocklength at theτ-th iteration,respectively. Due to the complexity form ofTAST,it is not easy to verify the convexity of(P2).In this case,for each optimization parameter,we resort to the Fibonacci-Search Method to find a suboptimal solution.The detailed procedure is given by Algorithm 1. Algorithm 1. The secrecy throughput maximum algorithm.1: Initialize τ =1,τmax =20;2: while τ ≤τmax do 3: Let Na =0 and Nb =Nmax,4: Find the minimum ς satisfying Fibo(ς)≥Nb −Na,N1 =Nb −Fibo(ς −1), N2 = Na + Fibo(ς −1).Compute ˜TAST,1 =˜TAST (N1), ˜TAST,2 = ˜TAST (N2),Repeat.5: if ˜TAST,1 > ˜TAST,2 then 6: Nb =N2,N2 =N1, ˜TAST,2 = ˜TAST,1,N1 =Nb −Fibo(ς −1),˜TAST,1 = ˜TAST (N1).7: else 8: Na =N1,N1 =N2, ˜TAST,1 = ˜TAST,2,N2 =Na −Fibo(ς −1),˜TAST,2 = ˜TAST (N2).9: end if 10: Update ς =ς −1.Until ς ≤1.11: if ˜TAST(N(τ))≥˜TAST(N(τ−1))then 12: N(τ) =N1.13: end if 14: Let Ns,a = ˜θ−1 f(¯θf),Ns,b =N(τ).15: Find the minimum ς satisfying Fibo(ς) ≥Ns,b −Ns,a,Ns,1 =Ns,b −Fibo(ς −1), Ns,2 = Ns,a + Fibo(ς −1).Compute ˜TAST,1 = ˜TAST (N1), ˜TAST,2 = ˜TAST (N2),Repeat.16: if ˜TAST,1 > ˜TAST,2 then 17: Ns,b =Ns,2,Ns,2 =Ns,1, ˜TAST,2 = ˜TAST,1,Ns,1 =Ns,b −Fibo(ς −1),˜TAST,1 = ˜TAST(Ns,1).18: else 19: Ns,a =Ns,1,Ns,1 =Ns,2, ˜TAST,1 = ˜TAST,2,Ns,2 =Ns,a −Fibo(ς −1),˜TAST,2 = ˜TAST(Ns,2).20: end if 21: Update ς =ς −1.Until ς ≤1.22: if ˜TAST(N(τ)s)≥˜TAST(N(τ−1)s)then 23: N(τ)s =Ns,1.24: end if 25: τ =τ +1.26: end while In this section, we give the numerical analysis of the above derived results.By comparing the theoretical analysis with the results of the Monte Carlo simulation, we can verify the accuracy of the derived theoretical value and get some useful insights that are put forward for the system performance.According to[21,16],unless otherwise stated,the simulation parameters are listed in Table 2.All the simulation results shown in this paper are obtained by averaging over 100,000 simulation tests. Table 2. Parameter setting in simulation. Figure 2 shows the average secrecy throughputTASTversus blocklengthNwith different system parameters whenPt/σ2= 10dB.It can be seen from the figure that the secrecy throughputTASTis a con-vex function of the blocklengthN.According to(5),theis a monotonically decreasing function of theNwhenNsis fixed.And the transmission time increases with the blocklengthNwhenTbis fixed.Therefore,there is a trade-off betweenTASTandNunder security constraints.In addition,the conclusions obtained by comparing the curves with different parameters are in line with expectations.We can demonstrate that the secrecy throughputTASTof the system can be significantly improved by increasing the number of transmission antennasKRand transmission information bitsTb. Figure 2. The average secrecy throughput TAST and its approximations versus blocklength N. Figure 3 shows the average secrecy throughputTASTversus blocklengthNswith different system parameters whenPt/σ2=10dB.Similar to the result in Figure 2,the secrecy throughput is also a convex function of the spectrum sensing blocklengthNs.There is a trade-off betweenTASTandNs.It can be observed from (1) that the false alarm probabilityθfdecreases asNsincreases, since largerNsmakes sensing more accurate.However,the larger sensing blocklengthNs,the smaller transmission blocklengthN −Ns, resulting in a large decoding error probability.Therefore,the system needs to design an optimalNsto maximizeTAST.In addition,the secrecy throughputTASTof the system can be improved by increasing the number of transmission antennasKRand transmission information bitsTb. Figure 3. The average secrecy throughput TAST and its approximations versus spectrum sensing blocklength Ns. Figure 4 shows the average secrecy throughputTASTversus blocklengthNand spectrum sensing blocklengthNswhenPt/σ2= 10dB.According to the conclusion of Figure 2 and 3,there are optimalNand optimalNsto maximizeTASTwhen the information bitsTbis fixed.We can jointly design the optimal (N∗,) according to the proposed Fibonaccibased alternating optimization method.According to the simulation results, the optimal value obtained by the proposed algorithm is almost the same as that by the two-dimensional exhaustive search, and the complexity of the proposed algorithm is greatly reduced. Figure 4. The average secrecy throughput TAST versus blocklength N and spectrum sensing blocklength Ns. Figure 5 shows the optimalN, i.e.,N∗, maximizing the average secrecy throughputTASTobtained from the Fibonacci-based optimization method whenKR= 8 andTb= 500bits.As the figure shown, the optimalN∗slightly declines asPt/σ2increases from 0dB to 20dB.This verifies the explanation of Figure 2 that there is a trade-off betweenTASTandN.In addition, it illustrates that with the increase ofPt/σ2, the optimal blocklengthN∗decreases when the sensing blocklengthNsandTbare fixed.That is to say, we can reduce the blocklengthN(transmission time) by increasingPt/σ2. Figure 5. Optimal blocklength N,i.e.,N∗versus Pt/σ2. Figure 6 shows the optimalNs, i.e.,versusPt/σ2whenKR= 8 andTb= 500bits.WhenNis a fixed value,sinceTbdoes not change,the optimal sensing blocklengthNsincreases asPt/σ2increases.This shows thatTASTcan be maximized by choosing an optimal sensing blocklength whenNis fixed.This can provide guidance for designing the sensing blocklengthNsaccording toNin cognitive IoT. Figure 6. Optimal blocklength Ns,i.e.,versus Pt/σ2. Figure 7 shows the average secrecy throughputTASTversusPt/σ2with different system parameters.It is shown in figure that the secrecy throughputTASTincreases as the transmit power increases at low SNR.However, the security throughputTASTreaches the performance bound due to the limit of the transmit informationTbwhen the transmission power reaches a certain bound.This guides us to reduce the transmission power and energy consumption as much as possible while meeting the requirements ofTASTin practice.In this case,the secrecy throughputTASTcan be further improved by increasing theTb.Furthermore,we can increase the number of Relay’s antennasKRto improve the secrecy throughputTASTby using space diversity. Figure 7. The average secrecy throughput TAST and its approximations versus Pt/σ2. Figure 8 shows the average secrecy throughputTASTversus blocklengthNunder different transmission schemes.We have compared the secrecy performance of MRC/MRT and MRC/ZFB transmission schemes,both of which can effectively improveTAST.However, MRC/ZFB can obtain a largerTASTdue to the zero-forcing of Eve.In addition,the DF forwarding scheme is used to decode information at Relay,which can reduce packet error probability and further improve the secrecy performance of the system.Comparing these schemes, the MRC/ZFB scheme in DF mode has better secrecy performance, which shows the effectiveness of the proposed scheme. Figure 8. The average secrecy throughput TAST versus blocklength N under different transmission schemes. This paper investigates the secrecy performance of relay-assisted short-packet communications in cognitive IoT with spectrum sensing.Specifically, we use MRC/ZFB scheme to restrict the eavesdropping.Then,we derive the approximate expression of the average secrecy throughput of the short-packet communications for cognitive IoT.In addition,the expression with high-SNR regime and blocklengthN →∞are derived to analyze the impact of system parameters on secrecy performance.Furthermore, we can jointly optimize spectrum sensing blocklength and transmission blocklength to maximize the security throughput.Moreover, it can be clearly found that the proposed scheme achieves better secrecy performance than benchmark schemes.In the future, a promising direction is to study the secrecy performance of massive IoT devices with random deployed and low power,which is more realistic. ACKNOWLEDGEMENT This work was supported by Natural Science Foundation of China (No.62171464, 61801496 and 61771487).This paper was presented in part at the 2021 IEEE International Conference on Communications Workshops(ICC Workshops),2021. APPENDIX A Substituting(19)into(18), we take the results as follows. Next, substituting (39) into (12) and after some mathematical integral operation,can be derived as With the help of Gaussian-Chebyshev quadrature,the integral Φ1Gis approximated as Through the integral operation, Φ2Gcan be expressed as(23). In the same way,the values ofandcan be obtained as follows. APPENDIX B Sinceθfis a function ofθd,we first solve for the first derivative ofθfwith respect toθd,which is given by Hence,the false alarm probabilityθfincreases with the detection probabilityθd.Next, the first derivative ofTASTwith respect toθdis According to (46), we can obtain thatTASTdecreases withθd.
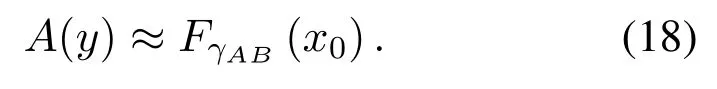
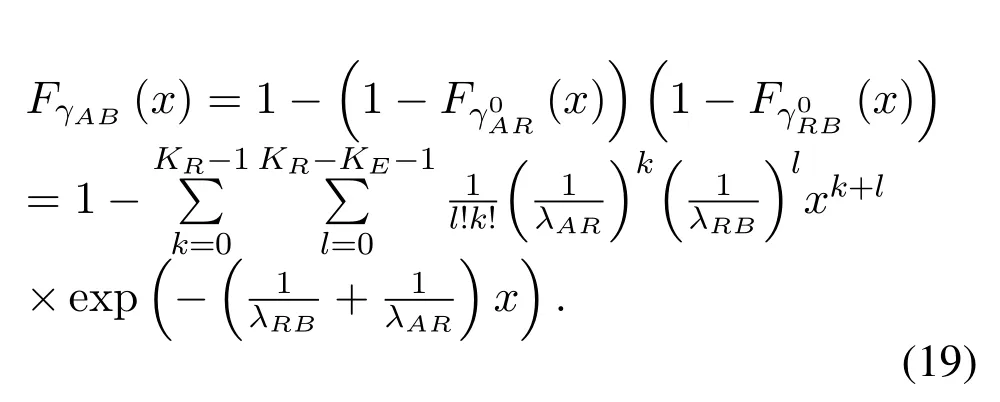
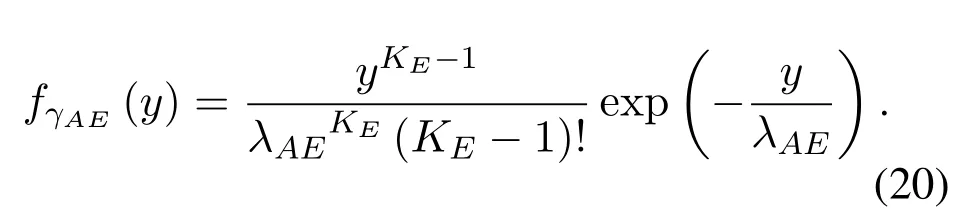
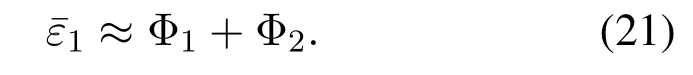
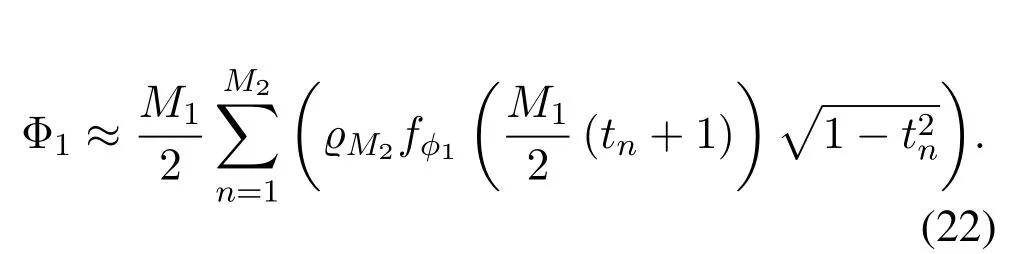
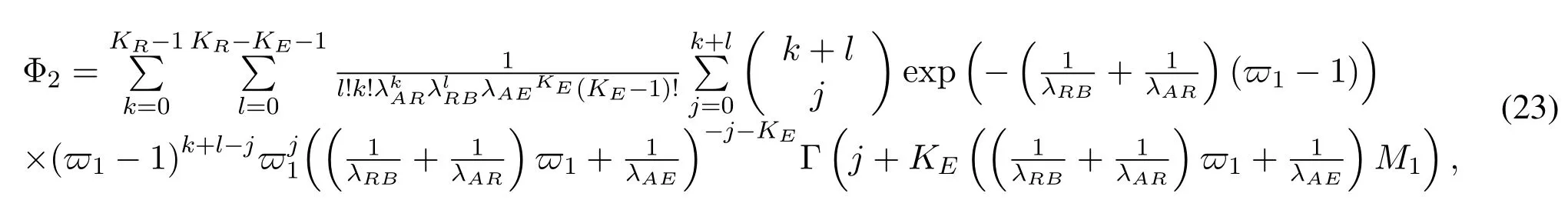

3.2 High-SNR Regime
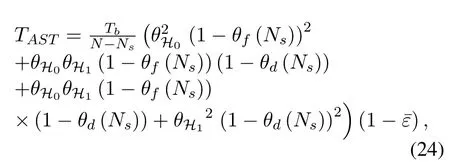
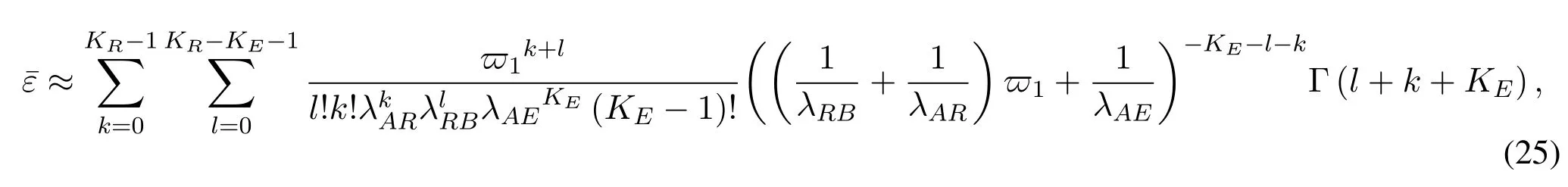
3.3 The Classical Case with Infinite Blocklength
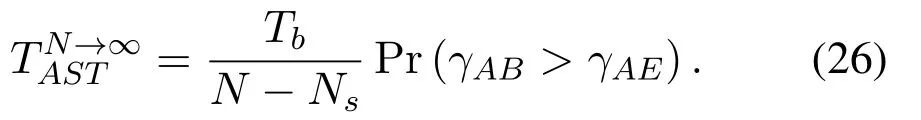
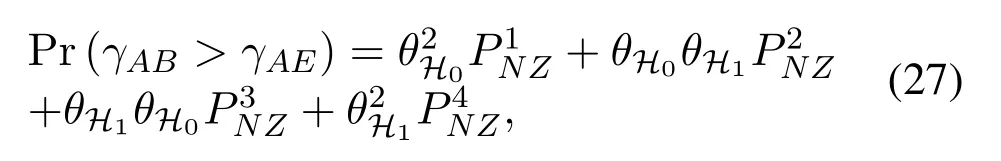
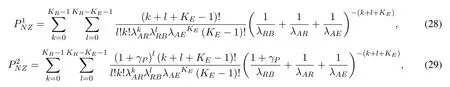
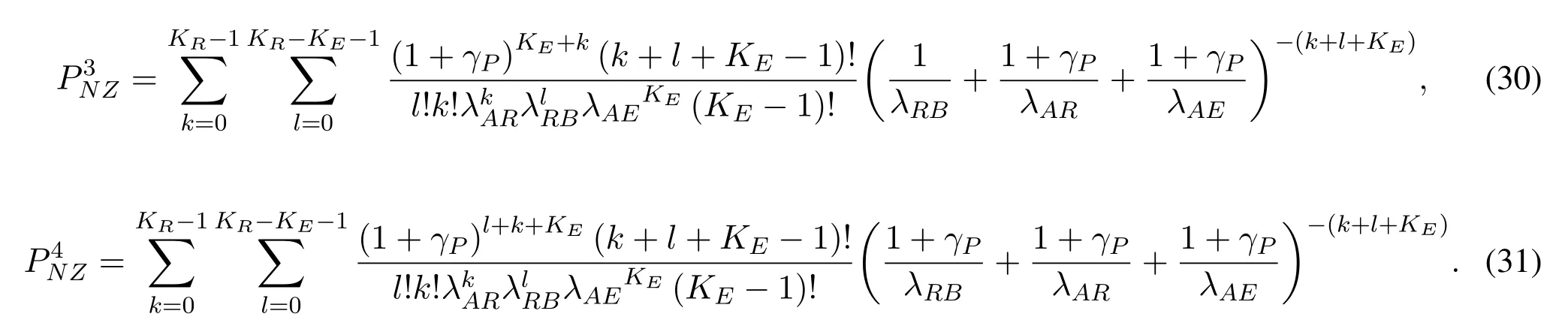
3.4 Optimize Transmission Blocklength And Spectrum Sensing Blocklength
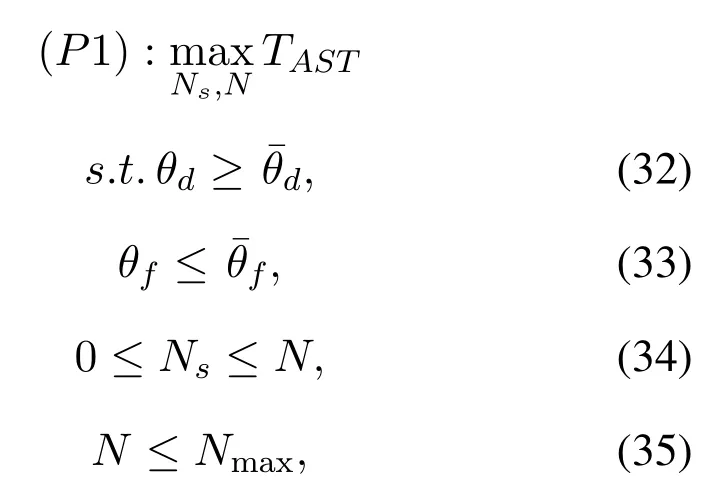

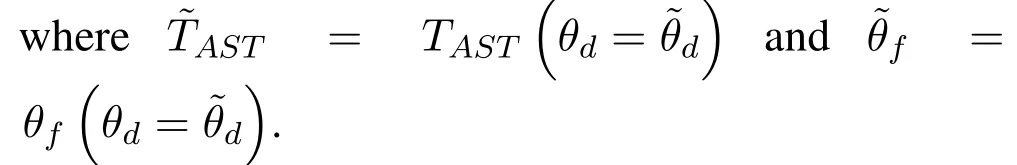



IV.SIMULATION RESULTS
V.CONCLUSION