Relay Beamforming Design for Physical Layer Secure Communication via Line Search Algorithm

Siqi Chen,Cong Sun

School of Scince,Beijing University of Posts and Telecommunications,Beijing 100876,China

Abstract: This paper considers a physical layer security model in wireless communications.Two legitimate users communicate through several relays with the presence of an eavesdropper.We jointly design the relay beamforming weights and minimize the total relay transmit power, while ensuring users’ Quality of Services and preventing the information being eavesdropped at the same time.The problem is a robust optimization problem, because of the imperfect channel state information from users and relays to the eavesdropper.First the original problem is simplified, where the high order robust terms are omitted.Then we design an iterative algorithm based on line search, by solving two Quadratically Constrained Quadratic Programming subproblems and a one-dimensional subproblem.Simulation results indicate that the proposed algorithm outperforms the state of the arts.

Keywords: wireless communication; physical layer security;line search;robust optimization

I.INTRODUCTION

Security is an important issue in wireless communications.Compared to the wired communication process, the broadcast property of wireless communication leads to poor security performances.Different technologies are applied for the transmit information protection.At the same time, energy efficiency and resource allocation are important.

Based on physical layer, the communication security technologies mainly include beamforming, artificial noise and other schemes [1–7], which improve security performances.For beamforming designing schemes, different kinds of problems as well as algorithms are proposed for different channel state information (CSI) scenarios.Perfect CSI is considered in [8–13].A relay aided wiretap network with single-antenna is studied in[8].It designs beamforming vectors to maximize the system total energy efficiency under the requirements of limiting node power and ensure a certain secrecy rate.Optimization techniques like fractional programming,exact penalty and alternative search method are used, and the nonconvex optimization model is transformed into a series of quadratic programming subproblems.Reference[13]considers cognitive two-way relay network.By designing beamforming matrices for the signal of cognitive receiver (CR), the primary transmitters (PTs)and artificial noise, the article maximizes the secrecy sum rate for PTs, guarantees the QoS for the CR and limits the transmit power of the cognitive transmitter.However, in reality, it is difficult to obtain the perfect CSI.Communication models with no CSI[14,15]and imperfect CSI[16–20]are more popular in physical layer security.For case with no CSI, the cooperative beamforming and artificial noise techniques are adopted in [14].Two different relay modes are considered, where all the relays transmit signals or only the best relay is selected to transmit information.Different optimization models are established for the two relay modes.The idea of transmitting artificial noise in the nullspace of the channel is also considered,and the achievable secrecy rate is optimized.For the network with imperfect CSI, it transmits the secure communication of a single antenna user via relays with the presence of one multi-antenna eavesdropper in [16].By optimizing the transmit covariance matrix of the beamforming vector and noise,it maximizes the worst-case secrecy rate,and uses the block coordinate descent method to transform the nonconvex problem into a series of convex subproblems.Both perfect and imperfect CSI have been considered in [17],which discusses a model with multiple users aided by a multi-antenna relay, and an eavesdropper exists.In order to maximize the worst-case secrecy rate,the article designs the beamforming vector,obtains the lower bound of the achievable rate of legitimate users by introducing auxiliary variables, and solves the corresponding optimization problem iteratively.In [18], a single-antenna relay network is considered, in which there is an eavesdropper with imperfect CSI.It establishes a robust optimization problem to protect the user’s information from eavesdropping in the worst case.The problem is tightened and solved through the line search framework, and the optimality conditions of the simplified problem are shown.

In this paper,we consider the same communication model as[18].We jointly design the relay beamforming vector to minimize the total relay transmit power,where the legitimate users’Quality of Services(QoSs)are guaranteed and the eavesdropper cannot obtain the users’ information even in the worst case.Different from [18], we propose a new simplified robust optimization problem,where all the robust parameters are preserved rather than being relaxed.An algorithm is proposed and the optimality conditions of the simplified problem are provided.

The rest of the paper is organized as follows.The half-duplex secure communication system model is shown in Section II.The original robust optimization problem is analyzed and simplified in Section III.In Section IV,a new iterative algorithm based on the line search framework is designed.Numerical simulations are shown in Section V.Conclusion is in Section VI.

Notation: CN×1stands for n-dimensional complex vectors; (·)H, (·)Tand (·)∗denote the Hermitian,transpose and conjugate of the matrix, respectively;∥·∥is the vector Euclidean norm;|·|is the absolute value;Re(·) represents the real part of scaler;Tr(·)stands for the trace of a matrix;Diag(A) is the diagonal matrix with the same diagonal entries as matrixA;Diag(a) is the diagonal matrix whose diagonal entries is the elements of vectora;(≻0)meansAis a positive semi-definite(positive definite)matrix;CN(0,σ2)denotes the Gaussian distribution,with mean as 0 and variance asσ2.

II.SYSTEM MODEL

Consider a half-duplex wiretap relay network which adopts the Amplify-and-Forward(AF)relay protocol,as in Figure 1.Two legitimate users Alice and Bob exchange messages through N relay stations.Meanwhile an eavesdropper Eve eavesdrops signals from the two users and relays.Here each user,each relay as well as the eavesdropper has single antenna.

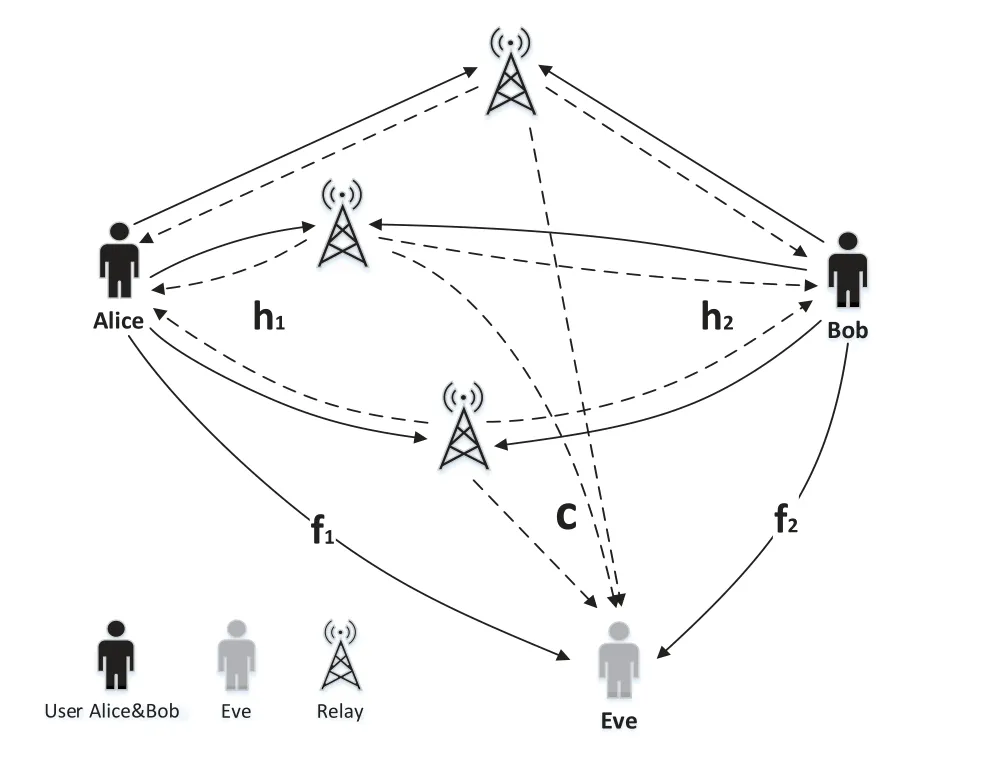
Figure 1. Wiretap relay network.

Lethj ∈CN×1,j=1,2 be the channel coefficients between two users and relays,fj ∈C,j= 1,2 andc ∈CN×1be the channel coefficients from users and relays to the eavesdropper.Since the exact location of Eve is difficult to obtain,we suppose the CSI between users and relays to the eavesdropper is imperfect:

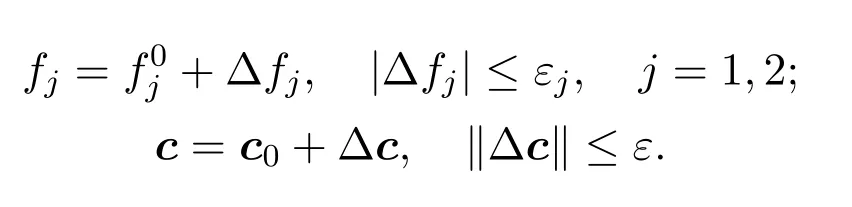
whereandc0are the estimated CSI, ∆fjand ∆care the corresponding errors.

The communication process is divided into two stages.First Alice and Bob transmit= 1,2 to all relays simultaneously, wherePjis the transmit power of thejth user;sjis the transmit signal of thejth user, which satisfies E= 1.Thus relays receive:

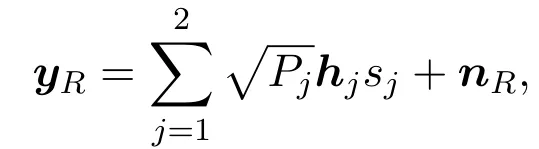
wherenR ∈CN×1is the local noise with zero mean and covariance matrix

During the second stage, each relay multiplies the received signal by the beamforming weightwi, and forwards it to the two users.Then the signals finally received by Alice and Bob are:

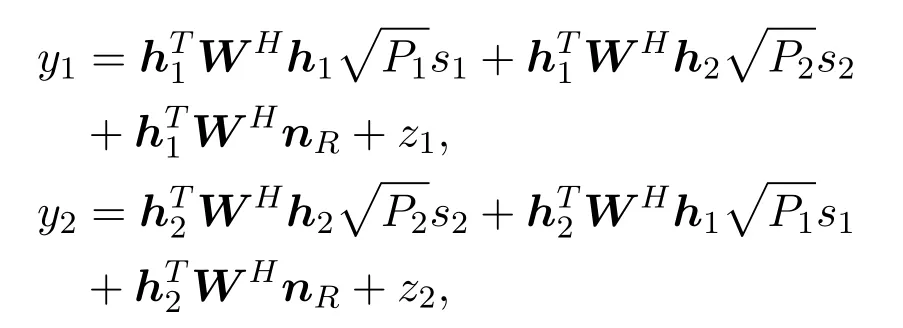
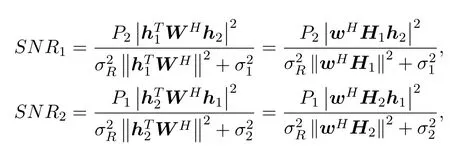
whereH1=Diag(h1) andH2=Diag(h2).In order to ensure the users’QoS,we requireSNRj(w)to be above the thresholdγj,j= 1,2.Assume that all transmit signals and noises are independent of each other.The total relay transmit power is:

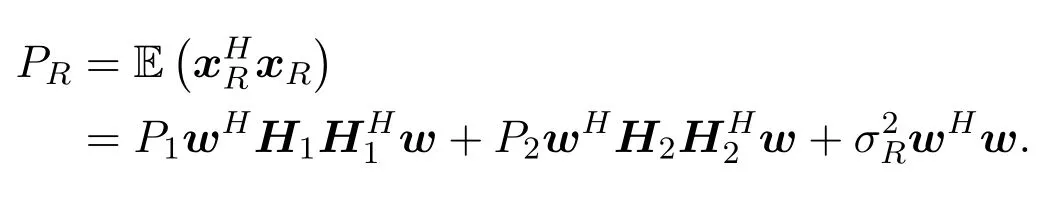
Since both users and relays broadcast signals,Eve can eavesdrop signals during both stages.The received signals of Eve in the two stages are:

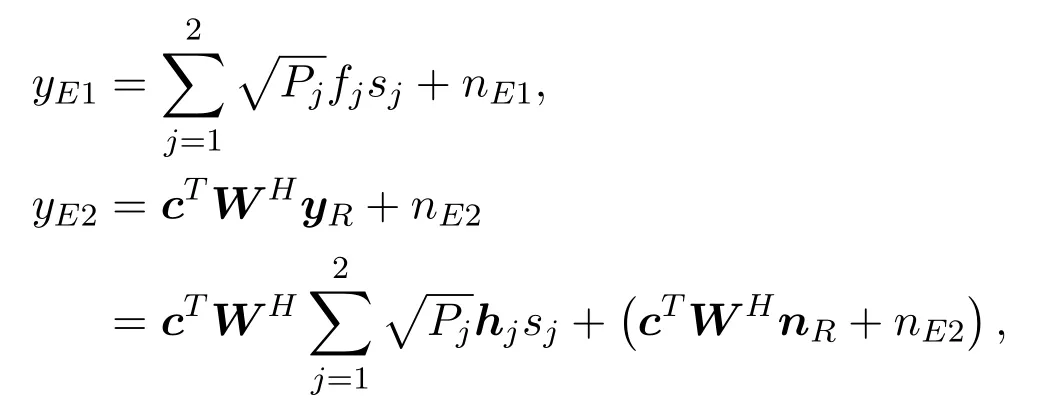
respectively.Suppose that the eavesdropper is smart enough to process the two-stage signals together.The received signals of Eve can be expressed as:yE=HEs+nE,where

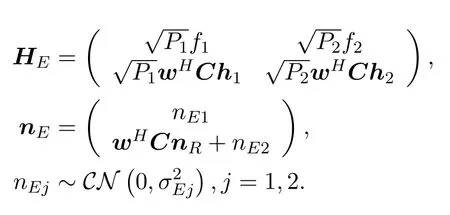
To prevent Eve from obtaining effective information,we require that its worst case achievable rateREshould be less than a thresholdrE.REis defined as

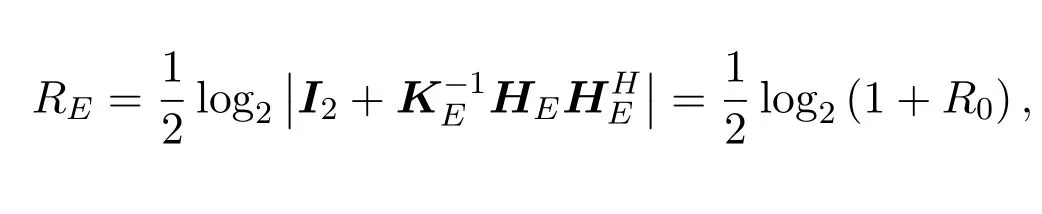
whereKE=and

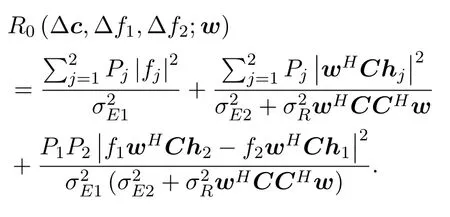
Here we design the relay beamforming vectorwto minimize the total relay transmit power,while guaranteeing the SNRs of two legitimate users above some thresholds, and at the same time requiring the worst case achievable rate of the eavesdropper to be upperbounded.The system model is summarized as follows:

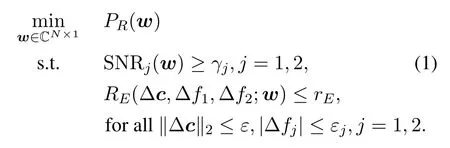
Problem (1) is a robust optimization problem.In fact, it is equivalent to a quadratic constrained quadratic programming (QCQP) problem with infinite constraints, which is difficult to deal with.The most common way to deal with robust constraints is to tighten the constraints and replace the original feasible set by its subset.This process drops all or some robust parameters and thus simplifies the problem.However,it may loss the optimality of the original problem, or even cause infeasibility.Next, we will simplify the problem while keeping all the robust parameters, and then propose an iterative algorithm to solve the simplified problem.

III.SIMPLIFIED PROBLEM

We simplify problem (1) by approximating its robust constraint.From the expression ofR0, we shall analyze the approximation step by step.

Lemma 1.Suppose x and y are two n-dimensional complex vectors.Then,Re(xHy)≤η∥y∥2holds for any ∥x∥2≤η.The equality holds if and only if x=.

From Lemma 1,we have

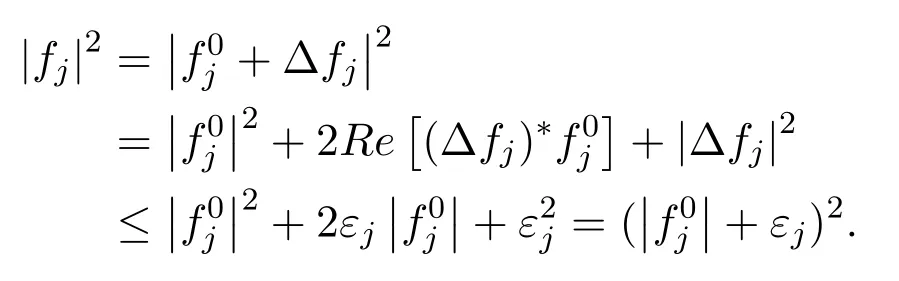
Therefore this part can be reduced to a constant

(2)Approximate the third terms:

According to(1)and(2),R0is approximated as

Now problem(1)is approximated

whereγE= 22rE −1.Next we will propose an iterative algorithm to solve the approximated problem(4a).

IV.THE ITERATIVE ALGORITHM

Problem (4a) is still a robust optimization problem.The detailed algorithm is shown in this section.

4.1 Initialization

Constraint(4c)can be equivalently transformed as

where

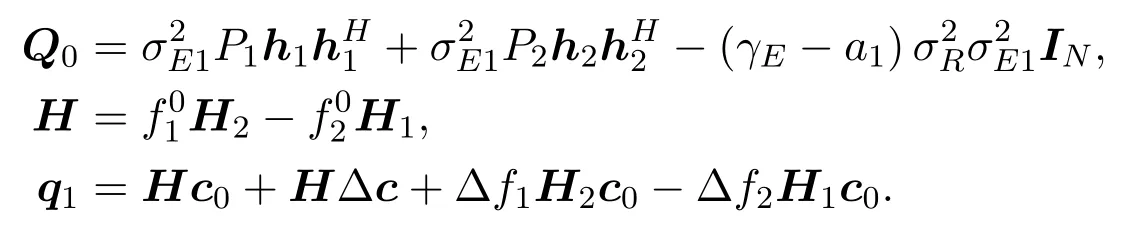
We can deduce that

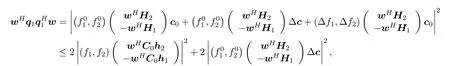
where

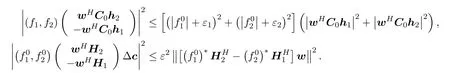
Thus we have

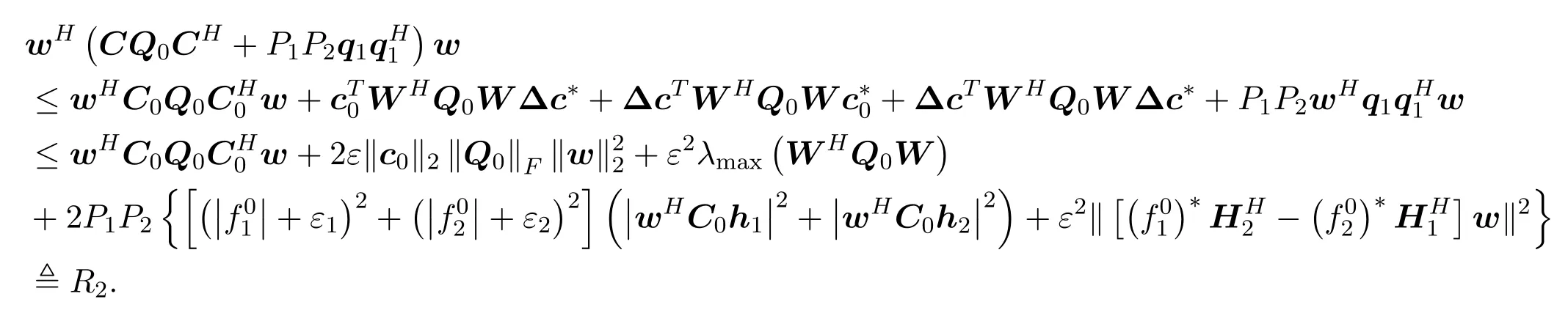
Here we tighten the robust constraint (4c) asR2(γE −a1)and solve the following problem to obtain the initial point of our algorithm:

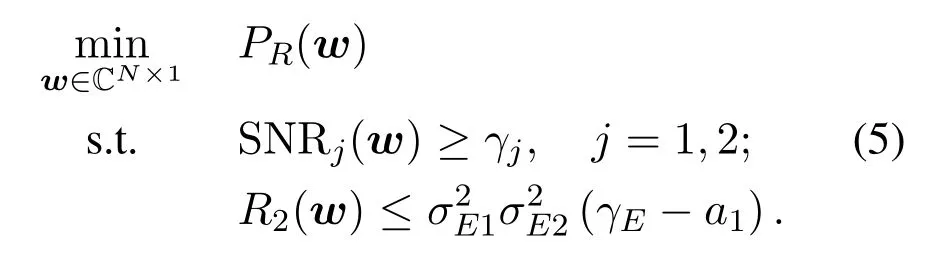
It is a typical QCQP problem with three constraints,which can be solved optimally by the semi-definite relaxation(SDR)method[21–24].It is easy to see that its feasible region is the subset of that of problem(4a).Thus the optimal solution of(5)is a feasible point of problem(4a).

4.2 The Line Search Framework

In the kth iteration,suppose we have the iteration pointwksatisfying constraints(4b)and(4c).The next feasible iteration pointwk+1is constructed by the line search framework.

First we solve the following subproblem(6)and obtain the optimal solution ∆ckand ∆=1,2:

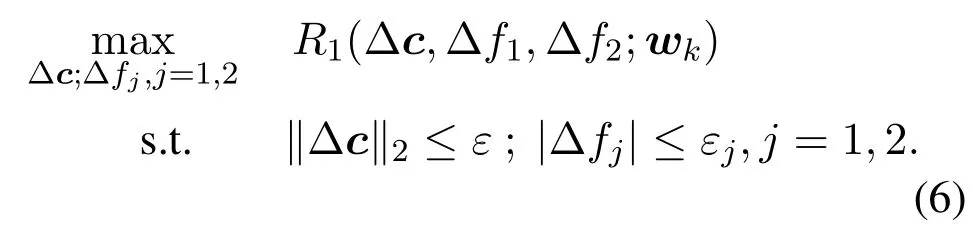
Thus problem(6)is equivalent to

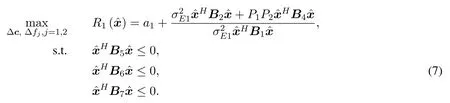
where

Letx=/r.Problem(7)is further transformed into:

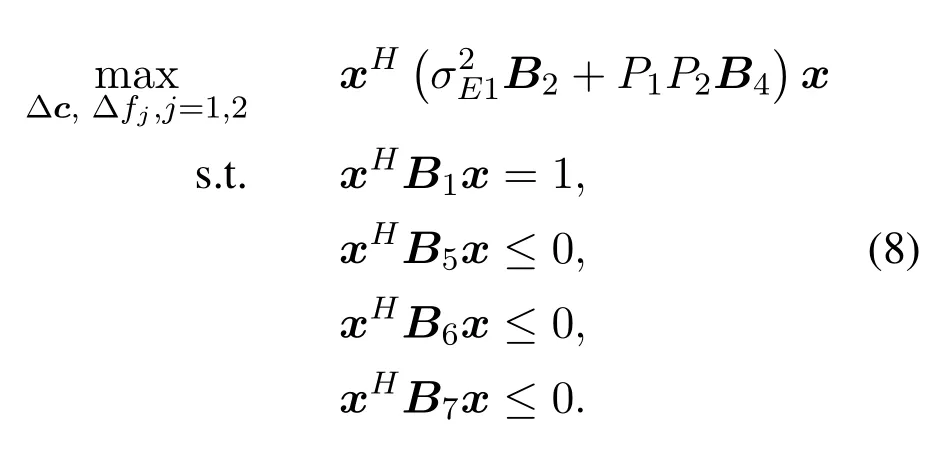
LetX=xxH.SincexHAx=Tr(xHAx) =

Tr(AxxH), problem (8) is equivalently transformed into:

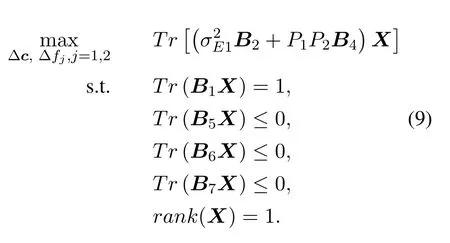
Because the rank one constraint is nonconvex, it is relaxed and the following semi-definite programming(SDP)problem is solved.

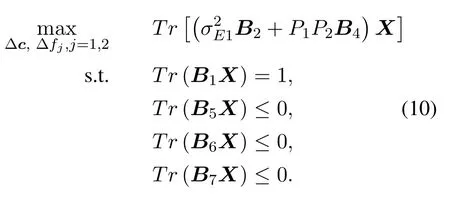
According to[23,24],there exists a rank one optimal solution of problem(10).Thus the optimal solution of problem(8)can be obtained by rank decomposition.

Next, take ∆ck,∆= 1,2 from the previous step into problem(4a)and form(11a).

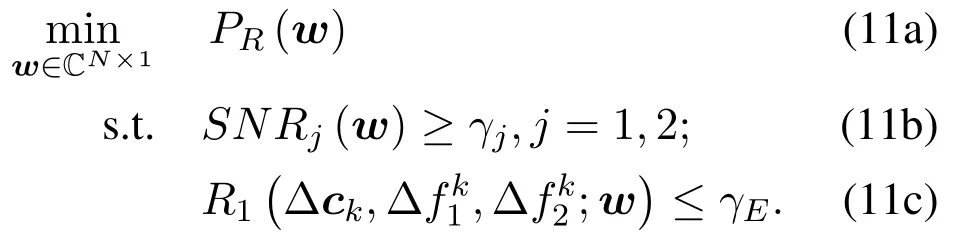
It is now a standard QCQP problem with three constraints, which can be solved by SDR method.Its optimal solutionsatisfies(11c)with parameters∆ck,∆=1,2.But it may not satisfy(4c).Next we will use−wkas the search direction to do the line search, and then find the new iteration pointwk+1,which satisfies(4b)and(4c).

We obtain the stepsizetkby solving problem(12a):

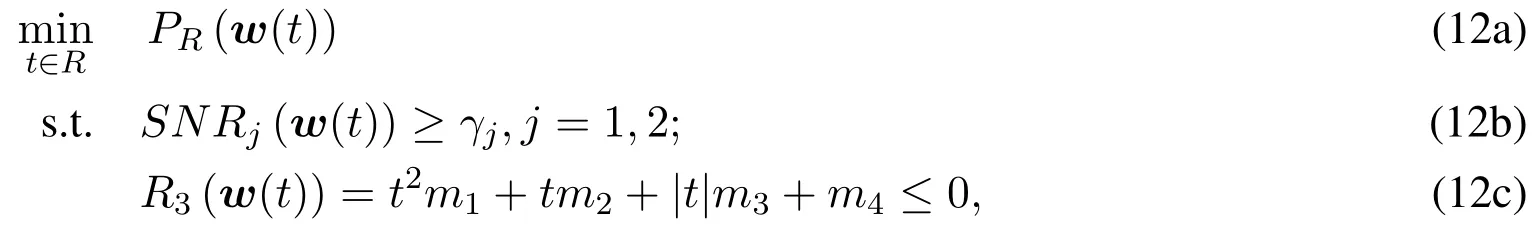
where

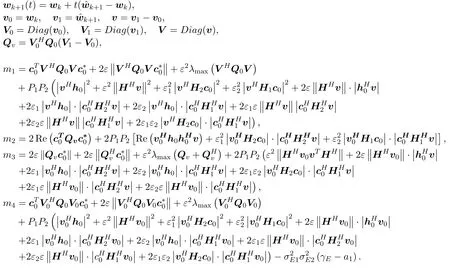
Letwk+1(tk) be the next iteration point.The following theorem guarantees that it is a feasible point of problem(4a).

Theorem 1.Suppose tk is the optimal solution of problem(12a).Then the iteration point wk+1(tk)is a feasible point of problem(4a), which is updated as wk+1(tk)=wk+tk(−wk).And the objective function of problem(4a)decreases monotonically.

The proof is given in Appendix VI.The subproblem(12a)is a one-dimensional QCQP subproblem,which is solved optimally by line segment intersections.In addition,problem(12a)always has a feasible solutiont=0,which is proved in Appendix A too.

4.3 Algorithm Framework

The complete algorithm framework is summarized as follows.

Theorem 2.If=wk, then wk is the optimal solution of problem(4a).

?

The detailed proof is provided in Appendix VI.According to Theorem 1, the obtained solution of Algorithm 1 is a feasible point of problem (4a).And the value of the objective function reduces in every iteration.As for the complexity, the main computational cost in each iteration is for the two QCQP subproblems (6), (11a)and the one-dimensional subproblem(12a).The two QCQP subproblems are both solved by the SDR method, where the complexity isO((N+3)3.5)andO((N)3.5)respectively.For the subproblem(12a), the main computational cost is the construction of the parameters,which isO((N)2).

V.SIMULATION

In this section the proposed model and algorithm are compared with the state of the arts.Here the channel coefficientshj,j= 1,2 between users and relays, are randomly generated obeying the complex Gaussian distributionCN(0,1).The estimations of the channel coefficients from users to the eavesdropper= 1,2 are randomly generated obeyingCN(0,0.01), and the upper bounds of errors are set asεj=0.015,j=1,2.The estimation of the channel coefficients from relays to the eavesdropperc0obeysCN(0,0.1),and the upper bound of error isε=0.15.σj=σEj= 1.The SNR thresholds of the two users are set asγj=γ.The achievable rate threshold of the eavesdropper isrE= 1.5.Each result is the average result of 1000 random realizations.All the tests are done by Matlab 2016b.The SDP problems are solved via CVX software.

First, we compare our proposed algorithm with the nonrobust model and [18].In the nonrobust model,all the values of ∆cand ∆fj,j= 1,2 are fixed and given.Then problem(1)is degenerated into a common QCQP problem,which can be solved optimally via the SDR method.Reference[18]considers the same system model as ours.Figure 2 shows the obtained total relay transmit power of our model, the nonrobust model and [18] under different thresholdsγand different numbers of relays.

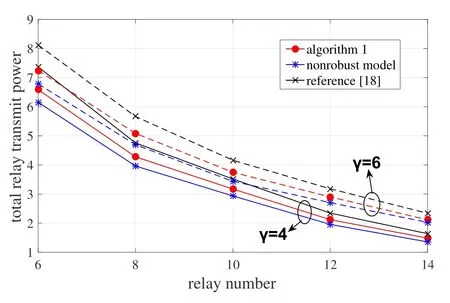
Figure 2. Comparison with the nonrobust model and[18],with respect to different thresholds γ and relay numbers.

It turns out that our model as well as algorithm outperforms [18] generally.This is reasonable, because the proposed model preserves all the robust parameters in the approximated problem while [18] only keeps ∆cin the simplified problem.Theoretically,the nonrobust model provides a lower bound for the total replay transmit power.Here the proposed model obtains higher relay power than the nonrobust model,but the gap is small.This shows the effectiveness of the proposed model and algorithm.In addition,the total relay transmit power decreases with the increment of the number of relays.It indicates the advantage of resource allocation brought by cooperation among relays.At the same time,when the SNR thresholdγincreases,the total relay transmit power increases,showing the fact that the QoSs of legitimate users are improved at the cost of the increased resource consumption.

Second, the propose algorithm is compared with[15],which considers no CSI and applies the artificial noise technique.The optimization problem considered in[15]is:

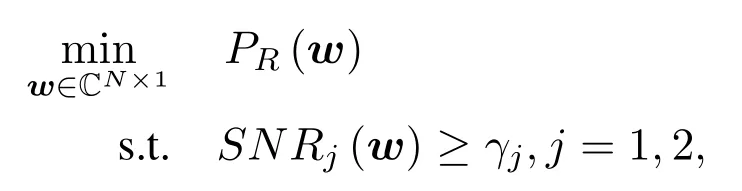
which is the same as (1) without the third constraint.The total relay transmit powerPaof [15] is divided into two parts.One part is used to transmit signalsPband the other part is used to send the artificial noisePa −Pb.The achievable rate of Eve by[15]is:

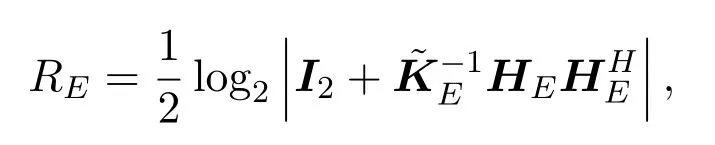
where

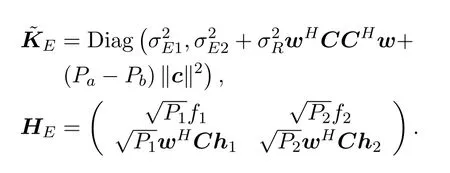
The secrecy rate is defined as:SR=(1+SNRj)−RE.

As the total relay transmit power of [15] and our algorithm are the same and fixed, the secrecy rate of the propose algorithm and [15] are compared in Figure 3 with respect to different number of relays and different signal transmit powerP=P1=P2.For a fixed relay number,the propose algorithm always outperforms [15].This indicates the importance of CSI for communication security.We can also observe that the secrecy rate increases monotonically as the relay number increases.In addition, larger transmit powerPleads to higher secrecy rate.

Third, the iteration curves of the achieved total relay transmit power with respect to different relay numbers are shown in Figure 4.Three curves have similar trends.The algorithm converges very fast in a few iterations.It also verifies the conclusion in Theorem 1 that the objective function (4a) decreases monotonically.

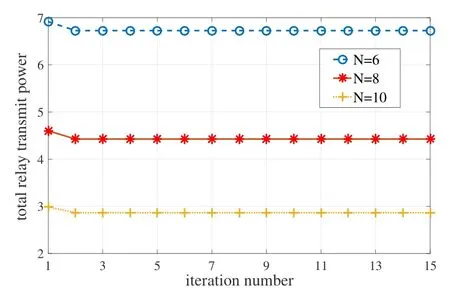
Figure 4. Convergence for N =6,8,10.

VI.CONCLUSION

In this paper,we consider a wiretap relay network consisting of a pair of users, several relays and an eavesdropper.We jointly design the beamforming weights of relays,and minimize the total relay transmit power.Meanwhile the users’ QoSs are guaranteed and the achievable rate of the eavesdropper is restrained.As the CSI related to the eavesdropper is imperfectly known, we can establish a robust optimization problem.We first approximate the problem by dropping the nonlinear terms of the robust parameters.And then an algorithm based on the line search framework is proposed.In each iteration, we solve two QCQP subproblems to find the iteration direction and a onedimensional subproblem to obtain the stepsize.In the simulation tests, the performance of the proposed algorithm is close to that of the nonrobust model; the proposed algorithm outperforms the state of the arts.The comparisons verify the effectiveness of our proposed model as well as algorithm.

ACKNOWLEDGEMENT

This work is supported by National Natural Science Foundation of China (Grant No.11771056 and 11871115), and the Young Elite Scientists Sponsorship Program by CAST(Grant No.2017QNRC001).

APPENDIX A.PROOF OF THEOREM 1

The proof consists of two parts.The first part is to prove thatwk+1(t)satisfies(4b)and(4c),for any stepsize satisfying (12b) and (12c).Thenwk+1(t) is a feasible point of problem (4a).Supposeistany stepsize satisfying constraints(12b)and(12c).Obviouslywk+1(t)satisfies(4b),because of the constraint(12b).Next we prove thatwk+1(t)satisfies(4c).

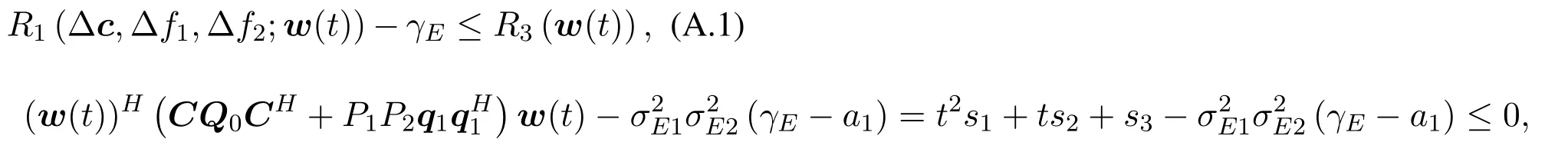
We will show that holds for any∥∆c∥2≤ ε,|∆fj| ≤ εj,j= 1,2.Then by requiringR3(w(t))≤0 we can deduce thatwk+1(t)satisfies(4c).

According tow(t)=wk+t(ˆwk+1−wk),(A.1)is reduced to:

where

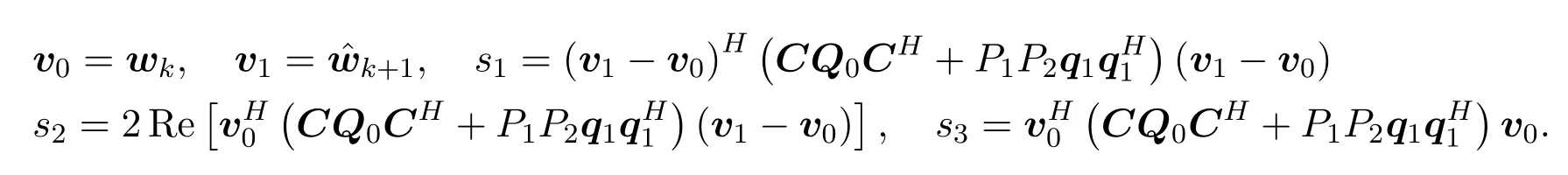
For any∥∆c∥2≤ε,|∆fj| ≤εj,j= 1,2,we have

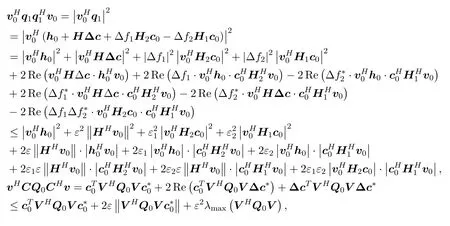
wherev=v1−v0andV=diag(v)Then

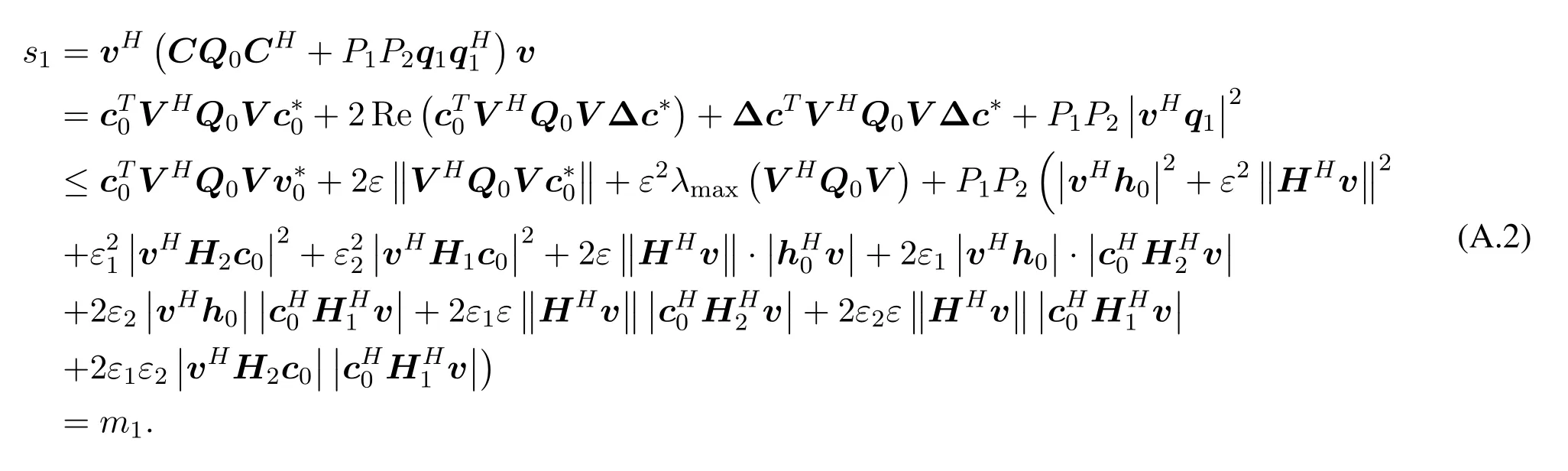
Similarly,we deduce that:

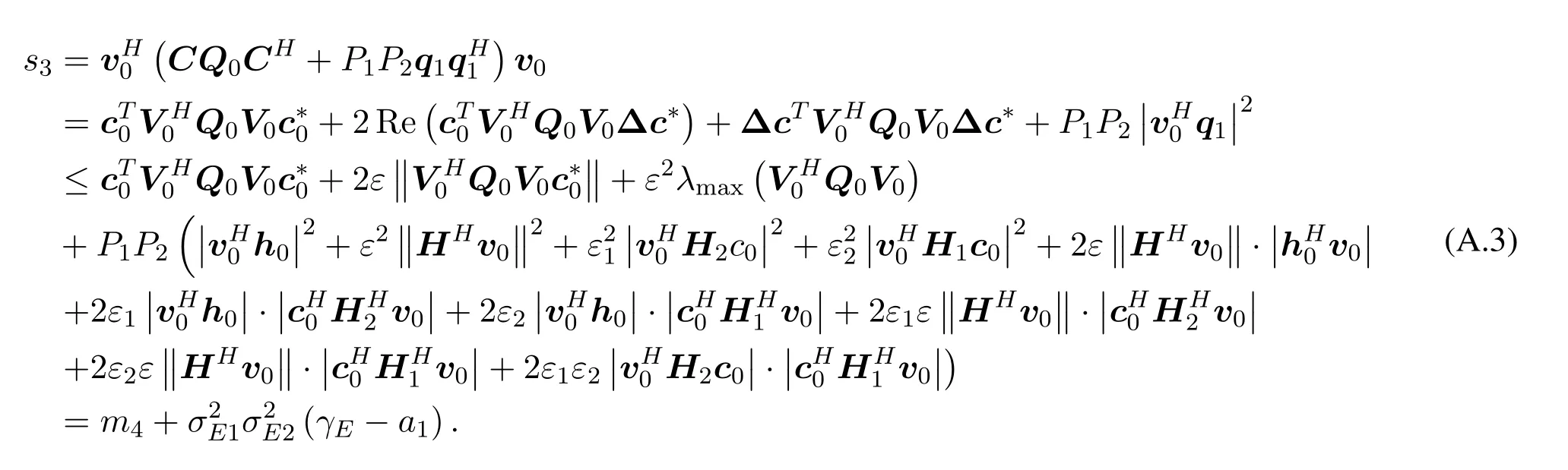
So

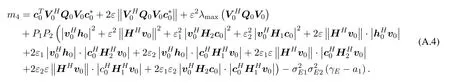
ts2is equivalent to the following form:

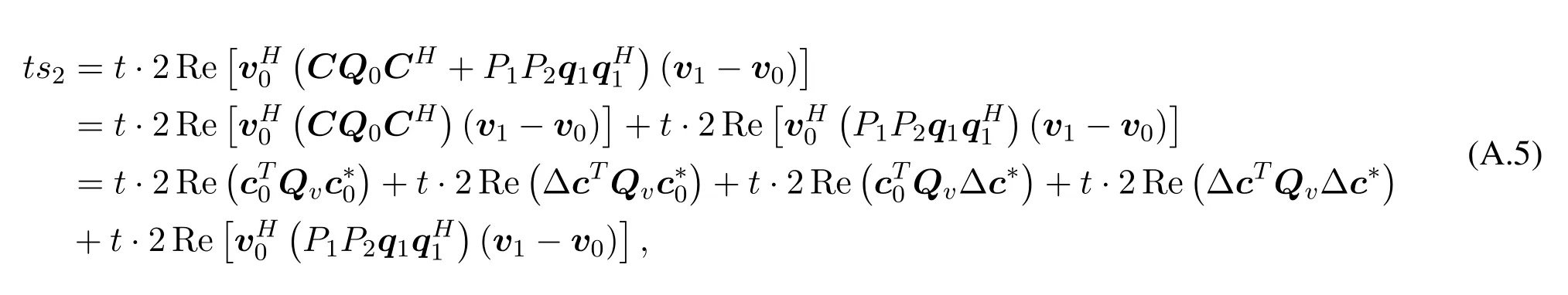
whereQv=0(V1−V0).The above equation can be deduced that:

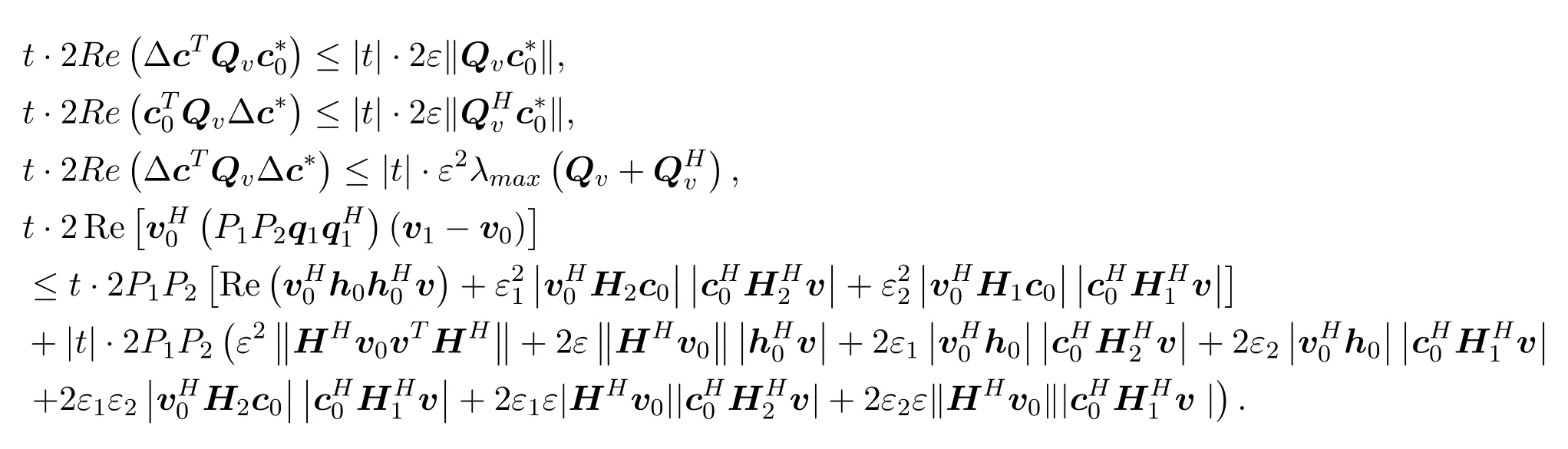
Thusts2≤tm2+|t|m3,where

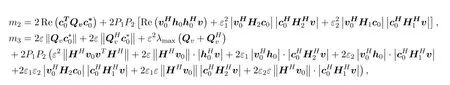
Now we find a upper bound ofR1:R3(w(t)) =t2m1+tm2+|t|m3+m4.Since the iteration pointwk+1(t)satisfies(12c),the following inequality holds:

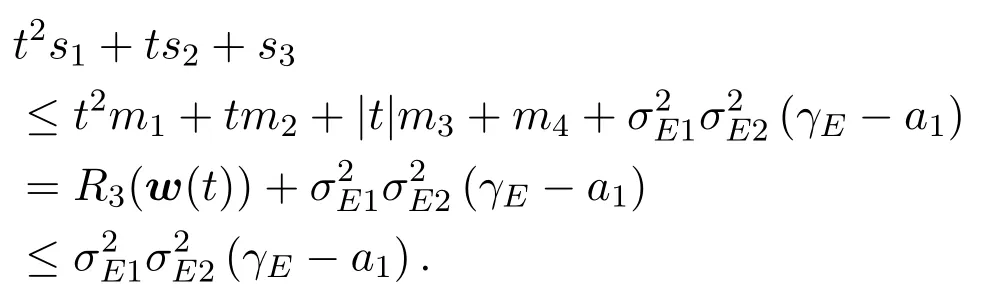
Thus

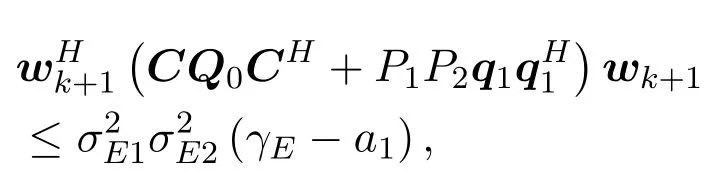
for all∥∆c∥2≤ε,|∆fj| ≤εj,j= 1,2.wk+1(t)satisfies (4c).This means thatwk+1(t) is a feasible point of problem(4a).Lettkbe the optimal solution of problem(12a),wk+1(tk)is a feasible point of problem(4a).

Becausetkis optimal solution of problem(12a),we havePR(wk+1(tk))≤PR(wk+1(0)), which meansPR(wk+1)≤PR(wk).In other words,the objective function of problem(4a)decreases monotonically.

Next, we provet= 0 is always a feasible solution of problem (12a).For the casek= 0,t= 0 meanswk+1(0) =w0.Asw0satisfies(5),we have thatt=0 satisfies(12b).Then

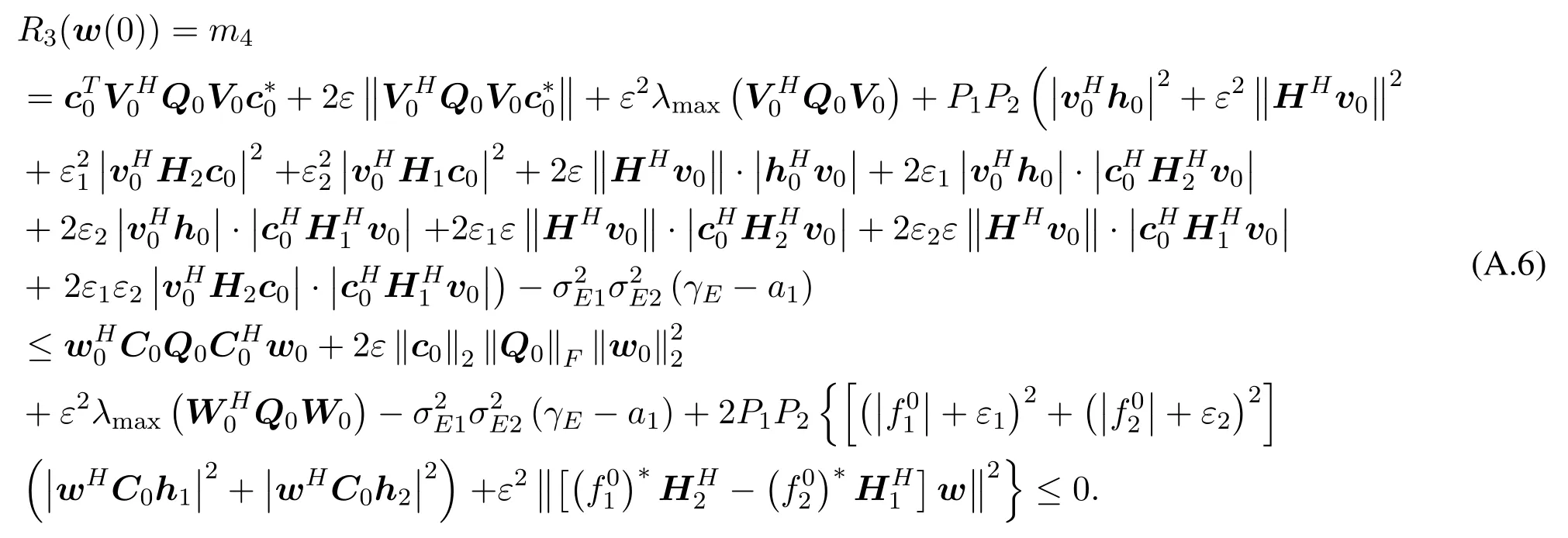
The last inequality comes from the last constraint of problem (5).(A.6) is equivalent toR3(w(0))(γE −a1).Thent= 0 satisfies(12c).t= 0 is the feasible point in initial iteration.

Whenk >0,t= 0 makeswk+1=wk.Sincewksatisfies(12b)and(12c),it is trivial to see thattk= 0 is the feasible solution of problem(12a).

From both cases we can conclude thatt= 0 is a feasible point of problem(12a).

APPENDIX B.PROOF OF THEOREM 2

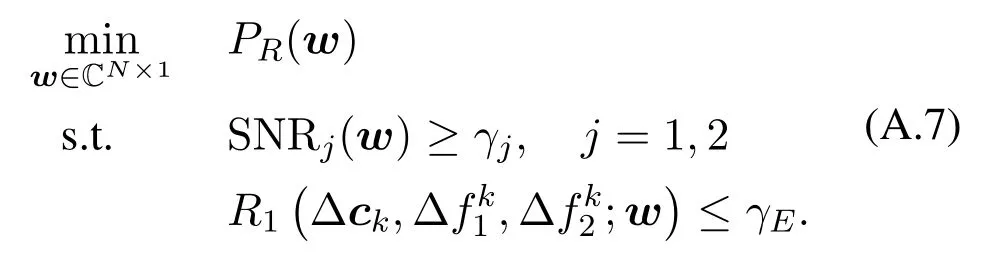
Supposewkis not the optimal solution of problem(4a).Denotew∗as another feasible point of (4a),andPR(w∗)≤PR(wk).There must exist ∆c∗and∆=1,2 such that

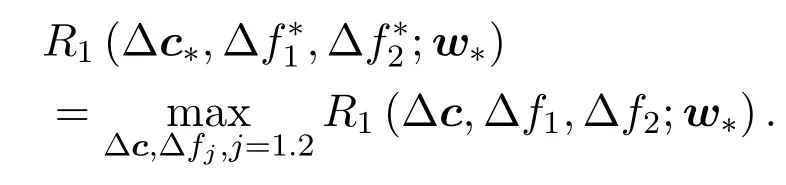
Obviously

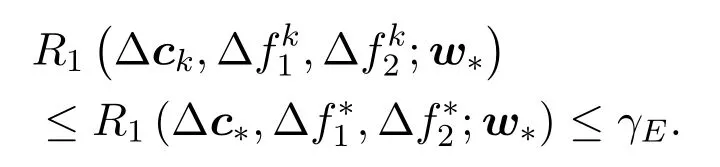
In this case,w∗is a feasible point of (A.7), and has a lower objective function value thanwk.This contradicts with the fact thatwkis optimal for problem(A.7).Thus the assumption does not hold.wkmust be the optimal solution of problem(4a).