Multi-Objective Bacterial Foraging Optimization Algorithm Based on Effective Area in Cognitive Emergency Communication Networks

Shibing Zhang,Xue Ji,Lili Guo,2,Zhihua Bao

1 School of Information Science and Technology,Nantong University,Nantong 226019,China

2 Xinglin College,Nantong University,Nantong 226008,China

Abstract: Cognitive emergency communication networks can meet the requirements of large capacity, high density and low delay in emergency communications.This paper analyzes the properties of emergency users in cognitive emergency communication networks, designs a multi-objective optimization and proposes a novel multi-objective bacterial foraging optimization algorithm based on effective area(MOBFO-EA)to maximize the transmission rate while maximizing the lifecycle of the network.In the algorithm,the effective area is proposed to prevent the algorithm from falling into a local optimum, and the diversity and uniformity of the Pareto-optimal solutions distributed in the effective area are used to evaluate the optimization algorithm.Then, the dynamic preservation is used to enhance the competitiveness of excellent individuals and the uniformity and diversity of the Pareto-optimal solutions in the effective area.Finally,the adaptive step size,adaptive moving direction and inertial weight are used to shorten the search time of bacteria and accelerate the optimization convergence.The simulation results show that the proposed MOBFO-EA algorithm improves the efficiency of the Pareto-optimal solutions by approximately 55%compared with the MOPSO algorithm and by approximately 60% compared with the MOBFO algorithm and has the fastest and smoothest convergence.

Keywords: wireless communications; emergency communications; cognitive radio networks; multiobjective optimization algorithm;effective areas;selfadaption

I.INTRODUCTION

Every year, there are lots of major natural disasters occurred in the world.If a serious natural disaster(such as an earthquake or a flood) or man-made disaster(such as a terrorist attack or major accident)occured,the stable and reliable high-speed data transmission and wireless multimedia communications such as voice, image, and live video stream between the emergency rescuers on-site would be very important for effective rescue and coordination.At the rescue site, rescuers, who might come from different countries or areas, would use various kinds of noninteractive communication devices,possibly resulting in difficulties in sharing the information among rescue teams, hospitals, and disaster area management agencies.The conventional communication networks with interactivity such as mobile communication networks would be vulnerable or would be overloaded because of the destruction of the infrastructure during the disasters.They would not be able to meet the requirement of the burst communication services with exponential growth in the emergent case[1].Private networks, such as satellite mobile communication networks, shortwave communication networks,would be very easily overloaded during the disasters and would be idle during the nonemergency communication[2,3].

An effective emergency communication network should not affect the existing licensed network under normal conditions[4–7]and have sufficient spectrum resources to ensure the communications and meet the emergency requirements for large capacity, high density and low delay communication services in the case of emergency.Cognitive radio (CR) technology has the ability to perceive its own environment, learning from its environment around, mine spectrum resources, and restructure the communication network.It has become widely favored in the research on nextgeneration wireless communications, such as sixth generation (6G), device to device communications(D2D),and end to end(e2e)communication networks[8–10].The characteristics of emergency communication networks,such as high reconfigurability,traffic burst, transmission reliability and coverage range, inspire us to explore the emergency communication network technology based on cognitive radios.

However,the existing solution for CR networks cannot be directly used in cognitive emergency communication networks.On the one hand,the delay-sensitive and fault-tolerant multimedia traffic is much more than the loss-sensitive and delay-tolerant download traffic in the cognitive emergency communication networks.Therefore, a novel cross-layer communication framework should be designed to optimize cognitive emergency communication networks globally, where the local interference constraints,the QoS requirements of the e2e service of the emergency network and the existing communication networks should be considered.On the other hand,the emergency users(i.e.secondary users) have priority to access the network to authorized users in the cognitive emergency networks.This kind of priority level varies based on the location,time and nature of the task.Therefore,cognitive emergency communication networks should change the primarysecondary role of the networks according to the dynamic rescue mission policy timely rather than using the existing fixed primary-secondary role model.

This paper designs a multi-objective optimization for cognitive emergency communication networks,that maximizes the transmission rate of emergency users while maximizing their lifecycle, and develops globally optimal solutions to meet the requirements for large capacity, high density and low delay in the networks.The main contributions are summarized as follows:

• We design a multi-objective optimization to meet the requirements for large capacity, high density and low delay in cognitive emergency communication networks.

• We propose a novel multi-objective bacterial foraging optimization algorithm based on effective area(MOBFO-EA)to achieve the multi-objective optimization.

• We propose the effective area, and use the diversity and uniformity of Pareto-optimal solutions distributed in the effective area to evaluate the optimization algorithms.This effectively prevents the algorithm from falling into a local optimum.

• We utilize dynamic preservation to enhance the competitiveness of excellent individuals and improve the uniformity and diversity of nondominated solutions in the effective area.

The rest of the paper is organized as follows.Section II.presents some related work.Section III.describes the optimization problem in cognitive emergency communication networks and designs the multiobjective optimization.The MOBFO-EA algorithm is proposed in Section IV.Section V.provides some simulation results to evaluate the algorithm.Finally,some conclusions are drawn in Section VI.

II.RELATED WORK

Usually, three kinds of approaches are used for multiple-objective optimization, namely taking the most important factor as the objective and the others as constraints [11], converting a multi-objective problem into a single objective problem with different weights for each objective [12], and finding the Pareto-optimal set that satisfy all objectives simultaneously[13].The first approach is useful in the cases where there exists a clear priority relationship between the different optimization objectives.The second approach is quite conducive for optimizing linear combination goals [14].However, it is often difficult to get accurate weighting coefficients due to the ambiguity of the practical environment and the constraints.The last approach is widely used to perform multiobjective optimization with conflicting objectives.

A genetic algorithm (GA) is a global random optimization algorithm that was developed by rigorously simulating the evolution mechanism of life [15], and the non-dominated sorting genetic algorithm(NSGA)is a genetic algorithm based on the Pareto-optimal that is often used to deal with multi-objective optimization problems[16].In 2002,Deb et al.improved the original NSGA and proposed a non-dominated sorting genetic algorithm with an elite strategy(Non-dominated Sorting Genetic Algorithm II,NSGA-II)[17].In[18],Wang et al.designed an improved NSGA-II using local simulated annealing (SA) operators with Unitedscenario neighborhood structure that can improve the flexibility in the face of the uncertainty described by scenarios.

In 2002,Passino proposed the bacterial foraging optimization(BFO)algorithm that is based on the foraging and reproduction behavior of E.coli [19].Compared with other organisms such as birds and fish,the structure and behavior of bacteria are simple, and the fast-paced lifecycle of the flora is more suitable for optimization simulation.Niu et al.improved the BFO algorithm and proposed a multi-objective bacterial foraging optimization (MBFO) algorithm to achieve multi-objective optimization,and the benchmark function has been tested for the two-objective practical problems [20].To deal with the multi-objective optimization problems, the Pareto-dominated mechanism was incorporated into particle swarm optimization(PSO)and the multiple objectives with particle swarm optimization(MOPSO)was proposed[21].It has been verified that the MOPSO algorithm has great competitive advantage in solving multi-objective optimization problems.In [22], Hafez proposed a multi-objective hybrid bacterial foraging particle swarm (MOBFPS)optimization for secure power system operation that combines the BFO algorithms with the particle swarm optimization(PSO)algorithms.This algorithm has the advantages of search diversity, fast convergence and solution quality.Tan et al.adopted a fitness survival mechanism to control the individuals chance of survival during the process of reproduction and elimination for the multi-objective economic-environmental dispatch problem in which a comprehensive learning strategy is employed to ensure fast convergence and avoid local optimum[23].

The evolution-based multi-objective heuristic optimization algorithms described above can solve the optimization problem of multiple conflicting objectives.However, the obtained solutions may easily fall into local optimum solutions.In this paper, we first designed the cross-layer multi-objective optimization for cognitive emergency communication networks, and then proposed a multi-objective bacterial foraging optimization algorithm that is based on effective area.We introduced the learning mechanism to the chemotaxis operation of the BFO algorithm to adaptively change the direction and step of the bacterial movement in our MOBFO-EA algorithm.To solve the contradiction between different optimization objectives,we proposed the effective area and use the diversity and uniformity of the Pareto-optimal solutions distributed in the effective area to evaluate the optimization algorithms.We use the non-dominant sorting and crowding distance mechanisms to find the global best position of the multi-objective optimization.Finally,we apply the fuzzy decision approach to calculate the membership of each individual, and selected the bacteria with the largest membership as the best compromise solution.

III.OPTIMIZATION IN COGNITIVE EMERGENCY COMMUNICATION NETWORKS

In cognitive emergency networks, spectrum access of an emergency user (EU) follows the variable primary-secondary mode instead of the fixed primarysecondary mode in general cognitive networks.When a serious disaster occurred, the characteristics of the rescue mission in different disaster areas would be different.The EUs in different disaster areas and traffic in different period should be assigned different priority.The priority of an EU should vary over space(from disaster center to periphery area)and time(from task scheduling to rescue, recovery, and evacuation) [24].Therefore,we divide the EUs in the network into three types of EUs according to the properties of the mission of EUs: extra urgent EUs, urgent EUs and ordinary EUs.The extra urgent EU has the highest priority and may access any subchannels regardless of whether a licensed user is present in the subchannel.The urgent EU has the higher priority and may access any subchannel if there is no harmful interference to authorized users.The ordinary EU can only access the idle subchannel.

Suppose there areLlicensed users (LUs) andVEUs in a cognitive emergency communication network withNsubchannels.ThevthEU (EUv),v=1,2,....,V, has data to be transmitted to the destinationd,as shown in Figure 1.Thenth,n=1,2,....,N,subchannel has the bandwidthBnand Gaussian noise with 0 mean andvariance.The optimization objective of the network is to maximize the e2e bit rate of the EUs while considering the mission policy of the network and the signal to interference plus noise ratio(SINR)of LUs.

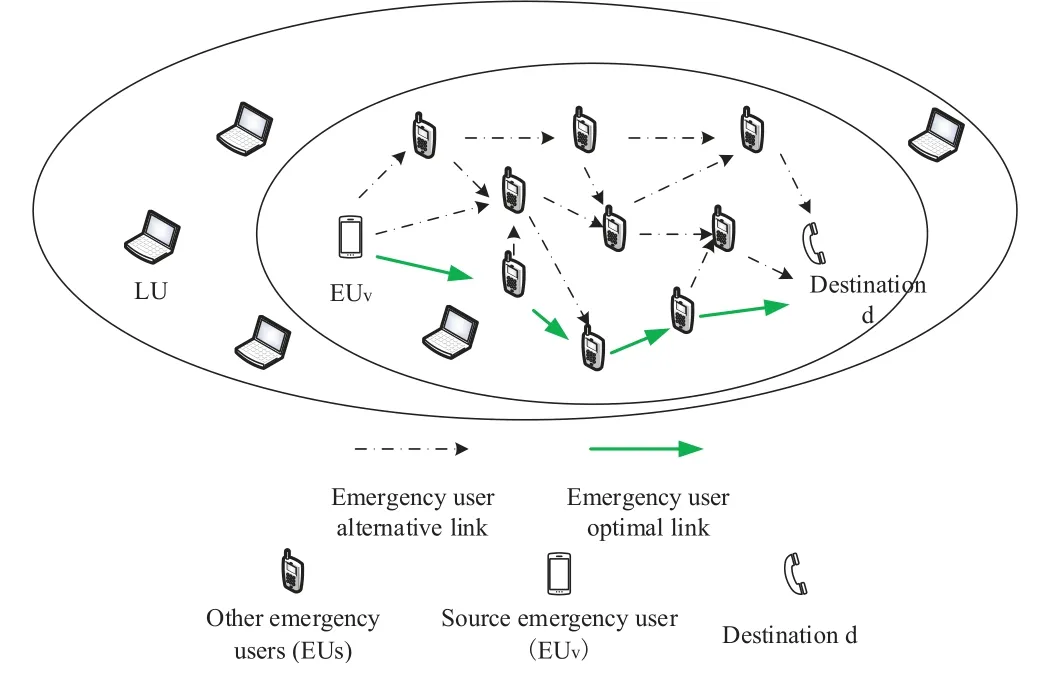
Figure 1. Model of cognitive emergency communication networks.

When an EU carries out an extra urgent mission, it has the absolute priority to access the spectrum regardless of whether LUs are present.In this case,the interference to the LU caused by the EU is not considered.Assume that the idle probability ofnthsubchannel isp0,the busy probability isp1,the transmitted power of EUvinnthsubchannel is,and the e2e power gain of EUs innthsubchannel ishSSn.The optimization objective of the cognitive emergency communication network is to maximize the transmission rate of thevthEU,Rv, in cognitive emergency communication networks as follows

where,Rv0is the transmission rate of EUvinnthsubchannel when it is idle;Rv1is the transmission rate of EUvinnthsubchannel when it is busy;=PPnhPSnis the interference of the LU to the EU innthsubchannel, which is only related to the transmitted power of the LU,PPn, and the interference gain,hPSn,between the LU and EU innthsubchannel; andQvis the maximum transmitted power allowed of EUv,anddenotes the constraint on the transmitted power of EUv.

When the EU performs an urgent mission, it will access the spectrum in the overlay mode or underlay mode without affecting the LU data transmission.If the EU accesses the spectrum in the underlay mode,it will interfere with the LU.Clearly, the interference power of EU to LU innthsubchannel,is only related to the transmitted power of the EUand channel interference gainhSPnbetween the EU and LU innthsubchannel as follows

At this time, the optimization goal of the network is to maximize the data transmission rate of the EU,Rn,under the premise of no interference with the data transmission of the LU as described by

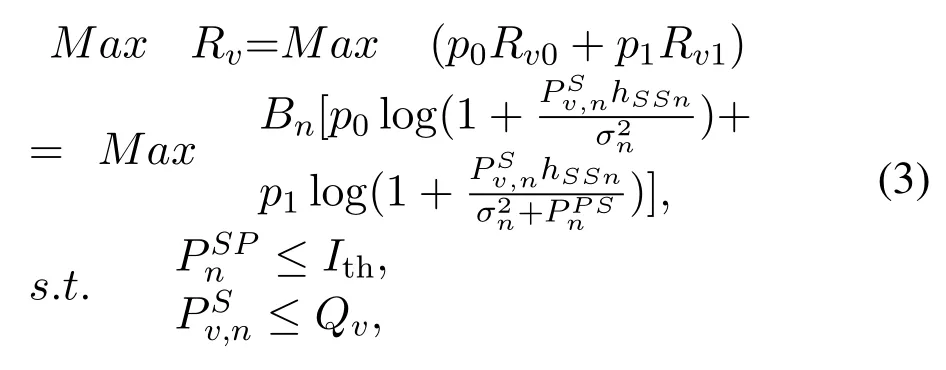
whereIthis the interference threshold that the LU can accept, and≤Ithdenotes the interference constraint of the EU to the LU.

In cognitive emergency communication networks,most EUs are mobile nodes,and their power supplies are mainly rechargeable batteries.however,it is difficult to charge mobile nodes at the disaster site.Maximizing the life cycle of the EUs network is another optimization objective of the network.We use the ratio of the transmitted power of the EUv,to the maximum transmitted power allowed of EUv,Qv, to evaluate the the lifecycle of the EUv,and the optimization goals in (1) and (3) become the multi-objective optimization with conflicting objectives as described by

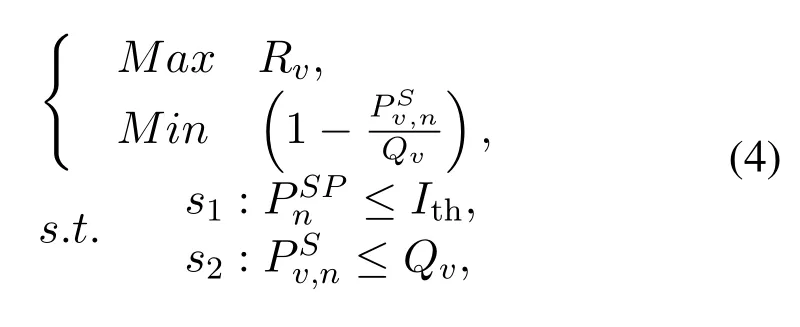
i.e., the optimization goal of the EUs is to maximize the transmission rate of the EUs while maximizing the lifecycle of the EUs network.The difference in the optimization goals between the extra urgent EUs and urgent EUs is whether to consider the constraint.For the convenience of optimization,the optimization objectives in (4) can be further represented as follows

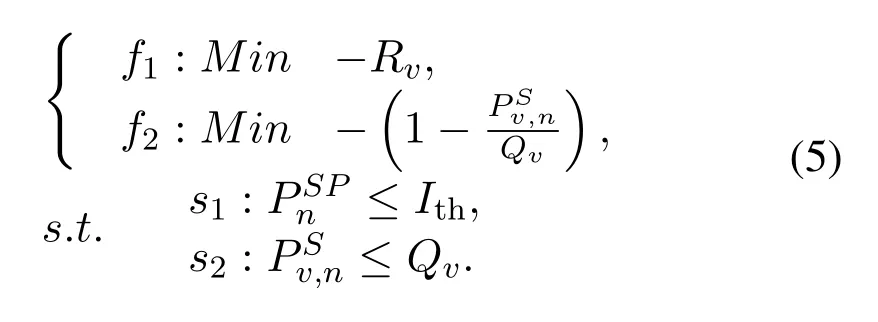
It is easy to prove that the optimization in (5) is a convex optimization.

Considering ordinary EUs, it is clear that they can only access an idle channel.In this case, the optimization is the same as that for common cognitive networks.There have been many solutions to solve the optimization[25,26],and we will not explore this optimization in this paper.

IV.MOBFO-EA ALGORITHM

In order to solve the optimization effectively,we proposed a novel MOBFO-EA algorithm based on BFO algorithm [19, 20].In the algorithm, the effective area is proposed to achieve the efficient Pareto-optimal solutions in the multi-objective optimization, the dynamic preservation is advanced to enhance the competitiveness of excellent individuals,the adaptive step size and moving direction are used to shorten the search time of the bacteria, and fuzzy decision is applied to obtain the global best compromise solution.The flow chart of the MOBFO-EA algorithm is shown in Figure 2.

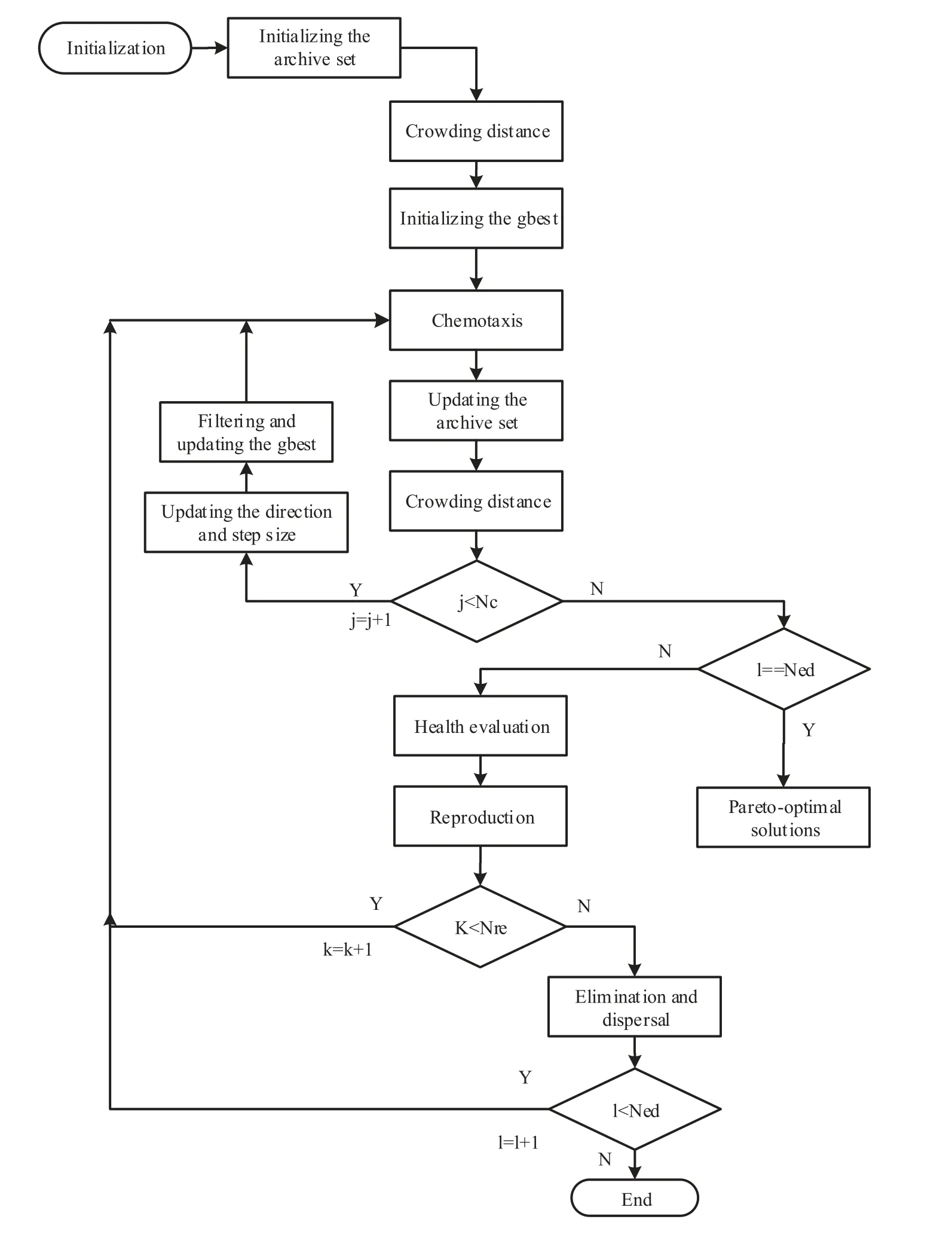
Figure 2. Flow chart of MOBFO-EA algorithm.

4.1 Adaptive Chemotactic Operation Step and Direction

The fixed step size and a random moving direction in the chemotactic operation of BFO algorithm may find the optimal solution in some simple optimization problems but are not suitable for complex optimization problems.In our MOBFO-EA Algorithm,we let bacteria adaptively adjust their step size and moving direction according to their own information, and combine the chemotaxis operation in the BFO algorithm with the learning mechanism in the PSO algorithm,in which the chemotaxis operation performs local search and the learning operation performs global search[27–30].

First, let the step size of each bacterium in the(j+1)thchemotaxis operation be dependent on the distance between the current position ofithbacterium and the global historical best position as follows

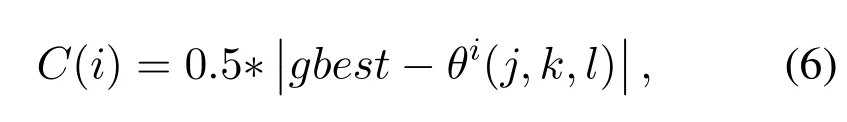
where,θi(j,k,l)is the position information ofithbacterium at thejthchemotaxis,kthreproduction andlthelimination-dispersal operation,gbestis the global historical best position.

Then, the position ofithbacterium in (j+1)thchemotaxis operation can be obtained by

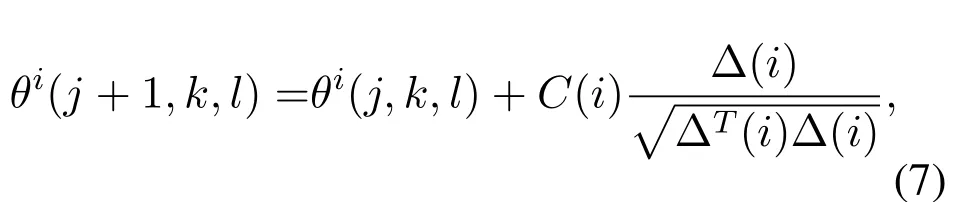
where ∆(i) is the direction vector ofithbacterium with the range[−1,1],Tdenotes the conjugation.

Finally,let the moving direction in(j+1)thchemotaxis operation ofithbacterium be related to its personal historical best position (denoted aspbest) and the global historical best positiongbestas follows

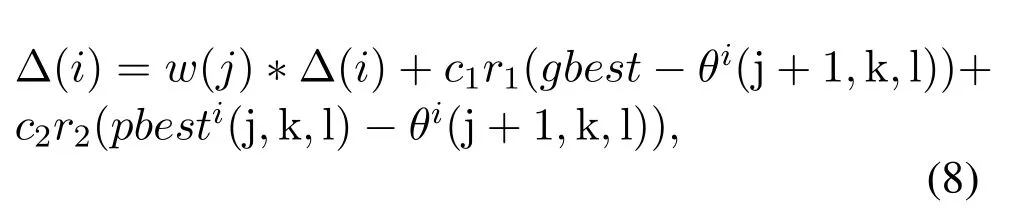
wherew(j) is the inertia weight,c1, andc2are the acceleration constants,c1≥0,c2≥0,andr1,andr2are random in[0,1].

Denoted the fitness values (of bacteriumibefore thejthchemotaxis operation asold,and the fitness values()after thejthchemotaxis operation asnew, the selection for the personal historical optimal positionpbestis shown in Algorithm 1.

In the update of the moving direction, the inertia weightw(j) denotes the ability of particles to inherit the previous moving direction.A larger inertia weight will be beneficial for the global search while a smaller weight will be beneficial for the local search[31,32].In our MOBFO-EA algorithm, we introduce the linearly decreasing inertia weightw(j)into the direction update in the chemotactic operation as follows

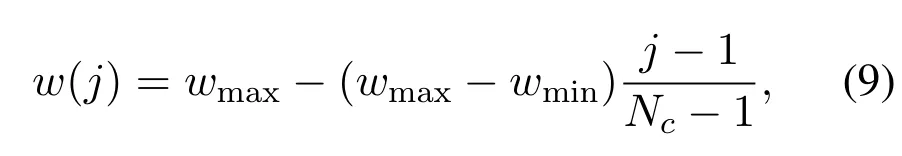
wherewmaxandwminare the upper and lower boundaries of the inertia weight respectively,Ncis the number of the chemotaxis operations.

Algorithm 1. pbest selection.1: Compare the fitness values(Ji1,Ji2)of bacterium i before and after the jth chemotaxis operation 2: if old dominates new then 3: pbest=old 4: else if new dominates old then 5: pbest=new 6: else if there is no dominant relationship between old and new then 7: the value of pbest chooses between new and old with a probability of 0.5 8: end if

This hybrid operations avoids the blindness in the search for the optimal options of bacteria, shortens the search time, and improves the convergence speed and search accuracy in the optimization.The adaptive chemotactic operation flow chart is shown in Figure 3.

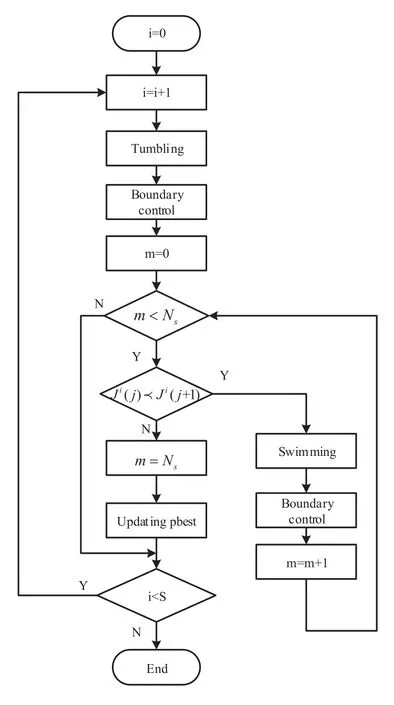
Figure 3. Chemotaxis operation in MOBFO-EA algorithm.

4.2 Effective Area of Solutions

4.2.1 Definition of Effective Area Generally, there is a contradiction between the objectives in the multi-objective heuristic optimizations.Considering the diversity of optimal solutions for the optimization objectivesf1andf2, we use the diversity and uniformity of the Pareto-optimal set obtained in the entire search area to evaluate the optimization algorithm.The optimization objectives in formula(5)can be summarized as that the lifecycle of the EU networks should be maximized while the transmission rate of EUs is maximized.It means that the area with a low EU transmission rate or a short lifecycle in the search area will not be considered in the optimization objectives.

We define the area withinJ1min≤ J1≤J1max,J2min≤J2≤J2maxas the search area and denote the Pareto-optimal set distributed in the search area asarchive1, define the area withinJ1min≤J1≤a,J2min≤J2≤b2as the effective area and denote the Pareto-optimal set distributed in the effective area asarchive2.In order to make the obtained Pareto-optimal solution spread over the entire effective area,or to make the EU transmission rate as large as possible, we define the area withinJ1min≤J1≤a,J2min≤J2≤b1(b1≤b2)as the filtering area and denote the Pareto-optimal set distributed in the filtering area asarchive3,as shown in Figure 4,whereJ1andJ2correspond to the values of functionsf1andf2in (5) respectively, and the search area is larger than the effective area, and the effective area is a slightly larger than the filtering area.Therefore,the goal of our MOBFO-EA algorithm is to make the Pareto-optima solutions concentrated and distributed uniformly in the effective area.

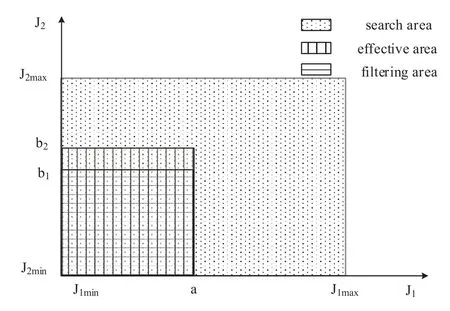
Figure 4. Area distribution of the Pareto-optimal solutions.

The ranges defined of the effective area and the filtering area will affect the selection ofgbestand the distribution of the final obtained Pareto-optimal solution set.If the effective area and the filtering area are set too large, the Pareto-optimal solution set obtained by the algorithm will not meet the requirements of emergency communication networks; if the effective area and the filtering area are too small, the solutions obtained by the algorithm will easily fall into the local optimum.Considering of the complexity of the practical application scenarios, the ranges of the effective area and filtering area should be determined according to the requirements of emergency communication networks.

4.2.2 Selection ofgbest

If a bacterium is dominated by other bacterias, it will lose its competitiveness in foraging and should be replaced by other individuals or should learn from other better individuals to survive.In our algorithm, we use the non-dominated sorting and crowded distance to achieve multi-objective optimization[16,17].After each chemotactic iteration,we rank the entire population with non-dominated sorting to obtain the Paretooptimal solution setarchive1,in which it is impossible to find the two function values of an individual are better than those of another individual simultaneously.Then,we calculate the crowding distance of each particle in thearchive1.The dominated solutions and non-dominated solutions are shown in Figure 5, and the selection method ofgbestis summarized as follows:

Figure 5. Dominated solutions and non-dominated solutions.

1.Ranking the entire population with nondominated sorting to obtainarchive1 after a chemotaxis movement.

2.Calculating the crowding distance of each bacterium inarchive1 and sortarchive1 in descending order of the crowding distance.The crowding distance of the first and last individuals inarchive1 is set to infinite.

3.Filteringarchive1 to obtain setarchive3 according to the fitness values of each bacteria,(j,k,l),(t=1,2).

4.Randomly selecting a bacterium from thegbestpoolthat consists of the top 10% of individuals with the largest crowding distance inarchive3,asgbest.

4.2.3 Boundary Control in Chemotaxis

For multi-objective optimization,the control of the individual boundary is particularly important.Generally, there are two ways to control individuals.The first is to let the outgoing individuals stay at the boundary and change their forward direction to be added to the next iteration,and the second is to randomly generate new individuals (θmin≤θi(j,k,l)≤θmax) in the feasible area to replace the outgoing individuals,whereθmaxandθminare the upper and lower boundaries,as shown in Figure 6.

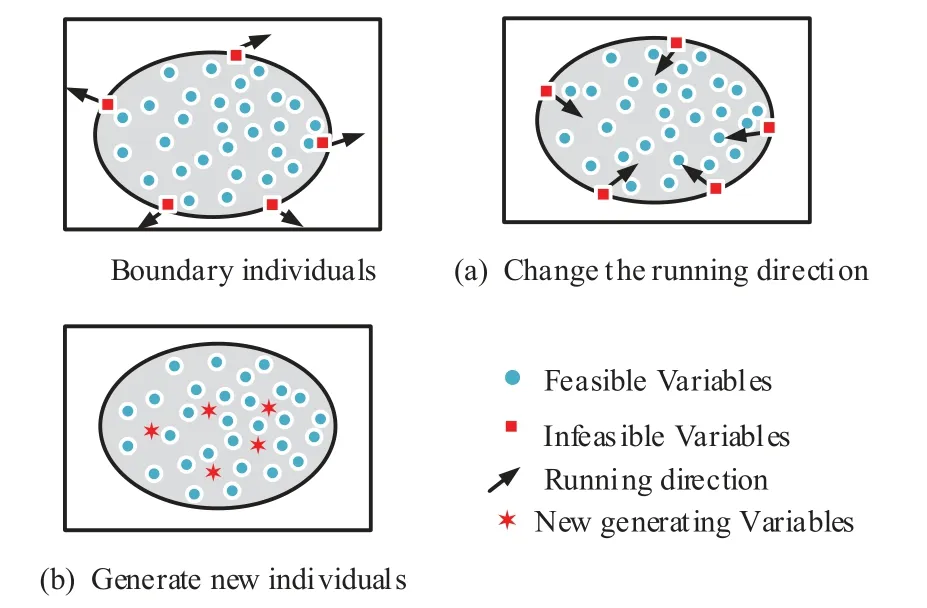
Figure 6. Two methods of boundary control.

Algorithm 2. Boundary control.1: if rand ≤Pr then 2: θi(j,k,l)=θmin(θmax)3: ∆(i)=−∆(i)4: θi(j+1,k,l)=θi(j,k,l)+C(i) ∆(i)√∆T(i)∆(i)5: else if rand>Pr then 6: θi(j+1,k,l)=θmin+rand ∗(θmax −θmin)7: end if

The first can spread the search area throughout the entire area,while the second is conducive to randomly generate new individuals to participate in next chemotaxis cycle, which increases the diversity of the individuals in the population.We combine these two boundary control ways in our algorithm.Suppose the bacteriaiis on the edge of the feasible area,the boundary control of the bacteria is shown in Algorithm 2,whererandis a random number in[0,1],Pris a fixed probability that indicates whether the first or second way is preferred.If we prefer the first one,Pr >0.5;if we prefer the second one,Pr ≤0.5.In the MOBFOEA algorithm, we prefer to use the first one to deal with the individuals to enhance the ability of the algorithm to explore boundary values.Thus, the uniformity and diversity ofarchive2 in the effective area can be further improved.

4.2.4 Dynamic Preservation Ratio in Reproduction

After a round of chemotaxis operations, the reproduction operation of bacteria is performed following the principle of ‘survival of the fittest’ based on their chemotaxis ability that is evaluated with the health index.The health index of theithbacterium at thekthreproduction andlthelimination,is the cumulative sum of the function values in the chemotaxis cycle described as follows[23]

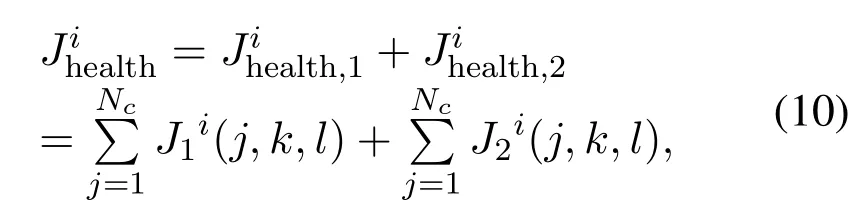
whereJti(j,k,l) is the fitness value of theithbacterium corresponding to thetth,t=1,2,optimization function at thejthchemotaxis,kthreproduction andlthelimination-dispersal operation,which are equal to the values of functionsf1andf2in formula (5), respectively.

Then,the bacteria are sorted in ascending order according to the bacterial health indices.The bacteria with lower health indices (notice that the health indices are negative) are preserved and reproduced to produce new offspring.Individuals with betterorare preserved to ensure the colony diversity and exploration of boundary solutions in the feasible area.We useto select the top(50%−p(k))individuals from the population to form population 1(marked aspop1)for objectivef1, useto select the topp(k)individuals from the population to form population 2 (marked aspop2) for objectivef2, and useto select the top 50% individuals from the population to form population 3 (marked aspop3),as shown in Figure 7.Then,the new population is made ofpop1,pop2andpop3.

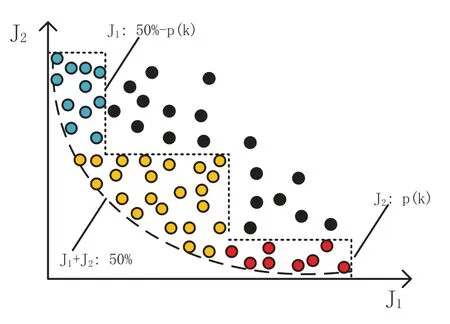
Figure 7. New population composition based on dynamic preservation ratio.

We note thatp(k)=λ1∗exp(−(k/Nre)∗λ2),whereNreis the number of the reproductive steps.The coefficientλ2is adjusted to control the change rate of the preservation ratio,the coefficientsλ1together withλ2are adjusted to ensure thatp(k)is 0.25 when the number of reproductionk=1.i.e.,when the first round of reproduction is performed,the health indicesandare equally important in the construction of a new population.It will be beneficial for ensuring the diversity of the colony.As the number of reproductionkincreases, the value ofp(k) decreases and the(50%−p(k))value increases.In cognitive emergency communication networks,the objectivesf1andf2are contradictory.For a given individual,a goodf1means a poorf2.An higher number of individuals with goodf1retained to participate in the next round of chemotaxis cycles means a greater ability of the population to explore the boundary value off1.This will result in the better diversity and uniformity off1in the archive set in the search area.

The renewal of bacteria based on the dynamic preservation ratio is summarized as follows:

4.3 Best Compromise Solution

In the practical cognitive emergency communication network, it is difficult to know the exact weight ratio between the different objectives.In some cases, we may need the best compromise solution to meet diverse optimization needs.To select the best compromise solution from the Pareto-optimal setarchive2 distributed in the effective area,we introduce the fuzzy decision[33]into our MOBFO-EA algorithm,i.e.,an optimal individual is selected from the decision domain according to certain fuzzy constraints.We define the membership function as follows

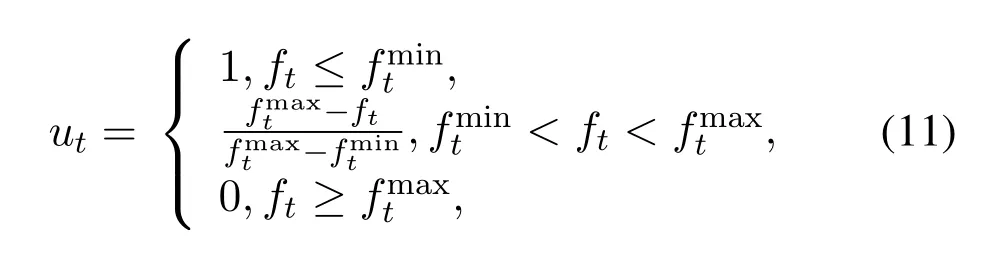
whereandre the predefined maximum and minimum values oftthobjective function,respectively.Then, the normalized membership function of themthnon-dominated solution in the effective area is obtained by

whereMis the number of the non-dominated solutions in the effective area,and the individual with the maximumumis the best compromise solution.

4.4 MOBFO-EA Algorithm Proposed

If we take the fitness values of each bacterium(j,k,l)as the values of the optimization objectivesftin(5),take the location of a bacterium as the power transmitted ofEUv,and take the best compromise solution as the optimal solution of the optimization objectives, the MOBFO-EA algorithm proposed for the cognitive emergency communication networks can be summarized in Algorithm 3.

Algorithm 3 MOBFO −EA algorithm.1: Initialization 2: [Step 1] Initialize and randomly generate the direction vector ∆(i) of each bacterium i with the range[-1,1].3: [Step 2] Compute the fitness values of each bacterium i based on their position θi(j,k,l),Ji1(j,k,l)and Ji2(j,k,l),according to Eq.(5)respectively.4: [Step 3] Initialize the external solution set in archive1 according to the non-dominated solutions selected in Figure 5 and calculate the crowding distance of each bacterium.5: [Step 4] Initialize the gbest according to the selection method mentioned in subsection 4.2.2.6: Main loop 7: [Step 5]Elimination-dispersal loop: l=l+1 8: [Step 6]Reproduction loop: k =k+1 9: [Step 7]Chemotaxis loop: j =j+1 10: [7a] For i = 1,2,...,S, make the chemotactic step for the bacterium i as follows:11: [7b] Compute the step size C(i) of the bacterium i using Eq.(6).12: [7c] Compute the fitness values of the bacterium i, Ji1(j,k,l) and Ji2(j,k,l) respectively,corresponding to its position θi(j,k,l).13: [7d] Let Jlast1 = Ji1(j,k,l), Jlast2 =Ji2(j,k,l);

?

?

V.NUMERICAL RESULTS AND DISCUSSION

In this section, we simulate the MOBFO-EA algorithm in extra urgent and urgent cases and compare it with the MOBFO and MOPSO algorithms[20,21].The simulating parameters of the cognitive emergency communication network are given in Table 1, where the Gaussian noise powervaries randomly between[10−9,10−8]W,the e2e power gain of EUs innthsubchannelhSSnvaries randomly between [0.5,1]; and the simulation parameters of the MOBFO-EA algorithm are given in Table 2.According to the parameter settings in the emergency communication network and the range of Pareto-optimal solutions obtained after iterations,the effective area is set asf1<=−14&f2<=−0.6,and the filtering area is set asf1<=−14&f2<=−0.65 in this simulation.

Table 1. Simulation parameters of cognitive emergency communication networks.

Table 2. Simulation parameters of the MOBFO-EA algorithm.

Moreover, the fixed step size in MOBFO is set to 0.1 and thePris set to 0.5; the other parameters in MOBFO are the same as those in MOBFO-EA.Thec1andc2parameters in the MOPSO algorithm are both set to 2, and the maximum number of iterations in MOPSO is 2000.

5.1 Extra Urgent Case

In the extra urgent case, emergency users have absolute spectrum access priority.As long as emergency users want to access the subchannel, they can access any spectrum in the cognitive emergency communication networks.

Figure 8 show the uniformity and diversity of the Pareto-optimal solution setsarchive1 obtained with the MOBFO-EA, MOBFO and MOPSO algorithms in the search area, respectively.Although the best comprise solutions of the three algorithms are approximate, the Pareto-optimal solutions achieved by the MOBFO-EA algorithm are much more concentrated in the effective areaf1<=−14&f2<=−0.6 compared with the MOBFO and MOPSO algorithms.This means that the effectiveness of the Pareto-optimal solutions obtained with the MOBFO-EA algorithm are much higher than those obtained with the other two algorithms.

Figure 8. Pareto-optimal sets obtained by three algorithms under extra urgent case.(a) MOBFO-EA; (b) MOBFO; (c)MOPSO;(d)comparison of three algorithms.

To further verify the concentration of the Paretooptimal solutions in the MOBFO-EA algorithm, Table 3 gives the average numbers of solutions inarchive1 andarchive2 and the ratios of the numbers of solutions inarchive2 to the numbers of solutions inarchive1 with the different algorithms.Compared with the MOPSO algorithm, the MOBFO-EA algorithm improves the ratio from 38.65%to 61.18%;compared with the MOBFO algorithm, the MOBFOEA algorithm improves the ratio from 37.59% to 61.18%.It is clear that the Pareto-optimal solutions inarchive1 obtained by the MOBFO-EA algorithm are more concentrated in the effective area,and greatly improve the efficiency of the optimization of cognitive emergency communication networks

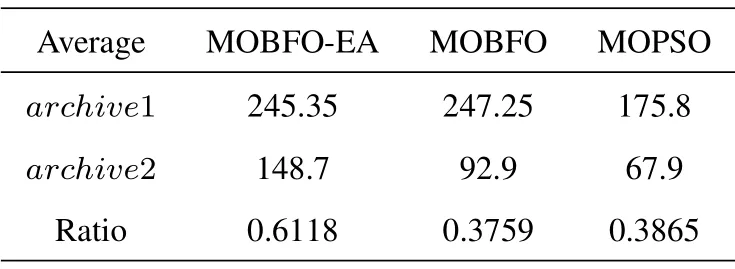
Table 3. Average distribution of archive2/archive1 in extra urgent case.

5.2 Urgent Case

In the urgent case,emergency users have spectrum access priority as long as their use of the spectrum does not cause harmful interference to licensed users.In this case, the optimization objective is the same as the extra urgent case except that the EU transmitting power is limited by the interference threshold of LUs.

Figure 9 illustrate the uniformity and diversity of the Pareto-optimal solution setsarchive1 obtained with the MOBFO-EA,MOBFO and MOPSO algorithms in the search area, respectively.Similar to the extra urgent case,the Pareto-optimal solutions achieved by the MOBFO-EA algorithm are much more concentrated in the effective areaf1<=−14&f2<=−0.6 than those obtained by the other two algorithm.This means that the MOBFO-EA algorithm has the highest efficiency in multi-objective optimization.

Table 4 gives the average numbers of solutions inarchive1 andarchive2 and thearchive2/archive1ratios obtained with the MOBFO-EA, MOBFO and MOPSO algorithms.Compared with the MOPSO algorithm, the MOBFO-EA algorithm increases the ratio from 42.99% to 64.68%; compared with the MOBFO algorithm, the MOBFO-EA algorithm increases the ratio from 40.04%to 64.68%.The concentration of the Pareto-optimal solutions in the effective area with the MOBFO-EA algorithm is much higher than ones with the other two,which is consistent with the conclusion in the case of extra urgency.

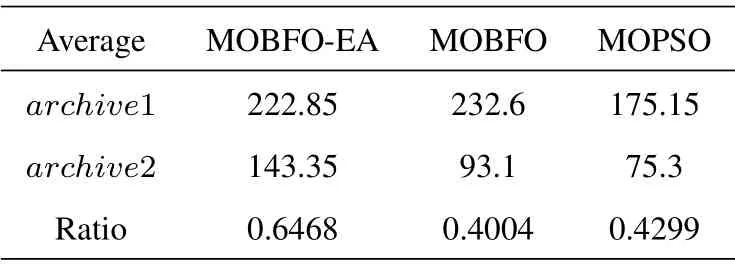
Table 4. Average distribution of archive2/archive1 in the urgent case.

5.3 Convergence Analysis

The generation distance (GD) is a common convergence index that can indicate the approximation of Pareto-optimal solution set to the true Pareto front[34].A smallerGDmeans that the obtained Paretooptimal solution set is closer to the true Pareto front and indicates a better convergence of the algorithm.SupposePdenotes the solution set obtained by the algorithm,P∗denote the true Pareto front,dis(x) denotes the minimum Euclidean distance between the pointxin the solution setPand the points in the true Pareto frontP∗,thenGDcan be given by

whereNPis the number of points in the solution setP.

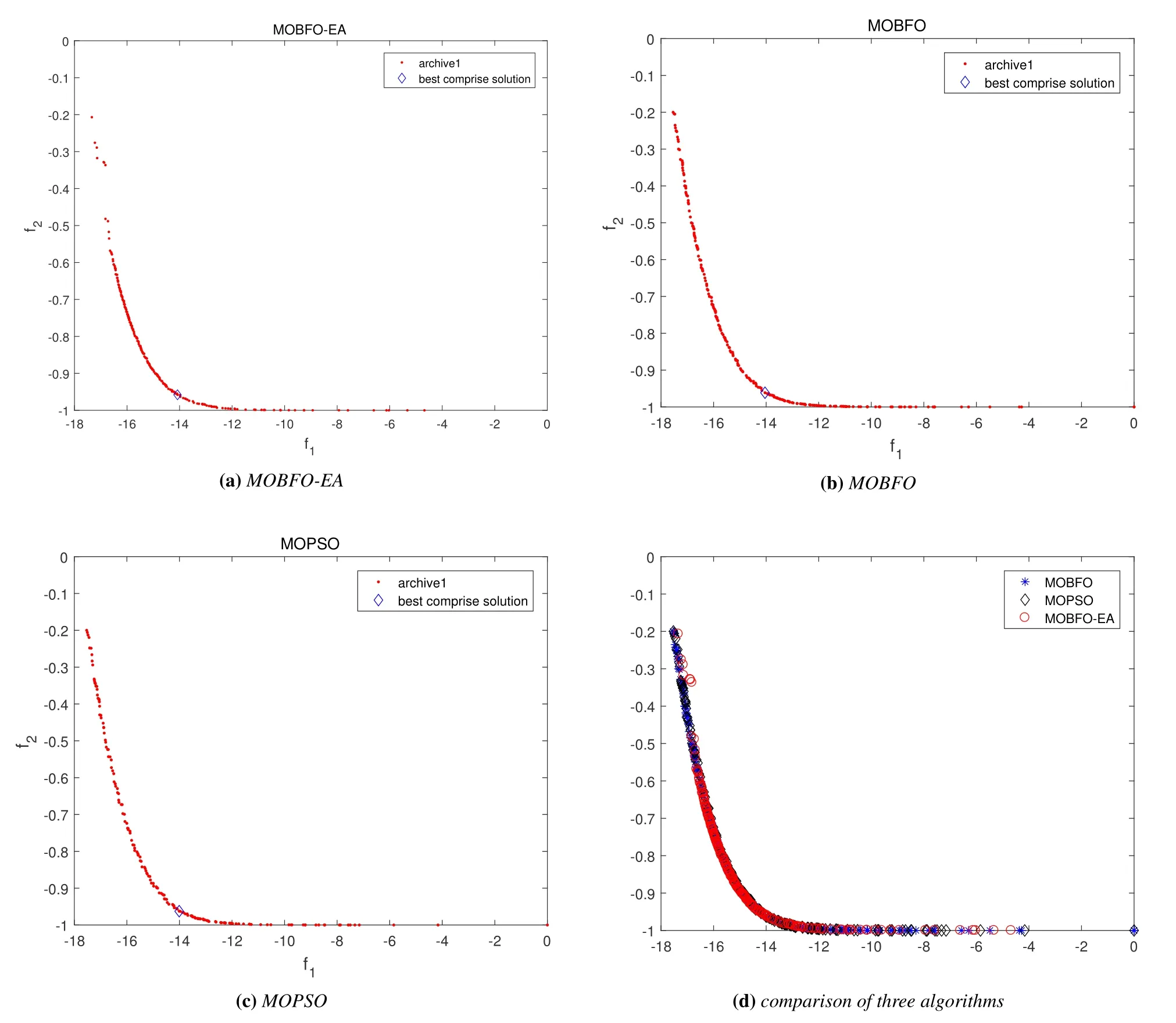
Figure 9. Pareto-optimal sets obtained by three algorithms under urgent case.(a)MOBFO-EA;(b)MOBFO;(c)MOPSO;(d)comparison of three algorithms.

In the MOBFO-EA and MOBFO algorithms, we calculate theGDafter each chemotaxis operation; in the MOPSO algorithm,we calculate theGDafter each iteration.Since the true Pareto front of actual problems is difficult to obtain, we refer to reference [35]to achieve the approximate Pareto front.We run the MOBFO-EA,MOBFO and MOPSO algorithms independently 20 times to obtain 60 Pareto-optimal solution sets in the entire area.Then, we rank the 60 solution sets with non-dominated sorting and obtain the Pareto solution set that is taken as the approximate Pareto front.

Figure 10 shows the convergence comparison of the three algorithms in terms of theGDmetric in the extra urgent and urgent cases, respectively.The smaller the GD value, the closer the non-dominated solution set obtained by the algorithm to the approximate front,which means a better convergence performance.Clearly,the MOBFO-EA algorithm shows the fastest and smoothest convergence,and has the highest convergence accuracy, while the MOPSO algorithm has poor convergence.

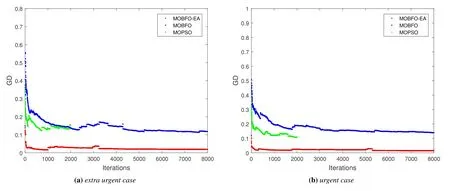
Figure 10. Convergence comparison of the algorithms under two cases.(a)extra urgent case;(b)urgent case.

VI.CONCLUSION

In this paper, we have designed the multi-objective optimization for cognitive emergency communication networks according to the properties of emergency users, and proposed the MOBFO-EA algorithm to achieve the Pareto-optimal solutions.We have proposed the effective area and use the diversity and uniformity of the Pareto-optimal solutions distributed in the effective area to evaluate the optimization algorithm, made use of the dynamic preservation to improve the competitiveness of excellent individuals and applied the adaptive step size, adaptive moving direction and inertial weight to improve the convergence.This solves the problem posed by the contradiction between the different optimization objectives,prevents the algorithm from falling into the local optimum and improves the uniformity and diversity of the Pareto-optimal solution sets in the effective area.Compared with the MOPSO and MOBFO algorithms,the concentration of the Pareto-optimal solutions obtained by the MOBFO-EA algorithm in the effective area is increased by approximately 55% and 60%,respectively.The MOBFO-EA algorithm shows the fastest and smoothest convergence.The MOBFO-EA algorithm is much more effective to solve the multiobjective optimization with conflicting objectives.

APPENDIX

Here is the proof of convex optimization.

For the convenience of proof of the convex optimization in the optimization problem (5), the optimization goals are represented as follows

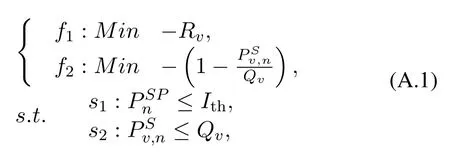
where,there is one restriction condition,s2,in the extra urgent case,and two restriction conditions,s1ands2,in the urgent case.

From (A.1), we obtain the first derivative off1toas follows

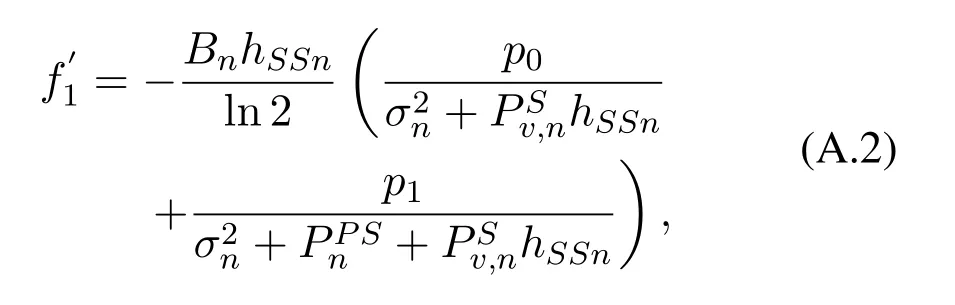
and the second derivative as follows

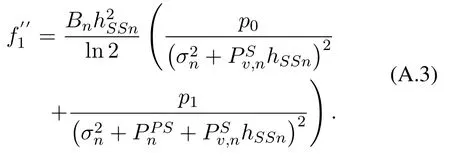
Obviously,0 and0.Because the restriction conditionss1ands2are both linear weightings and are larger than 0.Therefore, the functionf1is a convex optimization and there is an optimal solution inf1.Forf2,it is evident that there is an optimal solution becausef2is a monotonically increasing function.

Now, we weight the two optimization objectives withα(0<α<1) and (1−α) respectively, and combine them into a new function,F,as follows

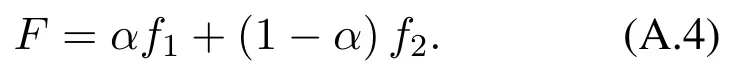
The first derivative ofFis given by

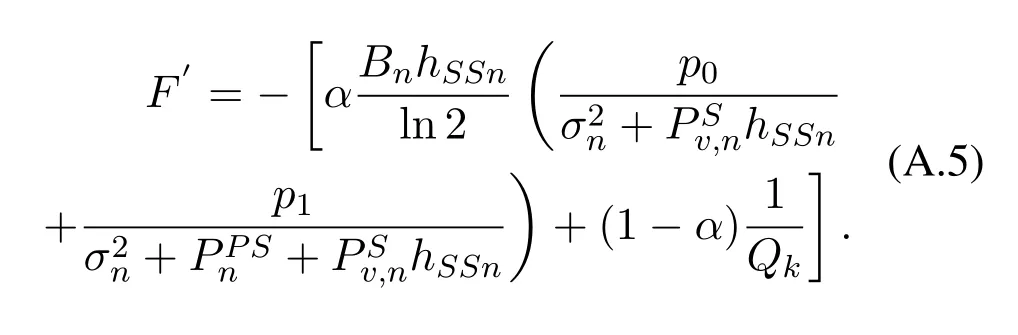
The second derivative ofFcan be expressed as follows

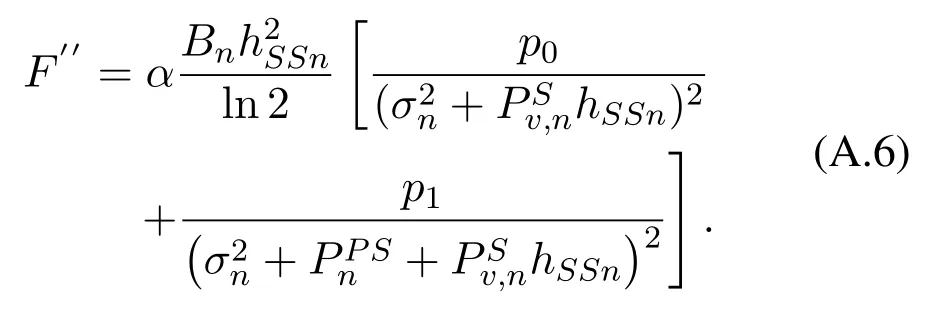
For anyα(0<α<1),we have

and

For the same reason as the constraint conditionss1ands2mentioned above, the functionFis a convex optimization and there is an optimal solution.

Therefore,the problem(A.1)is strictly a convex optimization problem.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China(Grant Nos.61871241 and 61771263) and Science and Technology Program of Nantong(Grant No.JC2019117).