Proactive Spectrum Monitoring for Suspicious Wireless Powered Communications in Dynamic Spectrum Sharing Networks
Yu Zhang,Guojie Hu,Yueming Cai
1 College of Communications Engineering,Army of Engineering University,Nanjing 210007,China
2 Sixtythird Research Institute,National University of Defense Technology,Nanjing 210007,China
3 Rocket Force University of Engineering,Xi’an 710025,China
Abstract: This paper studies the proactive spectrum monitoring with one half-duplex spectrum monitor(SM)to cope with the potential suspicious wireless powered communications (SWPC) in dynamic spectrum sharing networks.The jamming-assisted spectrum monitoring scheme via spectrum monitoring data(SMD)transmission is proposed to maximize the sum ergodic monitoring rate at SM.In SWPC, the suspicious communications of each data block occupy multiple independent blocks, with a block dedicated to the wireless energy transfer by the energy-constrained suspicious nodes with locations in a same cluster(symmetric scene)or randomly distributed(asymmetric scene) and the remaining blocks used for the information transmission from suspicious transmitters(STs) to suspicious destination (SD).For the symmetric scene, with a given number of blocks for SMD transmission,namely the jamming operation,we first reveal that SM should transmit SMD signal(jam the SD) with tolerable maximum power in the given blocks.The perceived suspicious signal power at SM could be maximized,and thus so does the corresponding sum ergodic monitoring rate.Then, we further reveal one fundamental trade-off in deciding the optimal number of given blocks for SMD transmission.For the asymmetric scene, a low-complexity greedy block selection scheme is proposed to guarantee the optimal performance.Simulation results show that the jamming-assisted spectrum monitoring schemes via SMD transmission achieve much better performance than conventional passive spectrum monitoring,since the proposed schemes can obtain more accurate and effective spectrum characteristic parameters,which provide basic support for fine-grained spectrum management and a solution for spectrum security in dynamic spectrum sharing network.
Keywords: proactive spectrum monitoring; sum ergodic monitoring rate; jamming-assisted proactive spectrum monitoring;half-duplex;fundamental tradeoff;dynamic spectrum sharing network
I.INTRODUCTION
1.1 Background
With the explosive data growth in wireless traffic,the shortage of spectrum resources is becoming more and more serious.How to improve the efficiency of spectrum utilization has been a hot issue in academia and industry.Spectrum management will play an important role in the next generation wireless network and will face increasingly challenges.Due to that dynamic spectrum sharing firstly shares the idle authorized spectrum for other legitimate users and can improve spectrum utilization by maneuvering in time domain, spatial domain, frequency domain and energy domain, it is considered as one of the key technologies to solve the problem of spectrum resource shortage in the future.Due to the openness of spectrum access mechanism of dynamic spectrum sharing and the broadcast nature of wireless communications, it is easy for illegal users to eavesdrop the spectrum information between the spectrum management node and legitimate users, and access spectrum illegally.Meanwhile,selfish legitimate users may also illegally use spectrum for greater benefits, such as transmitting signals in unauthorized time or space, and modifying spectrum technical parameters to obtain better transmission performance.Compared with traditional static spectrum allocation and access methods, dynamic spectrum sharing faces more serious spectrum security problems.Fine-grained spectrum management is considered as the key part to ensure spectrum security in dynamic spectrum sharing network (DSSN), which is implemented by confirming the spectrum identity of suspicious transmitters(STs)timely and accurately.There are some research results about spectrum identity recognition such as radio frequency fingerprint [1], emitter identification [2] and spectrum watermark[3],in which spectrum identity information will be transmitted with the transmission of the communication signal of STs.When the spectrum monitor(SM)finds ST in the process of routine spectrum monitoring,special spectrum monitoring will be started to further confirm the spectrum identity of the ST and the spectrum identity information of the ST will be extracted based on the detection and demodulation of the communication signal of STs.
1.2 Technical Literature Review
In the field of spectrum monitoring,the acquisition of spectrum identity information is mainly implemented by passively detecting and demodulating the emitted signal of STs, which, however, would be hardly completed when the spectrum monitor (SM) is far away from the monitored ST.To tackle such difficulty,[4]designed one novel jamming-assisted monitoring scheme,in which the full-duplex-enabled monitor aims to jam the suspicious destination(SD)deliberately and then moderate the communication rate of the ST,so as to facilitate its clearer monitoring.Subsequently, [5]applied such idea to the surveillance in parallel fading channels, in which the suspicious pair opportunistically selects single channel to communicate over, and the monitor jams in certain number of channels so as to drive the suspicious communication out of the them with reduced rate,and thus facilitates the monitoring of itself over the remained unjammed(monitored) channels.Inspired by[5, 6] further considered the suspicious communication occurs over all channels and then jointly optimized the jamming channels/power to force the suspicious system allocating more power over the unjammed channels,with this way the perceived suspicious signal power of the monitor over those channels could improve accordingly.In addition, [7–9] envisaged the multi-antenna surveillance network and all intended to design the jamming beamformers to enhance the monitoring success probability or the average monitoring rate.[10]studied the two-hop suspicious system and designed an “monitor then jam” scheme to improve the average monitoring rate.[11]considered one surveillance scene of existing two suspicious transceivers and investigated the design of jamming covariance matrix to achieve the monitoring balance.Recently,[12]further designed an alternate-jamming-aided surveillance protocol using two cooperative monitors in the single-hop network,and concurrently developed the performance analysis in term of monitoring non-outage probability and the symbol error probability.Compared to[4–12],[13, 14] studied the more challenge suspicious UAV multicasting or relaying system, in which the suspicious UAV, given certain jamming environment, can adaptively adjust its deployment in favor of maximizing suspicious communication rate and thus will confuse the monitor about its exact jamming effect.[15]proposed another novel monitoring scheme,where the monitor disguises itself as a spoofing relay, and according to different channel conditions, it can adaptively emit the constructive signal or destructive signal to improve or deteriorate the receiving quality of the suspicious signal, respectively.[16–19] further exploited this idea to the surveillance in one-way relaying,two-way relaying,multi-relay or multiple-link suspicious communication system,where the monitor can act as an assister,a jammer or a monitor.
1.3 Motivations
Although fruitful achievements have been created in the field of wireless surveillance,there still exist some key problems to be solved.First, the performance evaluation indicators are relatively scarce.To be specific, except for our previous work [20], no any literatures tried to discuss another important indicator,i.e., the ergodic monitoring rate, which usually appears to characterize the system performance in the delay-tolerant transmission mode.Second, most previous works assumed the monitor operates in fullduplex mode and even thought the self-interference signals can be eliminated completely.However, the consideration of half-duplex monitor is more practical and deserves high attention.Third, with the prosperous development of Internet of Things industry, the suspicious nodes (generally are energy-constrained)can also evolve into low-power sensors to deploy in specific areas, such as the military base, to silently sense the environment and upload the collected data to their center.Under such background, initial works[21, 22] considered the surveillance in suspicious wireless powered communications (WPC).However,both[21]and[22]only studied the special case of existing one suspicious pair and also gave no concerns to the ergodic monitoring rate issue.Moreover, [21]even assumed the instantaneous gains of the suspicious links can be grasped by the monitor, which is hard to realize practically.
Motivated by above,we propose a jamming-assisted proactive spectrum monitoring with one half-duplex SM to cope with the potential SWPC in DSSN,which owns the effect of “one stone, two birds”.The main contributions of this paper are summarized as follows:
• For the proposed scheme,we first specific the detailed actions of SM, which includes its transmit power in block 0 for assisting STs energy transfer,the set of blocks for jamming and the corresponding jamming power in subsequentNblocks.Note that due to the half-duplex constraint, SM can only monitor the signal of STs in any block without transmitting SMD to the SF.We then derive the general expression of the achievable sum ergodic monitoring rate of the monitor under arbitrary action.
• We formulate the optimization problem,and show that it is highly non-convex and includes numerous continuous/integer variables.However, for the symmetric scene where STs located in a same cluster,we provide one key conclusion with strict proof,i.e.,SM should always assist energy transfer in block 0 with tolerable maximum power.In addition, given the number of blocks (K) for SMD transmitting, SM should also exploit the maximum power to transmit its SMD data and jam the blocks from 1 toK, so as to maximally enhance the energy accumulation of the lastN−KSTs from the jamming signals and concurrently induce the power beacon to allocate more energy to them as much as possible.Armed with this,the following work is only to optimize the value ofK, for which we further reveal one fundamental trade-off: asKincreases, the remained number of blocks(N−K)that the SM can monitor would linearly decrease,which is undesirable.However,the perceived suspicious signal power of SM in each of theseN−Kblocks would enhance undoubtedly.Hence the simple one-dimensional search is necessary to find the optimalK.The whole optimization process only requires the statistical channel state information(CSI)of the suspicious system and thus can be implemented practically.
• We also study the scene where all STs are randomly distributed.In such scene, givenK, we find that the conclusion of jamming in blocks from 1 toKwould no longer hold and cannot guarantee the optimality shown in the symmetric scene.Hence, we further propose one lowcomplexity greedy blocks selection scheme to approach the exhaustive search-based blocks selection scheme.Numerical results show that the proposed jamming-assisted monitoring schemes can achieve pretty good performance compared to conventional passive monitoring and some benchmarks.
1.4 Organization of This Paper
The rest of this paper is organized as follows.The system model is presented in section II.In section III,the detailed optimization problem formulation is provided.In section IV,V and VI,the analysis and optimization of the proposed schemes are developed along with the complexity analysis.In section VII, simulations are conducted to characterize the performance of the proposed schemes.Finally,conclusions are drawn in section VIII.
II.SYSTEM MODEL
As illustrated in Figure 1,there areJ+Nhalf-duplex transmitters who have accessed the available spectrum with dynamic spectrum access strategy and established communication with SD1, the processes of which are under the supervision of one SM.STs are assumed to have no other embedded energy sources,and thus should firstly harvest energy from the radio signals emitted by the power beacon(PB)called wireless power transfer systems.2The PB is equipped withM ≫1 antennas for the purpose of enhancing energy transfer efficiency and each of transmitters is equipped with one antenna due to the hardware limitation.The SM firstly monitors the radio signals emitted by these transmitters via passively spectrum monitoring.When SM initially distinguishesN(N ≥2) suspicious transmittersfrom the legitimate transmitters(LTs), special spectrum monitoring is started to these STs.Specifically,for the suspicious system,similar to[23–25], we assume that the suspicious system operates in TDMA mode.The suspicious system can also adopt the FDMA or rate-splitting multiple access[26],and thoses cases will be discussed in our future work.The communications of each data block take place in transmission blocks of durationT(without loss of generality,we setT= 1 here),with each block being either an energy harvesting block (denote as block 0)ori-th suspicious information transmission block(denote as blocki,i ∈N={1,...,N}),as illustrated at the top of Figure 2.For the spectrum monitoring system,SM is also equipped with one antenna and works in the practice half-duplex mode.Specifically,SM intends to overhear the signal transmitted byas far as possible after initially determining these STs.With this purpose, in general SM has two monitoring schemes to choose after initially determining STs by passively spectrum monitoring:
• Non-jamming passive spectrum monitoring scheme, denoted by NJPSM.In this scheme,SM continues to monitor the suspicious signal ofpassively during the subsequentNsuspicious information transmission blocks.This scheme is a benchmark case, which is easy to understand, and the corresponding illustration is thus omitted here.
• Jamming-assisted proactive spectrum monitoring scheme, denoted by JPSM.In this scheme, generally speaking SM transmits its SMD to SF,and concurrently exploits such signal to transmit the wireless energy toduring block 0.Then in the subsequent blocki(∀i ∈ N), SM can choose to monitor the suspicious signal of STipassively or jam the SD(namely transmit its SMD to SF) instead, but cannot implement these two actions concurrently due to its half-duplex constraint.3As illustrated at the bottom of Figure 2,we provide an example that SM deliberately interferes the transmission of block 1,and then tries to monitor the suspicious signals ofin blocks from 2 toN.Here we want to emphasize that,when SM decides to act as a jammer in blocki,which is not only jam the SD,but also transmits SMD to SF,can perform opportunistic energy harvesting from the jamming signal transmitted by SM (for instance, we can observe from the bottom of Figure 2 that the energy transfer occurs from SM towhen SM jams in block 1).Whenstart the transmission, by exhausting the accumulated energy harvested from the jamming signals in previous possible blocks, their transmit power can be further enhanced.4However,this phenomenon would instead promote the effective spectrum monitoring by SM,as will be clear latter.
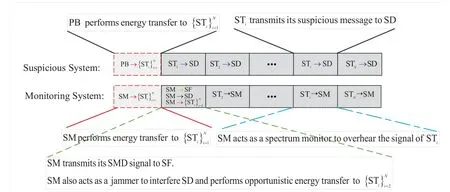
Figure 2. Top: the diagram of the transmission protocol of the suspicious system.bottom: an illustration of the detailed spectrum monitoring strategy in the proposed JPSM,in which SM performs wireless energy transfer to in block 0,transmits its SMD signal to SF and jams the SD(also performs opportunistic energy transfer toin block 1 and monitors the suspicious signals ofin blocks from 2 to N.
We assume that all the channel links are constituted of large-scale path loss with exponentαand statistically independent small-scale Rayleigh fading.In addition,we denote the distance of the links PB→STi,STi →SD,STi →SM(SM→STi)and SM→SD bydPTi,dTiD,dTiM(dMTi,dMTi=dTiM)anddMD,respectively,and the PB→SM link is not considered here due to that it has no effect on the subsequent analysis.The corresponding small-scale channel fading coefficients over blockj(j ∈{0,1,...,N}) are denoted byM ×1 vector hPTi,j, scalarsgTiD,j,fTiM,j(fMTi,j) andεMD,j, respectively.All channel coefficients keep invariant during each data block but vary independently among different frames.The entries of these channel coefficients are complex Gaussian random variables with zero mean and unit variance.
Denote the transmit power of the PB asQP.In addition, we assume that the PB exploits a weighted sum of conjugate energy beamformers for each ST,since it has been shown to be asymptotically optimal for energy transfer [27].Hence, the precoder of the PB over block 0 can be expressed as wP,0=whereθi ∈(0,1),∀i,1 and∥hPTi,0∥denotes the Frobenius norm of a complex vector hPTi,0.Moreover, we consider that SM is a powerful device and further denote the tolerable maximum power of SM for possible jamming to SD in each block asQM,max, where the jamming operation will also opportunistically transfer energy to STs.
In this paper,we consider that the suspicious system works in the delay-tolerant transmission mode and can adaptively adjust the values offor the purpose of maximizing the sum ergodic suspicious communication rate.Since the relevant information of spectrum users has been stored in the spectrum database in advance, SM can obtain part of the relevant information about spectrum users from the spectrum database.Therefore,SM can assess the global statistical CSI of the considered system and thus it aims to maximize the achievable sum ergodic monitoring rate,the definition of which will be given in the follows.
III.PROBLEM FORMULATION
In this section, we aim to first provide the general expressions of the sum ergodic suspicious communication rate achieved by the ST and the sum ergodic monitoring rate achieved by SM in Non-jamming passive spectrum monitoring scheme(NJPSM) and Jamming-assisted proactive spectrum monitoring scheme(JPSM),respectively.Armed with these,we then aim to formally formulate the optimization problem.
3.1 The Sum Ergodic Suspicious Communication Rate and Sum Ergodic Monitoring Rate
3.1.1 Non-jamming passive spectrum monitoring scheme
Let us first focus on the suspicious system.Assuming that the PB in block 0 emits the energy signalswiththen the signalyireceived at the STiis expressed as
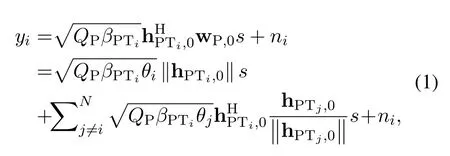

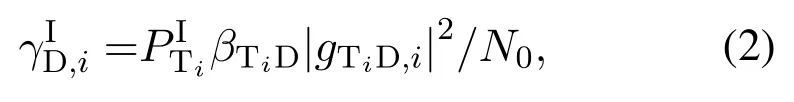
whereβTiD=andN0is the noise power.Then, the ergodic suspicious communication rate of the STi,which is varied with respect to(w.r.t.)θi,can be derived as
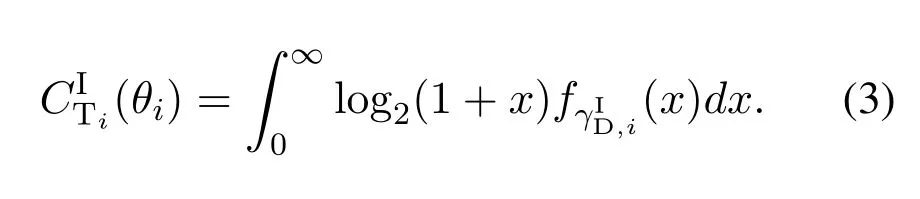

We now focus on the spectrum monitoring system.In NJPSM,SM aims to overheard the suspicious signal of the STipassively for anyi ∈N.The received SNR of SM in blocki ∈Ncan be expressed as

whereβTiM=In this paper, we adopt the same assumption made in[9–22],i.e.,ST is not aware of the true identity of SM and just regards it as the normal user sharing the same spectrum,hence no dedicated coding as in conventional physical-layer security is applied to prevent the monitoring by SM.Therefore,as defined in thoes works,only whenβTiM|fTiM,i|2≥βTiD|gTiD,i|2, can SM decode the corresponding suspicious signal with arbitrary small error probability and then the monitoring rate is equal to the suspicious communication rate log2(1+,otherwise it is impossible for SM to decode the suspicious information without any error and then the monitoring rate is equal to zero.Note that when the spectrum monitoring link is worse than the suspicious link, SM may still obtain useful information from its received signal.However,same with[13]and[18], we in this paper consider a more stringent requirement that the message from the STs needs to decoded with arbitrarily small error probability at the ST to achieve the spectrum monitoring goal.Armed with above definition, we can derive the ergodic monitoring rate achieved by SM for the suspicious signal of the STias
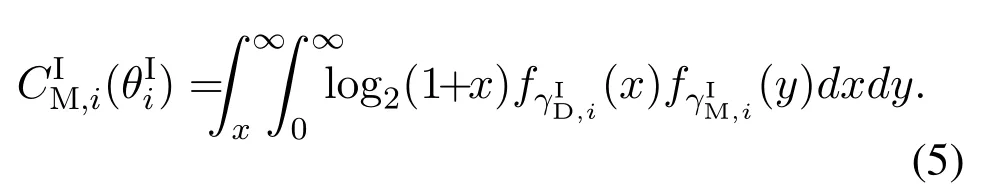
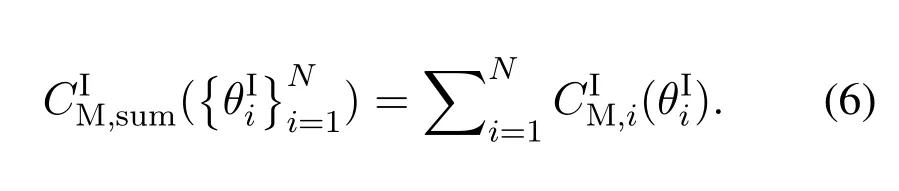
3.1.2 Jamming-assisted proactive spectrum monitoring scheme
As explained in section II, in this scheme, SM can perform flexible energy transfer, jamming or monitoring in each block.To be specific, we now denote the transmit power of SM in block 0 asQM,0,QM,0≤QM,max.In the subsequentNblocks,we also denote the set of blocks that SM decides to jam and overheard as ΩJamand ΩMon, respectively.In addition, ΩJam(j)denotes thej-th element in ΩJam.Due to the half-duplex constraint,we have ΩJam∩ΩMon=∅and ΩJam∪ΩMon=N.NJPSM in fact corresponds to the case thatQM,0= 0, ΩJam=∅andΩMon=N.In JPSM, for block ΩJam(j), we further denote the corresponding jamming power of SM asQM,ΩJam(j),QM,ΩJam(j)≤QM,max.For simplicity, we denote the set of SM’s actions as AM=
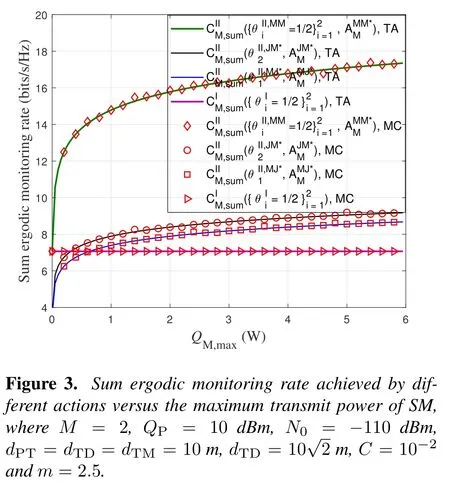
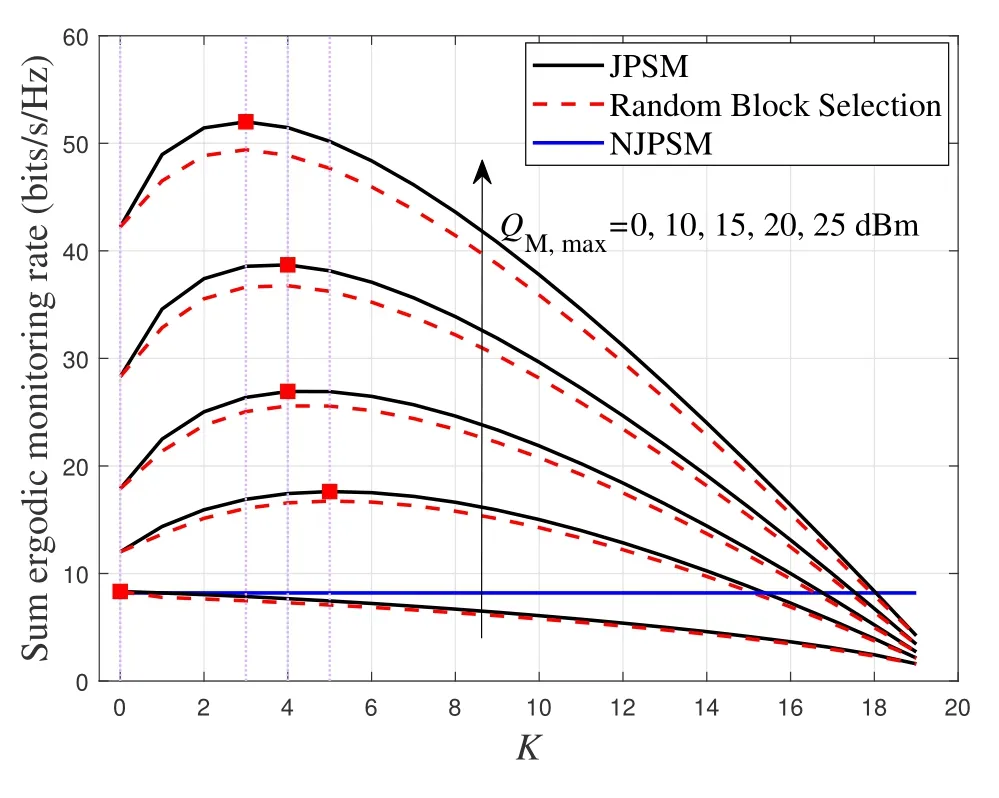
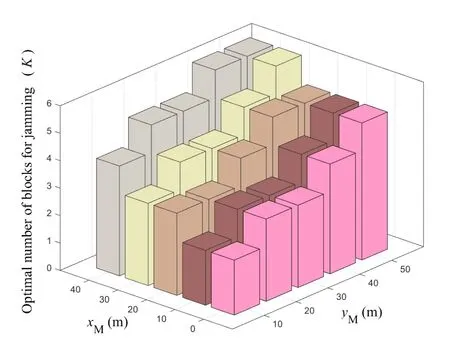
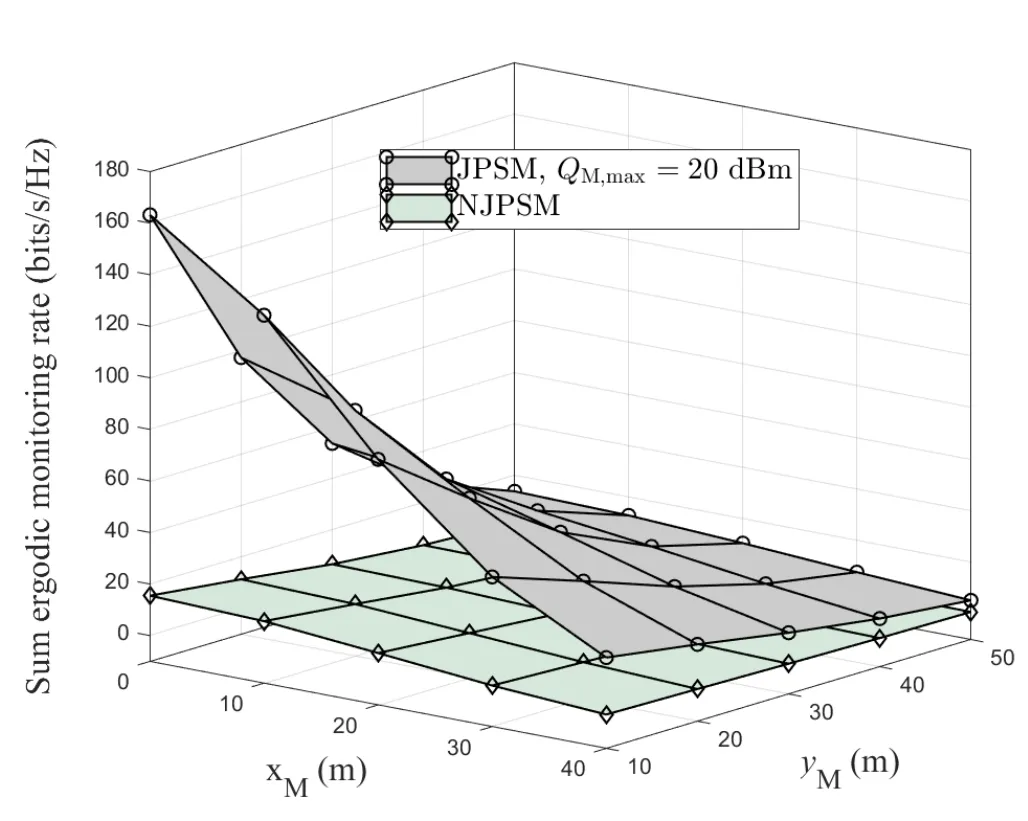
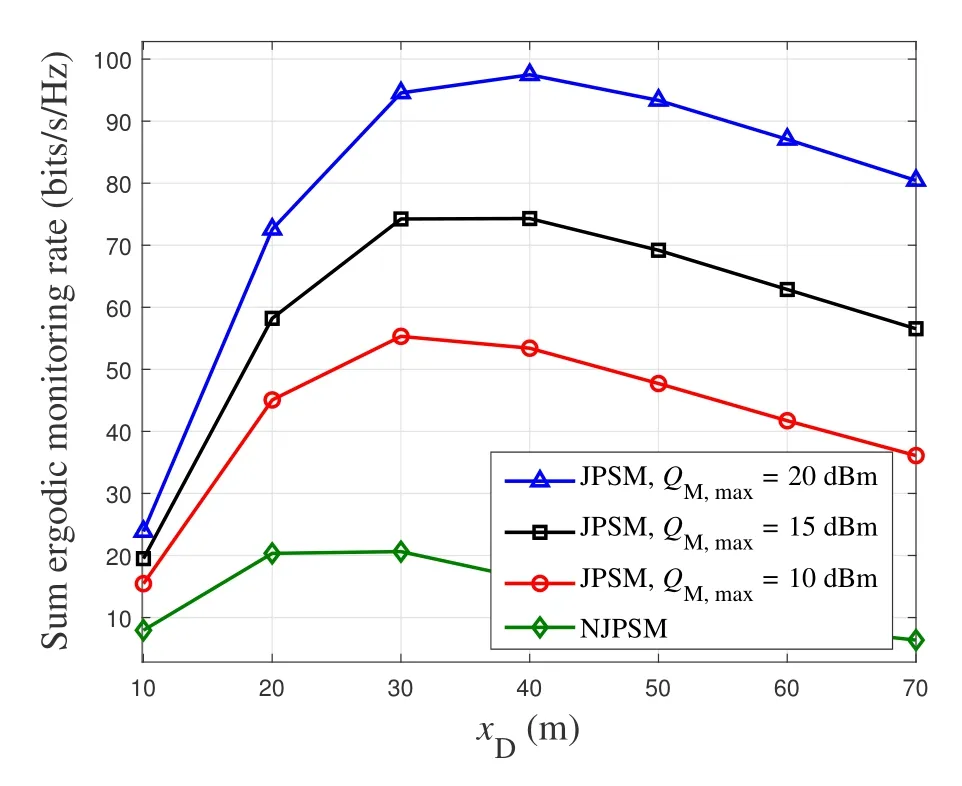
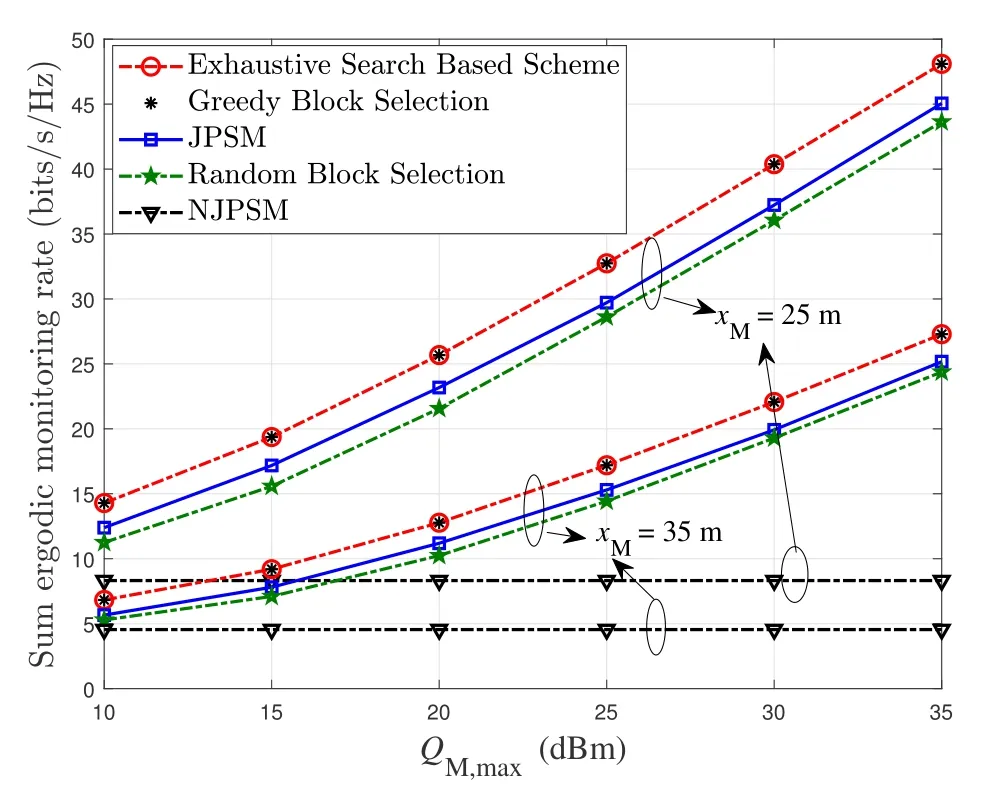
For each suspicious transmitter STi, it can harvest additional wireless energy from SM in block 0.In addition, before starting to transmit its suspicious information,the STican also perform opportunistic energy harvesting from the jamming signals transmitted by SM in any block ΩJam(j),but ΩJam(j)should satisfy that 1≤ΩJam(j) The transmit power of the STiin blockithus isand the corresponding received SNR(signal to interference plus noise ratio, SINR) at the SD can be expressed as whereβMD=Then, the ergodic suspicious communication rate of the STican be derived as For SM, it can only perform passive monitoring in blocks that belongs to ΩMon, and its received SNR in blocki,i ∈ΩMon,can be expressed as According to the(6)and(11), we now can formulate the optimization problem in term of maximizing the sum ergodic monitoring rate of SM as The problem in (12) is highly non-convex due to that SM not only requires to decide which blocks to jam (opportunistic energy transfer) or monitor, but also needs to optimize the corresponding transmit power.More importantly, given each AM, the values ofcan be adaptively optimized by the suspicious system via above analysis, which will in turn affect the spectrum monitoring performance of SM.Hence,for the purpose of easy understanding,in next section,we first consider the case of existing two STs,e.g.,ST1and ST2,we then provide insightful conclusions in such case,so as to pave the way for the analysis of the general case,i.e.,N >2,in section V. In this section,we first assume the symmetrical scene,i.e.,dPT1=dPT2=dPT,dT1D=dT2D=dTDanddMT1=dMT2=dMT.Note that such assumption can be practical in the case that all STs(for example,sensors)are close to each other and coexist in the same cluster, hence the distance between each of them and the PB, SD or SM can be approximately same.The asymmetric scene will be discussed in section VI. For the purpose of comparison,we now also derive the sum ergodic suspicious communication(spectrum monitoring)rate in NJPSM as Proof.This Proposition 1 is established due to the following two aspects: • First,from(7),QM,0can be regarded as an additional transmit power increment of the PB,when the value ofQM,0is set asQM,max, we can see that: i) the additional harvested energy of both ST1and ST2in block 0 will achieve the maximum and keep same.Such sameness thus will not change the energy allocation of the PB. Hence, whenQM,0=QM,1=QM,max, according to i),iii)and iv),the harvested energy by the ST2from both the PB and SM will achieve its maximum, then its transmit power (so does the perceived suspicious signal power of SM) in block 2 will be greatly enhanced.Hence, according to the definition shown in(5)or(11),the corresponding ergodic monitoring rate of the SM,which is monotonically increasing w.r.t.the transmit power of the ST2,can achieve its maximum.This completes the proof. We in the above provide the simple physical explanation.For the strict derivation,please see the theoretical analysis in section V and the part A.2 of Appendix A,for the comprehensive details. Proposition 2 implies that, for SM, even the number of block(s) for jamming and the jamming power are fixed,the selection about jamming which block(s)can still affect the monitoring performance.In next section, we will generalize this finding in theN >2 case. Proof.In JPSM,whenQM,max→0,both the amount of the harvested energy of the ST1(ST2)from SM in block 0 or the jamming effect of SM in block 1 (2)are very little and can be neglected.However, compared to the cases that SM in NJPSM and JPSM(under the actionalways monitors in blocks 1 and 2, SM in JPSM (under the actionsandcan only monitor in one block.Hence we can obtain the first conclusion.In addition, in JPSM, whenQM,max→∞,due to that the amount of the harvested energy by the ST1(ST2) in block 0 already goes to infinity, so does their transmit power (the perceived power of SM) in block 1 (2).Hence, it is more advisable for SM to overhear in subsequent two blocks.Moreover, in NJPSM, evenQM,maxis very large, the ST1(ST2)cannot harvest any additional energy from SM.In light of these two aspects, we can obtain the second conclusion.This completes the proof. To be more intuitive, the conclusions of Propositions 1, 2 and 3 are illustrated in Figure 3.The comparision between the theoretical analysis and Monte Carlo simulation of the proposed Propositions 1, 2 and 3 is also given in Figure 3,which shows that the Monte Carlo simulation results are almost consistent with the theoretical analysis results,which can further prove the correctness of our closed-formed analysis.In addition to these,we can further observe that,under the case of two STs, the actionof JPSM takes over the absolute advantage compared to,this is mainly due to that under, only one suspicious transmitter (ST2) can perform additional energy harvesting from the jamming signal in block 1.Considering the little energy accumulation effect underSM would rather choose to monitor in more blocks.However, in the general case (N > 2), due to the stronger energy accumulation effect, we will see that the optimal number of blocks for jamming generally should be larger than zero,as shown in section VII. In this section, we consider the general scene with N > 2 STs, and then aim to further determine and analyze the optimal design for JPSM. To start with, we first want to figure out one key problem, i.e., when the number of blocks K ≥ 0 for jamming are fixed,SM should select which power to jam which K blocks? We answer this question in Proposition 4. Proposition 4.In JPSM, given |ΩJam| = K,the optimal action of SM should be(K) ={QM,0= QM,max,ΩJam= {1,...,K},ΩMon={K+1,...,N},=1 =QM,max} Proof.Please see Appendix A. Armed with Proposition 4,we now can simplify the problem in(12)as follows: Here K should be smaller than N, otherwise SM can overhear nothing.In addition,we can expect that,for SM, as K increases, due to its half-duplex constraint,the number of blocks remained for monitoring,i.e.,N−K,would linearly decrease,which is undesirable.However, due to the stronger energy accumulation effect,each of the last N−K STs can opportunistically harvest more energy from the jamming signals in the first K blocks and then the perceived suspicious signal power of SM in each of the last N−K blocks would enhance.Hence,there may exist an interesting trade-off in deciding the optimal K, which is another key finding of the studied problem. To proceed,given the action(K),based on(7),we can first expressas Based on(8),(9),(22)and by further exploiting the property that E[log2(1+x)]≥log2(1+eE[lnx]),we can derive the tight lower bounds of(θi,(K)),i ∈{1,...,K}as whereNQβ1= (QPβPT+QM,maxβTMi)βTDEQ,EQ=eψ(1)+eQβNEi(−QβN),NQβ2= (QPβPT+QM,maxβTM(K+1))βTDeψ(1). Since the additional harvested energy by each of the lastN −KSTs is totally same, hence we can easily see thatLi,∀i ∈{K+1,...,N}is a constant. According to (11), (26) and after some manipulation, we can further derive the lower bound ofas Special Case:WhenM= 1, i.e., when the PB is equipped with single antenna, since no any energy allocation coefficients are involved, hencecan be simplified as Proposition 5.When M= 1, according to(28), we can further derive the closed-form sub-optimal K asin(29), where Ktep=K∗∈Z,W(·)is the Lambert function [29] and ⎿x」represents the largest integer smaller than x. Proof.Please see Appendix B. Under the asymmetric scene,all STs may be randomly distributed and thus the distance between each of them and the PB (the SD or SM) may be different.Nevertheless, under such case, armed with the above analysis in section V, we can still verify that: when SM decides to jam in arbitrary 0≤K ≤N −1 blocks,it should also jam with the maximum powerQM,max.As proved in part A.2 of Appendix A,the key idea to understand such conclusion is that the total harvested energy by each of the STs corresponding to the remainedN −Kblocks must monotonically increase w.r.t.the transmit power of SM, regardless of the adaptive adjustment of the energy allocation coefficients by the PB.Hence, the perceived suspicious signal power of SM in the remainedN −Kblocks would enhance correspondingly and so does its obtained sum ergodic monitoring rate. Therefore, under the asymmetric scene, givenK,to tackle the problem about selecting whichKblocks to jam, generally we can exploit the two-layer search method to find the optimal solution of JPSM.In particular,layer 1 aims to list all possible number of blocks 0≤K ≤N −1 for jamming; given each case of layer 1,layer 2 aims to determine that whichKblocks should be jammed by SM optimally.The exhaustive search method owns a complexity ofO(2N −1).In the sequence, a sub-optimal greedy block selection scheme is further presented to approach of the optimal solution,which only owns a complexity ofO(N),and thus is easier to handle. In this section, we aim to provide numerical results to evaluate and validate the proposed spectrum monitoring schemes.Unless otherwise stated, we set thenumber of antennas equipped at the PB as M = 20,the number of STs as N = 20, the transmit power of the PB as QP=5 dBm,the maximum transmit power of SM is QM,max= 20 dBm, the path-loss exponent as α = 2.5, the channel power gain at the reference distance 1 m as C = 10−2and the noise power as N0=−110 dBm. Table 1.Comparison: The achievable sum ergodic monitoring rate of SM with two actions and under the asymmetric scene. Table 1.Comparison: The achievable sum ergodic monitoring rate of SM with two actions and under the asymmetric scene. QM,max =0 W QM,max =1 W QM,max =2 W QM,max =3 W QM,max =4 W QM,max =5 W AJM∗M 3.68 bits/s/Hz 8.86 bits/s/Hz 9.43 bits/s/Hz 9.76 bits/s/Hz 9.98 bits/s/Hz 10.18 bits/s/Hz AMJ∗M 3.68 bits/s/Hz 15.33 bits/s/Hz 16.18 bits/s/Hz 16.68 bits/s/Hz 17.03 bit/s/Hz 17.31 bits/s/Hz Algorithm 1.The greed block delection scheme.1: Input: Ω(0)Jam =∅,Ω(0)Mon ={1,...,N}.2: Optimization:3: For k =1:N 4: Set Ω(k)Jam =Ω(k−1)Jam ∪k and Ω(k)Mon =Ω(k−1)Mon /k.5: Compute the values of CIIM,sum({θIIi}i∈Ω(k−1)Mon ,A(k−1)M ) and CIIM,sum({θIIi}i∈Ω(k)Mon,A(k)M ) by means of the similar methods for deriving(26)and(27).6: If CIIM,sum({θIIi}i∈Ω(k)Mon,A(k)M ) ≥CIIM,sum({θIIi}i∈Ω(k−1)Mon ,A(k−1)M ), then updateΩ(k)Jam and Ω(k)Mon; otherwise mark Ω(k)Jam = Ω(k−1)Jam and Ω(k)Mon =Ω(k−1)Mon .7: End for 8: Output: Ω(N)Jam and Ω(N)Mon. Let us first focus on the symmetric scene.In order to verify the validity of the proposed JPSM, we now also consider another benchmark scheme as “random block selection”, in which SM in block 0 assists energy transfer toand given 0 ≤K ≤N −1,SM implements jamming in random K blocks belonging to{1,...,N}and monitoring in the remained N −K blocks.The transmit power of SM in block 0 and the random K blocks is QM,max.The sum ergodic monitoring rate of such scheme is computed by averaging 103simulations. We assume that all nodes are located in a 2-D topology, where the PB, the STs,9the SD and SM are located at(−10,0)m,(0,0)m,(25,0)m and(xM,yM)m, and the values of xMand yMcan be varied here in order to observe the effect of the channel quality of the monitoring/jamming/opportunistic energy transfer on the obtained sum ergodic monitoring rate. Figure 4 presents the sum ergodic monitoring rate of the monitor w.r.t.K and QM,maxin different schemes,from which we can observe that: i) the performance achieved by NJPSM is always inferior to JPSM,since the former obvious is a special case (AM={QM,0=0,ΩJam=∅,ΩMon=N}) of the latter; ii)in JPSM,given different power budget QM,max, there always exist one optimal K (e.g.K∗= 5 when QM,max= 10 dBm.K∗= 4 when QM,max= 15 dBm) to maximize the objective, which verifies the fundamental trade-off revealed in section V;iii)when the power budget QM,maxincreases, the value of K∗would first increase and then decrease.Especially,when QM,maxis small, e.g.−10 dBm, the SM can only give rise to very little effects of jamming to the SD and opportunistic energy transfer to the STs,hence in such case it is more preferable for the SM to only assist energy transfer in block 0 and then overhear in subsequentNsuspicious information transmission blocks,i.e.,K∗= 0.Moreover,whenQM,max→∞,predictably the SM will also perform energy transfer in block 0 and then always monitor.This phenomenon is perfectly consistent with Proposition 3 and hence the reason is not provided here again; iv) compared JPSM with random block selection scheme, since the latter cannot maximize the energy accumulation effect to the STs as in the former, hence for eachK(except forK= 0), the perceived sum suspicious signal power at the ST in the latter would be absolutely smaller than that of in the former, then we can see JPSM always performs better than the random block selection scheme.This phenomenon also verifies the necessity of optimizing the set of blocks for jamming. Figure 4.Sum ergodic monitoring rate of different schemes versus the number of blocks for jamming (K) with different maximum power of the monitor(QM,max),(xM,yM)=(0,35)m. Figure 5 and 6 then focus on the impact of ST’s location on the monitoring performance.Specifically,Figure 5 illustrates the optimal number of blocks for jammingK∗w.r.t.different coordinates of the ST,from which there are two points should be noticed:i) givenxM, asyMincreases (this corresponds to the case that SM is far away from ST), all of SM’s jamming/opportunistic energy transfer/monitoring abilities will show a rapid downward trend.Instead of listening in more blocks with little suspicious signal power perceived in each of these blocks, it is more advisable for SM to properly jam in more blocks, so as to opportunistically enhance the transmit power of STs corresponding to the unjammed blocks as far as possible, hence we can see that the value ofK∗will monotonically increase asyMincreases; ii)givenyM,asxMincreases(this corresponds to the case that SM is move from STs to SD), obviously the jamming effect to the SD will enhance, but such effect actually can only force the power beacon to transmit more limited energy to the STs corresponding to the unjammed blocks, and thus actually has smaller impact on the spectrum monitoring performance compared to the opportunistic energy transfer effect to ST, which combines with the quality of the monitoring links will decay rapidly asxMincreases.Hence, due to the same reason mentioned in i),the value ofK∗will also monotonically increase asxMincreases. Figure 5. Optimal number of blocks for jamming (derived in (29)) of JPSM versus different location of the SM,QM,max =20 dBm,M =1. Figure 6. Optimized sum ergodic monitoring rate of NJPSM and JPSM versus different location of the monitor,M =1. Accordingly,Figure 6 shows the optimized sum ergodic monitoring rate achieved by NJPSM and JPSM w.r.t.the ST’s location.Due to the reasons mentioned earlier, obviously we can see that the spectrum monitoring performance of both schemes will deteriorate gradually asxMoryMincreases. Figure 7 further presents the impact of SD’s location on the spectrum monitoring performance, wherexDdenotes the horizontal coordinate of SD.We can find that: asxDincreases,on the one hand,the quality of the suspicious communication links becomes worse and would be poorer than that of the monitoring links with larger probability;on the other hand,the ergodic suspicious communication rate would decrease.These two aspects imply that,asxMincreases,SM can only overhear a smaller amount of suspicious information,but the spectrum monitoring quality would improve gradually, hence due to such trade-off, we will see that the sum monitoring rate would first increase and then decrease.Predictably,whenxD→∞,since the ergodic suspicious communication rate would tend to zero,hence the corresponding ergodic monitoring rate would also approach zero undoubtedly. Figure 7. Optimized sum ergodic monitoring rate of NJPSM and JPSM versus different locations of SD,(xM,yM)=(0,20)m. We now focus on the asymmetric scene.Specifically,we consider that there areN= 10 STs,the locations of which are randomly distributed in a rectangle with the coordinates of the four vertices being (−5,−15)m,(−5,15)m,(5,−15)m and(5,15)m,respectively.Under such setup, we aim to compare the achievable sum ergodic monitoring rate of different schemes,which is the average value of the 103simulations corresponding to the randomized coordinates of STs.As shown in Figure 8,the achievable performance of the proposed greedy block selection scheme almost approaches that of the exhaustive search based scheme,but the former owns very low complexity and thus can be implemented in practice.In addition, under the asymmetric scene, JPSM would no longer be valid,this is mainly due to that, STs corresponding to the smaller(larger)block index number may be closer to(far away from)SM,hence if SM still jams firstly and overheard subsequently,it will waste the fine chance to overhear the signals of the near ST,bring little opportunistic energy transfer effect to the remote STs and concurrently perceive poor suspicious signal power from such STs.Also, the random block selection scheme actually has paid no attention to the difference of STs’coordinates and thus will achieve the inferior performance at the same time.In addition, same to the symmetric scene,NJPSM has not exploited the advantage of the opportunistic energy transfer effect and thus achieves the worst performance. Figure 8. Sum ergodic monitoring rate of different schemes versus the maximum transmit power of SM under the asymmetric scene. In this paper, we design and analyze the jammingassisted spectrum monitoring scheme with one halfduplex SM for the suspicious WPCN in DSSN,which can extract spectrum identity information of STs timely and accurately to ensure the spectrum security of dynamic spectrum sharing.For the proposed scheme, we first specify the detailed actions of SM and accordingly derive the general expression of its obtained sum ergodic monitoring rate.We then formulate the optimization problem and show that it is highly non-convex.However, under the symmetric scene,after strict proof and analysis, we can equivalently transform the optimization problem into the extremely simple problem involving only single integer variable and further reveal a fundamental trade-off.Under the asymmetric scene, we find the certain part of the conclusions in the symmetric scene would no longer hold and hence correspondingly we further propose one greedy blocks selection scheme to approach the exhaustive search based scheme.Simulation results show that the proposed scheme can obtain higher spectrum monitoring performance than the passive spectrum monitoring and some benchmarks.Namely, the proposed scheme can obtain more accurate and effective spectrum identity information,which can provide basic support for fine-grained spectrum management and a solution for spectrum security in DSSN. ACKNOWLEDGEMENT This work is supported by the Natural Science Foundations of China (No.62171464, 61771487) and the Defense Science Foundation of China (No.2019-JCJQ-JJ-221). NOTES 1The dynamic spectrum sharing strategy is not discussed in our model due to that our aim is to confirm the spectrum identity of STs after dynamically accessing the available spectrum without considering a specific dynamic spectrum access strategy. 2These systems can be classified to simultaneous wireless information and power transfer(SWIPT)systems and WPC systems.In SWIPT system,the radio signal is used to transfer both information and power at the same time,whereas in WPC systems,the STs harvest energy from a radio signal over a downlink channel to facilitate its communication with its SD.Compared with SWIPT,WPC is more likely to be used in engineering due to the practical hardware limitations of these STs.Therefore,we establish a system model for WPC in this paper. 3The performance of SMD transmission is not discussed in our model,which is only one of supplements to the SMD transmission. 4Similar to[31],the harvested energy of each ST from the radio signal emitted by the previous scheduled ST is ignored in this paper,as such kind of energy suffers from twice channel fading and is very little. 5Since we mainly consider the design of the monitoring strategy from the viewpoint of SM,hence here we just setφ=1 for simplification.Note that such value has no any impact on the conclusions obtained in this paper. 6Note that SM cannot always jam in blocks 1 and 2,otherwise it cannot implement spectrum monitoring anymore.Hence such action is not listed here. 8Note that such setting is reasonable by considering a 2-D topology and further assuming that the PB,the ST1,the ST2,the SD and SM are located at(−10,0)m,(0,0)m,(0,−5)m,(10,0)m and(0,5)m. 9In the symmetric scene,to provide the insightful conclusions and facilitate analysis,the STs in one cluster are assumed to be located at the same point.In the asymmetric scene,we will assume that each of the STs is randomly distributed. APPENDIX A:PROOF OF PROPOSITION 4 A.1 The Optimality of Jamming in the Given Blocks The conclusion of Proposition 4 can be proved using proof by contradiction.Specifically,givenK,we now denote two actions as A.2 The Optimality of Assisting Energy Transfer and Jamming Using the Maximum Power Without loss of generality, givenK, we denote two actions as where ∆x ≥0. APPENDIX B:PROOF OF PROPOSITION 5 The first-order derivative ofw.r.t.Kis expressed as By making the first-order derivative equal to zero,we have
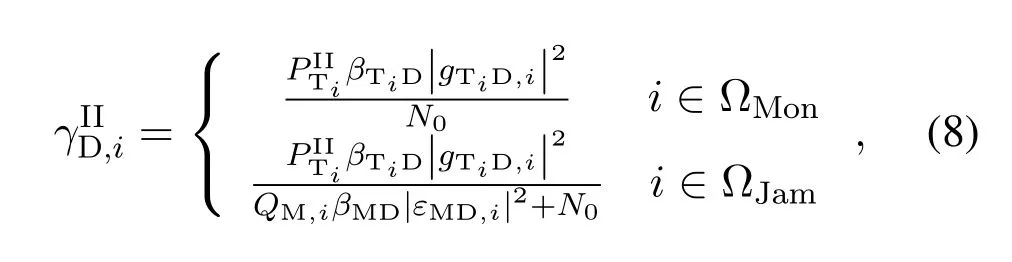
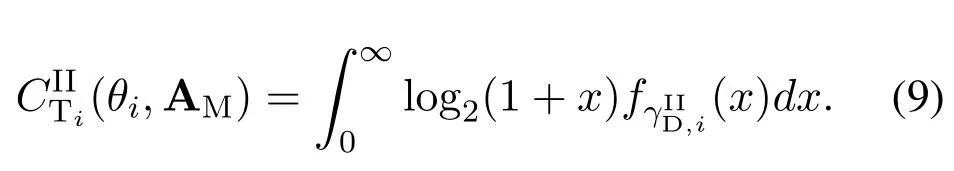
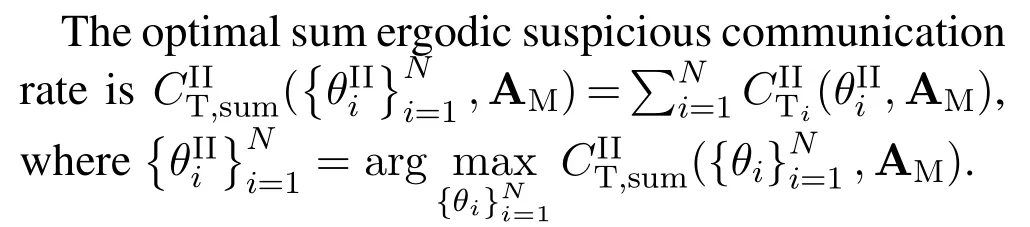
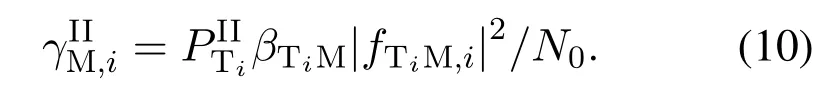
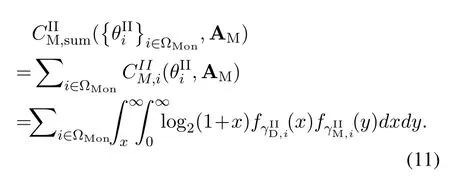
3.2 Optimal Problem Formulation
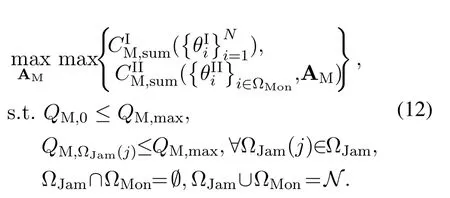

IV.OPTIMAL DESIGN FOR JPSM UNDER THE CASE OF TWO STS


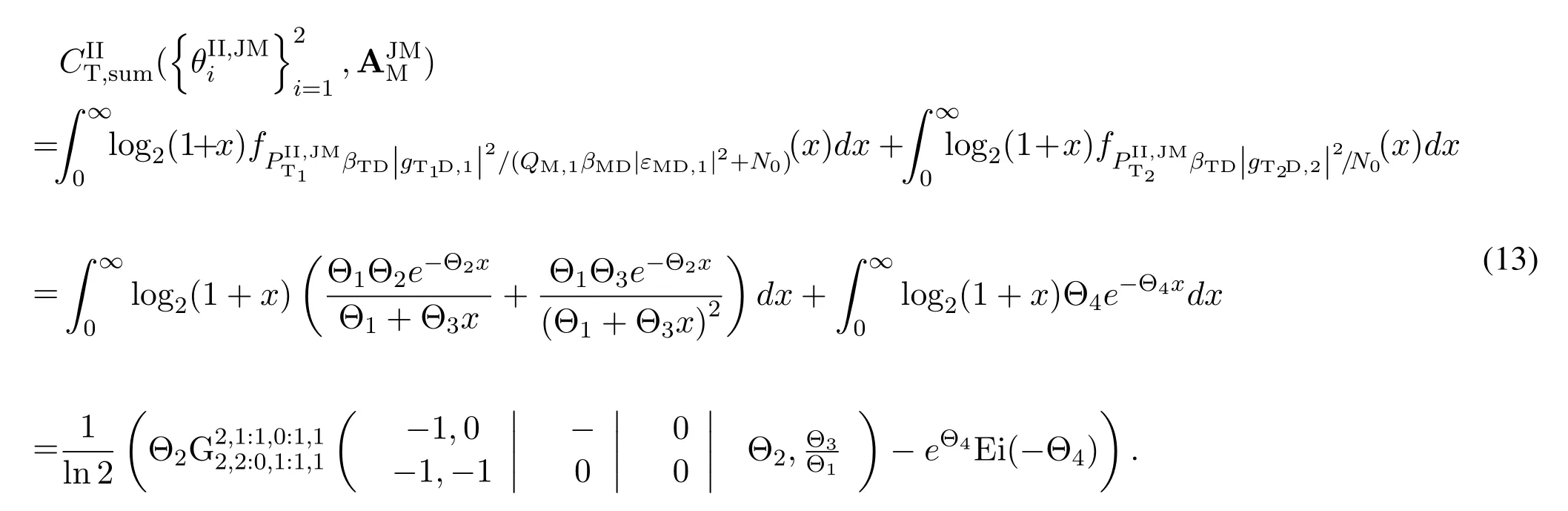


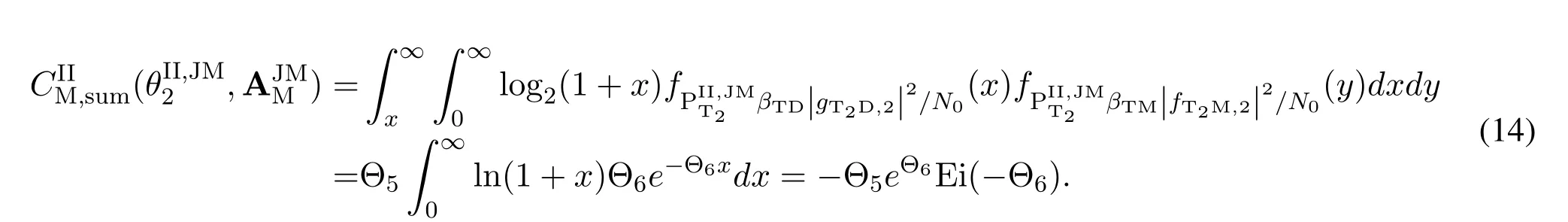

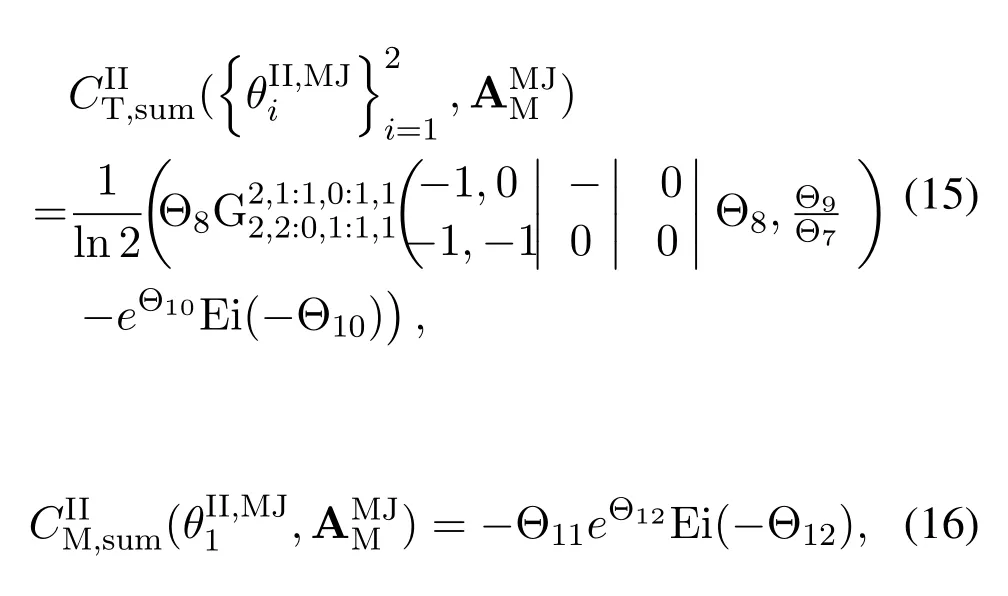

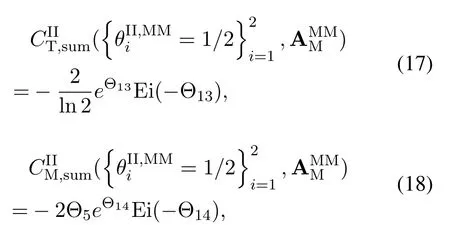
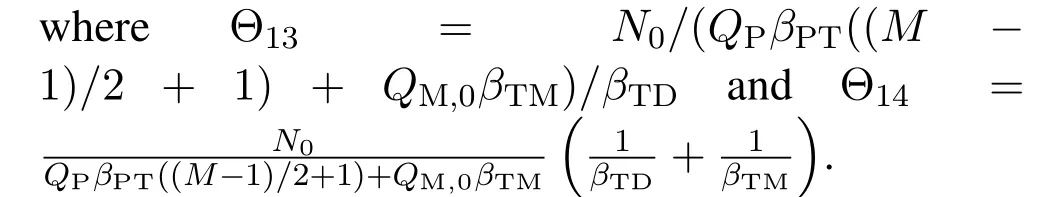
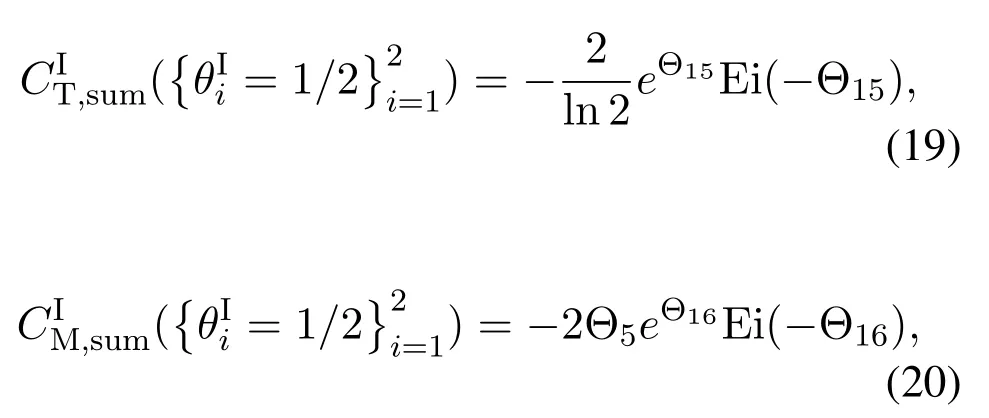





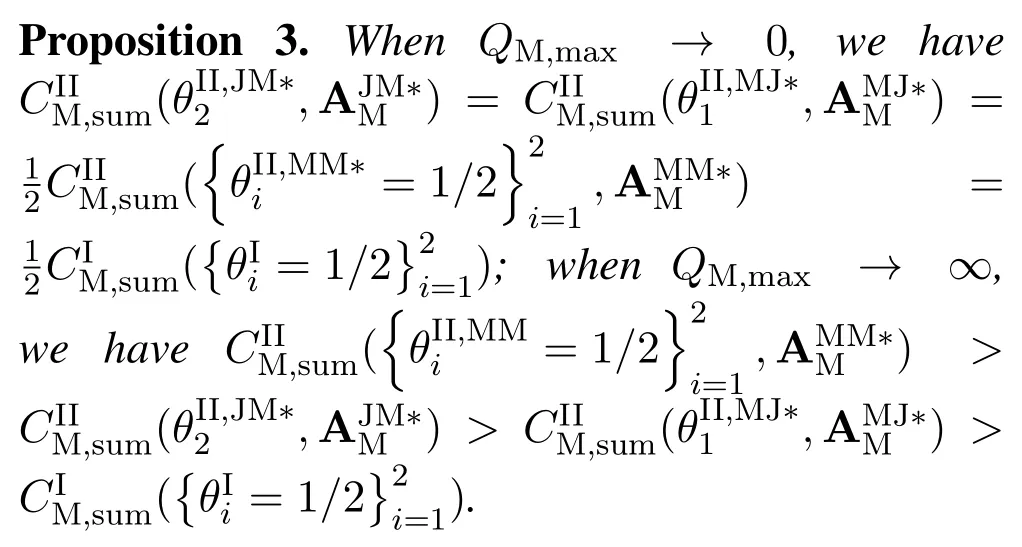
V.OPTIMAL DESIGN FOR JPSM UNDER THE CASE OF ARBITRARY NUMBER OF STS



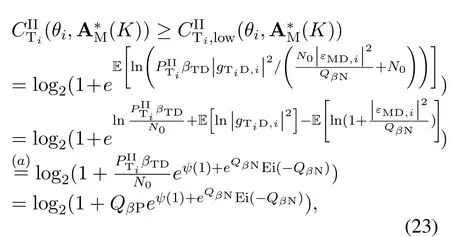

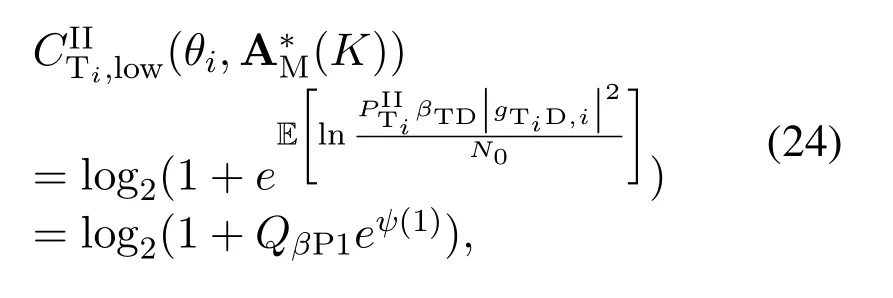




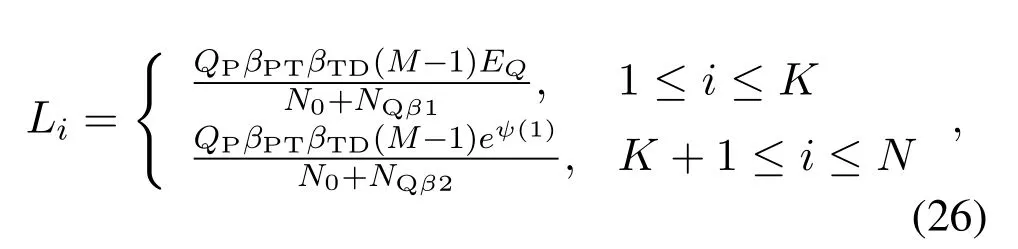
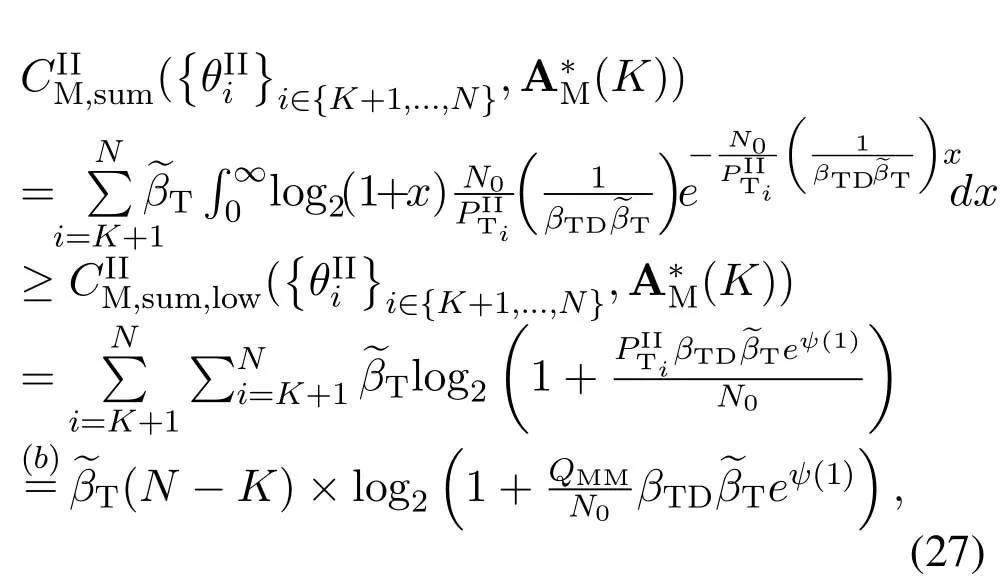

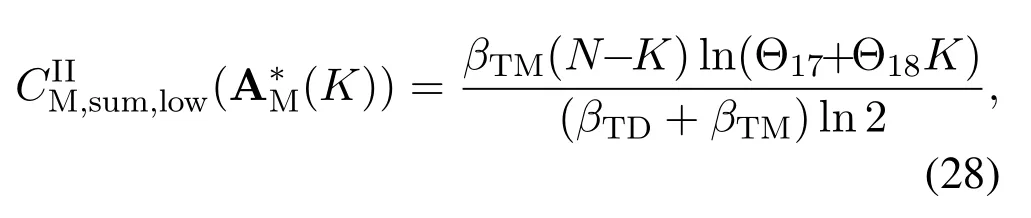
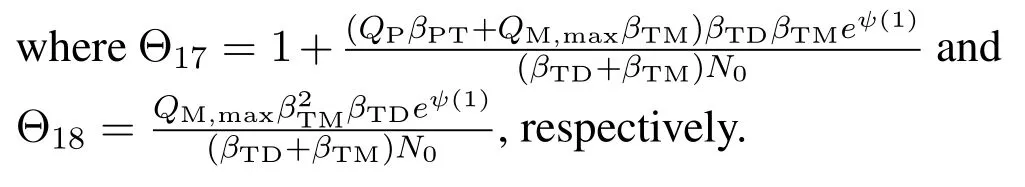
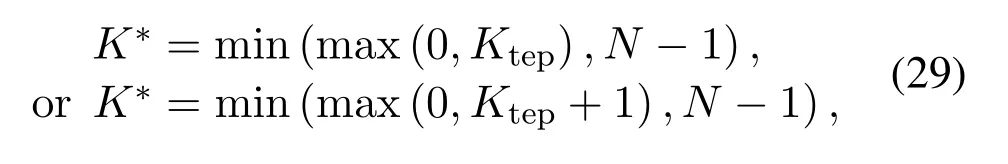
VI.OPTIMAL DESIGN FOR JPSM UNDER THE ASYMMETRIC SCENE



VII.SIMULATION RESULTS


7.1 Symmetric Scene
7.2 Asymmetric Scene
VIII.CONCLUSION

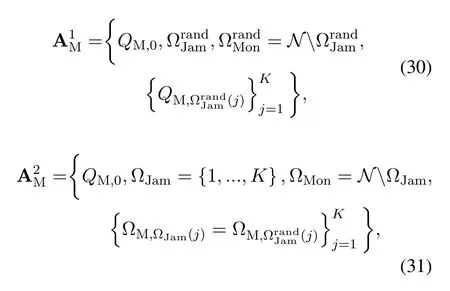
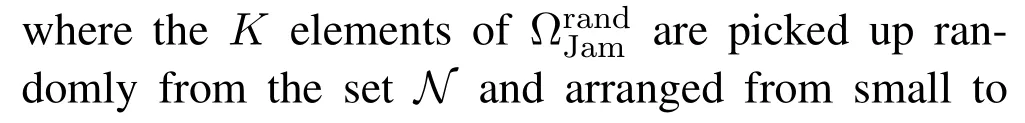

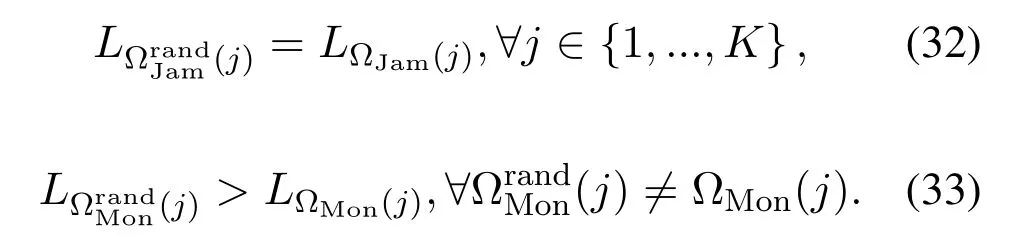

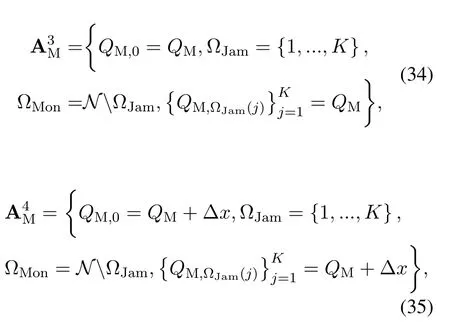

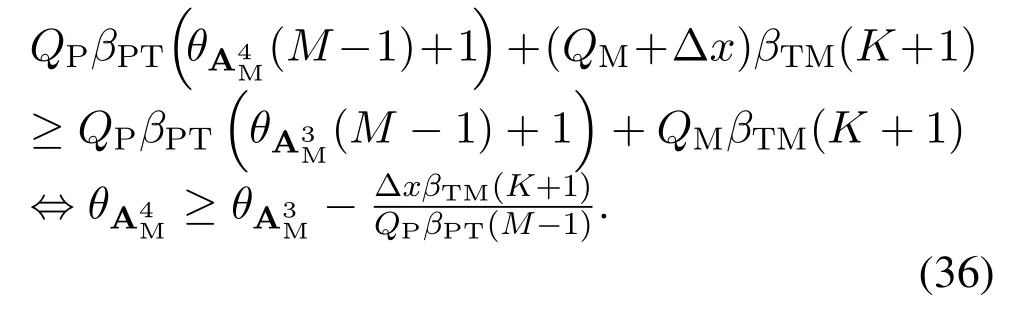
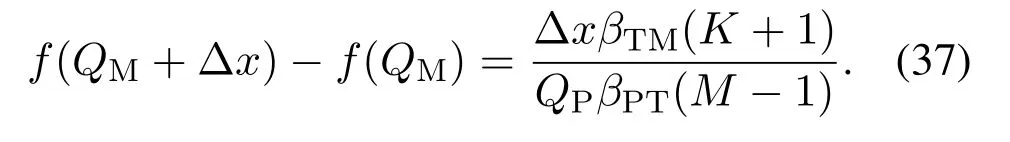

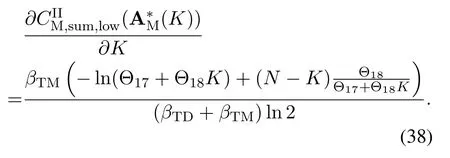
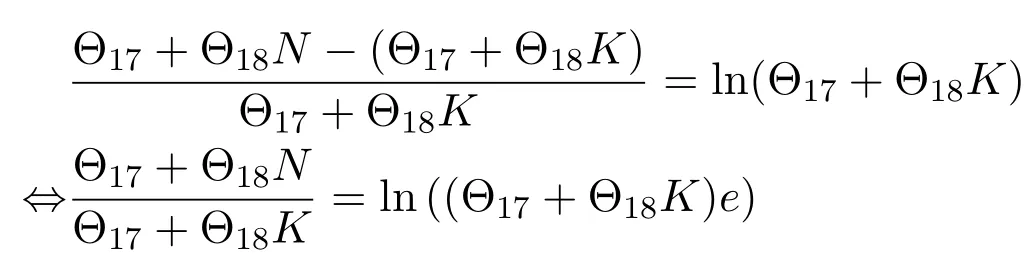
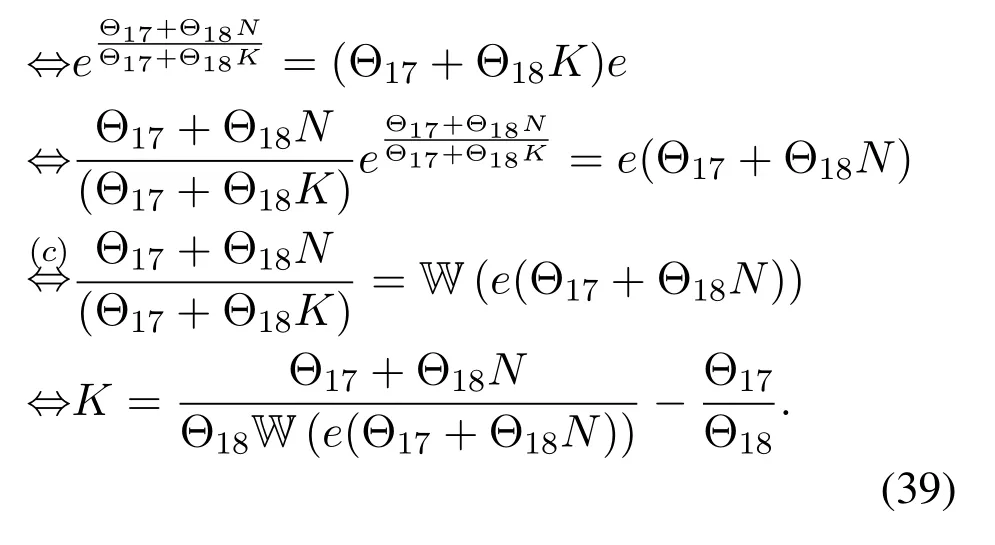
- China Communications的其它文章
- An Overview of Wireless Communication Technology Using Deep Learning
- Relay-Assisted Secure Short-Packet Transmission in Cognitive IoT with Spectrum Sensing
- Frequency-Hopping Frequency Reconnaissance and Prediction for Non-cooperative Communication Network
- Passive Localization of Multiple Sources Using Joint RSS and AOA Measurements in Spectrum Sharing System
- Specific Emitter Identification for IoT Devices Based on Deep Residual Shrinkage Networks
- Primary User Adversarial Attacks on Deep Learning-Based Spectrum Sensing and the Defense Method

