考虑应力路径基坑变形计算及支护性能研究
牛建东,李泽玮,肖剑,王克宏
考虑应力路径基坑变形计算及支护性能研究
牛建东1,李泽玮1,肖剑2,王克宏3
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 长沙市规划勘测设计研究院,湖南 长沙 410007;3. 湖南省核工业地质局三〇三大队,湖南 长沙 410119)
基于半无限大弹性空间在条形荷载作用下应力的Melan解,首先根据基坑开挖过程应力状态的变化,建立基坑开挖问题的平面力学分析模型。利用Duncan-Chang曲线模型中的参数计算方法,推导加载和卸载模量公式,进而结合平面应变问题的物理方程和几何方程,建立平面应变问题的本构方程,得到基坑开挖后土体位移计算方法。然后建立土压力与支护结构位移的正弦和幂函数关系曲线,提出土压力计算方法。最后将理论成果应用于工程实践,将土体位移和土压力的理论值与实测数据进行对比分析。研究结果表明:该计算模型得到的基坑变形位移与实测结果吻合较好,验证了土压力与位移计算方法的合理性,同时由监测数据得到锚索预应力随时间的三阶段变化趋势,以及深层水平位移和坡顶竖向位移的匙形分布 特点。
深基坑;Melan解;应力路径;位移;土压力;实测数据
近年来,随着城市建设的快速发展,大量的深基坑开挖都分布在城市中心建筑物比较密集的地区。基坑开挖的本质就是土体的卸载,因此必然伴随着地层应力的重分布,从而使基坑土的物理力学性质发生比较大的变化,其中最明显的是土体模量的变化。庄心善等[1]对侧向卸荷条件下土体的力学性能进行了真三轴室内试验,推导了基坑土体侧向卸载切线剪切模量的计算公式,能够较真实地反映开挖卸荷条件下土体的应力−应变特性。路德春等[2]结合土的黏聚强度特性,将子午面划分为硬化区和硬化区,建立了考虑黏聚效应的黏土应力路径本构模型。孙华圣等[3]通过有限元分析,研究了土体杨氏模量对于基坑开挖卸荷引起临近隧道的变形特点,结果表明随着杨氏模量变化,基坑及临近隧道的变形均有较大的变化。HUANG等[4]利用淤泥质土和粉质土进行常规三轴压缩试验和Ko固结卸荷试验,研究了不同应力路径下土体的切线模量,得到了土体的变形特征。刘国彬等[5−7]考虑应力路径,得到了上海及武汉地区的几种典型软土的卸载变形模量与应力路径的表达式,进而研究了开挖卸荷引起地铁隧道的位移预测方法,但是在考虑位移时,并没有考虑土压力随支护结构位移的变化。时俊等[8]考虑土体侧向卸荷对基坑变形的影响,利用土的侧向卸荷应力应变关系,改进了基于塑性变形机制的可发挥强度设计(MSD) 法,探讨了不同应力路径下的基坑变形。由于基坑支护结构与土体的变形是协调一致且在动态变化的。所以在考虑作用于支护结构上的土压力时,就要考虑支护结构的位移,其处于静土压力与极限土压力之间。李连祥等[9]通过考虑基坑支护结构的变形产生的土拱效应以及基坑支护与土体间的摩擦力的作用,提出了修正的朗肯土压力理论,实例验证结果表明修正后的朗肯土压力更接近实际的土压力分布。PENG等[10]假设土体为线性弹簧和刚塑性体的组合体,提出了考虑挡墙变位和位移影响的被动土压力计算方法。易南概等[11]分析了土压力与支护结构位移的一般规律,将作用于基坑支护结构上的土压力和支护结构的侧向位移曲线用双曲线函数表示,建立了基于支护结构侧向位移的土压力计算公式,并且经过计算分析,该公式得到的土压力值与工程实际值比较符合。因此,目前对于基坑过程中支挡结构土压力变化规律的研究还不完善,而实际上作用于支护结构上的土压力分布是十分复杂的,所以用传统的土压力计算方法对基坑的设计计算是不准确的[12]。综上所述,当前的基坑开挖变形计算中,最常用的是用数值模拟法和经验估计法,缺乏一种合理的理论计算方法。而且开挖过程中,往往没有考虑开挖卸荷对土体参数的影响,同时也没有考虑支护结构变形对土压力的影响。前者影响土体模量的变化,后者起着保持土体处于被动荷载状态的作用,且土压力与支挡结构的位移也存在一定非线性关系。基于以上背景,本文通过理论分析,建立了基坑开挖过程中土体的力学分析模型,推导了土体的加卸载模量公式。同时将该理论成果成功应用于长沙市某基坑工程中,通过理论计算和实测结果进行对比,验证了理论模型和计算方法的合理性,最后总结了基坑开挖的变形规律,为类似复杂深基坑的设计和施工提供参照。
1 考虑应力路径的理论模型
基坑开挖过程中,开挖面以下土体竖向卸载明显,导致基坑底部土体回弹变形。随着开挖深度的增加,坑内土与坑外土的高度差增大而产生的荷载效应,加上地面超载,将使基坑外土体和支护结构向坑内移动,导致基坑外土体沉降,而基坑内土体隆起。同时,由于支护结构的变形,基坑周围一定范围内的土体处于挤压荷载作用下。因此,基坑开挖过程中,土体变形模量随时间和空间呈非线性变化。在以往的研究中,学者们往往忽略开挖过程中荷载变化对土体变形模量的影响,从而对计算结果产生一定的误差。
1.1 加载卸载模量

按照Duncan-Chang模型的推导思路,分别得到侧向卸载和轴向卸载条件下的切线弹性模量公式[13],即:
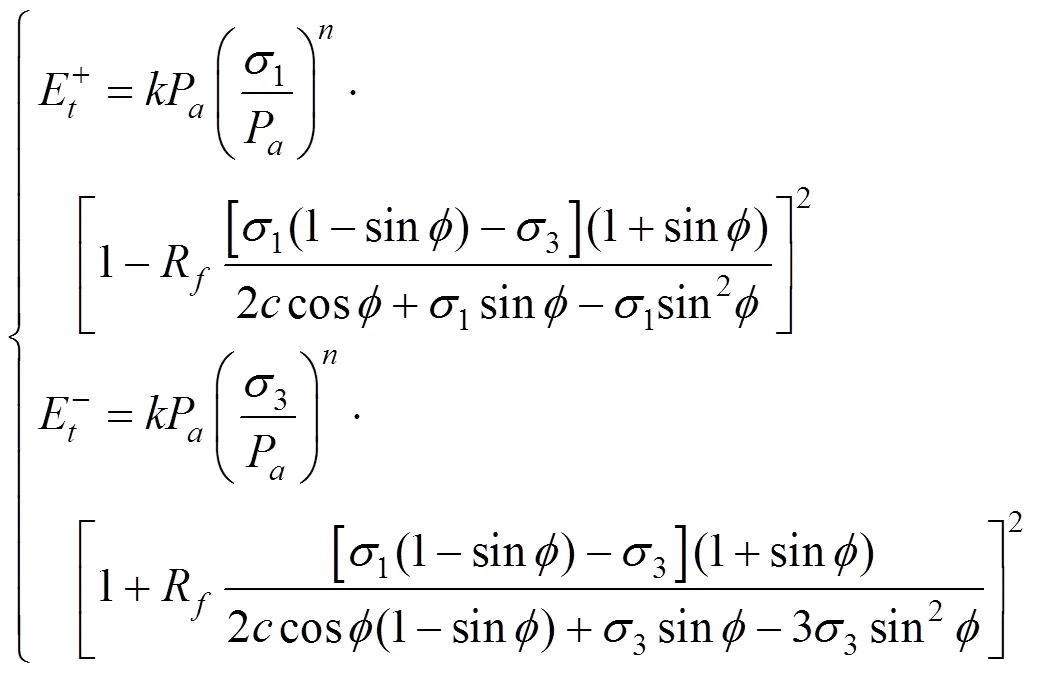
式中:R是破坏比,可以通过常规三轴试验得到;1和3分别是基坑开挖时的最大主应力和最小主应力。和是强度指标,假设不同应力路径下的强度指标一致。P是大气压力,和是常数。
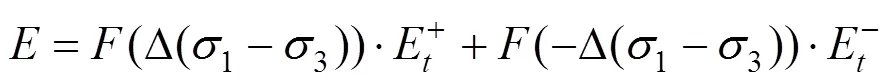
式中:()是单位阶跃函数。当>0时,()=1;当<0时,()=0。
此外,在开挖过程中,土体密度和体积也会发生相应的变化,导致土体泊松比也进一步变化。因此,在基坑开挖过程中土的泊松比的变化可以表示为:
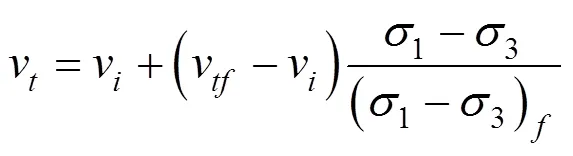
式中:vi为初始切泊松比;vtf为破坏时切线泊松比。
将基坑开挖看作平面应变问题求解,可以得到本构模型:
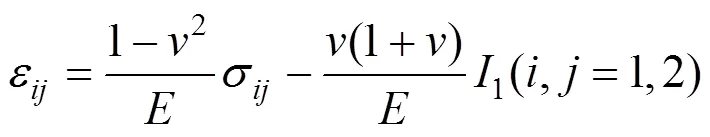
式中:和由式(2)和式(3)得到。
1.2 考虑加卸载的基坑开挖变形分析
对于条形基坑通常将其视为半无限空间中的平面应变弹性问题,如图2所示。基坑开挖后,假设土体对支护结构施加侧压力分别为0和P,支护结构对土体施加侧压力也为0和P。将基坑均分为左右两侧,不考虑左侧和右侧的相互作用(图2(a))。基坑内外空间以支护结构为边界,划分为2个独立区域(图2(b)),此时这2个区域的空间状态变为非半无限空间状态。在支护结构两侧分别施加一个虚拟荷载使得其上作用力变为2P和20时,可以将其扩展成2个独立的半无限弹性空间(图3(c))。
假设材料有相同的模量,Melan提出了在半无限弹性空间中深度为的任意点处施加线性水平荷载的应力分量:
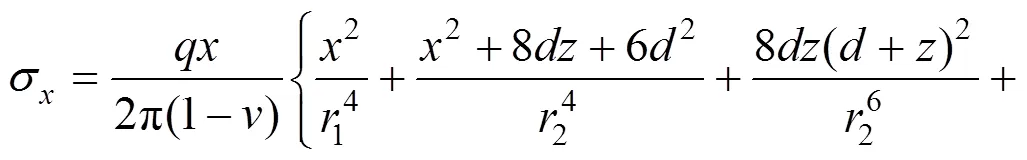
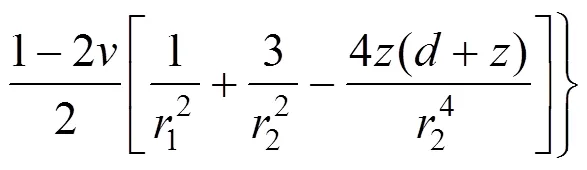
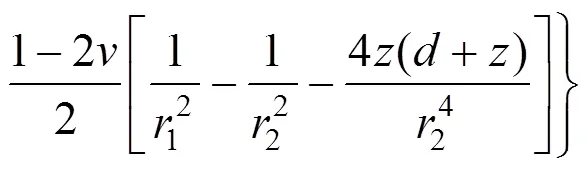
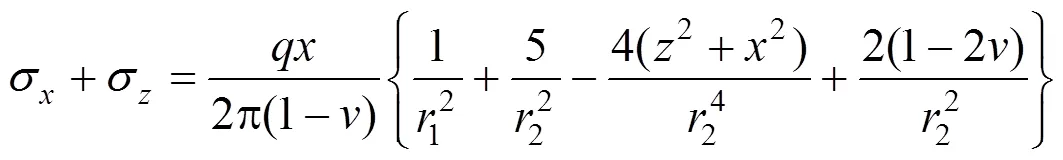
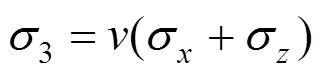
在弹性半无限空间内,作用有一个方向的宽度为的条形荷载,如图3所示,则通过对Melan解积分,该区域内任意一点的应力解:

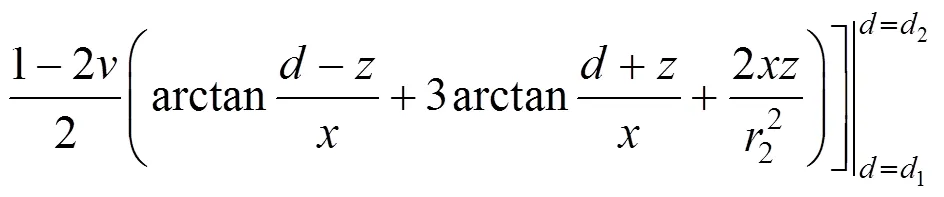
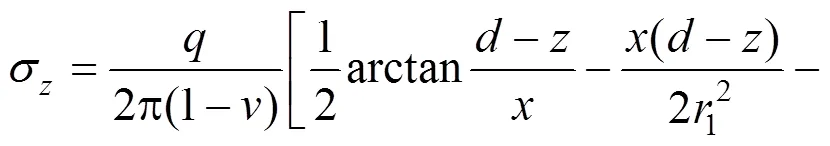
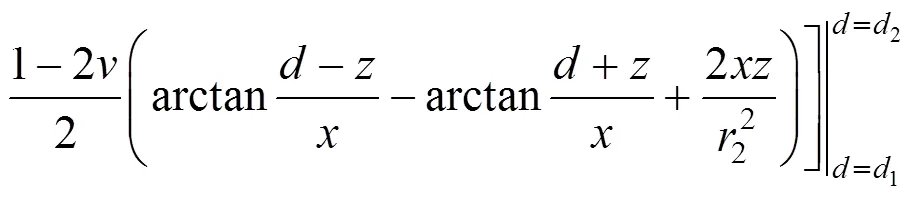
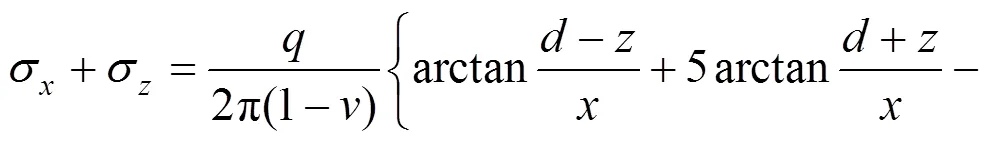
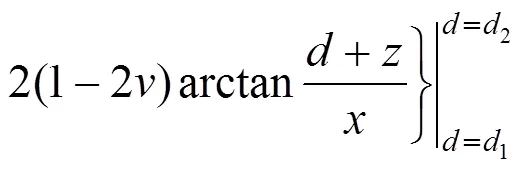
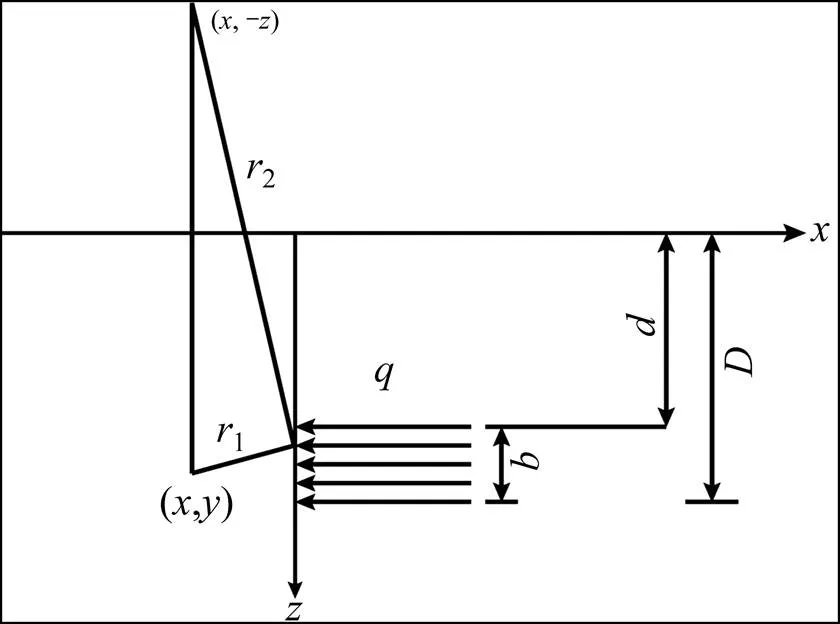
图3 条形荷载作用下的Melan解
对于各向同性平面应变问题,物理方程和几何方程分别为:

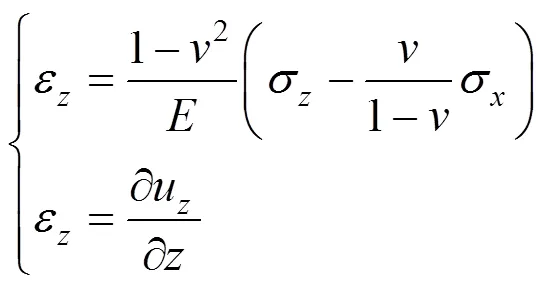
式中:为弹性模量;为材料的泊松比,两者均为考虑土体的应力路径的弹性常数,由式(1)和(3)确定。
当根据式(11)和式(12)求解基坑周围土体变形时,必须确定如图4所示的积分范围,在对称开挖当中,水平积分范围在基坑内是有限的:
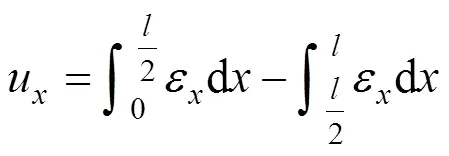
式中:为基坑开挖宽度。
理论上变形影响区在基坑外是无限的,其计算宽度的确定参照条形基础下垫层厚度的确定方法。计算地基沉降压缩深度时,当附加应力降至自重应力的10%时,定义此深度为压缩深度。假定侧向应力降至水平荷载的10%时,土的侧向变形影响范围满足计算要求。根据式(7)中应力解的计算结果,当附加水平应力为水平荷载的10%时,对应的距离约为荷载宽度的10倍。因此,基坑外影响区定义为10倍的基坑深度,则基坑侧壁水平方向位移:
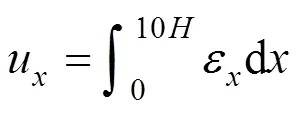
同理,基坑垂直方向的位移为:

式中:为基坑开挖深度。
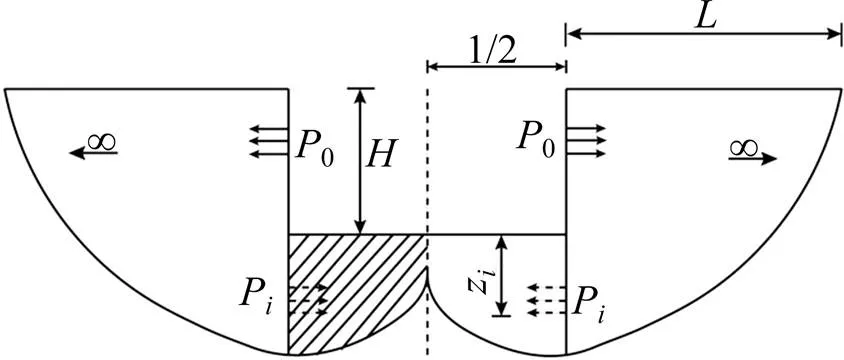
图4 基坑边界条件
1.3 与位移有关的土压力计算
支护结构位移的变化导致土压力的变化,图5给出了土压力随支护结构位移的变化。其中,横坐标Δ/代表支承结构的位移和墙高之间的比值。+Δ/代表支护结构朝向土体移动,−Δ/代表支护结构远离土体移动。
当支护结构位移为零时,这时作用在支护结构上的土压力为静止土压力0。当支护结构远离土体达到极限位移时,主动土压力为E,当支护结构朝向土体达到极限位移时被动土压力为E。在极限位移以外的情况下,土压力介于这三者之间,取决于支护结构的位移。因此,在计算土压力时应考虑开挖引起的支护结构位移的影响。
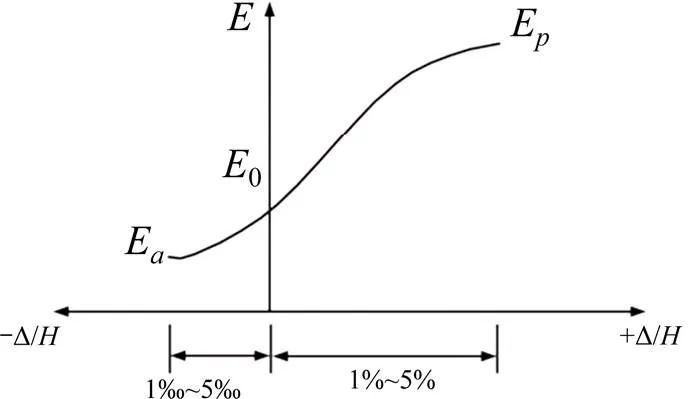
图5 土压力随位移的变化
本文用正弦和幂函数组成的复合函数表示与位移相关的土压力计算方法:
其主动土压力:
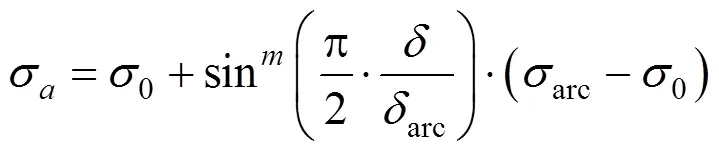
被动土压力:

式中:0是静止土压力;是土的位移(取正值);acr土的主动极限位移;pcr是土的被动极限位移;acr是极限平衡状态的主动土压力和pcr极限平衡状态的被动土压力;为支护系数,随支护结构刚度、土体的性质及开挖深度有关,取0~1,当基坑参数及支护结构等越不利于基坑稳定时,取上限。
由式(16)~(17),如果土体位移等于主动极限位移acr,计算得到的土压力就是主动极限土压力acr;如果土体位移等于被动极限位移pcr,计算得到的土压力就是主动极限土压力σpcr。
2 案例分析
2.1 工程概况
为验证该理论在实际工程中的实用性和可靠性,将理论成果应用于长沙某基坑工程,并与开挖实测数据进行对比。工程位于长沙市天心区,基坑长110 m,宽38 m。最大开挖深度16.3 m,是中部地区典型的边坡+基坑形成的深基坑,基坑周边环境条件复杂。
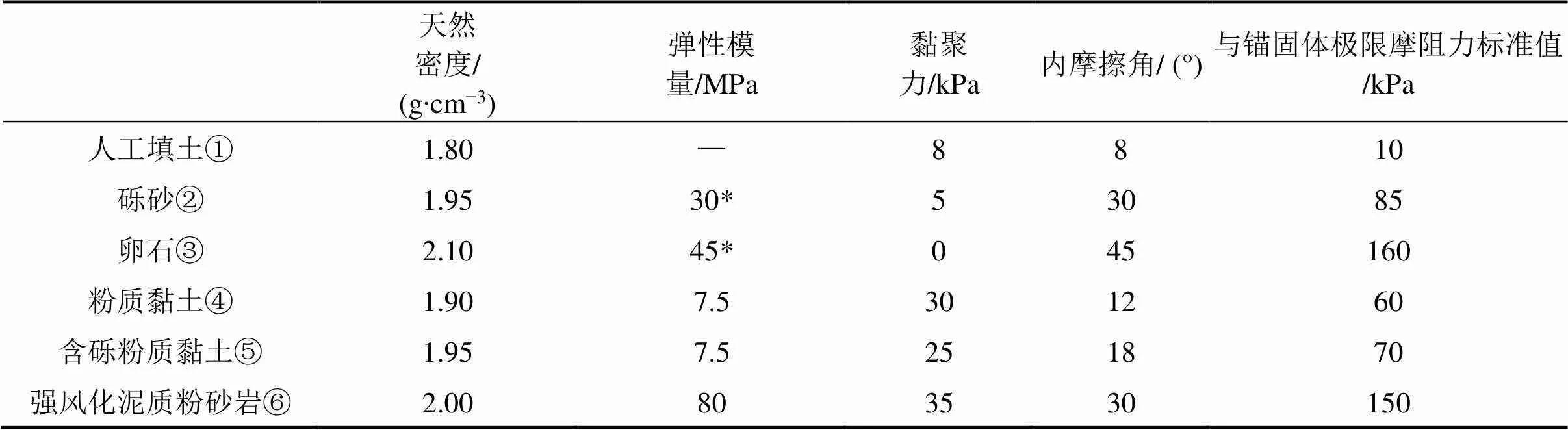
表1 土层参数
注:表中带“*”号者为变形模量。
场地地层条件为软硬地层交替存在,主要由人工填土、厚层砂卵石层,以及下部强风化粉砂岩组成。其中人工填土层厚度较大,平均可达7.4 m,工程性质较差。地下水主要为潜水,孔隙潜水主要赋存于砾砂和卵石层中,不具承压性,基坑开挖前已采取排水措施。表1为场地土层参数随深度的变化。为便于计算,将分层土视为均质土,即取土体参数的平均值。假定土体为连续介质,不考虑土体的破坏。
2.2 基坑支护形式
由于该深基坑工程距离周边临近建(构)筑物很近,基坑的施工空间受限,而且对施工扰动和噪音的要求较高,同时还要严格控制基坑的变形位移。最终采用“预应力桩锚”支护方案。
上部−2~0 m,采用放坡挂网喷砼支护,可以适当减小上部土体荷载。
下部−13.2~−2 m,采用桩锚支护,由桩顶处沿竖向布置6排锚索。支护桩采用人工挖孔桩,桩长22.7 m,桩径1.2 m,桩间距2 m。锚索长度25 m,成孔角度25°,锚索拉力锁定值360 kN。支护典型剖面图如图6所示。

单位:mm
2.3 计算结果分析
图7和图8分别给出了基坑周围地表沉降和坑壁侧向位移的理论值和实测值。本文计算模型得到的结果与现场实测数据基本吻合。实测得到的基坑周围地表最大沉降量为16.23 mm,距基坑边缘8 m,理论计算最大沉降量为11.52~13.24 mm,距坑壁6.2 m。同时基坑底部越靠近基坑中心,隆起量越大,考虑卸载模量的基坑隆起最大值达到27.43 mm,与实测值33.20 mm一致。图8中,考虑加载和卸载的基坑侧壁水平位移最大值为15.65 mm,实际监测值为12.20 mm。可以看出理论计算结果均小于实测值,可能是理论计算模型没有考虑基坑周围超载对变形的影响,以及将基坑假定为平面应变弹性体的原因。将位移的计算值代入式(11)和式(12),得到开挖后的土压力,如图9所示,其处于静止土压力和主动土压力之间。
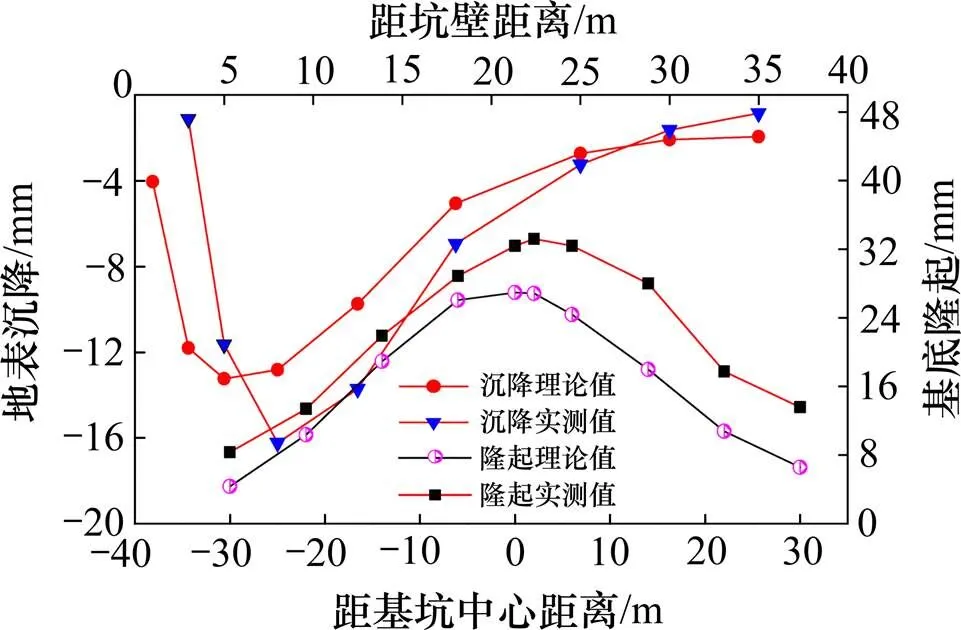
图7 基坑周围土体竖向位移对比
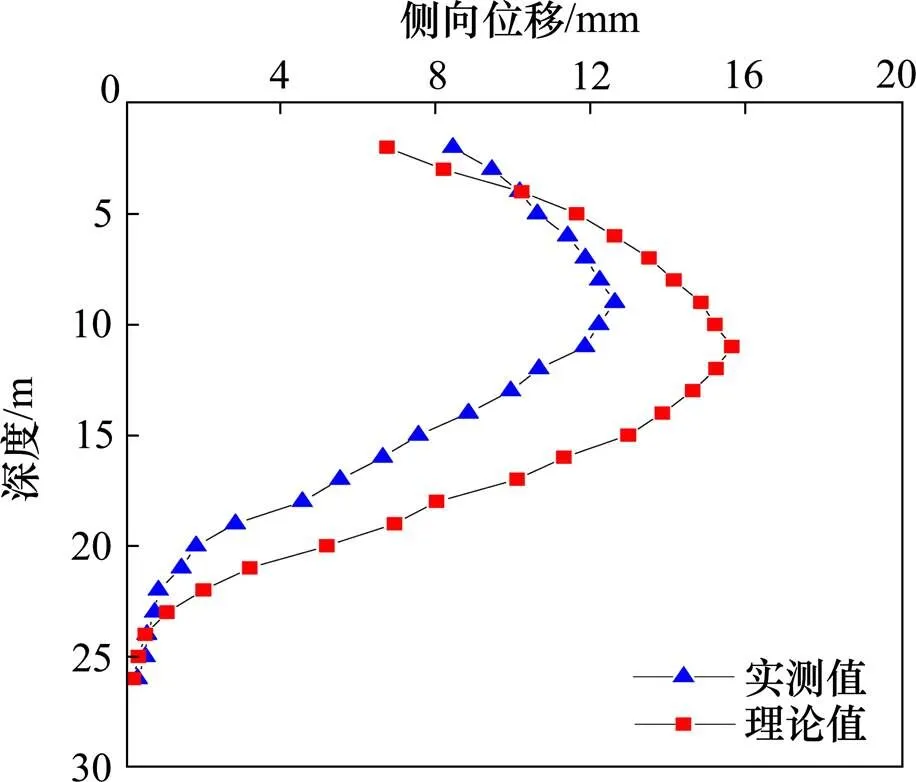
图8 基坑侧壁水平位移对比

图9 基坑周围土体的侧向压力
3 实测数据分析
3.1 锚索内力的监测数据分析
图10为锚索在工作阶段轴力沿轴向分布情况,可以看出锚索的内力分布在自由端处最大,越往锚索末端迅速衰减,整体分布规律为指数形式[16]。
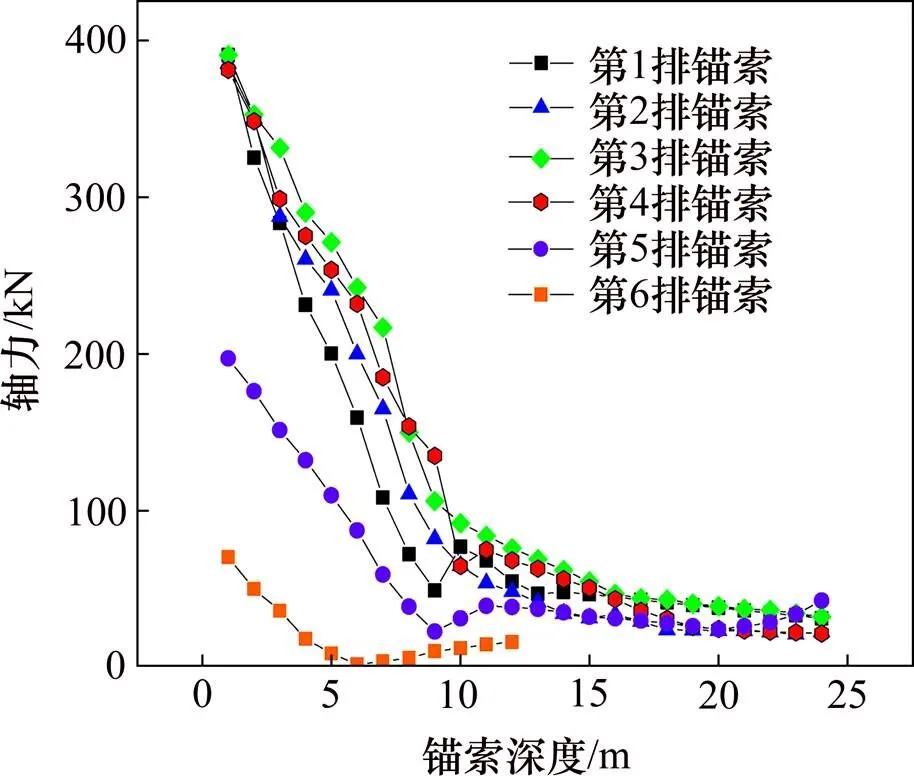
图10 锚索工作阶段轴力沿锚索轴向分布
图11给出了锚索自由段处预应力随时间的变化情况。通过监测结果可以看出,锚索预应力随时间的发展趋势大致分以分为3个阶段,其最大损失10.53%。其中第1个阶段是预应力的快速损失阶段,其锚固力下降是最快的,在5 d时间里损失率达到4.1%,约占总的锚固力损失的一半,影响因素主要是钢绞线的松弛和周围土体变形等共同作用的结果。第2阶段是预应力的波动阶段,从第1阶段结束到第45 d左右,第2阶段预应力下降缓慢但是持续时间较长,平均损失总量达到约8.5%。第3阶段为自锚索锁定约第45 d后,为基本稳定阶段,该阶段以后,锚索的锚固力变化不明显,如表2所示。
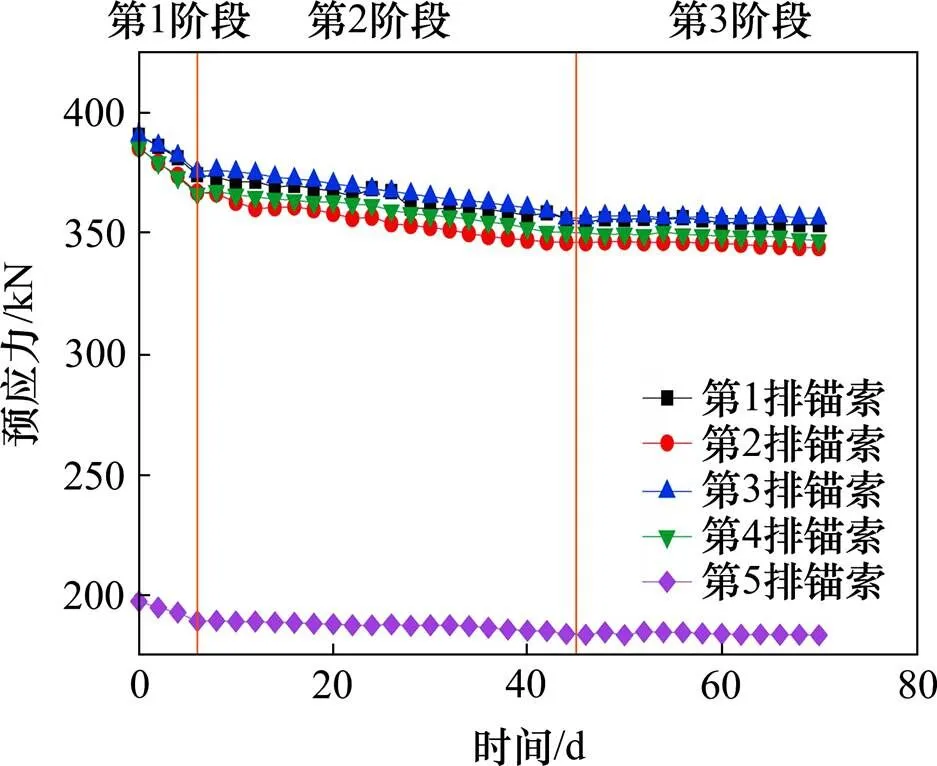
图11 锚索预应力随时间变化曲线

表2 锚索各阶段预应力损失
3.2 深层水平位移监测数据分析
图12给出了支护结构在不同开挖阶段水平位移的实测值。支护结构的侧向位移沿开挖深度的增加而逐渐增大,最终在开挖深度为7~11 m时达到最大值,之后位移逐渐减小,最大为11.3 mm,与基坑开挖深度16.3 m相比,约占0.072%,水平位移沿深度的总体分布为匙形。最大位移出现的位置也随着开挖深度的进行而逐渐下移,但始终在开挖面以上,这是因为预应力锚索有效限制了桩体上部的变形,而坑底土体又有效地限制了嵌固深度内桩体的位移,与计算结果基本吻合。在工程实际应用中为了能够更加有效地控制基坑水平变形,在支护结构的中部位置应适当进行加固处理。
3.3 坡顶沉降监测数据分析
图13给出了基坑分步开挖过程中的坡后土体沉降位移曲线,坡后土体的位移沉降变形呈现先增大后减小的趋势,监测数据表明,地表沉降发生在距基坑一定距离的范围以内。随着基坑开挖的进行,坡后土体的沉降增幅不断加大,最大位移增幅为3.98 mm,相对于前一步位移增幅提高了77.73%,基坑开挖完成后的最大沉降位移为13.24 mm,与基坑开挖深度相比,约占0.081%。在开挖初期第1个阶段,受开挖卸荷的影响,基底发生垂直的弹性隆起,由于支护结构底部为注浆加固土体,回弹抬高,使得第1阶段地表沉降量偏小,甚至出现隆起。结果表明,基坑开挖对周围土体沉降的影响仅限于距基坑30 m范围内,超过30 m时,这种影响可以忽略不计,最终的最大沉降约为13 mm。

图12 各开挖阶段侧向位移随深度的变化
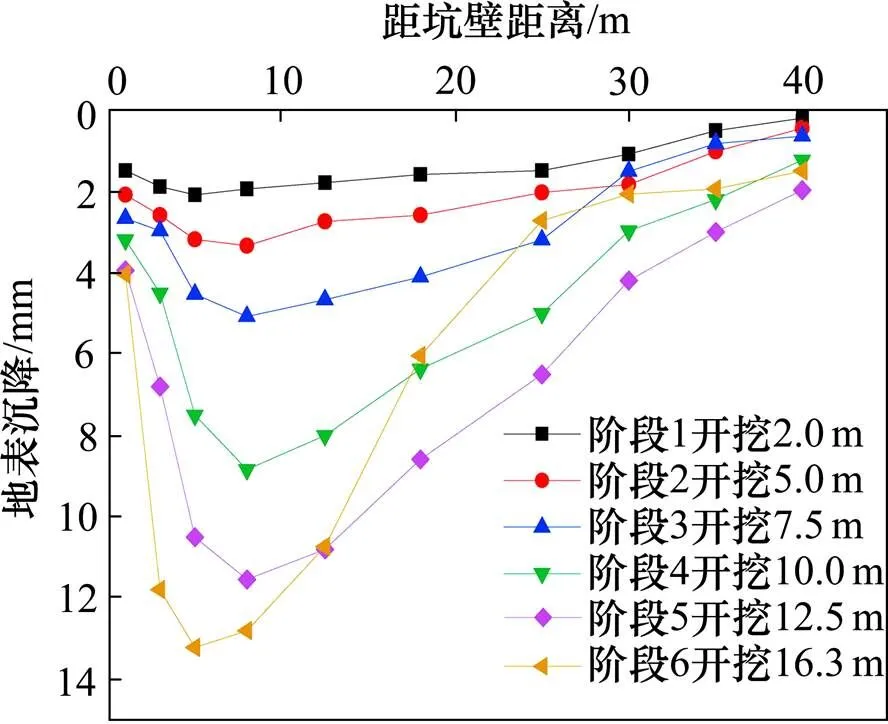
图13 各开挖阶段竖向位移随距坑壁距离的变化
在开挖初期,基坑开挖卸载对竖向位移的影响大于对水平位移的影响,但随着开挖深度的增加基坑开挖对基坑竖向位移的影响减小而对基坑水平位移的影响却明显增大,这是由于开挖深度的增加,基坑内外高度差形成的加载不断增大的原因。
4 结论
1) 根据基坑开挖过程中土体的实际应力状态,得到考虑应力路径的加、卸载模量,并对基坑周围土体的变形计算进行了修正。将理论成果应用到实际工程中,验证了计算模型和分析方法的合理性。
2) 通过考虑作用于支护结构上的土压力与位移相关,建立正弦函数关系来修正经典朗肯土压力公式。结果表明,经修正的土压力公式能更好的反映支护结构上的土压力分布情况。
3) 锚索发挥作用后轴力沿轴向呈现非线性分布特点。锚索预应力随时间的变化分为快速下降、波动变化和趋于稳定变化的3个阶段。基坑水平位移随开挖深度的增加呈先增大后减小的变化趋势,随开挖阶段位移逐渐增大,并且最大位移出现的位置也逐渐下移。坡后竖向位移与距坑边距离在一定范围内也呈现匙形分布,超过30 m范围影响可忽略不计。
[1] 庄心善, 朱志政, 朱瑞赓, 等. 基坑土体卸荷剪切模量真三轴试验研究[J]. 工业建筑, 2005, 35(7): 55−58, 66. ZHUANG Xinshan, ZHU Zhizheng, ZHU Ruigeng, et al. Study on true triaxial test of excavation soil mass of unloading shearing modulus[J]. Industrial Construction, 2005, 35(7): 55−58, 66.
[2] 路德春, 程志亮, 林庆涛, 等. 考虑黏聚效应的黏土应力路径本构模型[J]. 北京工业大学学报, 2019, 45(9): 859−869. LU Dechun, CHENG Zhiliang, LIN Qingtao, et al. Complex stress paths constitutive model for clay considering the effect of cohesion[J]. Journal of Beijing University of Technology, 2019, 45(9): 859−869.
[3] 孙华圣, 匡铁生, 张继华, 等. 土体杨氏模量对开挖卸荷引起隧道变形影响[J]. 淮阴工学院学报, 2019, 28(1): 31−35. SUN Huasheng, KUANG Tiesheng, ZHANG Jihua, et al. Effect of soil Young's modulus on tunnel deformation due to stress relief[J]. Journal of Huaiyin Institute of Technology, 2019, 28(1): 31−35.
[4] HUANG Hua, HUANG Min, DING Jiangshu. Calculation of tangent modulus of soils under different stress paths[J]. Mathematical Problems in Engineering, 2018(2018): 1−11.
[5] 刘国彬, 侯学渊. 软土的卸荷模量[J]. 岩土工程学报, 1996, 18(6): 18−23. LIU Guobin, HOU Xueyuan. Unloading modulus of the Shanghai soft clay[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(6): 18−23.
[6] 刘国彬, 侯学渊. 软土的卸荷应力—应变特性[J]. 地下工程与隧道, 1997(2): 16−23. LIU Guobin, HOU Xueyuan. Unloading stress-strain characteristics of soft soil[J]. Underground Engineering and Tunnels,1997(2): 16−23.
[7] 刘国清, 宁国立, 陈厚仲, 等. 武汉软土的卸荷应力—应变归一化特性研究[J]. 建筑科学, 2012, 28(3): 46− 49. LIU Guoqing, NING Guoli, CHEN Houzhong, et al. Study on stress-strain normalization of soft soil under excavation unloading in Wuhan area[J]. Building Science, 2012, 28(3): 46−49.
[8] 时俊, 万磊, 谭卫佳, 等. 考虑土体侧向卸荷的基坑变形预测[J]. 河南科技大学学报(自然科学版), 2020, 41(2): 61−66. SHI Jun, WAN Lei, TAN Weijia, et al. Deformation prediction of excavation of lateral unloading soil[J]. Journal of Henan University of Science and Technology (Natural Science), 2020, 41(2): 61−66.
[9] 李连祥, 王兴政. 考虑基坑支护结构变形模式的土压力研究[J]. 地下空间与工程学报, 2018, 14(4): 1024− 1033. LI Lianxiang, WANG Xingzheng. Research on earth pressure considering deformation pattern of foundation pit supporting structure[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(4): 1024− 1033.
[10] PENG Shuquan, LI Xibing, FAN Ling, et al. A general method to calculate passive earth pressure on rigid retaining wall for all displacement modes[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(6): 1526−1532.
[11] 易南概, 吴大群, 谢志, 等. 基于支护结构位移计算土压力的方法[J]. 沈阳建筑大学学报(自然科学版), 2005, 21(1): 26−28. YI Nangai, WU Daqun, XIE Zhi, et al. A method of lateral earth pressure calculation consequent upon displacement for excavation[J]. Journal of Shenyang Architectural and Civil Engineering Institute, 2005, 21(1): 26−28.
[12] 陈奕柏, 柯才桐, 高洪波, 等. 考虑变位影响的刚性挡墙非极限土压力研究[J]. 岩石力学与工程学报, 2015, 34(5): 1060−1070. CHEN Yibai, KE Caitong, GAO Hongbo, et al. Non-limit state earth pressure against retaining wall considering influence of deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 1060−1070.
[13] 殷德顺, 王保田, 王云涛. 不同应力路径下的邓肯−张模型模量公式[J]. 岩土工程学报, 2007, 29(9): 1380− 1385. YIN Deshun, WANG Baotian, WANG Yuntao. Tangent elastic modulus of Duncan-Chang model for different stress paths[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1380−1385.
[14] HUANG Ming, LIU Xingrong, ZHANG Naiyang, et al. Calculation of foundation pit deformation caused by deep excavation considering influence of loading and unloading[J]. Journal of Central South University, 2017, 24(9): 2164−2171.
[15] 张永兴, 丁敏, 王辉. 基于Melan解的地下连续墙结构分析方法[J]. 岩土力学, 2012, 33(10): 2890−2896, 2978. ZHANG Yongxing, DING Min, WANG Hui. Analysis method for diaphragm wall structure based on Melan's solution[J]. Rock and Soil Mechanics, 2012, 33(10): 2890−2896, 2978.
[16] 景锋, 成传欢, 余美万, 等. 锚索内锚段荷载分布及其随时间变化规律[J]. 长江科学院院报, 2011, 28(5): 50− 54. JING Feng, CHENG Chuanhuan, YU Meiwan, et al. Load distribution and the law of its variation in the inner segment of prestressed anchor cable[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(5): 50−54.
Deformation calculation and supporting performance of foundation pit considering stress path
NIU Jiandong1, LI Zewei1, XIAO Jian2, WANG Kehong3
(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Changsha Planning & Design Survey Institute, Changsha 410007, China;3.303 Brigade of Hunan Nuclear Geology, Changsha 410119, China)
Based on the Melan’s solution of stress and displacement of semi-infinite elastic space under strip load, the plane analysis model of foundation pit excavation was established according to the change of stress state in the excavation process. By using the parameter calculation method of Duncan-Chang curve model, the modulus formula was deduced. Then, the calculation method of soil displacement after foundation pit excavation was established by combining the physical equation and geometric equation of plane strain problem. The curve of sine and power function between earth pressure and displacement of supporting structure was established and the method of calculating earth pressure was proposed. Finally, the theoretical results were applied to engineering practice, the theoretical value and the measured data were compared and analyzed, and the deformation law of foundation pit excavation was summarized. The results show that the deformation of the pit obtained by the calculation model are in good agreement with the measured results, and the rationality of the calculation method of earth pressure and displacement is verified. At the same time, the monitoring data shows the three-stage trend of anchor cable prestress with time is obtained, as well as the spoon shape distribution characteristics of the deep horizontal displacement and the vertical displacement of the slope top.
deep pit; Melan’s solution; stress path; displacement; earth pressure; measured data

TU470
A
1672 − 7029(2021)01 − 0071 − 10
10.19713/j.cnki.43−1423/u.T20200270
2020−04−06
国家自然科学基金资助项目(51778634)
肖剑(1977–),男,湖南长沙人,高级工程师,从事岩土工程勘察、设计和检测方面的研究;E−mail:1581546668@qq.com
(编辑 涂鹏)

