故障及经济相关下动车组系统动态成组维护策略

杨国军，王红，何勇，熊律，王宏宇

故障及经济相关下动车组系统动态成组维护策略

杨国军1, 2，王红1，何勇1，熊律1，王宏宇1

(1. 兰州交通大学 机电工程学院，甘肃 兰州 730070；2. 中车戚墅堰机车车辆工艺研究所有限公司，江苏 常州 213011)

为探究不同运量需求影响下动车组复杂系统成组维护策略，基于故障链理论分析部件间故障传递过程，建立故障相关影响下部件可靠度衰退模型。引入运量需求因子描述动态运量需求，建立考虑运量需求的部件维护调整成本模型，基于动态成组方法对部件维护活动进行合并，构建考虑运量需求的动车组复杂系统动态成组模型。算例结果表明：考虑故障相关性对可靠度评估更为科学，同时动态成组方法可以较好的适应运量需求，能够进一步提升动车组系统维修经济性。

动车组系统；故障相关性；经济相关性；动态成组；预防性维护

我国高铁客流呈季节性变化[1−2]，不同客流需求下动车组上线需求不同，为避免运维计划干扰，维护计划随用车需求进行动态调整有利于降低运维成本。同时动车组系统为复杂耦合系统，部件衰退过程存在故障相关性，维修活动间存在经济相关性，若制定维护策略时忽略部件间故障、经济相关性将不利于其准确制定与可靠建模[3]。成组维护是多部件系统维护的重要方法之一，目前的静态成组方法并不能适应不同时段内运量需求变化，而动态成组方法将系统生命周期划分为一系列短期维修决策区间，通过决策区间不断滚动更新获得时变工况影响下的动态成组方案[4−5]。但现有的动态成组策略多与经济相关性结合[6−7]，对部件间的故障相关性研究常见于静态成组策略研究[8]。符杨等[9]提出了一种基于couple函数的故障相关分析方法，但当系统部件较多时解析模型较为复杂。葛小凯等[10]基于依赖概率矩阵对部件间的复杂相关性进行了研究，对历史故障数据的依赖性较高。而故障链理论能较好的分析复杂系统内部件间故障传播过 程[11]，有利于系统内部件可靠度准确建模。综上，目前的动态成组策略与故障相关性结合较少，同时并未考虑到运行计划变化引起的复杂系统动态成组方案调整。为此，本文基于故障链理论分析部件间的故障传播关系，构建故障相关影响下部件可靠度模型。建立匹配动态运量需求的动车组系统动态成组维护策略，以避免成组维护在客流高峰期进行，提升动车组系统维修经济性。

1 问题描述与假设

动车组运量需求在时域范围内动态波动，部分区间内运量需求极大(如春、暑运)。维护活动发生于需求高峰期时将造成较大的停机损失，若提前送修将会浪费系统使用价值，而延迟维修则会提升其失效风险。此外，动车组系统作为复杂耦合系统，维护活动成组归并时充分考虑故障、经济相关性能够提升可靠度及成本评估的准确性。

本文以多部件系统维护节省成本为优化目标，建立故障、经济相关影响下的动车组系统动态成组模型。基于研究内容，假设如下：

1) 部件初始可靠度为“1”，即从全新投入使用；

2) 部件的故障里程服从尺寸参数为，形状参数为的两参数威布尔分布；

3) 部件合并维修时停机维修时间不发生变化；

4) 系统的维修资源充足，各种故障都能被及时修复，不考虑维修资源不足引起的维修等待。

5) 由于维修合并时维修资源可以共享，因此维修组合只需单个部件的维修资源准备成本。

2 可靠度模型建立

2.1 部件固有故障率建模

威布尔分布能够较好的描述机械零部件衰退过程，被广泛应用于部件故障率建模。根据假设(2)，部件的固有故障率如式(1)所示：

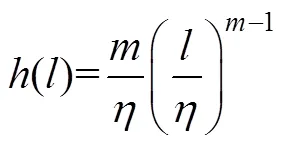
式中：为部件当前服役里程；，分别为威布尔分布形状、尺寸参数。

当不考虑维护活动影响时，部件失效过程如式(1)所述。但维护活动对部件“健康”状态具有改善作用，根据ZHOU等[12]提出的混合式故障率演化规则，维护前后的故障率具有如下关系：

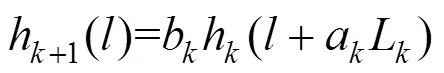
其中：b为故障率递增因子；a为役龄递减因子；L为第个维护周期长度。

2.2 部件相关故障率分析

故障链理论中，对于只影响其他部件的部件称为相关故障起点，只受其他部件影响的部件称为相关故障终点，既受其他部件影响又影响其他部件的部件称为故障中间点[11]。图1所示为包含上述关系的复杂系统单向故障传递过程故障链，其中部件，为相关故障起点，部件，为故障中间点，部件，为相关故障终点。

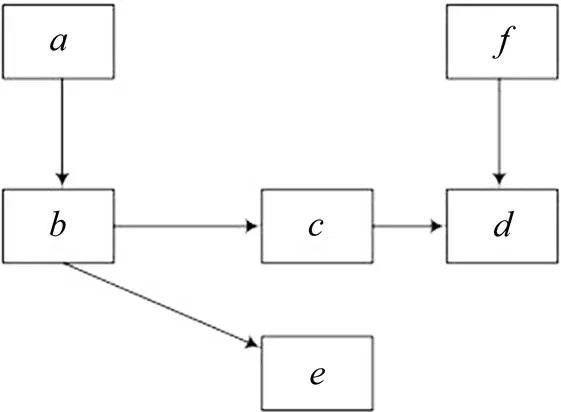
图1 多部件系统单向相关故障链

以图1所示系统为例，按故障层次对部件进行编号。在所有故障链中选出始于相关故障起点，且传递过程最长的故障链，将其称为主故障链，除主故障链外其余故障传递称为故障支链。以相关故障起点为第Ⅰ层，依据部件在故障链中所处位置进行故障层次排序。如图1主故障链内部件故障层次为(Ⅰ)−(Ⅱ)−(Ⅲ)−(Ⅳ)，故障支链故障层次为(Ⅰ) −(Ⅱ)。若从主故障链分支进行排列，则从分支部件进行编号，如(Ⅰ)−(Ⅱ)−(Ⅲ)。同一故障层次内位于主故障链的部件优先进行编号，不同故障层次以其层次排序为依据升序排列。则图1所示系统内部件故障层次及编号结果如表1所示。

表1 部件故障层次及编号

根据表1中的部件故障编号可以明确部件间的故障相关关系，文献[11]中利用故障相关系数量化故障相关程度，则图1所示系统的故障相关系数矩阵为：

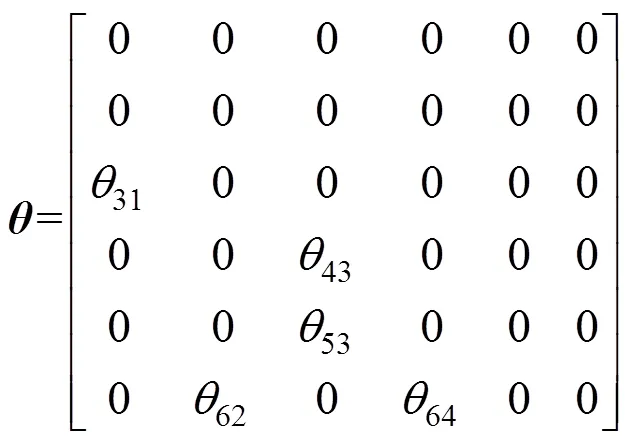
考虑到故障相关关系后，部件的故障率函数由2部分组成：受其余部件故障影响导致的相关故障率及只受自身役龄影响的固有故障率[11]。则考虑故障相关后的部件故障率函数为：

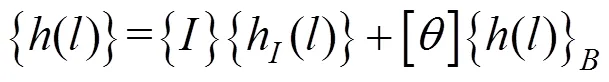
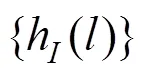
2.3 部件相关可靠度建模

可靠度是可靠度函数的概率表达，而可靠度函数与失效率函数具有以下关系：

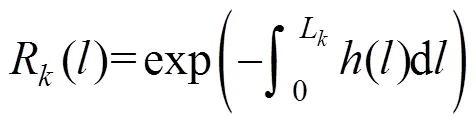
考虑到故障相关后，将式(4)代入式(5)中，则故障相关影响下部件的可靠度变为：

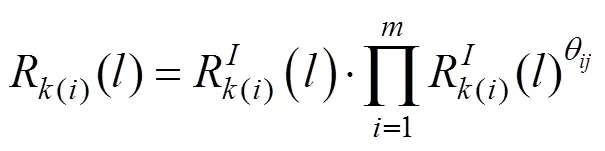
3 动态成组策略及成本建模

不同部件由于其维护参数不同而导致维修周期不尽相同，动态成组维护在部件最优维护周期的基础上进行调整，从而使多个部件维修时刻重合而实现成组维护。本文对传统动态成组方法作了相应改进，详细如下文所述。

3.1 部件维护调整范围

部件进行成组时某些部件会提前维护，这样会浪费设备的使用价值；有些部件需要延迟进行维护，这样会提高其失效风险。提前或延迟维护时的故障维修变动成本由下式计算：

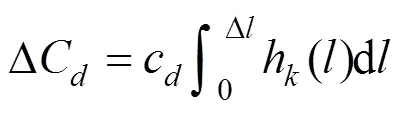
式中：Δ维护提前或者延迟时的里程调整量。另外，提前维修产生的使用价值浪费可由式(8)得到：

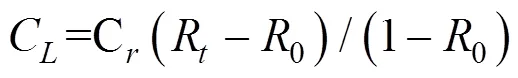
式中：C为部件的可靠度利用价值；R为部件维护提前后的可靠度值；0为部件预防性维护阈值。

图2 不考虑运量需求变化的成组方法

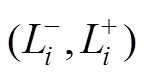
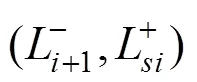
图3 考虑运量需求的成组方法

3.2 多部件系统成组方案

根据3.1节内容，维护调整成本中考虑停机损失波动时表达如下：

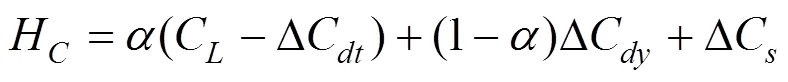
式中：通过提前/延迟维护成本比较来决策取值，当维护活动提前时=1，延迟时=0。ΔC为运量需求引起的停机成本变化，其值由式(10)可得。

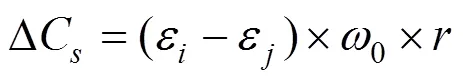
式中：为第次停机维护时的运量需求因子值；0为单辆动车的基准运量；为运量收益因子。

根据3.1节中的成组方法可以获得相应的成组方案。维修组合内实施成组维修的成本收益为：

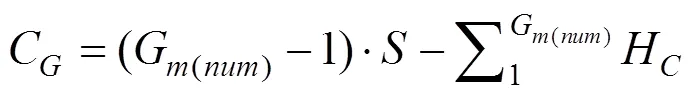
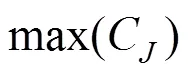
Step 1：优化获得部件最优经济性下的可靠度阈值及维护周期；

Step 2：对部件的维护周期按升序排列，确定最先维护的部件并计算每个部件的维护调整范围；

Step 3：以部件为基准，判断与部件维护调整范围是否存在交集，若存在交集则成组，同时执行Step 4；若交集为空，则执行Step 5；

Step 4：基准部件不变，=+1向前搜索能够成组的部件，直至部件与的交集为空，记录此时维修组合，并基于式(12)求得最优成组点及相应成本，完成后令+1同时返回Step 3；

Step 5：记录当前的维修组基准部件，同时1进行下一基准部件的成组，返回Step 3重复Step 3～5，直至判断完系统内所有部件；

Step 6：不断进行滚动，重复Step 1～5得到系统全寿命周期内的成组计划。

4 算例分析

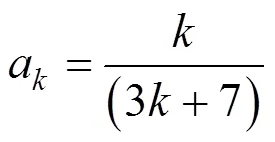
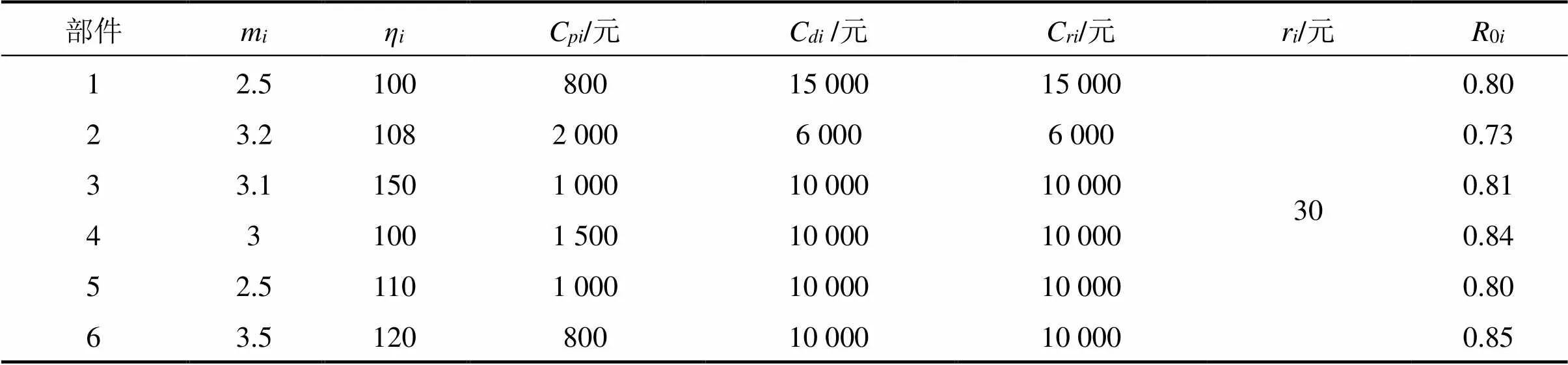
表2 部件维护参数及可靠度阈值

以图1所示系统为例，根据本文2.2节中编号方法其故障相关形式进行编号，确定其相关关系。参考文献[13]中的方法，确定系统内部件的相关系数矩阵如下：

为探究故障相关对部件可靠度演化规律的影响，以部件4为例进行分析。结合图1及表1可知仅有部件3对部件4失效过程产生影响，对部件3和4的固有可靠度及部件4的综合可靠度演化规律分析如图5所示。

由图5可见，部件3衰退过程对部件4的可靠度衰退具有明显影响，并且随着维护活动的进行，综合可靠度与固有可靠度的差值将会逐步增大。此时若仍以固有可靠度为依据计算维护周期引起一定的安全风险。

为量化运量需求在时域范围内动态变化，参考文献[14]中对动态应力的等效方法，对文献[2]中运量数据进行分段等效。这里定义当前运量与基准运量的比值为运量需求因子，运量需求因子及其区间长度如表3所示。

表3 运量需求因子及取值

为探究动态运量及故障、经济相关对成组方案的影响，设计了3种不同的方案：方案1并没有考虑运量需求与相关性；方案2将动态运量需求纳入成本建模中，基于经济相关对维护活动进行合并；方案3综合考虑了运量需求和故障、经济相关对成组策略的影响。

由表3可知，考虑运量需求的方案2较方案1节省成本上升22.9%，明显优于方案1。但方案3相较方案1成本节省并不显著，因此有必要对其方案2和方案3的成组过程进行进一步探讨。

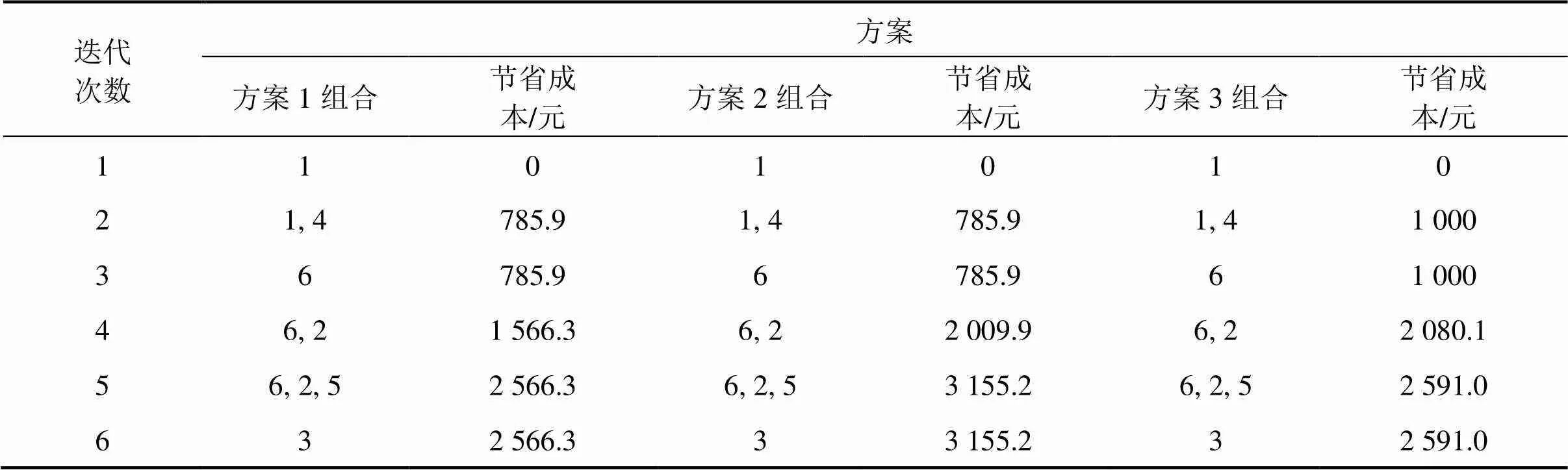
表3 不同策略下部件成组方案及节省成本

表4 优化分组及停机时刻

由表4可见当存在故障相关时，维修组1内部件1，4的维护周期由57，58万km变为58，58万km，2部件维护时刻重合，从而不必进行维护调整就能成组，因此维修节省成本较方案2提升27.2%。而故障相关影响下2中3个部件的维修周期差距较方案2变大，此时进行成组合并时部件维护调整成本更高，因此维修节省成本较方案2降低10.6%。对比维修组1和G2优化结果可知，故障相关性对多部件成组维修合并具有重要影响。

5 结论

1) 与传统动态成组方法相比，考虑运量需求的动态成组方案通过维修调整，避免维护活动在运量需求较大的时刻进行，能够进一步提升动车组系统维修经济性。

2) 故障相关影响下部件衰退过程较不存在故障相关时明显加快。为保障动车组系统安全性，对存在故障相关的系统要防止故障相关传递，如增加部件间的柔性连接等。

3) 故障、经济相关性对部件的维修合并活动存在重要影响，合并维修时充分考虑到故障、经济相关性，能够有效降低多部件维护成本。

[1] 耿立艳, 鲁荣利, 李新杰. 基于波动聚集性的城际高铁客流量预测[J]. 铁道科学与工程学报, 2019, 16(8): 1890−1896. GENG Liyan, LU Rongli, LI Xinjie. Predicting intercity high-speed railway passenger flow based on volatility clustering[J]. Journal of Railway Science and Engineering, 2019, 16(8): 1890−1896.

[2] 李建一. 京沪高铁短期客流量预测及票额分配的优化研究[D]. 保定: 华北电力大学, 2015: 15−20. LI Jianyi. Research on short-term passenger flow volume forecasting and ticket assignment optimization For Beijing-Shanghai high-speed railway[D]. Baoding: North China Electric Power University, 2015: 15−20

[3] Olde Keizer M C A, Flapper S D P, Teunter R H. Condition-based maintenance policies for systems with multiple dependent components: A review[J]. European Journal of Operational Research, 2017, 261(2): 405−420.

[4] 苏春, 陈武. 基于滚动窗口方法的风力机动态机会维修优化[J]. 机械工程学报, 2014, 50(14): 62−68. SU Chun, CHEN Wu. Dynamic opportunistic maintenance optimization for wind turbine system based on rolling horizon approach[J]. Journal of Mechanical Engineering, 2014, 50(14): 62−68.

[5] 罗斌, 林琳, 钟诗胜.飞机多疲劳结构动态成组维修决策优化方法[J]. 控制与决策, 2019, 34(7): 1365−1374. LUO Bing, LIN Lin, ZHONG Shisheng. Dynamic grouping maintenance planning for aircraft with multiple fatigue structures[J]. Control and Decision, 2019, 34(7): 1365−1374.

[6] Van P D, Barros A, Bérenguer C, et al. Dynamic grouping maintenance with time limited opportunities[J]. Reliability Engineering & System Safety, 2013, 120: 51− 59.

[7] 徐孙庆, 耿俊豹, 魏曙寰, 等. 考虑相关性的串联系统动态机会成组维修优化[J]. 系统工程与电子技术, 2018, 40(6): 1411−1416. XU Sunqing, GENG Junbao, WEI Shuhuan, et al. Dynamic opportunistic grouping maintenance optimization for series system considering dependencies [J]. Systems Engineering and Electronics, 2018, 40(6): 1411−1416.

[8] 杨元, 黎放, 侯重远, 等. 基于相关性的多部件系统机会成组维修优化[J]. 计算机集成制造系统, 2012, 18(4): 827−832. YANG Yuan, LI Fang, HOU Chongyuan, et al. Opportunistic group maintenance optimization of multi-unit system under dependence[J]. Computer Integrated Manufacturing Systems, 2012, 18(4): 827−832.

[9] 符杨, 杨凡, 刘璐洁, 等. 考虑部件相关性的海上风电机组预防性维护策略[J]. 电网技术, 2019, 43(11): 4057−4063. FU Yang, YANG Fan, LIU Lujie, et al. Preventive maintenance strategy for offshore wind turbines considering component correlation[J]. Power System Technology, 2019, 43(11): 4057−4063.

[10] 葛小凯, 胡剑波, 张博锋. 考虑依赖性的多部件系统状态维修优化仿真建模[J]. 航空学报, 2013, 34(8): 1854−1863. GE Xiaokai, HU Jianbo, ZHANG Bofeng. Simulation modeling for condition based maintenance optimization of multi-component systems with dependencies[J]. Journal of Aeronautics, 2013, 34(8): 1854−1863.

[11] 王红, 杜维鑫, 刘志龙, 等. 联合故障与经济相关性的动车组多部件系统维护[J]. 上海交通大学学报(自然版), 2016, 50(5): 660−667. WANG Hong, DU Weixin, LIU Zhilong, et al. Integrating failure and economic dependence for maintenance of electric multiple unit multi-component system[J]. Journal of Shanghai Jiaotong University (Natural Edition), 2016, 50(5): 660−667.

[12] ZHOU X, XI L, Lee J. Reliability-centered predictive maintenance scheduling for a continuously monitored system subject to degradation[J]. Reliability Engineering & System Safety, 2007, 92(4): 530−534.

[13] SUN Y, MA L, Mathew J. Failure analysis of engineering systems with preventive maintenance and failure interactions[J]. Computers & Industrial Engineering, 2009, 57(2): 539−549.

[14] 兰杰, 袁宏杰, 袁铭, 等. 考虑真实时变环境应力的系统可靠性评估[J]. 北京航空航天大学学报, 2018, 44(2): 406−412. LAN Jie, YUAN Hongjie, YUAN Ming, et al. System reliability assessment under real time-varying environmental stress[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 406−412.

[15] 王灵芝. 以可靠性为中心的高速列车设备维修决策支持系统研究[D]. 北京: 北京交通大学, 2011. WANG Lingzhi. Research on reliability-centered maintenance decision and support system for high-speed train equipments[D]. Beijing: Beijing Jiaotong University, 2011.

[16] 王红, 熊律, 何勇, 等. 考虑故障风险的动车组部件机会维修优化策略[J]. 铁道学报, 2019, 41(3): 79−85. WANG Hong, XIONG Lü, HE Yong, et al. Optimization of opportunistic maintenance for electric multiple unit component considering failure risk[J]. Journal of the China Railway Society, 2019, 41(3): 79−85.

Dynamic group maintenance strategy of EMU system under failure and economic dependence

YANG Guojun1, 2, WANG Hong1, HE Yong1, XIONG Lü1, WANG Hongyu1

(1. School of Mechatronic Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. CRRC Qishuyan Institude Co., Ltd., Changzhou 213011, China)

In order to discuss the group maintenance strategy of EMU complex system under the influence of different traffic demand, based on the theory of fault chain, the process of fault related transmission between components was analyzed. The reliability decline model of components under the influence of failure dependence was established. The demand factor of traffic volume was introduced to describe the dynamic demand of traffic volume. Besides, the component maintenance and adjustment cost model considering the demand of traffic volume was established. Based on the dynamic group method, maintenance activities of components were combined. Dynamic group maintenance model of EMU complex system considering traffic demand was founded. The results show that the reliability evaluation is more scientific considering the fault correlation. The dynamic group method can better adapt to the demand of traffic volume. The economics of EMU system maintenance can be further improved.

system of EMU; failure dependence; economic dependence; dynamic grouping; preventive maintenance

U269.6；TH17

A

1672 − 7029(2021)01 − 0031 − 07

10.19713/j.cnki.43−1423/u.T20200254

2020−03−30

国家自然科学基金资助项目(72061022)；甘肃省自然科学基金资助项目(20JR5RA401)；兰州交通大学青年科学基金资助项目(2019014)

王红(1968−)，男，青海乐都人，教授，从事轨道车辆零部件疲劳可靠性及预防性维护策略；E−mail：wh@mail.lzjtu.cn

(编辑 阳丽霞)