基于预紧力工况下的原位螺栓超声检测研究

王锋，李雄兵

基于预紧力工况下的原位螺栓超声检测研究

王锋1，李雄兵2

(1. 中车长春轨道客车股份有限公司，吉林 长春 130062；2. 中南大学 交通运输工程学院，湖南 长沙 410075)

高铁制动盘螺栓疲劳裂纹可能会危害列车行车安全，有必要进行原位检测。但常用小角度纵波检测未考虑原位状态下预紧力的影响，螺栓缺陷定量精度不足。运用CIVA软件对原位螺栓裂纹进行仿真并优化检测工艺；利用有效弹性常数法表征螺栓在应力诱导下的宏观各向异性，研究预紧力对缺陷定量的影响规律。建立原位状态的螺栓模型，分析折射角，晶片尺寸，频率和带宽对螺栓声场和缺陷回波的影响，选择最佳工艺参数。基于此参数，模拟不同预紧力下不同尺寸缺陷的回波。研究结果表明：不同预紧力下回波幅值不同。最后，绘制缺陷大小−波幅曲线图，实现螺栓缺陷定量分析。对实际螺栓开展原位检测，结果表明考虑预紧力后，缺陷定量误差降低了12%。

螺栓；预紧力；超声原位检测；缺陷定量；CIVA仿真

螺栓作为高铁制动盘的重要紧固件，在列车制动过程中长时间处于高温、高载荷、冲击和振动等恶劣工况下，易于产生疲劳裂纹，存在螺栓断裂等安全隐患[1]。所以，对制动盘螺栓进行疲劳裂纹检测是十分必要的。目前，常用的螺栓无损检测方式为电磁检测和超声检测[2]。由于超声检测具有穿透能力强，灵敏度高，速度快，成本低和对人体无害等诸多优点[3]，且检测时无需将螺栓进行拆解，故其普遍应用于螺栓的裂纹检测。然而，由于螺栓形状的限制，缺陷反射波与干扰波相互作用等因素的影响，已有的螺栓裂纹超声检测方法难免出现漏检、误检。刘洪涛[4]基于多次试验找到了合适频率、折射角的小角度探头，实现了钻铤螺纹根部区域的超声检测，不过没有实现缺陷的定量分析。汪军 等[5]利用CIVA仿真软件，分析频率与晶片尺寸对航空螺栓缺陷判定的影响，但没有考虑未拆卸情况下，螺栓所受到的载荷情况。张海兵等[6]研究了利用瑞利波对螺栓裂纹检测的方法，当折射角变大时瑞利波的检测也变得困难。DONG等[7]利用横波和纵波斜探头对汽轮机紧固螺栓进行超声波检测，基于裂纹波的特征以及螺纹波的位置规律对裂纹缺陷进行判定，该方法仅对螺栓进行了定性判废，未对缺陷大小进行定量分析。综上，虽然螺栓缺陷的超声检测技术已经取得了一些进展，但往往没有考虑原位状态下螺栓受到的预紧力的影响，且没有实现缺陷的定量分析。本文以CRH5和CRH3型系列动车组制动盘盘毂螺栓为研究对象，利用有效弹性常数(effective elastic constants，EECs)模拟螺栓的原位状态，构建螺栓模型，利用CIVA仿真软件，分析频率、晶片尺寸、带宽、折射角对声场强度以及缺陷回波的影响，得到超声检测的最佳工艺参数。通过分析不同大小、位置缺陷的响应，实现缺陷的定量分析。

1 原理

CIVA声场计算的理论基础是Pencil法修正的瑞利积分法[8−9]。瑞利积分的原理是将探头看做离散的点源，介质中任意位置处的声压就是探头中的所有点源在该处产生的声压之和[10]。基于瑞利积分法，介质中任意一点在时刻的声压可以表达为：

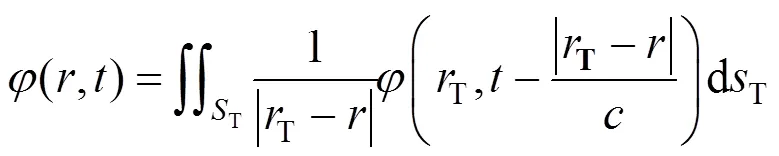
式中：T为探头内发射声场的面积；dT代表探头内的点源的面积；T代表点源的位置；为超声波在介质中的传播速度。由于瑞利积分模型在计算声场传播时，不能实现超声波声压随距离增大而逐渐衰减的计算。因此，需要引入Pencil法对模型进行修正。Pencil法假定超声波传播为一条射线，在传播过程中发生散射。声束在传播过程中的衰减可以用振幅衰减因子表示，并利用Pencil法求解振幅衰减[11]：

式中：为Pencil的截面积；为一个2×2矩阵，与超声波的传播矩阵相关。不同介质中，超声波的传播矩阵不一样，矩阵也不一样。各向同性介质中的矩阵为：

而各向异性介质中的矩阵为：

式中：r表示声束在轴线方向的传播距离；g计算公式为：

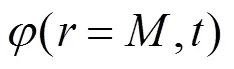
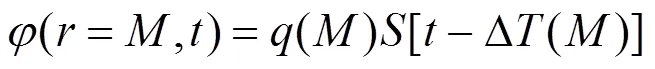
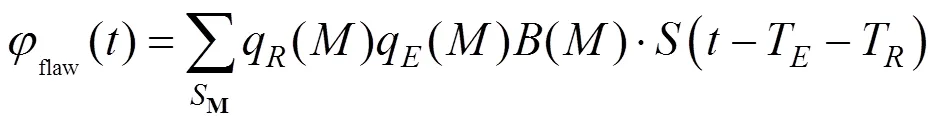
但在CIVA仿真软件中，无法直接添加外载荷，因此已有的CIVA仿真研究都没能对原位状态下螺栓的声场和缺陷响应进行仿真。本文考虑到实际的螺栓超声检测需要在不拆卸的状态下进行，则在螺栓上施加的预紧力不可忽略，因此本文提出了含外载荷的CIVA超声仿真方法。首先，螺栓上需要施加一定的预紧力以保证结构的安全可靠，这使原位状态下的螺栓受到拉伸力的作用，产生轴向应 力[13]；然后，假设无外载荷状态下的螺栓材料为宏观均匀且各向同性的，并假设该材料在受到外载荷后，出现应力导致的宏观各向异性现象；最终，利用CIVA仿真软件的宏观各向异性介质仿真能力，对预紧力作用下螺栓的声场和缺陷响应进行仿真。其中，利用EECs模拟各向同性的螺栓中沿轴向施加载荷后所展现的各向异性特征[14]：

要成功地开展教学，CLIL教师必须：1.具备专业课知识或称学科知识2.具备较强的外语能力3.灵活应用课堂语言4.掌握为学生搭建支架平台的技巧（Instructional scaffolding）。根据Bulter(2005)的一项调查，教师缺乏专业课和英语能力影响课堂CLIL的成功。

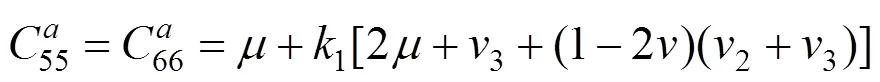
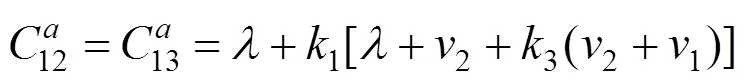
式中：为螺栓孔径；为预紧力。因此，可以借助CIVA软件模拟原位状态下螺栓的声场分布情况以及缺陷响应。

2 预紧力作用下的螺栓检测仿真

本文所采用的是CIVA2020仿真软件中的超声检测模块。利用其声场计算模块对不同参数下螺栓内的声场分布进行对比分析；在缺陷响应模块下，设置不同参数进行超声仿真，模拟真实的缺陷回波信号，选择最佳检测工艺参数。具体步骤如下：

2.1 螺栓模型的建立

如图1所示，为CRH5、CRH3型系列动车组制动盘盘毂所用的M14螺栓，螺栓的材料为30MnB4。设置模型的几何尺寸，对螺栓进行CAD建模并导入CIVA仿真软件中。螺栓的密度为7.8 g/cm3。设置螺栓的预紧力为=55 kN，通过输入有效弹性常数代替弹性常数实现对螺栓原位状态的模拟。螺栓模型的网格精度取决于超声波的波长，通常设网格大小为/5以保证仿真模拟的精度。通过设置计算区域，来形成固定边界以实现波的 反射。

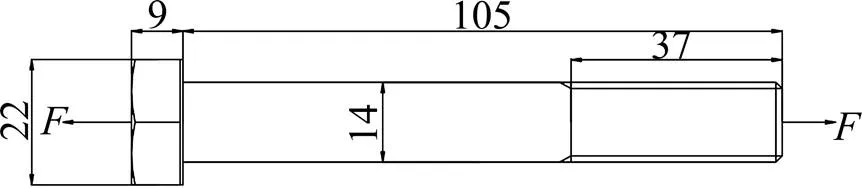
单位：mm

2.2 超声探头的设置

对于螺栓的超声检测，比较常用的探头为：直探头、纵波斜探头和横波斜探头。其中，小角度纵波斜探头的灵敏度最高，且更适用于螺栓端面为平面的情况，故采用纵波斜探头进行检测[5]。设置探头为圆形单晶片，波形为纵波，其入射点为螺栓端面的中心。聚焦方式设置为平面。楔块材料为有机玻璃，其纵波声速为3 080 m/s。设置超声探头的折射角为4°，频率为10 MHz，带宽为50%，晶片尺寸为8 mm。

2.3 声场的仿真

按照以上参数设置，模拟螺栓螺纹处的声场分布情况。如图2所示，图2(a)为CIVA仿真模型，图2(b)为螺栓螺纹处的声场分布图。接着，在保证其他相关参数不变的情况下，再分别设置不同的折射角、中心频率、晶片尺寸和带宽进行超声仿真。可以发现，带宽对声场计算结果几乎没有影响，折射角主要影响主声束的指向。随着晶片尺寸的增加，声场强度的最大值会有所增加，但当晶片尺寸大于工件直径时，声场能量将有所损失，故晶片尺寸的选择应不大于工件尺寸。同时，随着探头中心频率和晶片尺寸的增加，扩散角会更小，声场的聚焦深度会增大，需要根据缺陷的深度选择不同的探头频率以及晶片尺寸。为了选择最合适的工艺参数，还需要分析不同参数对缺陷响应的影响。

2.4 缺陷波的仿真

根据经验，当制动盘盘毂的螺栓和螺母拧紧后，受力最大的区域是螺母与螺杆接触的第一个螺牙处，疲劳裂纹有很高的频率会产生在这一位 置[15]。采用凹槽模拟实际工程中的螺栓裂纹缺陷，设置凹槽缺陷深度为1 mm，沿螺栓径向切割。缺陷中心与螺帽端部的垂直距离为93.2 mm。按照以上参数设置，模拟螺栓的缺陷响应。曲线回波信号如图2(c)所示。

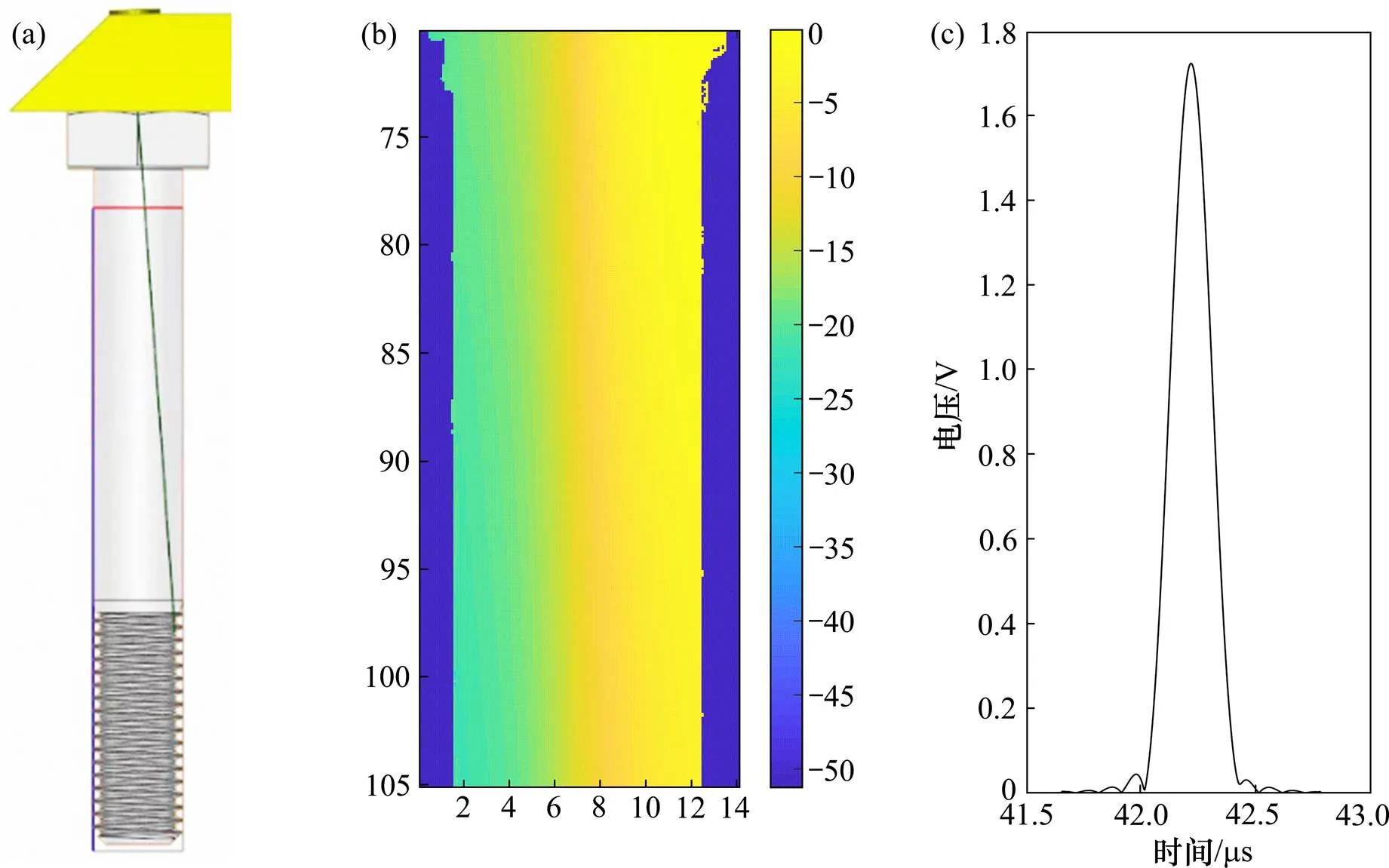
(a) CIVA仿真模型；(b) 声场分布图；(c) 缺陷回波信号

3 基于CIVA的螺栓检测工艺优化

超声纵波斜探头的检测工艺需要确定一系列的参数，如中心频率、折射角、晶片尺寸和带宽等。通过设置不同的探头频率、晶片尺寸、带宽以及折射角对螺栓进行仿真模拟，分析不同参数对声场强度和缺陷响应的影响。选择最佳工艺参数，指导螺栓超声无损检测的工艺制定。

3.1 折射角的影响

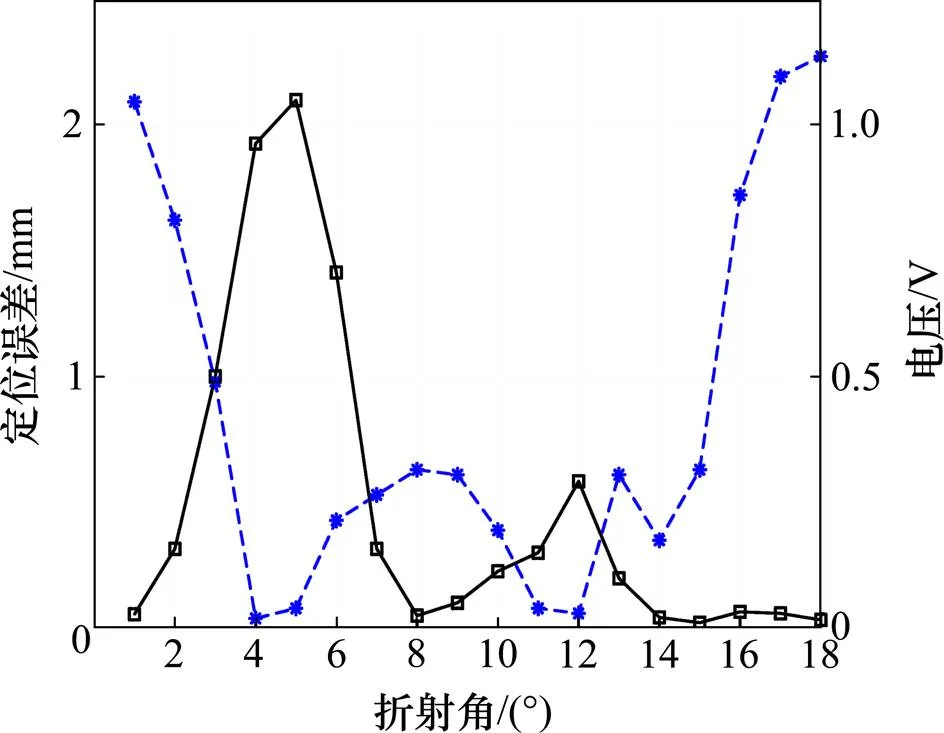
图3 折射角对距离误差及回波波幅的影响

图4 中心频率对距离误差及回波波幅的影响

3.2 中心频率的影响

按照先前的设置，设折射角为4°，为研究探头中心频率对螺栓裂纹缺陷检测的影响，设置频率为2～14 MHz，计算获得的缺陷回波。由图4可以看出，对于螺栓侧面的裂纹缺陷，仿真所检测到的缺陷中心位置随频率变化的波动并不大，保持在0.1 mm以内，与折射角相比，影响较小。但频率对缺陷反射波的波幅影响较大。当频率为10 MHz时，反射波波幅最大，更容易区分缺陷波，发现细小缺陷。所以选择10 MHz时的检测效果最好。

3.3 晶片尺寸的影响

保持其他参数不变，为研究晶片尺寸对螺栓裂纹缺陷检测的影响，设置晶片尺寸为2～14 mm，计算获得的缺陷回波。图5结果显示，设置不同晶片尺寸下所测出的缺陷回波有所不同，但仿真检测到的缺陷中心位置随晶片尺寸的变化并不大，相差保持在0.05 mm以内。不同晶片尺寸对波幅也有一定的影响，晶片尺寸过小会造成波幅降低，不易于观察缺陷波。结合缺陷定位和回波波幅分析可知，对于螺纹的疲劳缺陷，当晶片尺寸为8 mm时，检测效果更好。

图5 晶片尺寸对距离误差及回波波幅的影响

3.4 带宽的影响

保持其他参数不变，为研究带宽对螺栓侧面缺陷检测的影响，设置带宽为20%～80%，计算获得的缺陷回波。由图6可以看出，不同带宽的探头均可检测出缺陷。带宽对缺陷的定位精度以及缺陷回波的波幅影响都不大，但对缺陷回波的波形影响很大。当带宽过小时，缺陷回波信号易与侧壁回波混合，不利于区分缺陷波。缺陷回波和声场强度受带宽改变的波动均较小，一般情况下，选择带宽为50%左右即可。

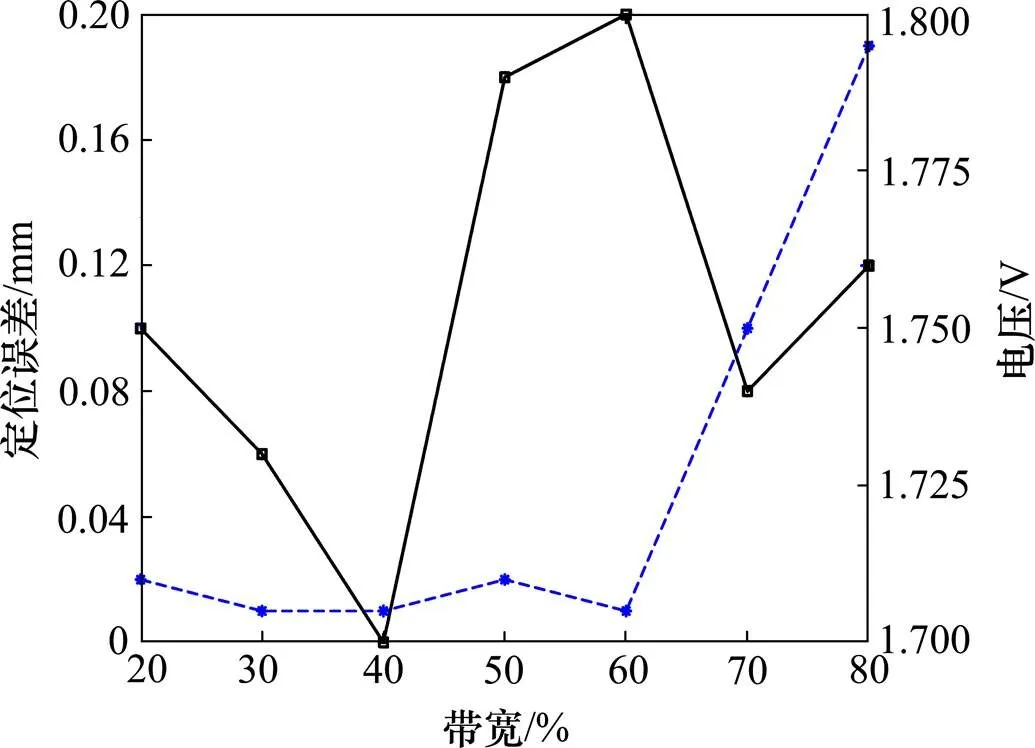
图6 带宽对距离误差及回波波幅的影响

4 螺栓的缺陷定量方法

按照仿真得到的最佳工艺参数，设中心频率为10 MHz，折射角为4°，带宽为50%，晶片尺寸为8 mm。设缺陷为切口深度1 mm的凹槽缺陷，疲劳缺陷通常只出现螺杆与螺母连接的螺牙处，即在距螺帽93～93.4 mm以及95～95.4 mm螺牙处，对这段距离上的缺陷回波最高点进行标记，并记录在表1中。从表1可知，由于检测区域较小，且检测区域距离螺帽端面较远，缺陷回波波幅随距离变化的幅度并不大。

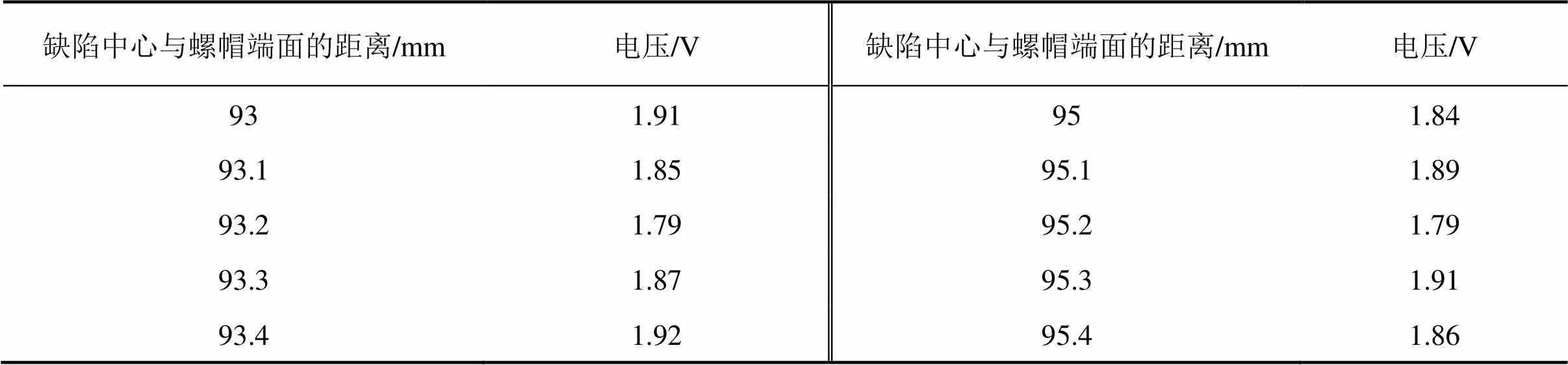
表1 不同位置处1 mm凹槽缺陷的回波幅值

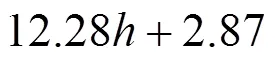
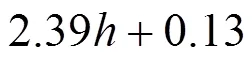
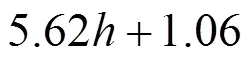
也可以得到由缺陷回波波幅求解凹槽切口深度的表达式为：

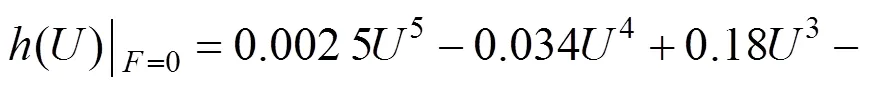
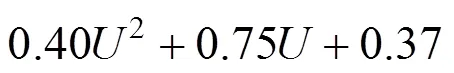
将检测到的缺陷回波波幅代入式(11)便可以求出缺陷切口深度，实现缺陷大小的准确判定。此外，从图7可以看出，随着缺陷切口深度的不断增加，缺陷回波的波幅也不断增大。且不同预紧力下的回波波幅是不一样的，但曲线的变化形式大致是一样的。无应力的曲线与另2条曲线均有交点，相交之前同样深度缺陷无应力状态下的缺陷回波更小，相交之后则无应力状态下的缺陷回波更大。可知，若不考虑螺栓原位状态下载荷的作用，测出的缺陷大小与真实缺陷会存在一定的误差。图8展示了不同预紧力下1 mm缺陷的回波。可以发现，预紧力影响了缺陷回波的幅值和缺陷定位。倘若不考虑螺栓原位状态下预紧力的影响，测得的缺陷尺寸将偏大，可能会出现错判、误判的情况，无法保证检测的可靠性。所以对原位状态螺栓进行缺陷定量分析时不能忽略预紧力的影响。

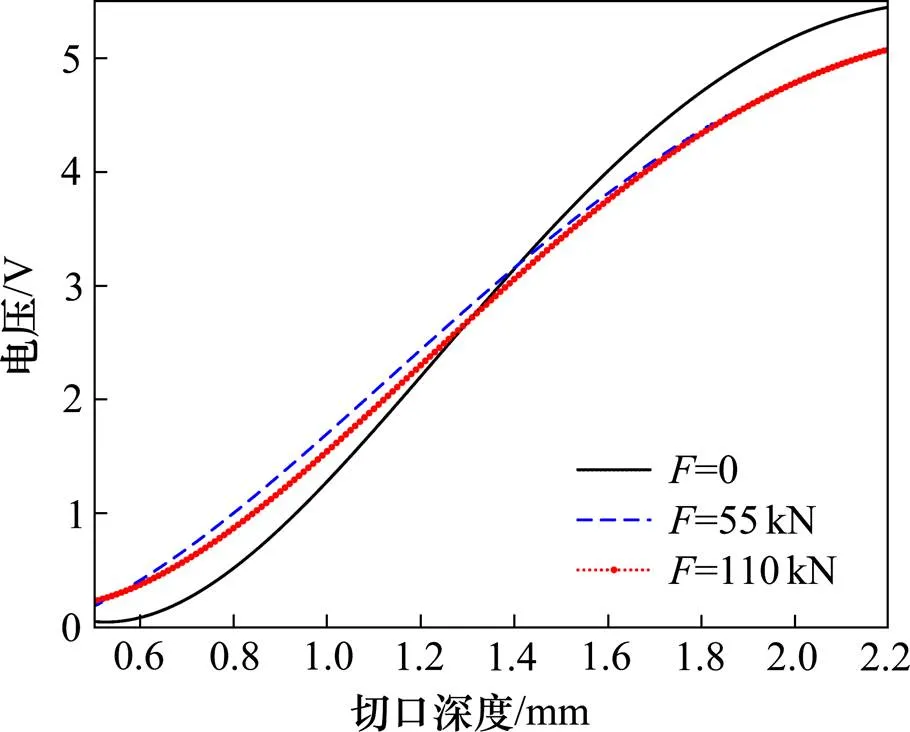
图7 不同预紧力下切口深度对回波波幅的影响

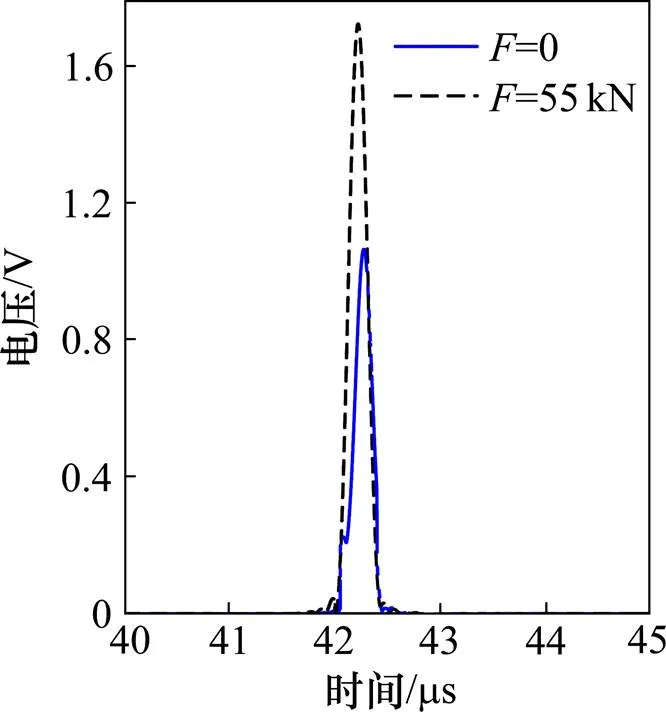
图8 不同预紧力下的缺陷回波

5 实验验证

按照以上工艺参数，利用Krautkramer USM 36数字超声波探伤仪对螺栓进行超声检测。在距螺帽端部93 mm处的螺牙上加工一个1 mm的人工缺陷。如图9所示，首先在无应力的状态下对螺栓缺陷进行超声检测。将探头晶片装在内径与螺帽尺寸相当的壳体内，检测时将装好的探头在螺帽一端旋转一周，实现超声扫查。缺陷波的超声检测结果如图11所示，可以明显发现缺陷波的存在，且与图8中CIVA仿真所生成的超声A波包络线大致相符。多次重复该实验，将得到的电压幅值代入式(13)可以得到的缺陷尺寸为0.94±0.10 mm。

随后，将带有人工缺陷的螺栓与制动盘装配到一起，并施加预紧力为55 kN。如图10所示，按照同样的步骤对原位状态下的螺栓缺陷进行检测，一次超声检测结果如图11所示。多次重复该实验，将得到的电压幅值分别代入式(13)和式(14)可以得到的缺陷尺寸分别为1.16±0.14 mm以及1.04±0.08 mm。实验检测结果可知，倘若不考虑原位状态下应力的影响，检测到的缺陷尺寸与真实尺寸不符，结果较真实尺寸偏大。这与CIVA仿真所得到的结论一致。考虑预紧力后，定位误差降低了约12%。

图9 无应力螺栓的检测示意图

图10 原位螺栓的检测示意图

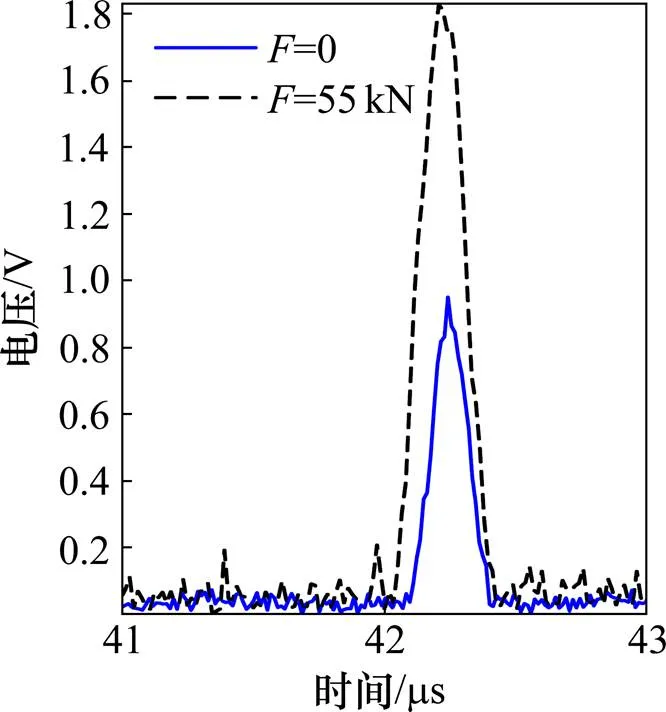
图11 超声探伤仪检测结果

6 结论

1) 基于CIVA仿真软件对螺栓超声检测工艺进行研究，结果显示预紧力为55 kN时，在折射角4°，中心频率10 MHz，晶片尺寸8 mm和带宽50%的工艺参数下检测效果较好；计算电压幅值−缺陷大小关系式，实现螺栓裂纹缺陷的定量分析。仿真结果可以指导螺栓检测工艺的制定。

2) 不同预紧力下缺陷回波波幅不一样，但均会随着缺陷切口深度的增加而不断增大。螺栓裂纹缺陷的定量分析不可忽略预紧力的作用。实际螺栓的超声检测证明，考虑预紧力作用后，定位误差降低了约12 %。

[1] 范童柏, 任尊松, 王文静, 等. 动车组制动盘螺栓载荷测试及疲劳损伤研究[J]. 机械工程学报, 2019, 55(14): 80−87. FAN Tongbai, REN Zunsong, WANG Wenjing, et al. Study on bolt load test and fatigue damage of brake discs of EMU[J]. Journal of Mechanical Engineering, 2019, 55(14): 80−87.

[2] 陈国达, 郗枫飞, 计时鸣, 等. 螺栓无损检测方法综述[J]. 制造技术与机床, 2017(11): 22−28. CHEN Guoda, XI Fengfei, JI Shiming, et al. Review of nondestructive testing methods for bolts[J]. Manufacturing Technology & Machine Tool, 2017(11): 22−28.

[3] 戴万林, 杨岳, 刘希玲, 等. 钢轨轨头内缺陷的超声相控阵DAC定量方法[J]. 铁道科学与工程学报, 2018, 15(1): 188−195. DAI Wanlin, YANG Yue, LIU Xiling, et al. DAC quantitative method of ultrasonic phased array for rail head defects[J]. Journal of Railway Science and Engineering, 2018, 15(1): 188−195.

[4] 刘洪涛. 钻铤螺纹小角度探头检测方法研究与应用[J]. 无损检测, 2020, 42(5): 79−80. LIU Hongtao. Research and application of detection method of small angle probe for drill collar thread[J]. Nondestructive Testing, 2020, 42(5): 79−80.

[5] 汪军, 钱嘉锟, 车天泽. 核电站汽轮机高压缸内缸螺栓超声检测[J]. 无损检测, 2013, 35(5): 72−74. WANG Jun, QIAN Jiakun, CHE Tianze. Ultrasonic testing for the bolt of the high pressure inner cylinder of turbine in the nuclear power plant[J]. Nondestructive Testing, 2013, 35(5): 72−74.

[6] 张海兵, 温德宏. 基于CIVA的航空螺栓仿真检测试验研究[J]. 无损探伤, 2020, 44(4): 41−43. ZHANG Haibing, WEN Dehong. Research on simulation test of aircraft bolts based on CIVA[J]. Nondestructive Testing Technology, 2020, 44(4): 41−43.

[7] DONG M S, Whan W K. A new ultrasonic technique for detection and sizing of small cracks in studs and bolts[J]. Journal of Nondestructive Evaluation, 1995, 14(4): 201− 206.

[8] 吴冲, 王子成. 超声检测模拟仿真软件应用与发展现状[J]. 工具技术, 2018, 52(11): 22−25. WU Chong, WANG Zicheng. Application and development status of simulation software for ultrasonic testing[J]. Tool Engineering, 2018, 52(11): 22−25.

[9] Calmon P, Mahaut S, Chatillon S, et al. CIVA: An expertise platform for simulation and processing NDT data[J]. Ultrasonics, 2006, 44(8): 975−979.

[10] Veerman J A C, Rusch J J, Urbach H P. Calculation of the rayleigh-sommerfeld diffraction integral by exact integration of the fast oscillating factor[J]. Journal of the Optical Society of America A Optics Imageence & Vision, 2005, 22(4): 36−46.

[11] Gengembre N. Pencil method in elastodynamics: Application to ultrasonic field computation[J]. Ultrasonics, 2000, 38(18): 495−499.

[12] Lhemery A. A model for the transient ultrasonic field radiated by an arbitrary loading in a solid[J]. Insight NDT, 2007, 49(2): 93−97.

[13] 周春华. 螺栓预紧精度及预紧可靠性分析[J]. 铁道科学与工程学报, 1996, 14(3): 58−63. ZHOU Chunhua. Precision and reliability of preloading of bolted joints[J]. Journal of Railway Science and Engineering, 1996, 14(3): 58−63.

[14] Quiroga J E, Mujica L, Villamizar R, et al. Estimation of dispersion curves by combining Effective Elastic Constants and SAFE Method: A case study in a plate under stress[J]. Journal of Physics: Conference Series, 2017(842): 012069.

[15] 陈士华, 刘仕远, 圣兆兴, 等. M14轴盘螺栓在线超声探伤[J]. 轨道交通装备与技术, 2019(5): 62−64. CHEN Shihua, LIU Shiyuan, SHENG Zhaoxing, et al. Ultrasonic testing of on-line M14 axle disc bolt[J]. Rail Transportation Equipment and Technology, 2019(5): 62− 64.

Study of ultrasonic testing method for in-situ bolts based on pre-tightening force

WANG Feng1, LI Xiongbing2

(1. CRRC Changchun Railway Vehicles Co., Ltd., Changchun 130062, China;2. School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)

Bolts fatigue crack of EMU brake disc may endanger the train safety, so the in-situ testing is necessary. However, the widely used small-angle longitudinal wave detection method cannot consider the influence of pre-tightening force of in-situ bolts, as a result it can’t ensure the sizing accuracy of bolts crack. In this paper, simulation studies were carried out for in-situ bolts fatigue crack by CIVA simulation software to optimize the process parameters. The effective elastic constants method was used to characterize the stress-induced macroscopic anisotropy of bolts, and then the influences of pre-tightening force on flaw sizing were studied. By establishing the simulation model of in-situ bolts, the influences of refraction angle, chip size, frequency and bandwidth on ultrasonic field and defects in response were analyzed, and the optimum process parameters were selected. Based on the optimum parameters, defects wave with different depths under different pre-tightening forces were simulated. The simulation results show that the amplitudes of defects wave under different pre-tightening forces are different. Finally, flaw sizing analysis of bolts can be realized by making defect size-amplitude curve. In-situ ultrasonic testing for fastening bolts of EMU brake disc was carried out, and the experimental results show that flaw sizing error is reduced by 12% after considering the influence of pre- tightening force.

bolts; pre-tightening force; in-situ ultrasonic testing; flaw sizing; CIVA simulation

TB255

A

1672 − 7029(2021)01 − 0038 − 08

10.19713/j.cnki.43−1423/u.T20200833

2020−09−01

国家重点研发计划资助项目(2017YFB1201302-13)

李雄兵(1977−)，男，湖南邵东人，教授，博士，从事超声无损检测与评价研究；E−mail：lixb213@csu.edu.cn

(编辑 蒋学东)