轴承球变曲率研磨盘沟槽结构参数数值优化研究*

李晓琪，柯明峰，祝佳俊，周芬芬，吕冰海*

(1.浙江工业大学 机械工程学院，浙江 杭州 310000；2.台州学院 机械工程学院，浙江 台州 318000)

0 引 言

精密轴承球是滚动轴承中最关键的元件。精密球体的形状精度、表面质量和一致性对轴承运动精度和使用寿命有至关重要的影响。

精密轴承球的加工是在球体和研磨盘之间添加磨粒，由驱动盘以摩擦力的形式提供驱动力带动球体，并且球体与研磨盘研磨面的接触点不断更换，通过磨粒对球面材料以滑刻或犁削的形式进行去除。

目前，国内外精密轴承球的加工方式按磨盘驱动个数及加工中有无磁性液体等特性主要分为单转盘驱动加工方式、多转盘驱动加工方式和磁流体加工方式。1976年，INAGAK等[1]首次提出了同心圆V形沟槽加工方式；ZHANG等[2]基于运动学原理，分析了球体在单个同心圆沟槽滚道中运动产生的球面轨迹的分布特点；黑部利次等[3]提出了三转盘驱动加工方式，使研磨轨迹能均匀覆盖球面；袁巨龙等[4]在此基础上提出了有双自转球体研磨方式，及双转盘偏心同心圆V形槽加工方式[5]等系列加工方式；TANI Y和KAWATA K[6]提出了磁流体研磨方式(magnetic fluid polishing,MFP)；ZHANG等[7]将其进一步改进，提出了偏心式磁流体加工方式。

近年来，为了进一步提高精密轴承球的加工效率，浙江工业大学袁巨龙等[8]提出了变曲率沟槽研磨方法，该加工方法可对精密球体进行循环批量加工，并能实现球体的高效高一致性加工[9]。

为优化变曲率沟槽结构参数，本文提出一种数值分析方法，通过数值仿真分析变曲率沟槽几何参数对球面加工轨迹形态、球面加工轨迹点分布均匀性的影响规律，并结合正交试验设计和方差分析法，分析变曲率沟槽几何参数对球面加工轨迹均匀性的影响权重，以获得最佳几何参数组。

1 变曲率沟槽加工方式基本原理

变曲率沟槽球体加工方式的基本原理如图1所示。

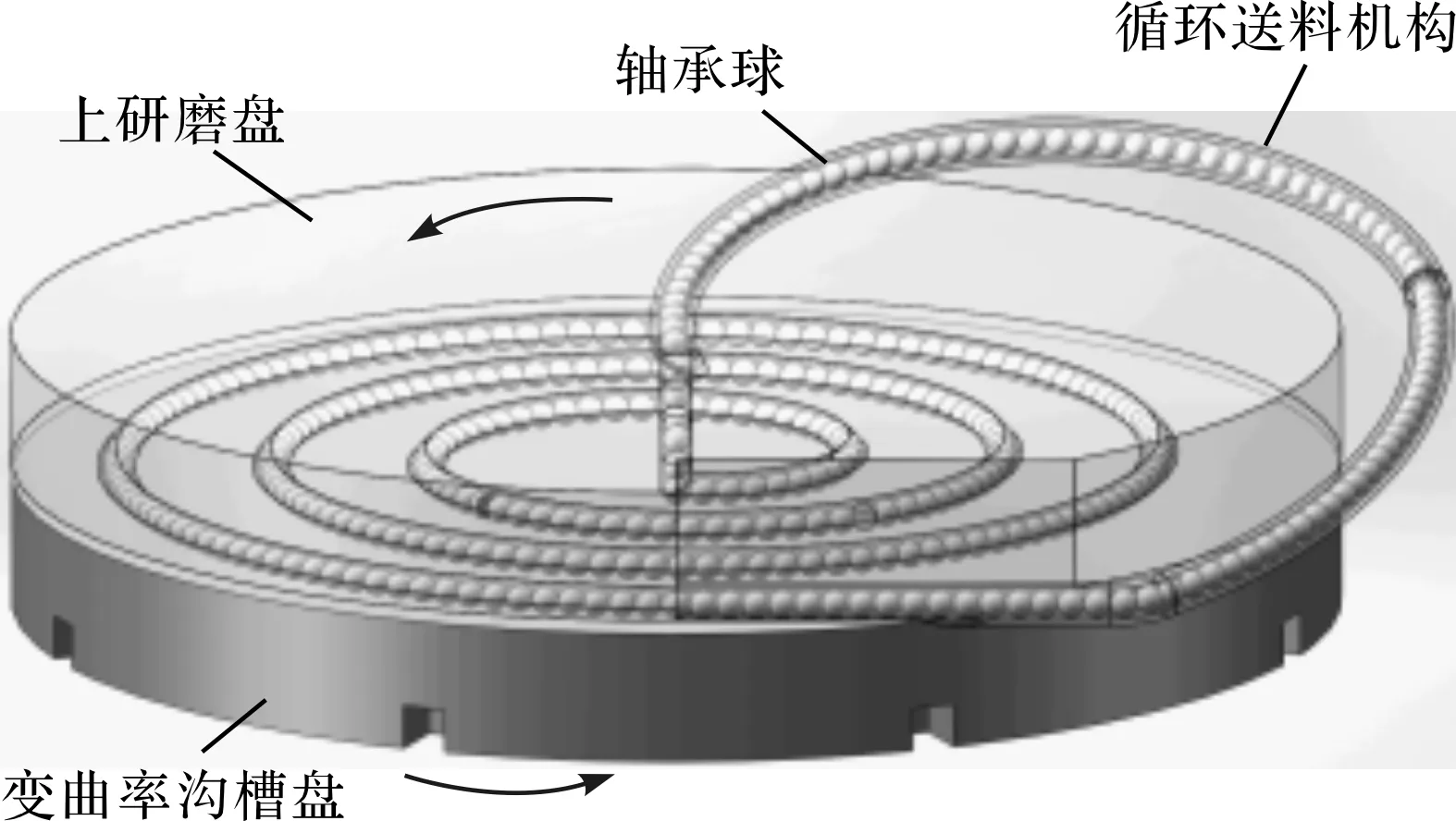
图1 变曲率沟槽球体加工方式的基本原理

该加工方式的基本原理为：

将变曲率沟槽盘代替传统同心圆沟槽盘，利用球体在变曲率沟槽中接触点位置及相对速度的变化，使球体由磨盘中心向外作自旋角连续变化的运动，从磨盘入料口经过整个变曲率沟槽路径至磨盘出料口完成单个周期加工，之后借助循环送料机构再次进入磨盘加工区域实现循环加工，实现了加工轨迹均匀包络球面效果，从而获得高精度、高一致性轴承球。

该加工方法既有与V形槽研磨方式相当的装球量，又具有双自转研磨方式的加工精度一致性，结构简单，便于工程实现。

变曲率沟槽球体加工方式沟槽几何关系如图2所示。

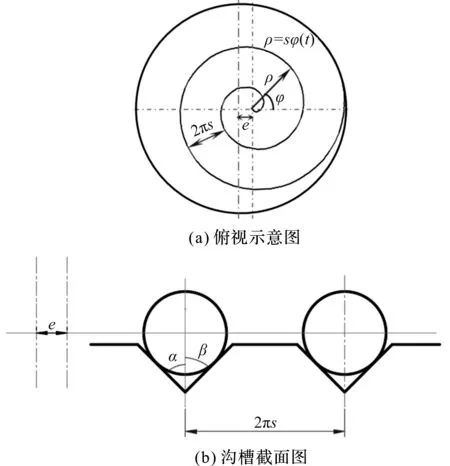
图2 变曲率沟槽球体加工方式沟槽几何关系

加工沟槽按阿基米德螺旋线排布，其极坐标表达式为：

ρ=sφ(t)

(1)

式中：ρ—极径，mm；φ(t)—随时间变化的极角，°；s—沟槽间距系数，mm。

选取单颗球体进行几何运动学分析[10]，可得双转盘沟槽偏心式变曲率沟槽加工系统总的几何运动学方程组如下：

(2)

式中：rb—球体半径，mm；ωg，ωb—自转角速度的两个分量，r·min-1；γ，θ—方位角，rad；α，β—沟槽半角，°；lA，lB，lC—盘上接触点到主轴中心的距离，mm；e—沟槽中心与磨盘主轴中心的偏心距，mm；τA，τB，τC—接触点盘上线速度与τ轴夹角，°。

由式(2)可见，表征球体运动规律的自转角速度和自转角ωg、ωb、θ和γ与V形槽半角、磨盘转速、变曲率沟槽滚道极径和偏心距等因素均有关。

为避免不同球径影响模型的适应性，偏心距和沟槽滚道极径均取其与球体半径rb的比值，即分别表达为ρ/rb和e/rb。

2 球面加工轨迹均匀性的定量评价方法

球面材料去除发生在球-盘接触点位置处，球面加工轨迹分布越均匀，则球面材料去除机率越均匀。

本文采用球面的等面积网格划分方法[11]，即把球面按地球经纬方向划分成许多相等的单元，统计每个网格区域内的轨迹点数量；采用统计方法计算各区域内研磨轨迹密度的标准差SD值，将其作为球面研磨轨迹均匀性的定量评价值(SD越小，轨迹点分布均匀性越好)[12]；以研磨轨迹均匀性为目标，采用寻优方法，获得最佳几何参数组。

仿真分析流程图如图3所示。

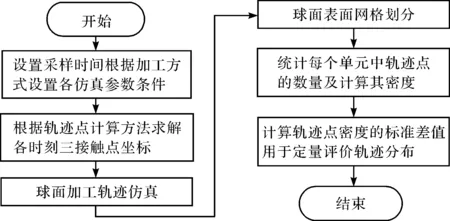
图3 仿真分析流程图

仿真条件如表1所示。

表1 仿真条件

变曲率沟槽球体加工方式下球面加工轨迹分布形态仿真图如图4所示。

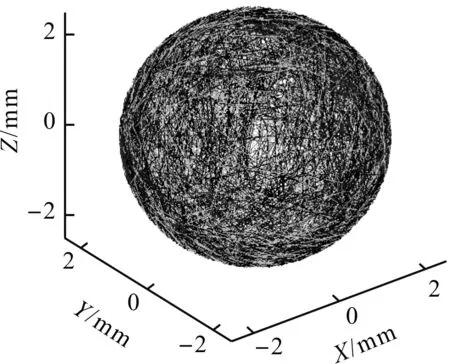
图4 球面加工轨迹分布形态仿真图

单个加工周期后，球体加工轨迹能够均匀包络整个球面。

3 变曲率沟槽几何参数的影响

(1)偏心距的影响。

偏心距对加工轨迹均匀性标准差值SD的影响如图5所示。

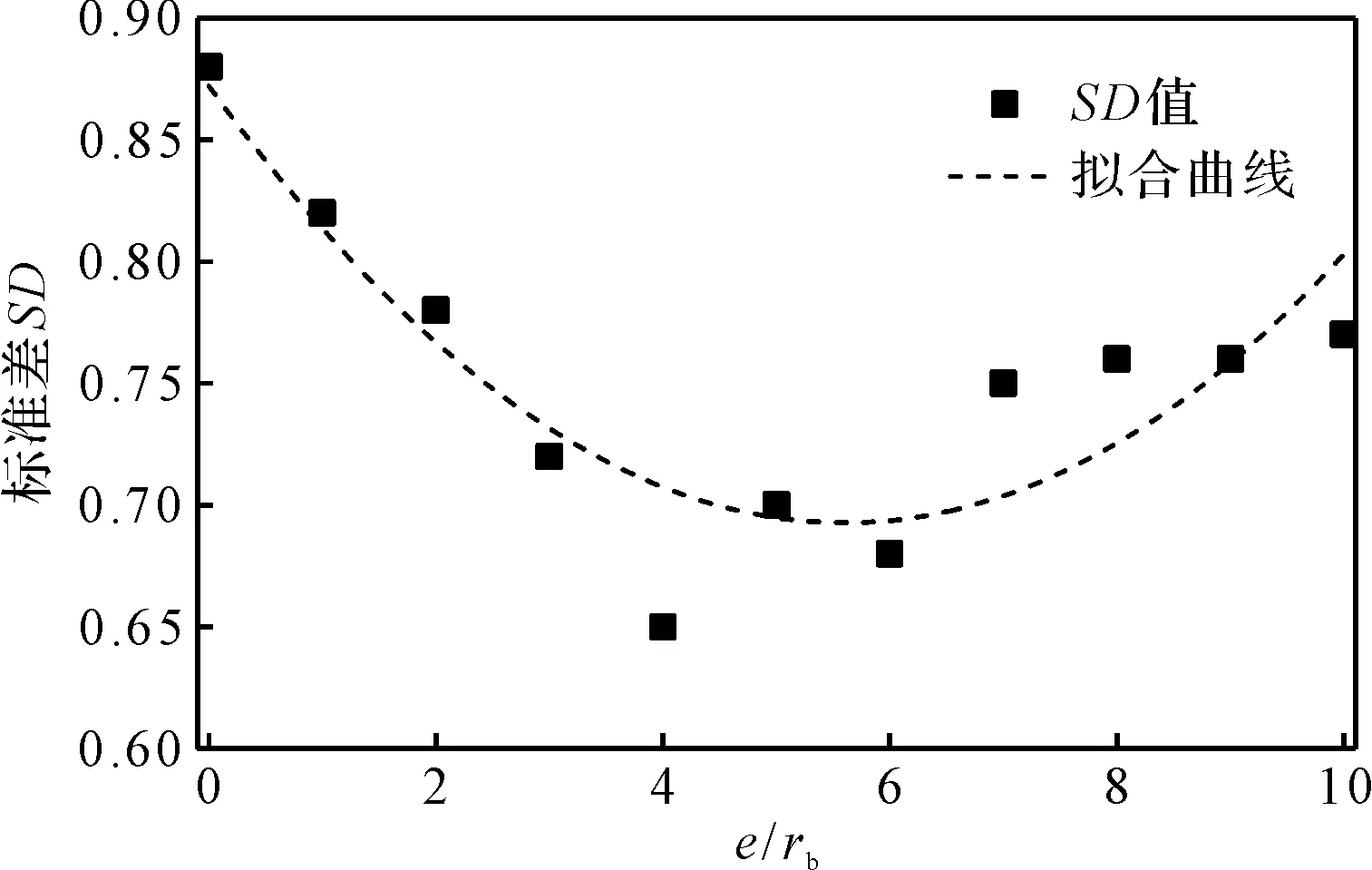
图5 偏心距对加工轨迹均匀性标准差值SD的影响

拟合曲线反映了SD的变化趋势，SD值随着偏心距的增加逐渐减小，当e/rb=4时，SD达到最小值，之后再增加偏心距，SD值逐渐增加，此时由于自转角和自转角速度的变化幅值均增大，自转角和自转角速度的综合作用使得轨迹形态分布呈现多方向性，轨迹点分布更加密集，能够全包络整个球面。

(2)沟槽半角的影响。

沟槽半角对加工轨迹均匀性标准差值SD的影响如图6所示。

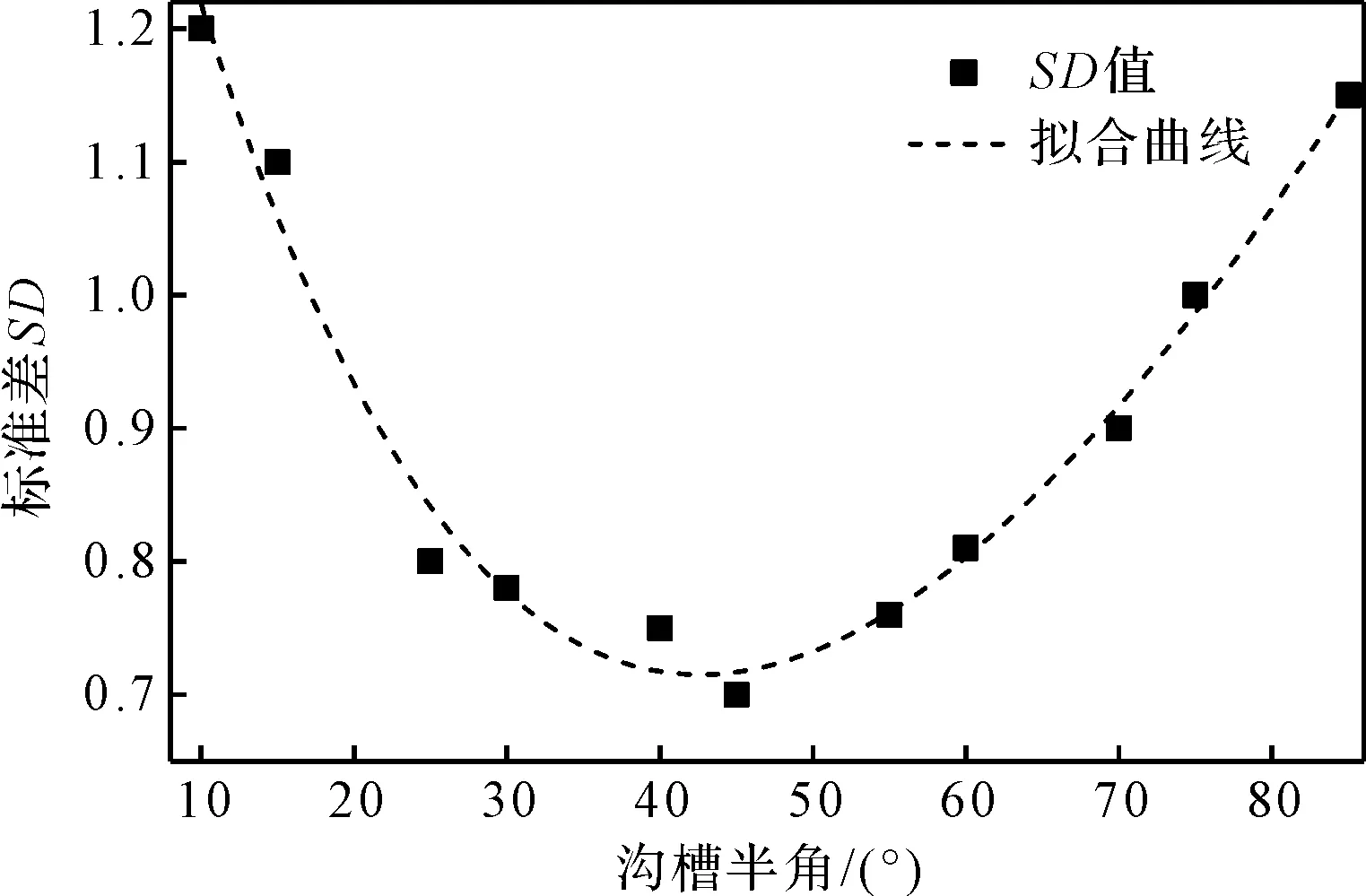
图6 沟槽半角对加工轨迹均匀性标准差SD的影响

随着沟槽半角的增加，SD值呈现抛物线变化状态，先递减后增加，在沟槽半角为45°时，SD值最小。这是由于随着沟槽半角α的增加，自转角速度Z轴上的正交分量相位增加，但是相位的增加并不会影响加工轨迹的分布形态，其影响的是轨迹分布的位置。

(3)沟槽滚道极径的影响。

沟槽滚道极径对加工轨迹均匀性标准差SD的影响如图7所示。

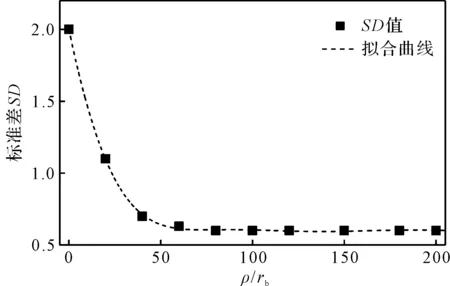
图7 沟槽滚道极径对加工轨迹均匀性标准差SD的影响

随着沟槽滚道极径的增加，SD值快速下降，ρ/rb>50后，SD值仍逐渐减小，但减小速率非常缓慢，因此可视为当ρ/rb不断增大后，SD值逐渐趋于稳定。

(4)沟槽间距的影响。

沟槽间距对加工轨迹均匀性标准差值SD的影响如图8所示。

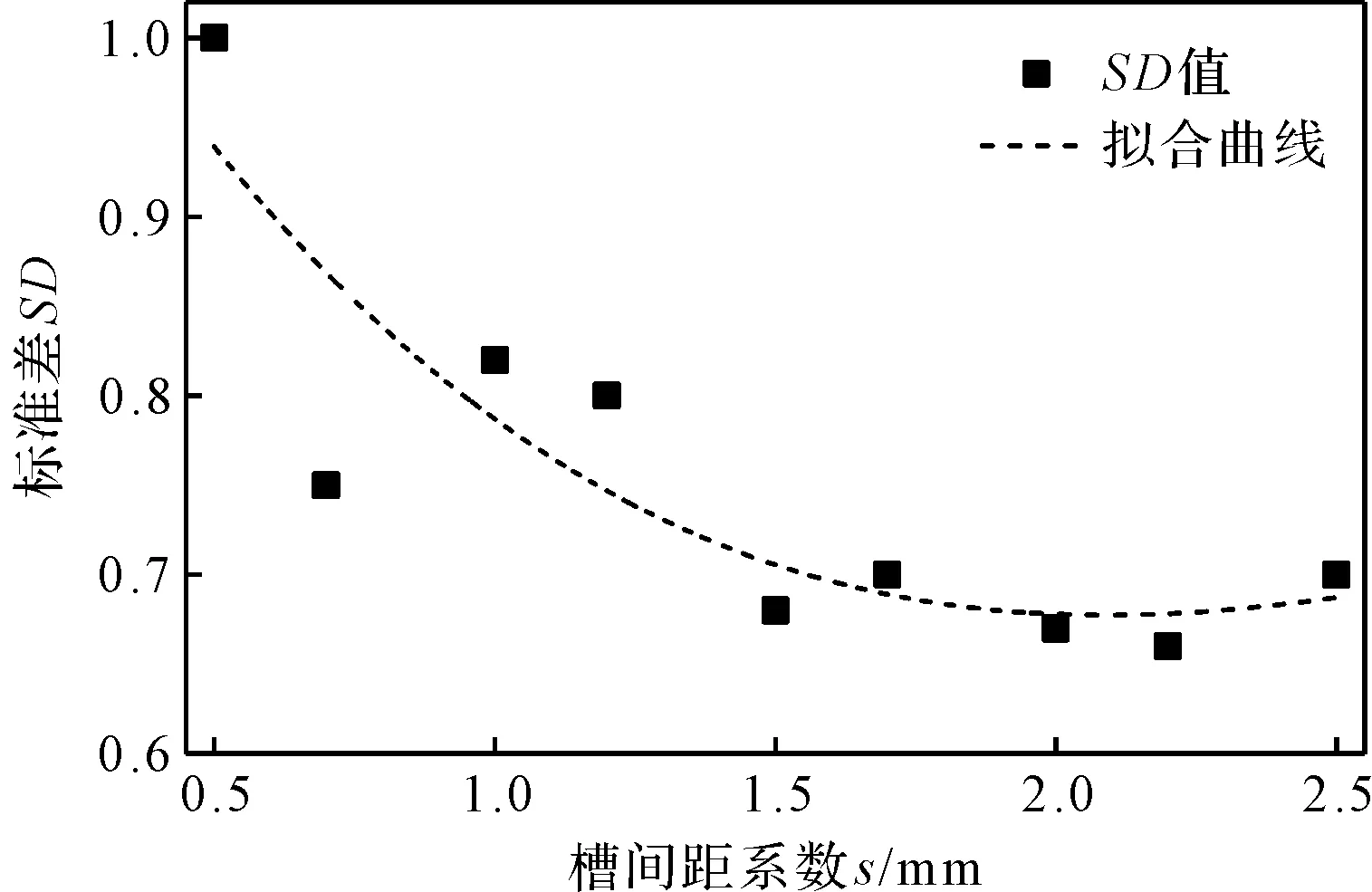
图8 沟槽间距对加工轨迹均匀性标准差值SD的影响

随着s值增大，SD值逐渐减小，当s>2后，SD值减小的速率变缓慢。对于变曲率沟槽加工方式，相邻两槽之间的距离为定值2πs，s越大，ρ的增长速率越快，使得球体自转角速度的变化增大，同时结合沟槽滚道越长越利于球面轨迹的分布，可得s增大，加工轨迹分布均匀性越好。但是考虑到加工效率，在相同的盘径下，过大的s值，将使沟槽滚道长度减小，装球量减小。

4 正交试验和方差分析

为了分析沟槽内角α、沟槽外角β、偏心距e/rb及槽间距系数s对球面加工轨迹均匀性的影响程度，设计了一组正交仿真实验，以标准差SD作为试验指标。

正交仿真试验因素水平如表2所示。

表2 正交仿真试验因素水平表

为了可对4因素4水平进行正交试验和方差分析，本文选取5因素4水平的正交试验设计表L16(45)[13]，第5列E作空列处理为未知因素。

正交试验方案及试验结果如表3所示。

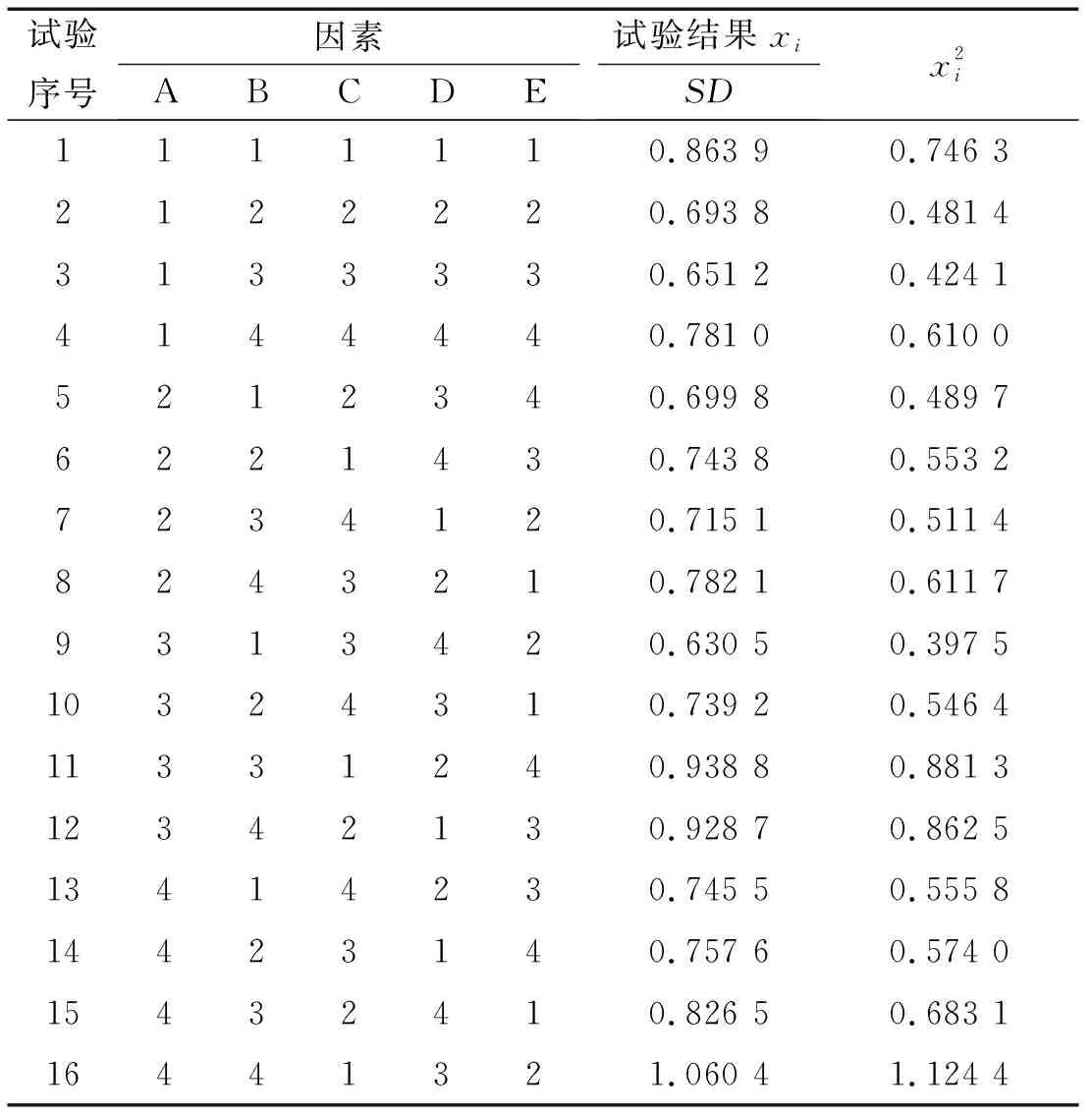
表3 正交试验方案及试验结果

试验指标SD的数据处理如表4所示。

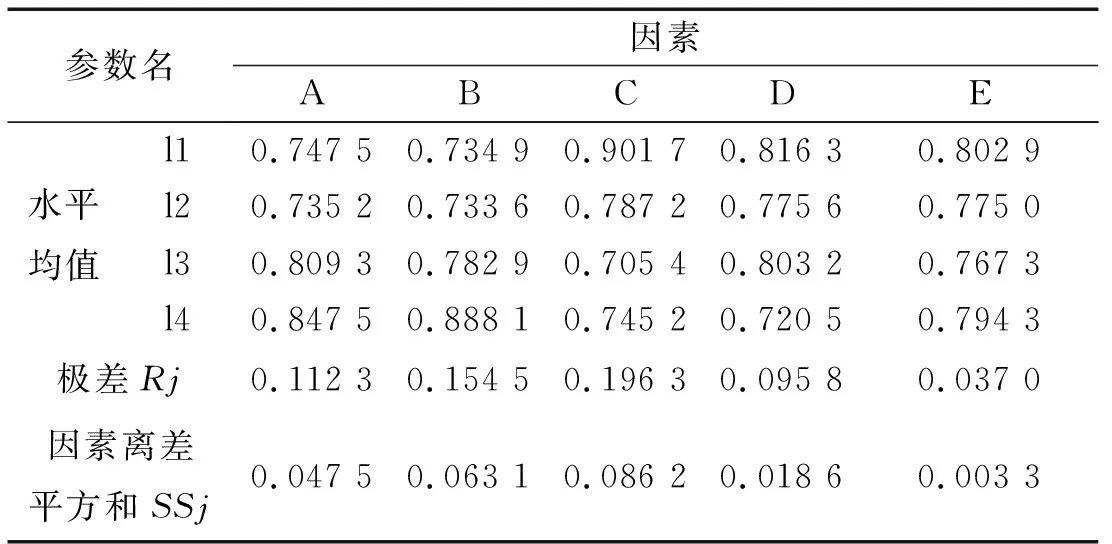
表4 试验指标SD的数据处理表

根据分析各个参数的水平均值响应的最低值，得出最佳几何参数组合：偏心距e/rb=4，沟槽半角α=β=45°，沟槽滚道极径ρ/rb=60，沟槽间距系数s=2，与单因素分析结果基本一致。

根据ANOVA中影响权重SA为SSj值占总校平方和的百分比[14]计算可得，变曲率沟槽几何参数对标准差SD的影响权重如图9所示。

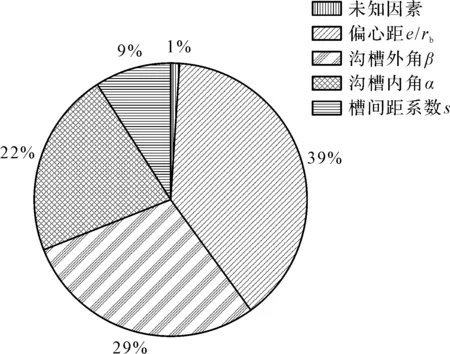
图9 变曲率沟槽几何参数对标准差SD的影响权重

偏心距e/rb的影响权重为39%，沟槽外角β为29%，沟槽内角α为22%，槽间距系数s为9%。这与前面的单因素分析相吻合，偏心距的有无很大程度上影响球面加工轨迹的分布。

5 验证实验与结果分析

基于上述理论分析成果，为验证上述仿真对轴承球研磨变曲率沟槽结构参数优化结果的正确性，本研究搭建了变曲率沟槽球体加工实验装置。实验选用公称直径8.731 mm的轴承钢球为加工对象，原始精度约为G10级。

实验参数如表5所示。

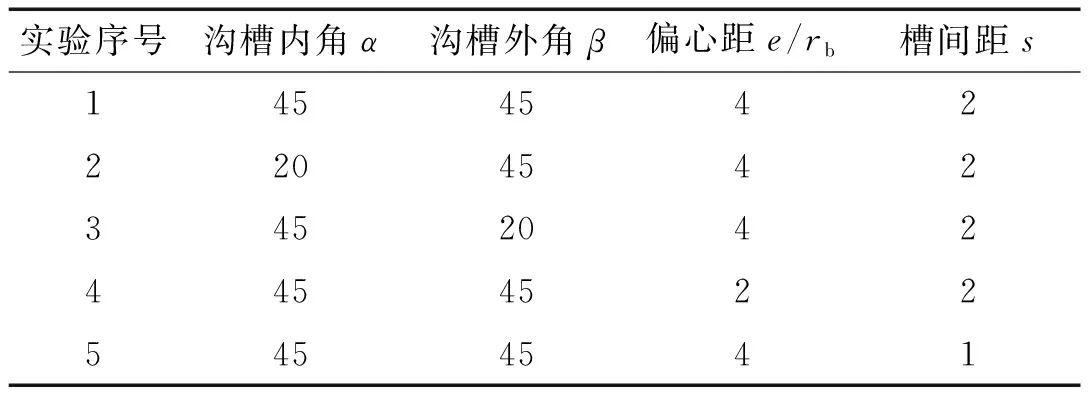
表5 实验参数表

表5中：实验1为最优工艺参数组合下的实验组，为了比较各参数的影响程度，其他每组实验根据仿真结果，只改变其中一个加工参数，其他参数保持不变；实验2只改变沟槽内角，取α=20°；实验3只改变沟槽外角，取β=20°；实验4只改变偏心距大小，取e/rb=2；实验4只改变槽间距系数，取s=1。

加工条件如表6所示。

表6 加工条件

以钢球批平均球度作为变曲率沟槽球体加工实验轨迹均匀性的指标，评价变曲率沟槽工艺参数对均匀性的影响。

本研究采用三丰(Mitutoyo)的RA-1500型圆度仪，对每粒球体3个相互垂直方位的圆度进行检测，取最大值作为该球的球度误差。

每次实验后随机抽测5颗球测量，取平均值，实验结果如图10所示。

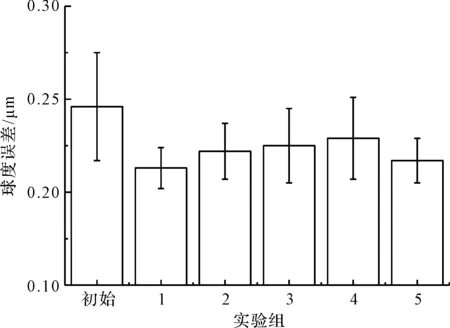
图10 实验结果

由图10可知：加工4 h后，球度误差在最优仿真工艺参数下，能够达到最小值，从0.057 μm降低至0.022 μm；其他实验参数下，平均球度误差值由小到大的实验组依次为：实验5<实验2<实验3<实验4，其球度误差值也均有所减小。

由此可见：实验结果与仿真优化分析结果基本一致，球面轨迹分布越均匀，加工后的球度误差越小。

6 结束语

为优化轴承球研磨变曲率沟槽结构参数，本文利用数值仿真分析方法，研究了变曲率沟槽几何参数对球面加工轨迹形态、标准差SD和球体运动状态的影响，并得出以下结论：

(1)单因素仿真分析结果显示：随着偏心距和沟槽半角的增加，标准差SD的变化趋势均为先减小后增加，当偏心距为球体直径的2倍、沟槽半角为45°时，标准差SD达到最小值；随着沟槽滚道极径和沟槽间距系数的增加，标准差SD的变化趋势均为先快速减小后变化缓慢，逐渐趋于稳定；

(2)根据各参数水平均值分析，得出最佳几何参数组合：偏心距e/rb=4，沟槽半角α=β=45°，沟槽滚道极径ρ/rb=60，沟槽间距系数s=2；

(3)通过变曲率沟槽几何参数的正交仿真试验，对各参数的显著性进行分析，得出偏心距为显著影响因素，权重39%，沟槽外角β为29%，沟槽内角α为22%，槽间距系数s为9%；

(4)进行了钢球的抛光实验，结果表明，球度误差在最优沟槽结构参数条件下，能够达到最小值，从0.057 μm降低至0.022 μm，与正交试验分析结果基本一致。