电阻应变式称重传感器迟滞性建模及实验研究*
王 靖,高贵军*,寇子明,张 昕,薛政宇
(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.矿山流体控制国家地方联合工程实验室,山西 太原 030024;3.闽江学院 外国语学院,福建 福州 350108)
0 引 言
在采用皮带输送机输送固体散状物料过程中,需要对物料进行连续称重,而电子皮带秤是皮带输送机中对物料进行连续称重的一种计量设备[1]。其中,电阻应变式称重传感器是电子皮带秤系统中最常用的称重传感器,其电阻应变片作为敏感元件可提高电子皮带秤的抗干扰能力和检测灵敏度[2]。
由于电阻应变式称重传感器在称量过程当中出现的迟滞现象,有时称量结果误差会达到5%以上,为了保证电阻应变式称重传感器在称量工作当中的准确性,必须设法减小由于迟滞性带来的称量误差。
起初,为了减小传感器由于迟滞性带来的称量误差,研究人员通过提高传感器精度和增加辅助设备来减小迟滞性(例如:增加传感器数量等),但是成本过高。之后,各国学者提出了通过建立描述迟滞性的数学模型以及曲线拟合等,对迟滞性进行补偿[3]。例如Bouc-Wen模型[4]、Preisach模型[5]、Duhem模型[6]和Prandtle-Ishlinskii模型[7]。其中,Mayergoyz提出的Preisach模型数值实现方法的原理简单、适应范围广、数学表达比较方便,是当前应用最为广泛的迟滞模型[8,9]。但这种离散化数值法不能反映擦除特性,仍然会导致电子皮带秤实际使用过程中出现较大误差[10]。
本研究基于改进前和改进后的Preisach模型[11],对电阻应变式称重传感器的迟滞性进行研究,并给出相关实验验证其正确性,为称重系统当中的迟滞补偿环节提供理论依据。
1 电阻应变式称重传感器工作原理
煤矿厂中,安装在带式输送机上的电子皮带秤将重量信号与速度信号结合起来进行积分运算,即可得出带式输送机上运送煤炭的流量。其中,重量信号通过电阻应变式称重传感器来称量托辊重量所得。
电阻应变式称重传感器主要是由弹性体、电阻应变片和补偿电路组成[12]。弹性体是称重传感器的受力元件,在弹性体受力发生微变形时,电阻应变片也跟着一道变形,使得电阻值发生变化,接连电桥将电阻信号转化为易测量的电压信号。当去掉载荷后,弹性体微应变消失,但大多数情况下,并不能够完全恢复到原始状态,这是造成电阻式应变传感器迟滞性的主要因素。
称重传感器的加载与卸载曲线如图1所示。

图1 加载与卸载曲线
由图1可见,加载过程中的应变曲线ε1与卸载过程中的应变曲线ε2并不重合,其最大差值ε1-ε2=Δε被称为迟滞性,其对称量误差有着较大的影响。
2 Preisach模型的建立
根据经典的Preisach理论,对电阻式应变称重传感器建立的数学模型为:
u(t)=α≥βμ(α,β)γαβ[ω(t)]dαdβ
(1)
式中:u(t)—输出电压信号;μ(α,β)—Preisach模型中的权函数;γαβ[ω(t)]—Preisach模型中的迟滞单元(也称迟滞算子);ω(t)—施加载荷;α—迟滞单元上升阈值;β—迟滞单元下降阈值。
当对电阻应变式称重传感器施加载荷ω(t)后,输出电压u(t)发生相应的变化。由于电阻应变式称重传感器一般只受到压力或者拉力,为单向力,笔者将其定义为正向的值。
而输出电压u(t)也为正向的,所以ω(t)和u(t)只能在第一象限内移动,γαβ[ω(t)]的输出只能为0和1两种,即:

(2)
为便于理解,可通过Preisach模型的几何解释来描述Preisach模型,如图2所示。

图2 Preisach模型的几何解释T—限制点集合(α,β)的三角形;β0—输入空载值;α0—输入满载值;S+—该区域内的迟滞单元值为+1;S0—该区域内的迟滞单元值为0
在图2中,S+和S0的表达式为:
S+={(β,α)∈T|γαβ[ω(t)]=+1}
(3)
S0={(β,α)∈T|γαβ[ω(t)]=0}
(4)
图2(b)中,水平线总是向上移动,表示电压在增大;图2(c)中竖直线总是向左移动,表示电压在减小。当电压增大时,S+区域增大,S0区域减小;当电压减小时,S+区域减小,S0区域增大;图2(c)中,载荷ω(t)的加载方式为β0→α1→β1。
根据Preisach模型,输出电压可表示为:
u(t)=∬S+μ(α,β)γαβ[ω(t)]dαdβ+
∬S0μ(α,β)γαβ[ω(t)]dαdβ
(5)
当(β,α)∈S+时,γαβ[ω(t)]=1;当(β,α)∈S0时,γαβ[ω(t)]=0,所以式(5)可化简为:
u(t)=∬S+μ(α,β)dαdβ
(6)
根据式(6),只要通过对电阻应变式称重传感器进行加载和卸载实验,再对α,β进行两次偏导,就可得到权函数μ(α,β)。而为了避免复杂的偏导计算过程和后续的积分运算,Mayergoyz提出了一种Preisach模型数值实现方法,该方法只需要对输入、输出信号进行加减法运算,即:
u(t)=
(7)

电压加载与卸载过程的几何解释如图3所示。

图3 电压加载与卸载过程的几何解释
图3中,当施加载荷继续变化,按β0→α1→β1→α2→β2→ω(t)过程进行加载,载荷处于增大阶段:当ω(t)<α2时,如图3(a)所示,Preisach模型数值实现方法与经典Preisach模型计算结果一致,积分区间为S+;载荷继续增大,当ω(t)>α2时,如图3(b)所示,Mayergoyz提出的Preisach模型数值实现方法的积分区间会少计算阴影部分,造成计算结果的减小。
同理,假设ω(t)<α1,施加载荷继续变化,按照β0→α1→β1→α2→β2→α3→ω(t)过程进行加载,载荷处于降低阶段:当ω(t)>β2时,如图3(c)所示,Preisach模型数值实现方法与经典Preisach模型计算结果一致,积分区间为S+;载荷继续降低,当ω(t)<β2时,如图3(d)所示,Preisach模型数值实现方法的积分区间会多计算阴影部分,造成计算结果的增大。
通过以上推理发现,当载荷增大到大于上一次上升阶段载荷的极大值,Preisach模型数值实现方法积分区间会减少;当载荷降低到小于上一次降低阶段载荷的极小值时,Preisach模型数值实现方法积分区间会增大,两者都会造成计算结果的误差。
符合Preisach模型数值实现方法的加载过程如图4所示。

图4 符合Preisach模型数值实现方法的加载过程
对电阻应变式称重传感器施加载荷必须符合图4加载过程,方可用Preisach模型数值实现方法计算。而在电阻应变式称重传感器的实际应用当中,载荷的变化过程比较复杂,很有可能不满足Preisach模型数值实现方法的要求。因此,必须对Preisach模型数值实现方法进行改进,使其能适用电阻应变式称重传感器受力载荷的变化要求。
3 Preisach模型数值实现方法的改进
通过图3发现,原模型的计算缺陷在于当ω(t)>α2时,积分区间少计算了阴影部分;当ω(t)<β2时,积分多计算了阴影部分。通过对加载状态的分析,ω(t)>α2是由增加状态载荷大于递减历史极大值造成的,ω(t)<β2是由降低状态载荷小于递增历史极小值造成的。
因此,在Mayergoyz提出的Preisach数值实现方法基础上,笔者通过对加载状态分析来对Preisach数值模型进行改进,改进模型如图5所示。

图5 改进模型
图5(a)为ω(t)>α2改进模型,当增加状态载荷大于递减历史极大值时,增加状态载荷大于递减历史极大值表现为D点值大于B点值,故舍去AB和BC和CD段加载过程,直接从A段加载到D段进行计算;同理,图5(b)为ω(t)<β2改进模型,当降低状态载荷小于递增历史极小值时,降低状态载荷小于递增历史极小值表现为D1点值小于B1点值,舍去A1B1、B1C1和C1D1段加载过程,直接从A1段加载到D1段进行计算。
改进后,Preisach数值模型积分区间如图6所示。

图6 改进后Preisach数值模型积分区间
图6(a)为ω(t)>α2时,将阴影部分也算在积分区间内;图6(b)为ω(t)<β2时,阴影部分不计算在积分区间内,这样则与经典Preisach模型积分区间一致。
改进后,Preisach模型计算流程如图7所示。
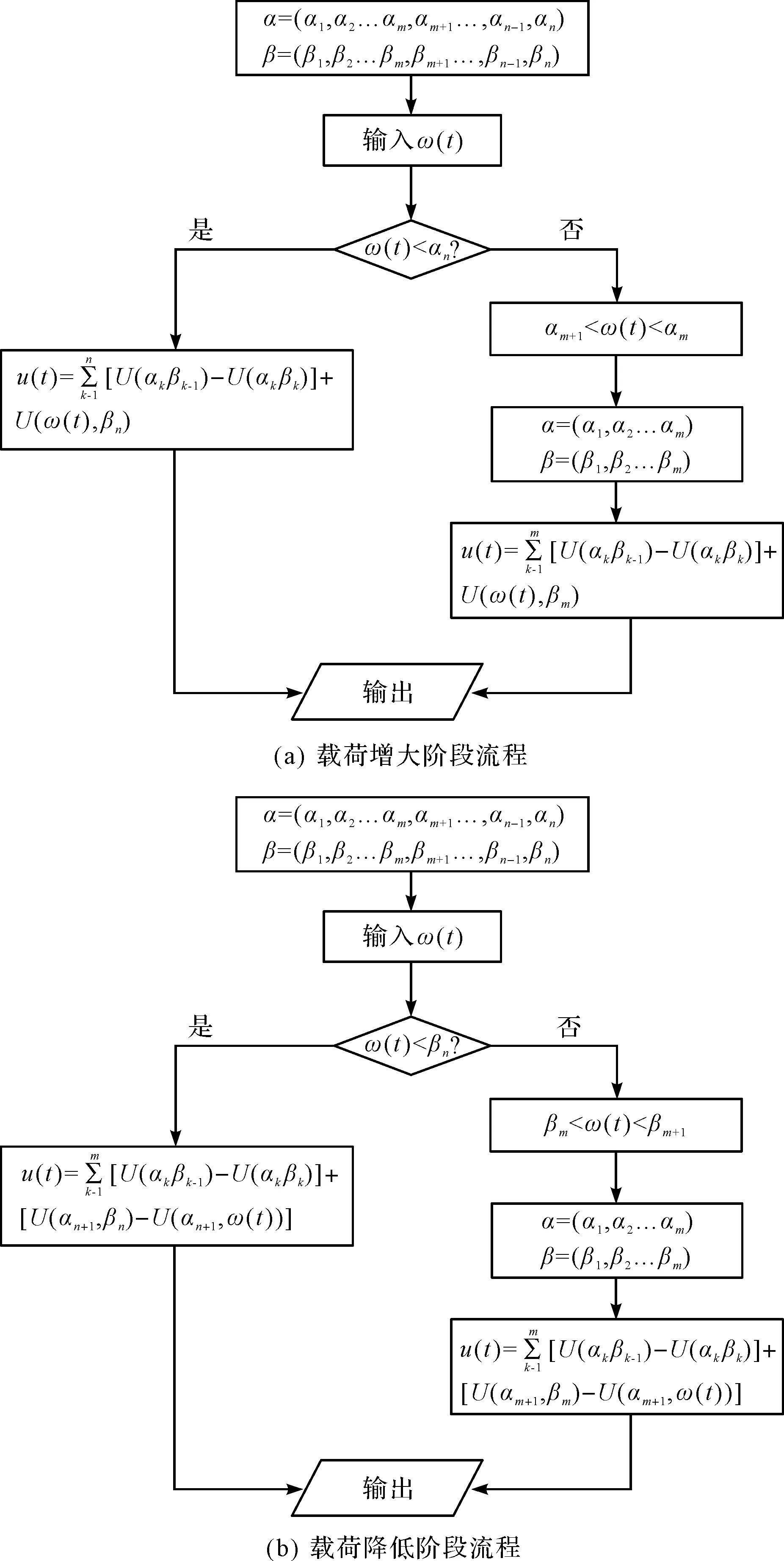
图7 改进后的Preisach模型计算流程
设定数列:α=(α1,α2…αm,αm+1…αn-1,αn);β=(β1,β2…βm,βm+1…βn-1,βn)。其中,1 (1)先判断载荷处于增大状态还是降低状态,当载荷处于增大状态时,继续判断增大状态的载荷是否小于上一次增大状态载荷,如果此次增大状态的载荷小于上一次增大状态载荷,代入设定好的以下公式(8)中,输出结果; (2)如果判断增大状态的载荷大于上一次增大状态载荷,继续判断增大状态的载荷直到其小于之前某次增大状态的载荷αm,保证当前增大状态的载荷处于递减的极大值数列末端,使增大状态载荷计算过程符合图4当中α的加载过程,α的项数由n项缩减到m项,最后将其代入以下公式(8)中; (3)同理,当电阻应变式称重传感器的载荷信号处于降低状态时,判断降低状态的载荷是否大于上一次降低状态载荷,如果此次降低状态的载荷大于上一次降低状态载荷,代入设定好的以下公式(8)中; (4)如果判断降低状态的载荷小于上次降低状态载荷,继续判断降低状态的载荷直到其大于之前某次降低状态的载荷αm,保证当前降低状态的载荷处于递增的极小值数列末端,使降低状态载荷计算过程符合图4当中β的加载过程,β的项数由n项缩减到m项,最后将其代入以下公式中,即: u(t)= (8) 笔者通过实验验证改进后Preisach数值实现方法的有效性,实验平台如图8所示。 图8 实验平台 由于电阻应变式称重传感器的输出电压值比较小,直接测量电压变化情况结果不明显,笔者采用西门子称重模块SIWAREX对电阻应变式称重传感器的输出电压进行放大,将西门子称重模块SIWAREX通过UC232A USB转串口转换器与PC连接,通过PC端SIWATOOLS软件测出称重传感器加载过程当中的输出电压值。 实验1是以每两块铁片为一个单位进行加载、卸载实验。为了减小本次实验对下次实验的影响,需要在每做完一次实验后将电阻应变式称重传感器调到设定的零点,等待5分钟后再做下一次实验。 实验1加载曲线如图9所示。 图9 加载曲线 由图9可知,载荷的加卸载方式具有收敛性。 对应图9进行3次重复实验取平均值,测出加载和卸载过程当中各点电压输出值,如表1所示。 表1 加载过程当中各点电压输出值 通过表1计算得到不同载荷间的电压差值U(α,β),如表2所示。 表2 不同载荷间的电压差值 实验2为增加状态载荷大于递减历史极大值,实验3为降低状态载荷小于递增历史极小值,笔者进行3次重复实验取平均值。 实验2和实验3加载情况时的电压输出对比如表3和表4所示。 表3 实验2加载情况时的电压输出对比 表4 实验3加载情况时的电压输出对比 实验2和实验3中,改进前后Preisach模型数值方法计算结果的误差百分比曲线如图10所示。 图10 误差百分比曲线 由图10可知:通过对比改进前Preisach模型数值方法计算结果与改进后Preisach模型数值方法计算结果的误差曲线,当载荷按照图9所示的收敛趋势加载时,两种模型误差相同,当不符合图9所示的趋势加载时,即增加状态载荷大于递减历史极大值或者降低状态载荷小于递增历史极小值时,改进后的Preisach模型数值方法计算相较于改进前Preisach模型数值方法计算结果误差明显减小,实验中最大误差可由10.26%减小到1.66%,这也验证了前面的理论分析。 而且随着加载次数的增加,当载荷加载顺序不符合图9的收敛加载顺序时,改进后Preisach模型数值方法计算结果会一直比改进前Preisach模型数值方法计算结果误差小,有效减小了误差的累加。 本文对电阻应变式称重传感器的迟滞性进行了分析,在原有的Preisach模型数值方法基础上进行了改进,分别采用改进前和改进后的Preisach模型数值方法对电阻应变式称重传感器的迟滞性进行建模计算;通过重复性实验,发现改进后的Preisach模型数值方法相较于改进前的Preisach模型数值方法更具有适用性;在增加状态载荷大于递减历史极大值或者降低状态载荷小于递增历史极小值的情况下,误差更小。 实验中,最大误差可由10.26%减小到1.66%,而且随着加载次数的增加,有效减少了误差的累加。由此可见,改进后的Preisach模型数值方法可以为电阻应变式称重传感器的迟滞性提供更加准确的数学模型。4 实验及结果分析







4 结束语

