轴承尺寸检测数据的异常值检测与数据处理研究*

何高清，肖 健

(合肥工业大学 机械工程学院，安徽 合肥 230009)

0 引 言

在轴承形廓质量检测中，尺寸检测是重要的检测环节。本文采用多激光传感器并行高速自动化轴承检测设备，在连续尺寸检测过程中，其采样检测点数量众多，检测数据存在异常值与数据波动是不可避免的。正确地识别与处理异常值、降低数据的波动性，对轴承检测结果的准确性与稳定性有重要意义。检测数据发生波动与产生异常值有以下几个主要原因：

(1)由于选用激光传感器进行检测，其检测灵敏度高，外界易对其造成干扰，造成检测数据不稳定；

(2)由于采用类三爪卡盘式固定轴承，当检测到卡盘处时，超出传感器检测量程，会产生异常数据点；

(3)由伺服电机带动卡盘高速旋转，进而对轴承进行检测，高速旋转所带来的振动也会影响检测结果。

异常检测也叫异常挖掘，是指从大量数据中找出其行为明显不同于预期对象的过程[1]。目前，异常数据检测的方法大体可分为基于统计的异常检测方法[2]、基于距离的异常检测方法[3]、基于密度的异常检测方法[4]和基于聚类的异常检测方法[5]等几种。各方法的优缺点分述如下：

(1)基于统计的异常检测方法，通过统计学理论，确定数据的分布模型，分析数据的离散程度和相应模型的评价指标来确定数据的异常程度，这种方法用于分析只包含单种属性的数据；

(2)基于距离的异常检测方法，通过设定距离阈值，计算各数据点与数据集的距离，将大于距离阈值的数据确定为异常数据。该方法不需要数据的具体分布模型，但其算法复杂度较高，不适用于大数据集和密度不均匀的数据集；

(3)基于密度的异常检测方法，能够检测出基于距离异常算法不能识别的一类数据——局部异常，打破了固有的绝对异常的观点，更符合实际应用，但其结果对参数的选择敏感，异常因子阈值的选取需要一定的先验知识；

(4)基于聚类的异常检测方法，一般利用K-Means算法将整个数据集聚类成多个簇，根据假设(异常点不属于任何的簇、异常点一般离最近的簇较远、稀疏簇中的点都被认为是异常的)确定异常数据，但其分类结果依赖于分类中心的初始化，对类别规模差异太明显数据的处理效果不好[6-9]。

本文中检测数据仅关于轴承尺寸属性，而且其数据量大，对系统实时性要求高，因而需要降低检测算法时间复杂度；综合以上异常检测方法的优势与不足并结合轴承尺寸检测数据的分布特点，笔者采用统计学箱型图理论对异常值进行检测，对于异常值用中位数暂代，再利用最小二乘多项式拟合法对原数据异常点处进行校正，且通过该方法对检测数据重新估计，提高检测结果的精度。

1 轴承尺寸检测系统

轴承检测系统主要由硬件系统与软件系统组成，设备实物图如图1所示。

图1 轴承尺寸检测设备

其硬件系统主要包括：激光传感器、光栅尺、HMI触摸屏、伺服驱动器及电机等。

其中，检测系统的硬件：激光传感器选用德国米铱1420型号，检测精度1 μm，完成对轴承的尺寸采样；光栅尺用以记录传感器的位置，并将位置信号送入到DSP中；HMI触摸屏，用以控制整个检测设备，并对不同种类轴承选择相应的测量方案；伺服驱动器及电机，用以将激光传感器移动到检测位置，并带动轴承的旋转运动。

软件系统主要包括DSP(数字信号处理器)，完成对电机的控制、与HMI触摸屏的信息交互、检测参数的处理、检测结果的输出等工作。

轴承产品的合格与否，根据检测结果的最大值、最小值是否在轴承的极限尺寸范围之内判断。

2 异常值的检测与数据处理

2.1 箱型图理论

基于正态分布的3σ准则是以假定数据服从正态分布为前提的，但实际数据往往并不符合正态分布模型，其以均值和方差为基础来判定数据的异常，受异常值本身的影响较大。而箱形图理论无需对数据做出限制，不受异常值的影响，可以直观地描述数据的离散分布情况，并且提供了一个识别异常值的标准，即大于箱型图设定的上界或小于下界的数值即为异常值。

箱型图如图2所示。

图2 箱型图

将检测数据按照从小到大的顺序依次排列X1,X2,…,Xn，得到有序数列，则其中位数M记为：

(1)

异常值的判定标准为：

Xi>U+K·IQR|Xi

(2)

式中：U—上四分位数，区间[M，Xn]的中位数，表明样本中只有1/4的数值大于U；L—下四分位数,区间[X1,M]的中位数，表明样本中只有1/4的数值小于L；IQR—四分位距，IQR=U-L；K—步长系数，取K=1.5。

2.2 中位数暂代

选取中位数暂代异常值，数据集的中位数比平均值具有更强的鲁棒性，理论上可以“容忍”不超过总数据量50%的异常值[10]，并且保证了数据的完整性，有助于对整体数据的最小二乘多项式拟合，即：

Xi=M(Xi>U+K·IQR|Xi

(3)

2.3 最小二乘法多项式拟合

原始检测数据经过异常值检测与替代，继而需要对替换值进行校正。使用最小二乘法多项式拟合的方式，可以根据整体数据的分布趋势对替换值进行校正。同时，利用拟合的方式重新处理数据，降低其波动性。

2.3.1 最小二乘法基本原理

最小二乘法(最小平方法)是一种数学优化技术，通过最小化误差的平方和寻找数据的最佳函数匹配[11]。

对于一组实验数据(xi,yi)(i=0,1,…,m),要求在某个函数类，Φ=span{φ0(x),φ1(x),…,φn(x)}中寻求一个函数，即：

(4)

使φ(x)满足条件：

(5)

由多元函数极值必要条件可知：

(6)

即：

(7)

记：

(8)

则上式可表示为：

α0(φj,φ0)+α1(φj,φ1)+…+αn(φj,φn)=(φj,y)

(9)

写成矩阵形式为：

(10)

式(10)即为最小二乘法求解的法方程组。

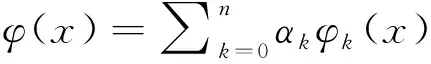
2.3.2 拟合函数的选取

合适的φ(x)可以增强模型对检测数据的解释能力。

以轴承内径尺寸检测为例，本文选用拟合函数为多项式函数，是根据在MATLAB的Curve Fitting工具箱中[12]，利用有理函数、三角函数和多项式函数对筛选和替换后的检测数据拟合后所得到的。

各拟合函数效果如图3所示。

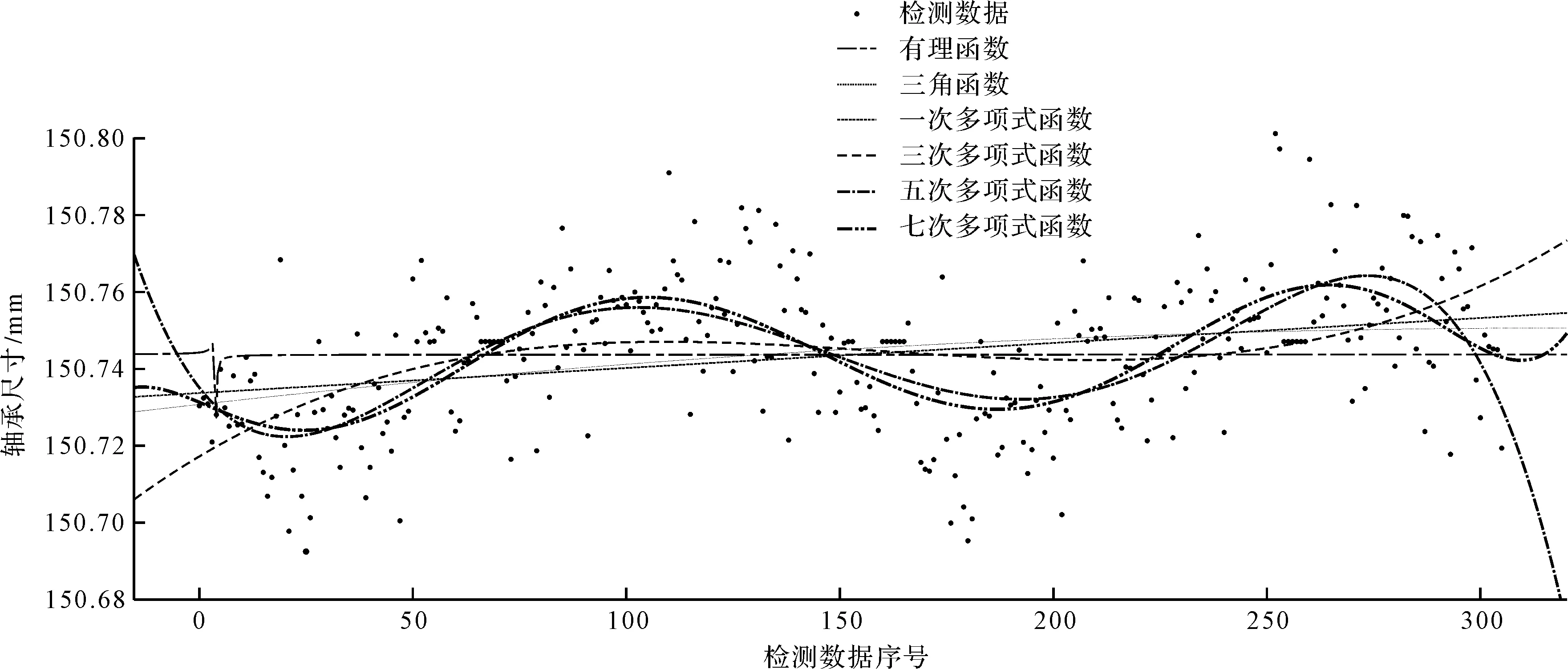
图3 各拟合函数效果

对于曲线拟合效果是否最佳，MATLAB有具体的评价指标SSE和R-square。其中，SSE为误差平方和，该参数计算拟合参数后的回归值与原始数据对应点的误差平方和，SSE越小说明模型选择和拟合得更好；R-square为确定系数，其值越接近1，表明方程的自变量对因变量的解释能力越强，模型对数据的拟合程度越好。

各曲线拟合程度评价指标如表1所示。

表1 各曲线拟合程度评价指标

根据表1中SSE与R-square综合考虑，笔者选择七次多项式函数为拟合函数，即：

φ(x)=α0+α1x+α2x2+α3x3+
α4x4+α5x5+α6x6+α7x7

(11)

3 轴承检测实验及结果分析

笔者以公称内径尺寸为Φ150.7 mm轴承检测为例，进行实验。

检测数据分布与频率分布直方图，如图4所示。

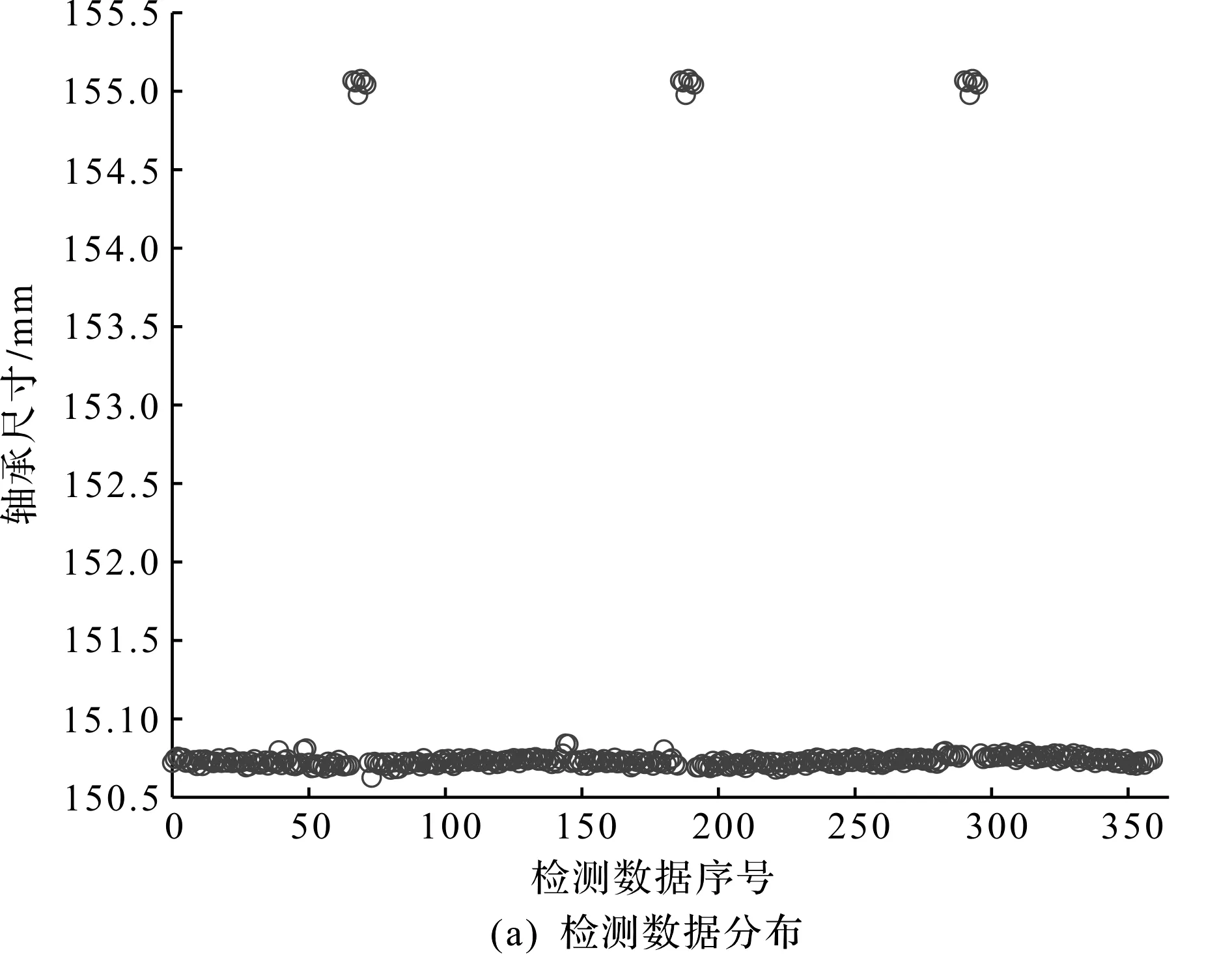
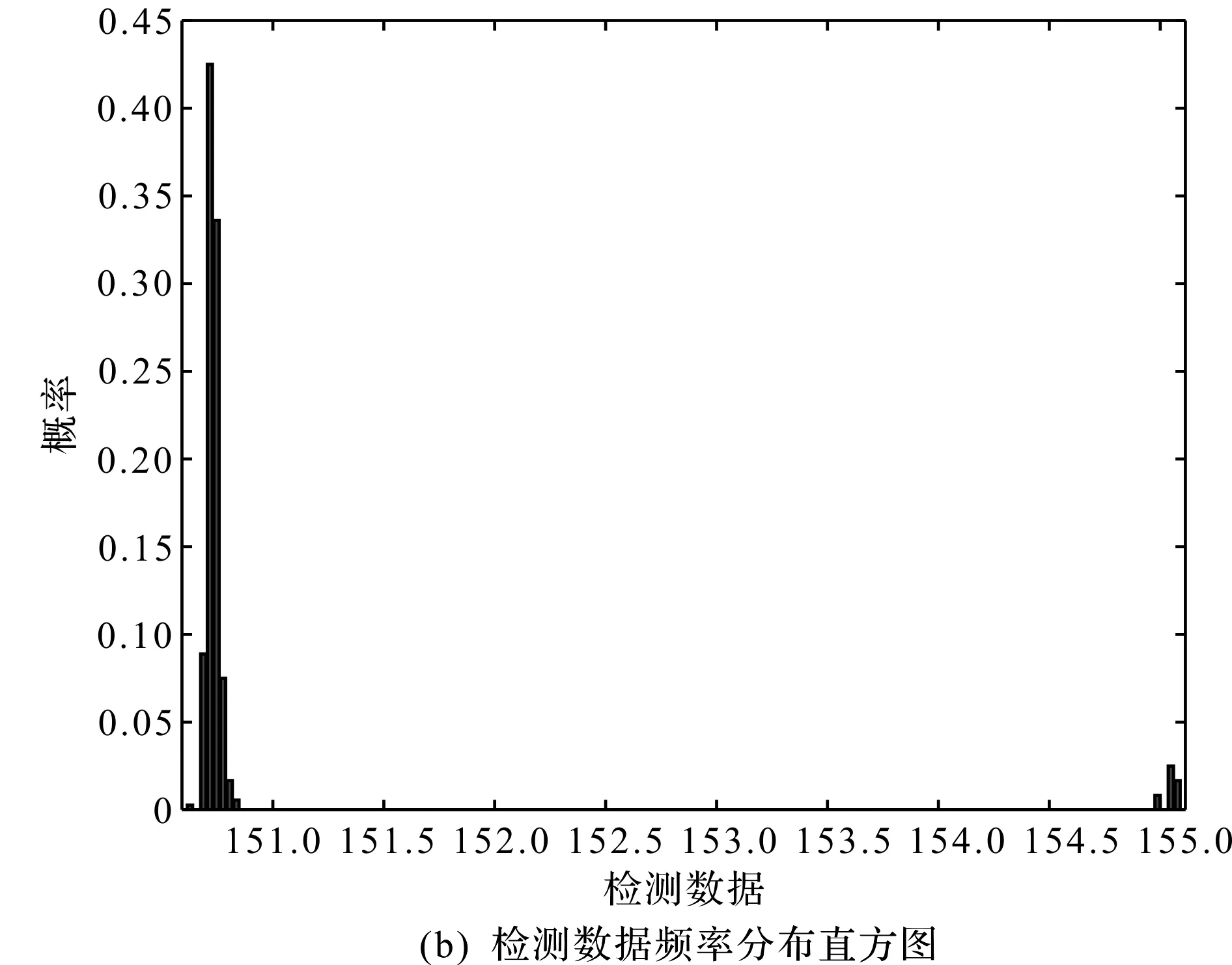
图4 检测数据分布与频率分布直方图

根据图4，通过计算可得到检测数据的均值μ=150.947 0和标准差σ=0.942 2，则正态分布的概率密度曲线f(x)为：

(12)

检测数据箱型图和概率密度曲线f(x)如图5所示。

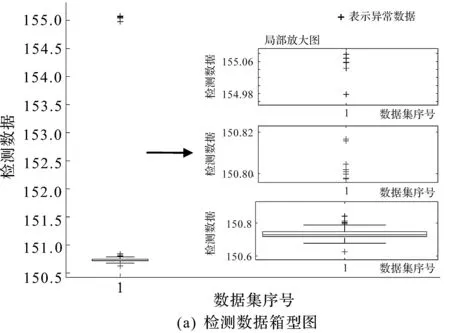
图5 检测数据箱型图和概率密度曲线f(x)

当传感器检测到卡盘处时，会得到如图4(a)中的上部异常数据。由图5(a)观察可知，箱型图可以检测出这类异常数据以及其他原因所造成的异常值。由图4(b)与图5(b)对比可知，检测数据的实际分布模型不符合正态分布。

笔者分别使用箱型图法与3σ准则法识别数据的异常值，异常数据检测结果如表2所示。

表2 异常数据检测结果

由表2结果对比可知：箱型图法的异常值识别率高于3σ准则法2.3%，而且箱型图法的异常值识别区间小于3σ准则法，表明箱型图法对异常值的识别准确率更高；主要由于3σ准则法要求数据服从正态分布，然而实际数据分布并不能满足要求。

因此，在大数据量的检测系统中，箱型图法更具有优势，故在本研究中选用箱型法作为检测异常值的方法。

笔者分别用检测数据的中位值与平均值替换异常值。异常值替换后数据分布如图6所示。

图6 异常值替换后数据分布

由图6可知：用中位值替代异常值数据分布更为集中化，均值由于受异常值影响较大，而且其在箱型图法中属于异常值，不适合选作替换值。

综上所述，笔者认为选取中位数更为合适。

笔者对用中位数替换后的数据进行拟合。七阶多项式最小二乘拟合结果如图7所示。

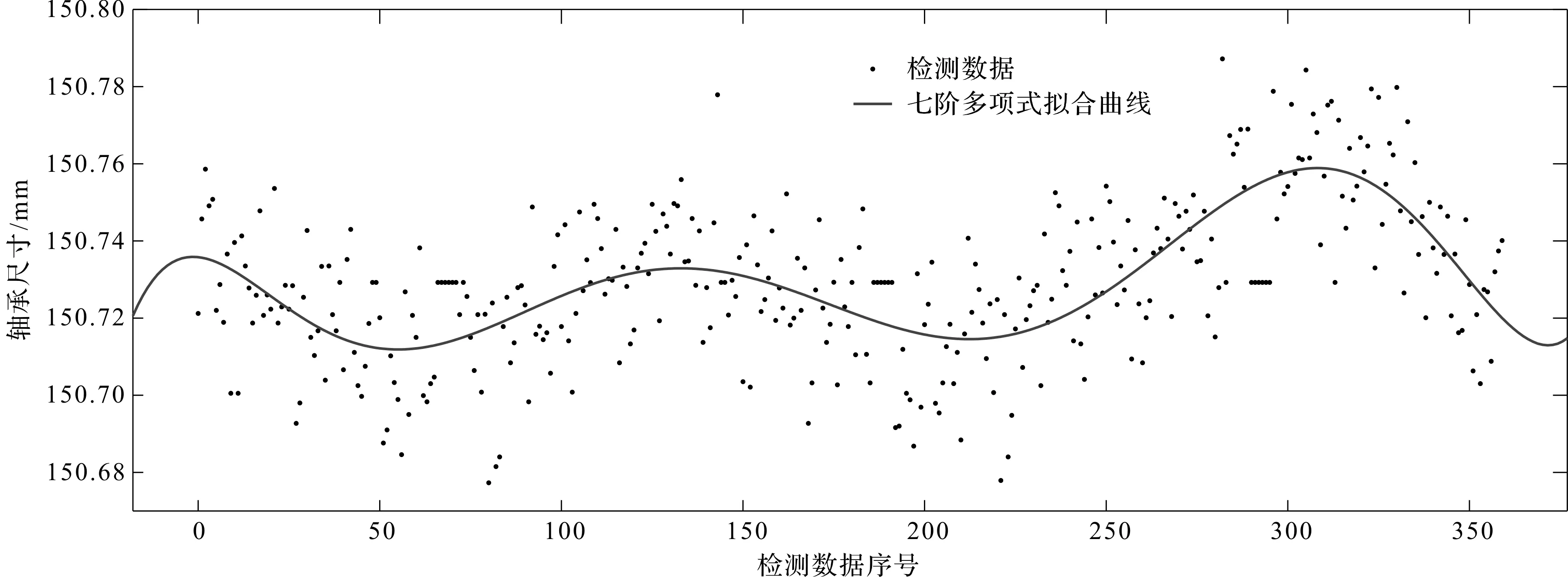
图7 七阶多项式最小二乘拟合

由图7可知，未经拟合时数据的波动范围约为0.1 mm，七阶多项式拟合后数据的波动范围约为0.05 mm，明显地降低了数据的波动性；拟合的数据分布相比较直接用中位值替代的数据分布，更符合实际测量趋势。

4 结束语

针对轴承检测系统中出现的异常值与数据波动问题，笔者采用统计学箱型图理论对异常值进行检测，对于异常值用中位数暂代，再利用最小二乘多项式拟合法对原数据异常点处进行校正，且通过该方法对检测数据重新估计。

实验及研究结果表明：

(1)箱型图法异常值识别率高于3σ准则法2.3%，可准确、快速地识别异常值；

(2)中位值替换的方式受异常值影响较低，保证了检测数据的完整性；

(3)通过最小二乘多项式拟合的方式，数据波动降低为原来的50%，使数据分布更为合理化。

此方法的时间和空间复杂度低，易于实现编程，可保证检测系统的实时性和准确性。因此，对于使用位移传感器测量零件尺寸的系统具有一定的参考价值。